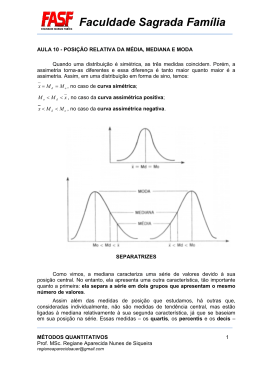
Técnicas de descrição Gráfica
• Tabelas: quadro resumindo o nosso conjunto de observações.
• Toda tabela deve conter: Título, Cabeçalho, Células e Fonte
Altura média dos estudantes do Ensino Médio de Japaraíbe
Escola
Altura (m)
A
1,65
B
1,71
C
1,63
D
1,67
E
1,70
F
1,69
Média Geral
1,675
Fonte: Censo Escolar do Município de Japaraíbe, 2006
Título
Cabeçalho
Células
Fonte
Técnicas de descrição Gráfica
• Gráficos
Regiões Geográficas do
Brasil
Altura (m)
F
1.69
E
Sudoeste
11%
Sul
7%
1.7
D
Norte
45%
1.67
C
Nordeste
18%
1.63
B
1.71
A
1.65
CentroOeste
19%
Altura (m)
1.72
Altura (m)
1.7
1.68
1.75
1.66
1.7
1.64
1.65
1.62
1.6
1.6
1.58
1.55
A
B
C
D
E
F
A
B
C
D
E
F
Técnicas de descrição Gráfica
• Cartogramas
Técnicas de descrição Gráfica
• Pictogramas
Distribuição de Frequência
Tabela - Número de irmãos de alunos do curso de Estatística
Número de irmãos
Frequência
Frequência Relativa
Frequência Acumulada
0
1
2
3
4
Total
1
4
6
3
1
15
0.067
0.267
0.4
0.2
0.067
1
1
5
11
14
15
15
Frequência simples: número de vezes que um valor foi observado.
Frequência relativa: razão entre frequência simples e frequência total
Frequência acumulada: total das frequências de todos os valores inferiores ao
limite superior de uma dada classe
Representações Gráficas
• Histogramas e Polígonos de frequência
Medidas Separatrizes - Quartis
• Os quartis dividem o conjunto de valores em
quatro subconjuntos de mesmo número de
elementos
Estatística Notação
1o Quartil
Q1
2o Quartil Q2 = Md
3o Quartil
Q3
Interpretação
25% dos dados são menores ou iguais ao do 1o
Quartil
50% dos dados são menores ou iguais ao do 2o
Quartil
75% dos dados são menores ou iguais ao do 3o
Quartil
Posição
p = 0,25 (n + 1)
p = 0,50 (n + 1)
p = 0,75 (n + 1)
Medidas Separatrizes - Percentis
• São os noventa e nove valores que dividem uma série de
dados em 100 partes com o mesmo número de elementos.
• Indicamos o 1º percentil como P1, o 2º como P2 e assim por
diante.
• É importante notar que P25 = Q1, P50 = Md e P75 = Q3
Estatística
Notação
Interpretação
Posição
5o Percentil
P5
5% dos dados são menores ou
iguais ao do 5o Percentil
p = 0,05 (n + 1)
50o Percentil
P50 = Q2 = Md
50% dos dados são menores ou
iguais ao do 50o Percentil
p = 0,50 (n + 1)
95o Percentil
P95
95% dos dados são menores ou
iguais ao do 95o Percentil
p = 0,95 (n + 1)
Medidas de Dispersão
• Variância
– média aritmética dos quadrados dos desvios
Medidas de Dispersão
• Desvio Padrão
– Raiz quadrada da variância
– Propriedades:
• Se somarmos ou subtrairmos uma constante de todos os
valores da série, o desvio padrão não se altera.
• Se multiplicarmos ou dividirmos uma constante por todos os
valores da série, o desvio padrão será multiplicado ou divido
por esta mesma constante.
Noções de Assimetria
• Se x = Md = Mo, a curva é simétrica
• Se Mo < Md < x, a curva é assimétrica
positiva.
• Se x < Md < Mo, a curva é assimétrica
negativa.