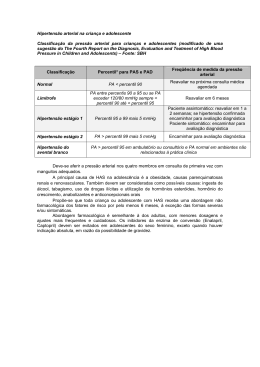
Análise de Correspondência em acessos de pimenta
Bruno Caetano Vidigal1
Paulo Roberto Cecon2
.
1 Introdução
A Análise de Correspondência (AC) é uma das diversas técnicas de análise multivariada
desenvolvida para o estudo da relação entre variáveis qualitativas em tabelas de contingência
(BEH, 2004). Ela permite a visualização gráfica das linhas e colunas como pontos em espaços
vetoriais de dimensões reduzidas em um novo sistema de eixos ortogonais.
A AC tem se tornado muito comum devido a sua fácil implementação. Necessita apenas
de uma tabela com números positivos que representam freqüências observadas de objetos ou
indivíduos classificados por uma categoria de linha e uma categoria de coluna; tais categorias
devem ser mutuamente exclusivas e exaustivas, ou seja, um indivíduo ou objeto não pode ser
classificado em mais de uma categoria de uma mesma variável e devem existir categorias
suficientes para esse ser classificado (GREENACRE, 2007).
Esse trabalho teve o objetivo de avaliar as similaridades e dissimilaridades das variáveis
observadas em acessos de pimenta a partir do mapa de ACM.
2 Material e Métodos
Foram avaliados 49 acessos de C. chinense pertencentes ao Banco de Germoplasma de
Hortaliças da Universidade Federal de Viçosa (UFV), quanto a características quantitativas e
qualitativas dos frutos das plantas.
O experimento foi conduzido no delineamento de blocos ao acaso, com três repetições,
utilizando espaçamento de 1m x 1m entre plantas e linhas, sendo cada linha representada por
três plantas de cada acesso.
O quadro abaixo mostra as variáveis pertencentes ao estudo.
Quadro 1 – Variáveis em estudo
Variável
Label
1
DET - UFV. e-mail: [email protected]
DET - UFV. e-mail: [email protected]
Agradecimento à FAPEMIG e à CAPES pelo apoio financeiro.
2
1
Tipo da variável
CF (mm)
Comprimento
Contínua
LF (mm)
Largura
Contínua
PMS100
Porcentagem de matéria seca
Contínua
Massa (g)
Peso
Contínua
EP (mm)
Expessura do mesocarpo
Contínua
TSS
Teor de sólidos solúveis
Contínua
CFM
Cor do fruto maduro
Categórica nominal
PF
Ponta do fruto
Categórica nominal
Utilizamos o método dos percentis para categorizar as variáveis. Veja o quadro abaixo.
Quadro 2 – Categorização das variáveis pelo método dos percentis
Categoria 1
Valores menores ou iguais ao percentil 20
Categoria 2 Valores maiores que o percentil 20 e menores que ou iguais ao percentil 40
Categoria 3 Valores maiores que o percentil 40 e menores que ou iguais ao percentil 60
Categoria 4 Valores maiores que o percentil 60 e menores que ou iguais ao percentil 80
Categoria 5
Valores maiores que o percentil 80
2.1 Análise de Correspondência Múltipla
A Análise de Correspondência (AC) teve sua origem atribuída a trabalhos
desenvolvidos por Karl Pearson, com destaque para a estatística Qui-Quadrado, que permite
avaliar se as variáveis dispostas numa tabela bidimensional se afastam do pressuposto de
independência a ponto de fornecer evidência estatística suficiente para indicar associação.
O objetivo da AC é encontrar o subespaço ótimo de menor dimensão que melhor se
ajusta aos pontos da nuvem. (BENZÉCRI, 1992) Daí, esse subespaço ótimo é formado pelos
eixos fatoriais que passam pelo centro de gravidade e que minimizam as distâncias dos pontos
até ele. Primeiramente encontra-se um eixo que passa pelo centro de gravidade e que
minimiza a distância perpendicular dos pontos a reta (primeira dimensão). Logo após, traça-se
uma segunda reta ortogonal a primeira que também passa pelo centro de gravidade que
minimize as distâncias dos pontos em relação a esta reta. Esse processo ocorrerá até se
encontrar min (I-1, J-1) dimensões.
2
Uma forma de se obter as coordenadas dos perfis de linha e coluna no novo sistema de
eixo fatorial é através da decomposição do valor singular da matriz A  UDV T onde U
contém os vetores singulares a esquerda de A, V os valores singulares a direita de A e D é
uma matriz diagonal de números positivos, valores singulares, em ordem decrescente.
Dessa forma as coordenadas principais dos perfis de linha e coluna são dadas por
F  Dr1/ 2UD e G  Dc1 / 2VD , respectivamente, onde Dr é a matriz diagonal do perfil da
coluna marginal e Dc é a matriz diagonal do perfil da linha marginal.
Assim como a AC, a Análise de Correspondência Múltipla (ACM) é também uma
técnica de análise exploratória de dados, só que aplicada a tabelas multidimensionais.
Existem duas maneiras de se aplicar a ACM. Uma delas é a partir da matriz
indicadora, onde as linhas correspondem a cada indivíduo ou objeto de análise e as colunas
são as variáveis com suas categorias. Essa matriz possui os elementos na forma de variáveis
dummy, ou seja, quando for 1, o objeto i é classificado na categoria j da variável q, e 0, caso
contrário. O objeto i só pode pertencer a uma categoria para cada variável. A outra possível
abordagem da ACM é utilizando a matriz de Burt, uma matriz simétrica que contém todos os
cruzamentos possíveis 2x2 entre as Q variáveis envolvidas, sendo que a diagonal principal é
formada de matrizes diagonais de freqüências marginais de coluna.
A matriz de Burt é calculada a partir do produto da transposta da matriz indicadora por
ela mesma. Uma vantagem do uso da matriz de Burt é reduzir o problema de células vazias
quando se tem muitas categorias e variáveis, justamente pelo fato desta trabalhar com
freqüências marginais.
Esse estudo foi realizado apenas com a análise da matriz de Burt.
3 Resultados e Discussões
Como comentado posteriormente, o interesse era estudar as similaridades e
dissimilaridades das variáveis que foram mensuradas no experimento em blocos ao acaso.
Assim, a ACM permite essa visualização através do mapa de correspondência. A seguir,
encontra-se o mapa.
3
Figura 1 – Mapa de Correspondência em acessos de pimenta
Observa-se que 30,7% de toda a inércia (variação) é explicada pela primeira dimensão,
ao passo que a segunda dimensão explica apenas 11,4%. Não será apresentado os mapas
referentes às demais dimensões já que elas não carregam informações adicionais.
É válido considerar que a solução apresentada é da matriz de Burt e não da matriz
indicadora, com dimensões de 40x40. Assim, o resultado apresenta 32 dimensões, pois
existem 40 categorias de 8 variáveis, e o total de soluções é a subtração do número de
variáveis do número de categorias.
A partir da figura 1, observa-se que os maiores níveis de largura do fruto(LF_4 e
LF_5), comprimento (CF_4 e CF_5), espessura do mesocarpo (EP_4 e EP_5) e massa (Ms_4
e Ms_5), estão associados a menor porcentagem de matéria seca (PMS100_1 e PMS100_2) e
teor de sólido solúvel (TSS_1 e TSS_2) e também com as pontas de fruto do tipo 3 e 4 (PF_3
e PF_4).
Sobre a cor dos acessos de pimenta, tem-se que vermelho (CFM_2) e verde-roxo
(CFM_4) são as que mais se relacionam com os níveis das categorias analisadas acima. Isso
pode ser explicado pela maior freqüência de acessos dessas duas cores na base de dados.
4
A cor roxa (CFM_6), que está no quadrante inferior a esquerda, isolada das demais, pode ter
esse comportamento explicado pela sua baixa freqüência.
4 Conclusões
Conclui-se que a dimensão 1 do gráfico de ACM conseguiu separar no quadrante do
lado direito os maiores níveis das variáveis espessura do mesocarpo, largura do fruto e massa
com os menores níveis de porcentagem de matéria seca e teor de sólido solúvel. Assim, no
lado esquerdo do mapa, encontra-se os demais níveis dessas variáveis.
É válido lembrar também que tanto a categorização das variáveis a partir dos percentis
quanto a ACM foram eficientes, de modo que o resultado gráfico foi bastante coerente.
Referências
BEH, E.J. Simple Correspondence analysis: a bibliographic review. International
Statistical. Review, v.72,n.2, p 257-284, 2004.
BENZÉCRI, J.P. Correspondence Analysis Handbook. New York: Marcel Dekker,1992.
GREENACRE,M. Correspondence Analysis in Practice, second edition: Boca Raton:
Chapman & Hall/CRC, 2007.
R Development Core Team. R: A language and environment for statistical computing, 2.13. R
Foundation for Statistical Computing: Vienna, 2011. Disponível em http://www.Rproject.org.
5