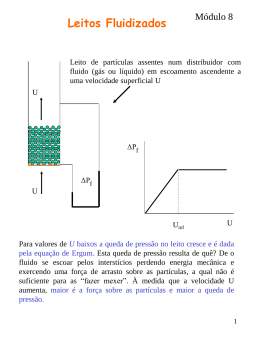
Módulo 7
Fluxo através de meios porosos
O caso de as partículas não serem
esferas define-se um diâmetro
equivalente:
d ep  3 6V
π
Empilhamento
que é o diâmetro de uma
esfera com o mesmo
volume da partícula
Grelha
A porosidade do leito, e,
representa a fracção do
leito não ocupada por
partículas
Fluido (líquido ou gás)
e  volume de "poros"
volume total
A área específica de uma partícula
S p  área externa de uma partícula
volumeda partícula
A área específica do leito de partículas
S  S p (1  ε)  área externa das partículas
volume do leito
1
Se o tubo que contém o leito for cilíndrico, a área da secção
recta é A= pD2/4. Se se fizer um corte por um plano que
contém a secção recta observa-se:
Ap  A 1  e 
Alivre  A e
área da sec ção recta ocupada por partículas
área da sec ção recta livre para a passagem de fluido
Quando um caudal volumétrico Q de fluido escoa num meio
poroso contido num tubo de secção recta A, a velocidade
superficial U do fluido é dada por
U Q
A
Como nem toda a área da secção recta está livre para o
escoamento do fluido define-se a velocidade média
intersticial
U
u Q 
Ae e
2
Perda de carga num escoamento através de um leito
poroso
Equação de Karman-Kozeny- regime laminar
Imagine-se que o fluido percorre os interstícios como se
estes fossem capilares. A perda de carga neste caso será dada
pela equação de Poiseuille para escoamento em tubos
Se o percurso fosse a “direito” a
velocidade seria a intersticial e o
percurso o comprimento do leito
L
u
No entanto o percurso é sinuoso, o
comprimento equivalente percorrido
pelo fluido é maior que o percurso a
direito, consequentemente, para um
igual tempo de permanência do fluido,
a velocidade equivalente é maior
L  Le  u  u Le  U   tortusidade 
e
u ue
L e
3
Equação de Poiseuille num tubo
cilíndrico
P  32 μ2u L
D
Equação de Poiseuille
conduta não circular
numa

P  k μ 2u L
Dh
Com o diâmetro hidráulico definido por
Dh 
4  área de fluxo
 4  volum ede fluido  4  e A L
perím etrom olhado
área m olhada
S AL
u  ue 
U
e
 4e
S

L  Le
 S2 U
k
P  k  μ
 μ 2  Le
2 16
 4e 
e e


 S 


ue Le
Equação de Karman-Kozeny
k 2 S 2
S2
P   μ 3 UL  k μ 3 UL
16
e
e
4
Para um leito de esferas k é aproximadamente igual a 4,2
pd
S p  área externa de uma partícula  p p  6
volume da partícula
d 3p d p
6
2
S  S p (1  ε)  área externa das partículas 
volume do leito
6
dp
(1  ε)
A equação de Karman-Kozeny (regime de escoamento laminar)
para partículas esféricas toma a seguinte forma:
P  150
1 e 2
e3
μUL
d p2
Equação de Burke- Plummer - regime turbulento
Em regime turbulento num tubo horizontal cilíndrico
1
2
P  C f
L
 u2
D
(C f factor de Fanning)
5
Num leito poroso
Dh 
4  área de fluxo
 4  volum ede fluido  4  e A L
perím etrom olhado
área m olhada
S AL
 4e
S
L  Le
L  Le  u  u Le  U   tortusidade 
e
u ue
L e
Substituindo
2
Le
U 
1


P  C f
  2
2
4e / S  e 
Equação de Burke-Plummer
C
S
S
P  f  3 3  L U 2  k  3  L U 2
8
e
e
Para um leito de esferas
S
6
dp
(1  ε)

1 e 
U2
P  k
L
e3
dp
6
Note-se que no coeficiente de atrito devem estar
contabilizadas as perdas de carga nas mudanças bruscas de
direcção (equivalentes a perdas localizadas nos cotovelos)
que são uma parcela importante, em regime turbulento, das
perdas totais no escoamento.
O valor de k para leitos de esferas foi determinado
experimentalmente e é 1,75
1 e
U2
P  1,75 3  L
dp
e
Equação de Ergum para regimes laminar-transiçãoturbulento
Ergum verificou experimentalmente que a adição das
equações de Karman-Kozeny e Burke-Plummer satisfaz
razoavelmente os dados obtidos em toda a gama de condições.
P
L

1 e 2
 150
μ
e3
U
1 e U 2
 1,75 3 
2
dp
e
dp
7