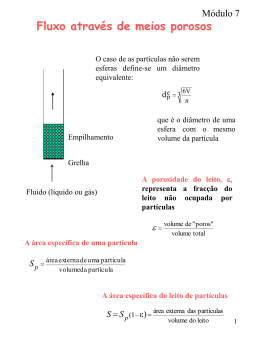
UNIVERSIDADE DO PORTO
FACULDADE DE ENGENHARIA
DEPARTAMENTO DE ENGENHARIA MECÂNICA E GESTÃO INDUSTRIAL
Maria Paula Moreira de Carvalho Amorim Neto Pimenta
TRANSFERÊNCIA DE CALOR ACIMA DA SUPERFÍCIE LIVRE DE UM
LEITO FLUIDIZADO BORBULHANTE
Dissertação apresentada à Faculdade de Engenharia da Universidade do Porto para
obtenção do grau de Doutor em Ciências de Engenharia
ORIENTADOR
Carlos Manuel Coutinho Tavares de Pinho
Professor Associado da Faculdade de Engenharia da Universidade do Porto
CO-ORIENTADOR
Albina Maria de Sá Ribeiro
Equiparada a Professor Coordenador do Instituto Superior de Engenharia do Instituto
Politécnico do Porto
Trabalho financiado por PRODEP III e FCT
Porto, Julho de 2007
Ao Francisco,
ao Zé,
ao Miguel.
Resumo
O objectivo fundamental deste trabalho consistiu no estudo da transferência de calor na
zona imediatamente acima da superfície livre de um leito fluidizado borbulhante para uma
parede de membrana que confinava o reactor. Existiam poucos dados na literatura técnica e
científica sobre fenómenos de transferência de calor nesta região e as informações disponíveis
resumiam-se a estudos de transferência de calor para feixes de tubos colocados na referida
região do reactor, ao passo que informações sobre transferência de calor para paredes de
membrana eram escassas. Como nos leitos à escala industrial a região imediatamente acima
do leito está confinada por paredes de membrana, achou-se conveniente tentar quantificar os
valores da transferência de calor nestas circunstâncias, assim como identificar os principais
mecanismos envolvidos no fenómeno. Determinou-se ainda a influência da mecânica de
fluidos do leito e constatou-se que o borbulhamento, e subsequente projecção e espalhamento
das partículas têm um peso fundamental na definição da transferência de calor.
Este estudo foi importante uma vez que os leitos fluidizados são uma tecnologia de
queima relativamente recente que tem dado boas provas em termos de controlo de emissões
de poluentes gasosos, e ao mesmo tempo se tem revelado bastante adequada à queima de
biomassa, uma das fontes renováveis de energia que poderá ser relevante no futuro
combinado energético nacional e europeu.
Pretendeu-se então caracterizar os mecanismos de transferência de calor envolvidos
entre o leito e as superfícies de contacto imediatamente acima deste, comparando a sua
importância relativa face às diferentes condições de operação. Para isso foi construída uma
instalação de leito fluidizado à escala laboratorial, constituída por um reactor aquecido por
uma resistência eléctrica de 2 kW, seguido de um permutador com uma parede de camisa por
onde circulou água, tecnicamente designada por parede de membrana. A experiência foi
realizada a quente sendo avaliadas as temperaturas do lado da água e do lado dos gases, bem
como a variação da pressão no interior do leito e acima deste ao longo da zona de transporte
das partículas de menor dimensão. Para constituição do leito usou-se areia de sílica de cinco
granulometrias diferentes, e a fluidização foi conseguida com gás. Numa primeira fase o
estudo foi feito só com ar à pressão atmosférica e usando temperaturas entre 400 e 700 ºC.
I
Numa segunda fase usou-se ar e propano comercial, provocando-se a combustão no interior
do próprio leito, devido à auto-ignição do propano face à temperatura imposta.
Com os dados recolhidos, tendo em atenção as diferentes condições de operação,
desenvolveram-se várias correlações gerais para quantificar o coeficiente global de
transferência de calor entre o leito e a superfície de membrana. Foi também estudada a
importância do tamanho das partículas na taxa de transferência de calor e desenvolvidas
correlações em termos de um coeficiente de convecção das partículas. Além disso procurou-se
quantificar a taxa de arrasto das partículas a partir da superfície do leito, tendo por base a sua
importância na transferência de calor.
Como todo o trabalho inovador a nível experimental, que pretende esclarecer temas
ainda pouco desenvolvidos, neste também surgiram algumas limitações físicas inerentes à
própria instalação experimental e que só foram sendo detectadas no decorrer do próprio
processo. Uma delas foi a baixa potência térmica no aquecimento do leito que não permitiu
alargar a gama de trabalho no que diz respeito aos caudais de gás usados; outra limitação foi a
incapacidade de visualização quer do escoamento do leito quer da progressão da chama
decorrente da reacção de combustão do propano. Aumentar a potência de aquecimento era no
entanto arriscado face às dimensões da própria instalação e a visualização pretendida é
complicada face à necessidade de usar materiais que resistam às altas temperaturas reinantes
nos ensaios de combustão.
II
Abstract
The main objective of this work was the study, in the free board of a bubbling
fluidized bed, of the heat transfer towards a water cooled confining membrane wall. The
available data in the technical and scientific literature, concerning the heat transfer in this
region, is scarce and concerns essentially heat transfer across tube bundles placed in the free
board region, while data on the heat transfer towards membrane walls is almost non-existent.
In prototype and industrial fluidized bed plants, the free board confining walls are
mainly of the membrane type and, accordingly, it was considered relevant to look at happens
in this region in terms of heat transfer mechanisms and to find out the influence of the fluid
mechanics of the fluidized bed upon such heat transfer mechanisms. It was found that particle
projection and splashing had a relevant impact upon the heat transfer rate.
The present study is important because fluidized beds are a relatively new burning
technology and are being extensively used for biomass combustion, a renewable energy
source which is expected to have a relevant role in the future national and european energy
mix scenarios.
To perform these experiments, to characterize the heat transfer mechanisms in the
freeboard region of a bubbling fluidized bed, a laboratory scale fluidized bed reactor, heated
by a 2 kW electric resistance, was built. The bed had water cooled membrane walls in the
freeboard region. High temperature tests were done with temperature and pressure drop
readings in the bubbling bed, freeboard and circulating region, and in the cooling water flow.
The bed was composed by silica sand and fluidized with air in the 400-700 ºC temperature
range and with air propane combustion gases above 700 ºC. Five different sand particle sizes
were tested.
Through the measured data, several correlations were developed to quantify the global
heat transfer coefficient under different operating conditions. The importance of particle size
on the heat transfer rate was also studied and, again, a correlation for the particle heat transfer
coefficient is presented. The particles transportation rate away from the bed surface was
quantified, based on the fraction of the global heat transfer that was assigned to the energy
transportation out of the bed by the particles.
III
As expected in any new experimental work, some set backs occurred which were
dependent upon the physical limitations of the experimental layout. Such was the case of the
small amount of bed heating power which limited the fluidizing gas flow operating rate;
another limitation was the lack of visualization capabilities during the progression of the
experiments. However, due to the small reactor size the increase of heating power has some
limitations and the installation of visualization ports is a complicated matter because of high
temperature materials required for the combustion experiments.
IV
Résumé
Le principal objectif de ce travail a été l’étude du transfert de chaleur dans la zone
immédiatement au-dessus de la surface libre d’un lit fluidisé bouillonnant vers une paroimembrane aqueuse qui confinait le réacteur. Dans la littérature technique et scientifique il y
avait peux de données sur des phénomènes de transfert de chaleur dans cette région et les
informations disponibles se rapportent à des études de transfert de chaleur vers des faisceaux
tubulaires mis sur la susdite région du réacteur, tandis que des renseignements sur la transfert
de chaleur vers des parois-membranes étaient insuffisants. Comme dans les lits à l’échelle
industrielle la région immédiatement au-dessus du lit est limitée par des parois-membranes,
on a trouvé convenable d’essayer de quantifier les valeurs de transfert de chaleur dans des
circonstances pareilles, aussi bien que d’identifier des principaux mécanismes rapportant le
phénomène. On a encore déterminée l’influence de la mécanique des fluides du lit et on a
constaté que le bouillonnement et la conséquente projection et éparpillement des particules
ont un poids très important dans la définition du transfert de chaleur.
Cet étude a été important parce que les lits fluidisés sont une technologie de brûlage
relativement récente qui a fait de bonnes preuves en ce qui concerne le controle d’émissions
de polluants gazeux et, en même temps, il est assez utilisé d’une forme acceptable pour la
combustion de la biomasse, une des sources renouvelables d’énergie qui pourra devenir
importante dans un futur national et européen.
On a décidé de caractériser les mécanismes de transfert de chaleur qui se déroulaient
entre le lit et les surfaces de contact immédiatement au-dessus de celui-ci, comparant leur
importance relative face aux différentes conditions d’opération. Pour réaliser cette expérience
on a construit une installation de lit fluidisé à l’échelle de laboratoire, constituée par un
réacteur chauffé par une résistance électrique de 2 kW, suivi d’un échangeur à paroimembrane refroidie à l’aide d’eau. L’expérience a été faite à chaud, en évaluant les
températures, soit de l’eau, soit des gaz, ainsi que la variation de la pression à l’intérieur du lit
et au-dessus de celui-ci tout au long de la zone de transport des particules de dimensions plus
petites. On a utilisé du sable de silice de cinq différentes granulométries et la fluidisation a été
réussie à travers ce gaz. Premièrement l’étude a été seulement faite avec de l’air à la pression
atmosphérique utilisant des températures entre 400 et 700ºC. Deuxièmement on a utilisé de
V
l’air et du propane commercial provocant la combustion à l’intérieur du lit lui-même dû à
l’auto ignition du gaz propane face à la température imposée.
Avec les résultats obtenus, considérant les différentes conditions d’opération, plusieurs
corrélations générales furent développées pour quantifier le coefficient global de transfert de
chaleur entre le lit et la surface de la membrane. L’importance de la dimension des particules
dans le taux de transfert de chaleur a été étudiée et des corrélations concernant le coefficient
de convection des particules ont été développées. En outre, on a cherché à quantifier le taux
de transport des particules à partir de la surface du lit ayant par base son importance dans le
transfert de chaleur.
Comme en tout travail innovateur de niveau expérimental qui vise éclaircir des thèmes
encore peu développés, quelques limitations physiques inhérentes à l’installation
expérimentale elle-même ont surgi e celles-ci n’ont pas été détectées qu’au cours du procès
lui-même. Une de ces limitations a été le bas pouvoir thermique dans l’échauffement du lit
qui a limité l’élargissement de la variété de travail en ce qui concerne la quantité des gaz
utilisés; une autre limitation a été l’incapacité de visualisation soit de l’écoulement du lit, soit
de la progression de la flamme découlant de la réaction de la combustion du propane.
Cependant, dû aux dimensions de l’installation, augmenter la puissance de l’échauffement
serait un risque et la visualisation prétendue serait compliquée à cause de l’utilisation de
matériaux qui soient résistants aux hautes températures de combustion.
VI
Agradecimentos
Agradeço em primeiro lugar ao Professor Carlos Pinho, a disponibilidade permanente, o
saber científico e a maneira como me soube orientar em todas as fases do trabalho.
Agradeço à Professora Albina Ribeiro, a ajuda a nível experimental e científico que
sempre me disponibilizou.
Agradeço à FCT, o financiamento do Projecto de Investigação Científica
POCTI/EME/44300/2002 da FCT intitulado, “Combustão e Transferência de Calor em Leitos
Fluidizados Circulantes”.
Agradeço ao PRODEP, medida 5 – acção 5.3, a bolsa que me concedeu sem a qual
não teria tido a disponibilidade de tempo necessária à realização deste trabalho.
Agradeço a todos os meus colegas do INEGI, especialmente ao Engº Vítor Ferreira, a
sua ajuda permanente na montagem da instalação experimental e no sistema de aquisição de
dados, à Engª Silvina Guimarães, pela colaboração dada na parte gráfica da elaboração da tese
e à Engª Ana Magalhães, toda a disponibilidade mostrada.
Uma palavra de agradecimento sincero aos colegas do Departamento de Engenharia
Química do ISEP, especialmente ao Engº Carlos Assis e à Engª Cristina Morais que me
ajudaram e incentivaram nas fases mais difíceis do trabalho.
Também ao Laboratório de Tecnologia Química do ISEP, desejo agradecer todo o
apoio que me foi prestado.
Por fim à minha família e, em especial aos meus filhos pelo tempo que tiveram
obrigatoriamente que me dispensar.
VII
VIII
Índice Geral
Resumo
I
Abstract
III
Résumé
V
Agradecimentos
VII
Índice Geral
IX
Índice de Figuras
XV
Índice de Tabelas
XXIII
Nomenclatura
XXVII
Capítulo 1 - Introdução
1
1.1 Enquadramento do trabalho
1
1.2 Caracterização hidrodinâmica de um leito fluidizado
4
1.2.1 Classificação de partículas
6
1.2.2 Modelo do anel
8
1.2.3 Determinação da fracção volumétrica local de sólidos
9
1.3 Modelos desenvolvidos para estimar coeficientes de transferência de calor em leitos
fluidizados
10
1.4 Influência de diferentes parâmetros na transferência de calor
12
1.5 Reactores de leitos fluidizados
13
Capítulo 2 - Projecto da Instalação Experimental
17
2.1 Definição das condições de operação pretendidas de acordo com os objectivos propostos,
materiais a usar e sua caracterização
170
2.2 Projecto do distribuidor
20
2.3 Projecto do ciclone
22
2.4 Projecto das placas de orifício para medição de caudais de gases
24
IX
2.5 Estimativa do caudal de água a circular na camisa
25
2.6 Localização dos termopares tipo K
26
2.7 Localização das tomas de pressão
27
2.8 Válvula derivadora
27
2.9 Válvula borboleta
27
Capítulo 3 – Procedimento Experimental
3.1 Preparação da areia a usar como enchimento do leito – sua caracterização
31
31
3.1.1 Caracterização da massa volúmica de cada tamanho de partículas de areia -ρP –
Método do picnómetro
32
3.1.2 Determinação da massa volúmica do leito -ρL
32
3.1.3 Porosidade mínima de fluidização
33
3.2 Ensaios de transferência de calor na coluna
34
3.3 Ensaios sem combustão
35
3.3.1 Análise da influência do caudal de água: 35 kg/h <mag < 140 kg/h
38
3.3.2 Análise da influência da Temperatura do Leito: 400ºC <TL< 700ºC
38
3.3.3 Análise da influência do caudal de ar: 0,82 kg/h <mar< 1,5 kg/h
38
3.4 Ensaios com combustão
Capítulo 4 – Análise prévia dos resultados experimentais
39
43
4.1 Regime de escoamento no leito nas condições de operação
43
4.2 Análise do calor trocado no primeiro permutador, sem combustão do propano
45
4.2.1 Estimativa da temperatura da parede interior do tubo interno do permutador
50
4.2.2 Efeito de radiação
52
4.3 Coeficiente de transferência de calor de um leito fluidizado borbulhante para um
permutador de parede membrana
X
55
4.3.1 Coeficiente de transferência de calor devido à convecção por parte do gás, hgc
57
4.3.2 Coeficiente de transferência de calor por radiação do leito para o permutador, hradL
60
4.3.3 Coeficiente de transferência de calor devido às partículas, hpc
4.4 Análise do calor trocado no primeiro permutador com combustão de propano
Capítulo 5 – Transferência de calor na ausência de combustão
5.1 Caracterização do tipo de regime no leito de partículas
63
65
71
71
5.1.1 Determinação da velocidade crítica-vc
73
5.1.2 Correlação para determinação da velocidade de transporte – vtr
74
5.1.3 Comparação dos valores de Ret, Rec, Retr e Rep em função de Ar para as diferentes
condições operatórias
75
5.2 Influência do caudal de água e da temperatura do leito na transferência de calor
83
5.3 Influência do caudal de ar na transferência de calor para a água de arrefecimento
91
5.4 Desenvolvimento de uma correlação empírica para determinação do coeficiente global
de transferência de calor do leito - hglo
96
5.4.1 Teorema Pi de Buckingham- fundamentos teóricos
97
5.4.2 Correlação empírica obtida
100
5.4.3 Análise estatística da correlação encontrada
104
5.5 Análise de tendências no valor de Nuexp
Capítulo 6 – Considerações sobre o comportamento das partículas relativamente ao calor
transferido
6.1 Análise dos resultados experimentais de hglo para cada granulometria- comparação de
resultados.
105
109
109
6.1.1 Correlações empíricas obtidas para os dois menores tamanhos e para os três maiores
112
6.2 Efeito da projecção de partículas contra a parede do permutador na transferência de
calor.
115
6.2.1 Excesso de gás
115
6.2.2 TDH
116
6.2.3 Velocidade média de subida das bolhas
118
6.2.4 Coeficiente de dispersão vertical
120
6.3 Conclusão
121
XI
Capítulo 7 – Transferência de calor com combustão de propano
125
7.1 Introdução
125
7.2 Resultados experimentais para as partículas de areia com dp=107,5 µm
127
7.3 Resultados experimentais para as partículas de areia com dp=142,5µm
132
7.4 Resultados experimentais para as partículas de areia com dp=180 µm
137
7.5 Resultados experimentais para as partículas de areia com dp=282,5 µm
143
7.6 Resultados experimentais para as partículas de areia com dp=357,5 µm
147
7.7- Análise dos resultados experimentais obtidos para todas as partículas nas condições de
combustão
7.7.1 Calor transferido para a água durante a reacção de combustão para as diferentes
granulometrias
7.7.2 Análise da tendência do Número de Nusselt para as diferentes granulometrias
durante a reacção de combustão
153
153
158
7.7.3 Correlação empírica geral
161
7.7.4 Correlação empírica simplificada
164
7.7.5 Escolha da correlação empírica final
165
7.7.6 Análise estatística da correlação geral
166
Capítulo 8 – Correlação geral para ensaios com e sem combustão
169
8.1- Comparação dos resultados obtidos para cada granulometria
169
8.2- Correlação final e análise estatística
172
8.2.1 Análise estatística
Capítulo 9 – Considerações sobre o comportamento do leito
9.1 Introdução
9.2 Determinação de uma correlação para o coeficiente de convecção das partículas, hpc
9.3 Determinação do fluxo de sólidos a partir da superfície do leito - Modelo teórico
Capítulo 10 – Conclusões e propostas de trabalho futuro.
10.1 Análise dos resultados na ausência de combustão
XII
175
177
177
178
183
193
194
10.2 Análise dos resultados com combustão
196
10.3 Resultados com e sem combustão
198
10.4 Proposta de trabalho futuro
199
11 Bibliografia
201
Apêndice I – Caracterização da areia
207
A.I.1 Características das partículas
207
A.I.2 Velocidade mínima de fluidização e velocidade terminal de uma partícula em função
da temperatura
208
Apêndice II – Calibração dos aparelhos de medida e respectivas incertezas
215
AII.1 Calibração dos transdutores usados na determinação da queda de pressão no leito
fluidizado e ao longo da zona de transporte.
215
A.II.2 Calibração dos medidores de caudal de gás
218
A.II.2.1 Calibração da placa orifício para o propano e do rotâmetro para o CO2
219
A.II.2.2 Calibração da placa orifício para o ar
228
A.II.3 Calibração dos aparelhos de medida para o caudal de água
233
A.II.3.1 Debitómetro de turbina
233
A.II.3.2 Rotâmetro
235
Apêndice III – Análise de incertezas
239
Apêndice IV – Propriedades da mistura gasosa
243
A.IV.1 Estimativa da composição da mistura gasosa
243
A.IV.2 Propriedades dos componentes puros
248
A.IV3 Cálculo das propriedades da mistura gasosa
253
A.IV.4 Expressões usadas para cálculo das propriedades físicas do ar
255
Apêndice V – Tabelas de dados e resultados experimentais
257
XIII
Índice de Figuras
Capítulo 1
Figura 1.1
Zonas características de um leito fluidizado, Rhodes (1998)
6
Figura 1.2
Classificação das partículas segundo Geldart, para fluidização com ar à
temperatura ambiente e para v0<vmf, Kunii e Levenspiel (1991)
7
Capítulo 2
Figura 2.1
Esquema de um separador ciclónico
23
Figura 2.2
Fotografia da instalação experimental
28
Figura 2.3
Fotografia da instalação experimental com a respectiva legenda
29
Figura 2.4
Desenho da instalação referente à zona de trabalho e dimensões mais
importantes
30
Figura 3.1
Visualização do ecrã do PC durante um dos ensaios sem combustão
TL=600 ºC
35
Figura 3.2
Esquema da instalação experimental
37
Figura 4.1
Variação da entalpia do ar e da água para as condições de operação,
TL=700 ºC; PL=10 cm; mar=1 kg/h; dp =180 µm; mag = 35 kg/h
46
Figura 4.2
Variação da entalpia do ar e da água para as condições de operação,
TL=700 ºC; PL=10 cm; mar=1 kg/h; dp =180 µm; mag =73 kg/h
47
Figura 4.3
Variação da entalpia do ar e da água para as condições de operação,
TL=700 ºC; PL =10 cm; mar =1 kg/h; dp =180 µm; mag =140 kg/h
47
Figura 4.4
Variação da entalpia do ar e da água para as condições de operação,
TL=700 ºC; PL =13 cm; mar =1 kg/h; dp =180 µm; mag =73 kg/h, com corte de
ar
49
Figura 4.5
Esquema para identificação das superfícies envolvidas na troca de calor por
radiação
61
Figura 4.6
Circuito térmico equivalente para a troca de calor por radiação entre a zona
do leito e o permutador, RL- resistência de radiação do leito;
Resp- Resistência espacial de radiação; RP- resistência de radiação do
permutador
62
Variação da pressão num leito fluidizado em função da velocidade
superficial do gás. Zonas de transição caracterizadas pela velocidade vc e vk.,
Rhodes (1996)
72
Capítulo 3
Capítulo 4
Capítulo 5
Figura 5.1
XV
Figura 5.2
Variação da raiz quadrada da pressão e da densidade do leito com a
velocidade superficial do gás de acordo com vários regimes:
B – borbulhante; Tr – Transição; T – Turbulento, Rhodes (1996)
reproduzido por Horio et al (1992)
73
Figura 5.3
Valores para Rep, Ret, Rec, Retr em função de Ar para as condições
operatórias e partículas dp=107,5 µm.
76
Figura 5.4
Valores para Rep, Ret, Rec, Retr em função de Ar para as condições
operatórias e partículas dp=142,5 µm
76
Figura 5.5
Valores para Rep, Ret, Rec, Retr em função de Ar para as condições
operatórias e partículas dp=180 µm
77
Figura 5.6
Valores para Rep, Ret, Rec, Retr em função de Ar para as condições
operatórias e partículas dp=282,5 µm
77
Figura 5.7
Valores para Rep, Ret, Rec, Retr em função de Ar para as condições
operatórias e partículas dp=357,5 µm
78
Figura 5.8
Mapa de regime de fluidização num leito de partículas, Wen-Ching (2003)
79
Figura 5.9
Rácio v0/vmf, caudal de ar entre 0,82 < mar (kg/h) < 1,5 para a TL = 400 ºC
80
Figura 5.10
Rácio v0/vmf, caudal de ar entre 0,82 < mar (kg/h) < 1,5 para a TL= 500 ºC
81
Figura 5.11
Rácio v0/vmf , caudal de ar entre 0,82 < ma r(kg/h) < 1,5 para a TL= 600 ºC
81
Figura 5.12
Rácio v0/vmf , caudal de ar entre 0,82 < mar(kg/h) < 1,5 para a TL= 700 ºC
82
Figura 5.13
Variação da entalpia do ar e da água para dois caudais de água distintos, no
caso de TL = 400ºC, mar = 1 kg/h, PL= 12 cm, vo/vmf = 22; dp=107,5 µm
84
Figura 5.14
Variação da entalpia do ar e da água para dois caudais de água distintos, no
caso de TL= 660ºC, mar = 1 kg/h, PL= 13 cm, vo/vmf = 37; dp=107,5 µm
84
Figura 5.15
Variação da entalpia do ar e da água para dois caudais de água distintos, no
caso deTL= 500ºC, mar = 1 kg/h, PL= 16 cm, vo/vmf = 13; dp=142,5 µm.
85
Figura 5.16
Variação da entalpia do ar e da água para três caudais de água distintos, no
caso de TL= 700ºC, mar = 1 kg/h, PL= 10 cm, vo/vmf = 19; dp=180 µm
85
Figura 5.17
Variação da entalpia do ar e da água para dois caudais de água distintos, no
caso de TL= 700ºC, mar = 1 kg/h, PL= 9 cm, vo/vmf = 6; dp=282,5 µm
86
Figura 5.18
Variação da entalpia do ar e da água para dois caudais de água distintos, no
caso de TL= 700ºC, mar = 1 kg/h, PL= 8 cm, vo/vmf = 4; dp=357,5 µm
86
Figura 5.19
Valores médios da variação da entalpia da água em função de TL
89
Figura 5.20
Valores médios da diferença entre variação da entalpia da água e do ar
função de TL
89
Figura 5.21
Valores médios do calor axial em função de TL
90
XVI
Figura 5.22
Variação da temperatura da água em função da temperatura do leito para
vários caudais de ar, dp=107,5 µm
92
Figura 5.23
Variação da temperatura da água em função da temperatura do leito para
vários caudais de ar, dp=142,5 µm
92
Figura 5.24
Variação da temperatura da água em função da temperatura do leito para
vários caudais de ar, dp=180 µm
93
Figura 5.25
Variação da temperatura da água em função da temperatura do leito para
vários caudais de ar, dp=282,5 µm
93
Figura 5.26
Variação da temperatura da água em função da temperatura do leito para
vários caudais de ar, dp=357,5 µm
94
Figura 5.27
Valores de Nuexp e ajuste linear de Nucalc versus Nuexp, 99 observações
102
Figura 5.28
Desvio de ± 25% da correlação 5.17 relativamente à recta y = x
104
Figura 5.29
Recta de ajuste e limites de 95% de confiança para a correlação empírica
5.17
105
Figura 5.30
Variação de Nuexp versus TL para todas as condições de operação sem
combustão
106
Figura 5.31
Variação de Nuexp versus v0/vmf para todas as condições de operação sem
combustão
107
Figura 5.32
Variação de Nuexp versus ∆TlnL-w para todas as condições de operação sem
combustão
108
Figura 6.1
Valores do coeficiente global de transferência de calor hgloexp versus ∆TlnL-w.
110
Figura 6.2
Valores do coeficiente global de transferência de calor hgloexp versus ∆TlnL-w
dp = 107,5 µm e dp = 142,5 µm
111
Figura 6.3
Valores do coeficiente global de transferência de calor hgloexp versus ∆TlnL-w
para dp = 180 µm; dp = 282,5 µm e dp = 357,5 µm
111
Figura 6.4
Nucalc versus Nuexp para as partículas de dp=107,5 µm e dp=142,5µm- e 42
observações
113
Figura 6.5
Nucalc versus Nuexp para as partículas de dp=180 µm, dp=282,5 µm e
dp=357,5 µm e 57 observações
114
Figura 6.6
Nucalc pelas equações 6.1 e 6.2 versus Nuexp e 99 observações
114
Figura 6.7
Nucalc pela equação 6.3 versus Nuexp e 99 observações.
116
Figura 6.8
Nucalc pela equação 6.4 versus Nuexp e 99 observações
118
Capítulo 6
XVII
Figura 6.9
Nucalc pela equação 6.8 versus Nuexp e 99 observações
120
Figura 6.10
Nucalc pela equação 6.10 versus Nuexp e 99 observações
121
Figura 7.1
Variação da entalpia da corrente gasosa e da água para um ensaio com
combustão do propano. t1 – introdução do propano ao caudal de 0,095 kg/h;
t2 - aumento do caudal de ar para 1kg/h sem aumentar o propano;
t3 - corte de propano; t4 - corte de ar; dp=107,5 µm
128
Figura 7.2
Variação da pressão no leito versus tempo, dp=107,5 µm
128
Figura 7.3
Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.1;
dp=107,5 µm
129
Figura 7.4
Variação da entalpia da corrente gasosa e da água para um ensaio com
combustão do propano. t1 - introdução do propano ao caudal de 0,09 kg/h; t2
- aumento do caudal de ar para 0,98 kg/h e do caudal de propano para 0,1
kg/h; t3 - corte de propano; t4 - corte de ar ; dp=107,5 µm
130
Figura 7.5
Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.2;
dp=107,5 µm
130
Figura 7.6
Variação da entalpia da corrente gasosa e da água para o ensaio com
combustão do propano. t1 – introdução do propano ao caudal de 0,1 kg/h; t2 corte de propano; t3 - corte de ar; dp=142,5 µm
133
Figura 7.7
Variação da pressão do leito versus tempo correspondente à Tabela 7.4;
dp=142,5 µm
133
Figura 7.8
Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.4;
dp=142,5 µm
134
Figura 7.9
Variação da entalpia da corrente gasosa e da água para um ensaio com
combustão do propano. t1 – introdução do propano ao caudal de 0,09 kg/h;
t2- aumento do caudal de ar para 0,98 kg/h sem aumentar o propano;
t3 - corte de propano; t4 - corte de ar; dp=142,5 µm
135
Figura 7.10
Variação da pressão do leito versus tempo correspondente à Tabela 7.5;
dp=142,5 µm
135
Figura 7.11
Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.5;
dp=142,5 µm
136
Figura 7.12
Variação da entalpia da corrente gasosa e da água para um ensaio com
combustão do propano (caudal de ar inicial 1kg/h). t1 – introdução do
propano ao caudal de 0,1 kg/h; t2 - aumento do caudal de ar para 1,2 kg/h e
aumento do caudal de propano para 0,13 kg/h; t3 - corte de propano; t4 –
corte de ar; dp=180 µm
138
Figura 7.13
Variação da pressão no leito versus tempo correspondente à Tabela 7.7;
dp=180 µm
138
Figura 7.14
Perfil de temperatura corrigidas dos gases correspondente à Tabela 7.7;
dp=180 µm
139
Capítulo 7
XVIII
Figura 7.15
Variação da entalpia da corrente gasosa e da água para um ensaio com
combustão do propano (caudal de ar inicial 1,2 kg/h). t1 - introdução do
propano ao caudal de 0,12 kg/h; t2 - corte de propano; t3- corte de ar; dp=180
µm
140
Figura 7.16
Variação da pressão no leito versus tempo correspondente à Tabela 7.8;
dp=180 µm
140
Figura 7.17
Perfil de temperaturas corrigidas dos gases durante o ensaio correspondente
à Tabela 7.8; dp=180 µm
141
Figura 7.18
Variação da entalpia da corrente gasosa e da água correspondente à Tabela
7.10; dp=282,5 µm
144
Figura 7.19
Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.10 ;
dp=282,5 µm
145
Figura 7.20
Variação da entalpia da corrente gasosa e da água correspondente à Tabela
7.11; dp=282,5 µm
146
Figura 7.21
Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.11
dp=282,5 µm
146
Figura 7.22
Variação da entalpia da corrente gasosa e da água correspondente à Tabela
7.13; dp=357,5 µm
149
Figura 7.23
Perfil de temperaturas corrigidas dos gases durante o ensaio correspondente
à Tabela 7.13; dp=357,5 µm
149
Figura 7.24
Variação da entalpia da corrente gasosa e da água correspondente à Tabela
7.14; dp=357,5 µm
150
Figura 7.25
Perfil de temperaturas corrigidas dos gases durante o ensaio correspondente
à Tabela 7.14; dp=357,5 µm
151
Figura 7.26
Valores médios da variação da entalpia da água em função do diâmetro das
partículas para mar=1kg/h e mpro=0,1 kg/h.
157
Figura 7.27
Variação de qag para as diferentes granulometrias e para dois caudais de ar
diferentes sendo A/C =10.
158
Figura 7.28
Variação de qag para as diferentes granulometrias e para dois caudais de ar
diferentes sendo A/C = 9.4 e A/C = 10
158
Figura 7.29
Valores médios de Nuexp versus TL para todos os ensaios realizados com
combustão
160
Figura 7.30
Valores médios de Nuexp versus TL para todos os ensaios realizados
correspondentes à mesma fase de queima de propano
161
Figura 7.31
Valores experimentais para todos os ensaios com combustão, ajuste linear
de Nucal versus. Nuexp e 42 observações
162
XIX
Figura 7.32
Desvio de ±20% relativamente à recta y = x
163
Figura 7.33
Recta de ajuste e limites de confiança de 95% para a correlação empírica
7.2.
167
Figura 8.1
Variação de Nuexp versus ∆TlnL-w para dp= 107, µm
169
Figura 8.2
Variação de Nuexp versus ∆TlnL-w para dp= 142,5 µm
170
Figura 8.3
Variação de Nuexp versus ∆TlnL-w para dp= 180 µm
170
Figura 8.4
Variação de Nuexp versus ∆TlnL-w para dp= 282,5 µm
171
Figura 8.5
Variação de Nuexp versus ∆TlnL-w para dp= 357,5 µm
171
Figura 8.6
Valores experimentais com e sem combustão no leito, e ajuste linear de
Nucal versus Nuexp- 141 observações
173
Figura 8.7
Desvio de ± 20% da correlação 8.1 relativamente à recta y = x.
174
Figura 8.8
Recta de ajuste, limites de confiança de 95% para a correlação 8.1.
175
Figura 9.1
Valores experimentais de hpc versus (v0-vmf)/vmf para os ensaios sem
combustão
179
Figura 9.2
Valores experimentais de hpc versus (v0-vmf)/vmf para os ensaios com
combustão
180
Figura 9.3
Valores experimentais de hpc versus (v0-vmf)/vmf para os ensaios sem e com
combustão
181
Figura 9.4
Valores de Nup versus Nupm para todas as granulometrias e 121 observações
183
Figura 9.5
Projecção de sólidos à superfície do leito: a) a partir do topo da bolha; b) a
partir da esteira de uma única bolha; c) a partir da esteira de duas bolhas que
coalescem, Wen-Ching(2003).
184
Figura 9.6
Fluxo de partículas versus excesso de gás para ensaios com e sem
combustão, 113 observações
186
Figura 9.7
Fluxo de partículas experimental e previsto pelo modelo nos ensaios sem
combustão
190
Figura 9.8
Fluxo de partículas experimental e previsto pelo modelo nos ensaios com
combustão
191
Figura 9.9
Fluxo de partículas versus excesso de gás para as três menores dimensões
nos ensaios sem combustão
192
Capítulo 8
Capítulo 9
XX
Apêndice I
Figura A.I.1
vmf = f(T) para dp = 180 µm
210
Figura A.I.2
vt = f(T) para dp = 180 µm
211
Figura A.I.3
vmf = f(T) para dp = 107,5µm
211
Figura A.I.4
vt = f(T) para dp = 107,5 µm.
211
Figura A.I.5
vmf = f(T) para dp = 142,5 µm
212
Figura A.I.6
vt= f(T) para dp = 142,5 µm
212
Figura A.I.7
vmf= f(T) para dp = 282,5 µm
212
Figura A.I.8
vt= f(T) para dp = 282,5 µm
213
Figura A.I.9
vmf= f(T) para dp = 357,5 µm
213
Figura A.I.10
vt= f(T) para dp = 357,5 µm
213
Figura A.II.1
Esquema de instalação para calibração dos transdutores de pressão
diferencial
216
Figura A.II.2
Transdutor 1-Curva de calibração do PX143-05BD5V
216
Figura A.II.3
Transdutor 2- Curva de calibração do transdutor PX142-005D5V
217
Figura A.II.4
Transdutor 3- Curva de calibração do transdutor PX142-002D5V
217
Figura A.II.5
Esquema de instalação da posição dos transdutores na coluna
218
Figura A.II.6
Esquema da instalação usada na calibração das placas orifício para o
propano e para um rotâmetro 2D-150S para medição do caudal de CO2,
Método do deslocamento positivo
221
Figura A.II.7
Curva de calibração do rotâmetro 2D 150S, com CO2 à pressão relativa de 1
bar, utilizando o método do deslocamento positivo
223
Figura A.II.8
Curva de calibração do medidor de orifício para propano, dor = 2,95 mm à
pressão relativa de 1 bar , utilizando o método do deslocamento positivo
224
Figura A.II.9
Curva de calibração do medidor de orifício para propano, dor = 1 mm à
pressão relativa de 400 mbar, utilizando o método do deslocamento
positivo.
224
Figura A.II.10
Incerteza do caudal mássico de CO2 para cada posição do rotâmetro
227
Figura A.II.11
Incerteza do caudal mássico de propano
228
Figura A.II.12
Esquema da instalação usada para calibrar as placas orifício correspondente
ao ar usando um analisador de CO2
229
Apêndice II
XXI
Figura A.II.13
Curva de calibração da placa orifício com dor = 5 mm para ar à pressão
relativa de 1 bar recorrendo ao analisador de CO2
231
Figura A.II.14
Curva de calibração da placa orifício com dor = 5 mm para ar à pressão
relativa de 400 mbar recorrendo ao analisador de CO2
231
Figura A.II.15
Incerteza do caudal volumétrico do ar
233
Figura A.II.16
Curva de calibração do debitómetro de turbina para medição do caudal de
água
234
Figura A.II.17
Curva de calibração do rotâmetro para a Prel = 1.5 bar para medição do
caudal de água
236
Figura A.II.18
Incerteza do caudal mássico de água
237
Figura A.IV.1
Variação da condutibilidade térmica com a temperatura para o CO2
248
Figura A.IV.2
Variação da viscosidade com a temperatura para o CO2
248
Figura A.IV.3
Variação da condutibilidade térmica com a temperatura para o CO
249
Figura A.IV.4
Variação da viscosidade com a temperatura para o CO
249
Figura A.IV.5
Variação da condutibilidade térmica com a temperatura para H2O
250
Figura A.IV.6
Variação da viscosidade com a temperatura para o H2O
250
Figura A.IV.7
Variação da condutibilidade térmica com a temperatura para H2
251
Figura A.IV.8
Variação da viscosidade com a temperatura para o H2
251
Figura A.IV.9
Variação da condutibilidade térmica com a temperatura para N2
252
Figura A.IV.10
Variação da viscosidade com a temperatura para o N2
252
Figura A.IV.11
Variação da condutibilidade térmica com a temperatura para o ar
256
Apêndice IV
XXII
Índice de Tabelas
Capítulo 2
Tabela 2.1.
Coeficiente do orifício em função do número de Reynolds (Kunii e
Levenspiel (1991))
21
Tabela 2.2.
Parâmetros para projecto do ciclone, Macintyre (1988)
23
Tabela 2.3.
Resultados obtidos para as três placas de orifício
25
Valores das velocidades terminais em função do diâmetro médio das
partículas, para as temperaturas do leito usadas
44
Tabela 5.1.
Temperatura máxima atingida no leito para os diversos caudais de ar e
diferentes granulometrias
83
Tabela 5.2.
Valores médios das entalpias das duas correntes, da diferença entre elas e do
calor axial em função de temperatura do leito para dp=107,5 µm
87
Tabela 5.3.
Valores médios das entalpias das duas correntes, da diferença entre elas e do
calor axial em função de temperatura do leito para dp=142,5 µm
87
Tabela 5.4.
Valores médios das entalpias das duas correntes, da diferença entre elas e do
calor axial em função de temperatura do leito para dp=180 µm
88
Tabela 5.5.
Valores médios das entalpias das duas correntes, da diferença entre elas e do
calor axial em função de temperatura do leito para dp=282,5 µm
88
Tabela 5.6.
Valores médios das entalpias das duas correntes, da diferença entre elas e do
calor axial em função de temperatura do leito para dp=357,5 µm
88
Tabela 5.7.
Variáveis escolhidas para a análise dimensional
98
Tabela 5.8.
Estimativas finais dos parâmetros da correlação (5.17) e sua importância
relativa - método de optimização “NLREG”
103
Tabela 6.1.
Correlações empíricas para 107,5 < dp(µm) < 357,5 e Pr = 0,73
122
Tabela 6.2.
Correlações empíricas para 107,5
180 < dp(µm) < 357,5 e Pr = 0,73
Capítulo 4
Tabela 4.1.
Capítulo 5
Capítulo 6
<
dp(µm)
<
142,5
e
para
123
Tabela 7.1.
Valores médios para qgas e qag no ensaio com combustão, dp = 107,5 µm,
caudal de água de 73 kg/h
127
Tabela 7.2.
Valores médios para qgas e qag no ensaio com combustão, dp = 107,5 µm,
caudal de água de 35 kg/h
129
Tabela 7.3.
Valores experimentais para os ensaios de combustão, dp=107,5 µm
131
Capítulo 7
XXIII
Tabela 7.4.
Valores médios para qgas e qag no ensaio com combustão, dp = 142,5 µm,
caudal de água de 73 kg/h
132
Tabela 7.5.
Valores médios para qgas e qag no ensaio com combustão, dp = 142,5 µm,
caudal de água de 35 kg/h
132
Tabela 7.6.
Valores experimentais para os ensaios de combustão com as partículas de
dp=142,5 µm
136
Tabela 7.7.
Valores médios para qgas e qag no ensaio com combustão, dp = 180 µm,
caudal de água de 73 kg/h
137
Tabela 7.8.
Valores médios para qgas e qag no ensaio com combustão, dp = 180 µm,
caudal de água de 73 kg/h.
139
Tabela 7.9.
Valores experimentais para os ensaios de combustão com as partículas
dp=180 µm
Tabela 7.10.
Valores médios para qgas e qag no ensaio com combustão, dp = 287,5 µm,
caudal de água de 73 kg/h
144
Tabela 7.11.
Valores médios para qgas e qag no ensaio com combustão, dp = 282,5 µm,
caudal de água de 73 kg/h
145
Tabela 7.12.
Valores experimentais para os ensaios de combustão com as partículas de
dp=282,5 µm
147
Tabela 7.13.
Valores médios para qgas e qag no ensaio com combustão, dp = 357,5 µm,
caudal de água de 73 kg/h
148
Tabela 7.14.
Valores médios para qgas e qag no ensaio com combustão, dp = 357,5 µm,
caudal de água de 73 kg/h
150
Tabela 7.15.
Valores experimentais para os ensaios de combustão com as partículas de
dp=357,5 µm.
152
Tabela 7.16.
Estimativas finais dos parâmetros da correlação 7.2 e sua importância
relativa –Método de optimização de “NLREG”
164
Tabela 7.17.
Estimativas finais dos parâmetros da correlação 7.4 e sua importância
relativa –Método de optimização de “NLREG”
165
Estimativas finais dos parâmetros da correlação 8.1 e sua importância
relativa - método de optimização “NLREG
174
Tabela A.I.1
Características das partículas de areia
207
Tabela A.I.2
Resultados obtidos para determinação de vmf = f(T) usando a equação A.I.1
para as partículas de dp=180 µm
209
Tabela A.I.3
Resultados obtidos para determinação de vt = f(T) usando a equação A.I.4 e
A.I.5 para as partículas de dp=180 µm
210
Incertezas associadas às curvas de calibração dos transdutores
218
142
Capítulo 8
Tabela 8.1.
Apêndice I
Apêndice II
Tabela A.II.1
XXIV
Apêndice III
Tabela A.III.1
Incerteza relativa nos valores de hgloexp
241
Apêndice IV
Tabela A.IV.1
Variação da constante de dissociação kp´ com a temperatura do leito
246
Tabela A.IV.2
Número de moles de cada componente correspondente à reacção (4.21) para
r =1,6 e às diferentes temperaturas médias do leito
246
Tabela A.IV.3
Número de moles de cada componente correspondente à reacção (4.21) para
r =1,8 e às diferentes temperaturas médias do leito
247
Tabela A.IV.4
Número de moles e fracção molar de cada componente a usar na avaliação
das propriedades da mistura gasosa
247
Tabela A.IV.5
Variação da condutibilidade térmica da mistura gasosa com a temperatura do
filme
254
Tabela AIV.6
Variação da viscosidade da mistura gasosa com a temperatura do filme
255
Tabela A.V.1 a
A.V.5
Dados experimentais obtidos nos ensaios sem combustão para todas as
granulometrias
258
Tabela A.V.6 a
A.V.10
Resultados experimentais das variáveis usados na correlação 5.17 para todas
as granulometrias
263
Tabela A.V.11 a
A.V.15
Dados experimentais obtidos nos ensaios com combustão para todas as
granulometrias
268
Tabela A.V.16 a
A.V.20
Resultados experimentais das variáveis usados na correlação 7.2 para todas
as granulometrias
271
Apêndice V
XXV
Nomenclatura
Variável
Descrição
Unidade
Ae
Área exterior do permutador para transferência de calor
Aesc
Área da secção recta da coluna
m2
AL
Área total do leito definida no modelo de radiação
m2
Ap
Área do permutador para transferência de calor
m2
Ar
-
(A/C)est
Número de Arquimedes ( (ρp-ρg) ρgdp3g/ µg2))
(Caudal mássico de ar /caudal mássico de propano) estequiométrico
(A/C)real
(Caudal mássico de ar /caudal mássico de propano) real
-
Bx
Incerteza sistemática associada à medição da grandeza x
-
cdor
Coeficiente de descarga do orifício
-
cD
Coeficiente de arrasto
-
cp
Calor específico da água a pressão constante
J/kg K
cpg
Calor específico do gás a pressão constante
J/kg K
cs
Calor específico da areia
J/kg K
cv
Concentração volumétrica de partículas (1-ε)
Diâmetro do ciclone
Dcicl
-
-
m
2
Ddv
Coeficiente de dispersão vertical
m /s
Dm
Desvio médio
%
dBVS
Diâmetro equivalente de uma bolha à superfície do leito
m
dc
Diâmetro de uma nuvem de partículas
m
de
Diâmetro exterior do tubo interno da coluna
m
deq
Diâmetro equivalente do lado da água
m
di
Diâmetro interno da coluna
m
d0r
Diâmetro do orifício
m
dp
Diâmetro médio das partículas
m
1/3
-
d p*
Parâmetro adimensional (Ar )
dtp
Diâmetro do termopar
dágua,4
Densidade da água a 4ºC
-
Densidade da areia referida à água a 4ºC
-
Densidade da areia referida à água a 20ºC
-
d4
20
d20
Eg
20
c
Energia cinética do gás
m
W
E0
Fluxo total de partículas arrastado na superfície do leito
kg/sm2
E0m
Fluxo de sólidos à superfície do leito previsto pelo modelo
kg/sm2
E∞
Fluxo total de partículas arrastado acima de TDH
kg/sm2
Fi,j
Factor de forma para a radiação
-
XXVII
Variável
Descrição
Unidade
Fr
Número de Froude ( v0 / gdi )
-
Frt
Número de Froude terminal ( vt / gd i )
-
Gr
Número de Grashoff ( (gβ(Tm − Tw )d i 3
Gz
Número de Graetz ( RePrdi/Lp )
g
Aceleração da gravidade
H
Altura da coluna
m
Hc
Altura total do ciclone
m
Hmt
Altura mínima do leito para ocorrer a formação de bolhas tubulares
he
(µ ρ)
2
Coeficiente de convecção do lado da água
hL
Altura do leito
m/s2
m
2
W/m K
cm
Coeficiente global de transferência de calor do lado interno da coluna
W/m2K
hglot
Coeficiente global de transferência de calor calculado
W/m2K
hgc
Coeficiente de transferência de calor por convecção devido ao gás
W/m2K
hmf
Altura mínima de fluidização
hpc
Coeficiente de transferência de calor por convecção devido às partículas
W/m2K
hpct
Coeficiente de transferência de calor por convecção devido às partículas
calculado
Coeficiente de transferência de calor por convecção do termopar
W/m2K
hglo
exp
-
))
htp
hradL
m,cm
W/m2K
W/m2K
kg
Coeficiente de transferência de calor por radiação do leito para o
permutador
Coeficiente de transferência de calor por radiação devido ao meio
participante
Condutibilidade térmica do gás
Kp
Constante de dissociação em termos de pressões parciais
-
kp´
Constante de dissociação em termos de moles dos componentes
-
Lc
Altura do ciclone correspondente à parte cilíndrica
m
Lh
Comprimento de entrada hidrodinâmico
m
Lmr
Percurso médio de radiação
m
Lp
Altura de cada permutador
m
Lt
Comprimento de entrada térmico
m
Ltp
Comprimento do termopar
m
Mar
Massa molecular do ar
mag
Caudal mássico de água na camisa de arrefecimento
kg/s
mar
Caudal mássico total de ar
kg/s
mareia
Massa de areia
mg
Caudal mássico de gás
kg/s
mpro
Caudal mássico de propano
kg/s
ms
Caudal mássico total de areia à superfície do leito
kg/s
N
Número de orifícios por unidade de área do distribuidor
Ne
Número de espirais para projecto do ciclone
hrmp
XXVIII
W/m2K
W/mK
kg/kmol
kg
m-2
-
Variável
Descrição
Unidade
Nucalc
Número de Nusselt calculado
-
Nucom
Número de Nusselt combinado
-
Nue
Número de Nusselt do lado da água( he deq/kag)
-
Nuexp
Número de Nusselt experimental ( hglo di/kg)
-
Nuf
Número de Nusselt para convecção forçada
-
Nun
Número de Nusselt para convecção natural
-
Nup
Nup
Número de Nusselt da partícula (hpc di/kg)
m
t
Número de Nusselt da partícula calculado (hpc di/kg)
-
Nutp
Número de Nusselt para referido ao termopar (htp dtp/kg)
-
n
Número de observações
-
ni
Número de moles do componente i
nor
Número de orifícios na placa do distribuidor
P
Pressão diferencial
Pa
Pressão ambiente
Pd
Pressão no distribuidor
cmH2O
PL
Pressão no leito
cmH2O
Pm
Perímetro molhado para transferência de calor
Px
Incerteza aleatória associada à medição da grandeza x
-
Pr
Número de Prandtl
-
Prob (t)
Variável estatística
-
pf
Posição do flutuador no rotâmetro
kmol
mmH2O
Pa
m
3
Qar
Caudal volúmico do ar
m /s
QCO2
Caudal volúmico de CO2
m3/s
Q20ºC
Caudal volúmico do ar a 20ºC e 1 atm
m3/s
qag
Potência térmica recebida pela água
W
qar
Potência térmica cedida pelo ar
W
qaxial
Potência térmica axial
W
qgas
Potência térmica cedida pelos gases resultantes da combustão
W
q
exp
Potência térmica experimental das partículas
W
qtp
Potência térmica teórica das partículas
W
qradL
Potência térmica de radiação entre leito e parede
W
qrmp
Potência térmica de radiação entre leito e parede em meio participante
W
R
Constante dos gases perfeitos
Rcond
Resistência térmica de condução
K/W
Resp
Resistência espacial de radiação
m-2
RL
Resistência do leito à radiação
m-2
Rp
Resistência da parede do permutador à radiação
m-2
Rear
Número de Reynolds nas condições de escoamento (ρg v0 di/µg)
-
Rec
Número de Reynolds crítico(ρg vc di/µg)
-
p
J/kg mol.K
XXIX
Variável
Descrição
Unidade
Remf
Número de Reynolds mínimo de fluidização (ρg vmfdp/µg)
-
Rep
Número de Reynolds da partícula (ρg v0dp/µg)
-
Ret
Número de Reynolds terminal (ρg vtdp/µg)
-
Retp
Número de Reynolds para o termopar (ρg v0dtp/µg)
-
Retr
-
r
Número de Reynolds de transporte (ρg vtrdp/µg)
Riqueza da mistura
Ta
Temperatura ambiente
ºC
Tarreal
Temperatura real do ar
ºC
Tage
Temperatura de entrada da água
ºC
Tags
Temperatura de saída da água
ºC
Td
Temperatura do distribuidor
K
Tf
Temperatura do filme
ºC
Tge
Temperatura do gás à entrada
ºC
Tgs
Temperatura do gás à saída
ºC
corr
Temperatura do gás à entrada corrigida
ºC
corr
Temperatura do gás à saída corrigida
Tge
Tgs
-
ºC
corr
Tin
Temperatura adimensional ((TL-Tw)/(TL-Tgs
TL
Temperatura do leito
Tm
Temperatura média do gás entre entrada e saída
ºC
Tmag
Temperatura média da água entre a entrada e a saída
ºC
TmL-p
Temperatura média entre leito e parede
ºC
Ts
Temperatura da suspensão
ºC
Ttp
Temperatura registada pelo termopar
ºC
Tw
Temperatura da parede do tubo interno
ºC
Twe
Temperatura da parede externa do tubo interno
ºC
Twi
Temperatura da parede interna do tubo interno
ºC
TDH
Altura da zona de transporte
m
t
Variável t de Student
-
Ux
Incerteza total associada à medição da grandeza x
-
Vt
Volume total da massa de areia
mL
va
Velocidade média de admissão do ar no ciclone
m/s
vc
Velocidade crítica das partículas
m/s
vk
Velocidade de transição
m/s
vmb
Velocidade média de subida das bolhas
m/s
vmf
Velocidade mínima de fluidização
m/s
vmt
Velocidade média do gás para formação de bolhas tubulares
m/s
v0
Velocidade superficial do gás
m/s
v0r
Velocidade no orifício
m/s
vt
Velocidade terminal das partículas
m/s
XXX
))
ºC,K
Variável
Descrição
Unidade
vtr
Velocidade de transporte das partículas
m/s
v*
Velocidade adimensional ((v0-vmf)/(vt-vmf))
-
xi
Fracção molar do componente i
-
Zc
Altura do ciclone correspondente à parte cónica
m
Letras Gregas
αg
Absortividade do gás
ρag
Massa volúmica da água
kg/m3
ρar
Massa volúmica do ar
kg/m3
ρg
Massa volúmica do gás
kg/m3
ρL
Massa volúmica do leito
kg/m3
ρp
Massa volúmica das partículas
kg/m3
µag
Viscosidade dinâmica da água
Pa.s
µg
Viscosidade dinâmica do gás
Pa.s
µw
Viscosidade dinâmica da água à temperatura da parede
Pa.s
εc
Emissividade das nuvens de partículas
-
εg
Emissividade do gás
-
εL
Emissividade do leito
-
εmf
Porosidade mínima de fluidização
-
εp
Emissividade da parede do permutador
-
εpart
Emissividade das partículas
-
εs
Emissividade da suspensão
-
εtp
Emissividade do termopar
-
εw
Emissividade da parede do leito
-
∆ε
Factor de correcção da emissividade da mistura gasosa
-
∆α
Factor de correcção da absortividade da mistura gasosa
-
∆Pcicl.
Diferença de pressão no ciclone
∆PL
Diferença de pressão no leito
cmH2O
∆Pd
Diferença de pressão no distribuidor
cmH2O
∆Pmf
Queda de pressão em condições mínimas de fluidização
cmH2O
∆Tag
Variaçãp da temperatura da água (Tags-Tage)
ºC
∆TlnL-w
Média logarítmica da diferença de temperaturas entre entrada e saída do
permutador para temperatura da parede constante ((TL-Tgscorr)/ln((TLTw)/(Tgscorr-Tw)))
ºC
-
mmH2O
XXXI
1. Introdução
1.Introdução
1.1 Enquadramento do trabalho
A necessidade de se recorrer a fontes energéticas que permitam uma redução no
controlo das emissões de CO2 tem levado os investigadores, as autoridades e os políticos em
geral, a virarem a sua atenção para as fontes energéticas ditas renováveis e para o estudo de
sistemas de queima adequados às novas limitações ambientais.
Actualmente, 15% da energia primária consumida pela Humanidade, principalmente
para a produção de energia térmica ou calor útil, provém da madeira e de resíduos lenhosos,
se bem que na maioria dos casos os processos de combustão deixem muito a desejar. Por
outro lado, o interesse nesta forma de energia tem vindo a aumentar de tal modo que os
objectivos propostos para a União Europeia, no que diz respeito à bioenergia, são bastante
ambiciosos (EEA, 2006).
A utilização de biomassa como fonte energética pela via de combustão poderá ser
encarada sob duas ópticas. Através do cultivo de espécies de crescimento rápido, destinados
exclusivamente à combustão, ou através do uso de resíduos agrícolas ou florestais. De
qualquer modo, após a energia hidroeléctrica e a energia eólica, a biomassa aparece como a
fonte energética renovável de maior interesse para a União Europeia.
Convém referir que qualquer que seja a aproximação adoptada, produção dedicada de
biomassa para a queima, ou simplesmente recurso aos resíduos, esta produção de energias
úteis (electricidade e calor) se fará recorrendo a um ciclo fechado de CO2, por oposição à
situação agora frequente de se recorrer à queima de combustíveis fósseis, a qual liberta
grandes quantidades de carbono que passam para atmosfera sob a forma de dióxido de
carbono, com os problemas climáticos conhecidos de todos.
1
1. Introdução
Haverá situações em que se pode aplicar a co-combustão de resíduos de biomassa ou
florestais com lamas das ETAR, ou com efluentes gasosos dos aterros sanitários, ou ainda
com combustíveis de origem fóssil, existindo pois uma multiplicidade de combinações que
justificam o interesse renovado da biomassa como fonte energética.
O estudo das tecnologias de queima de biomassa e processos físico-químicos afins
revela-se, assim, fundamental para o desenvolvimento tecnológico e aproveitamento
energético da biomassa. Esse estudo não poderá, contudo, ser feito nos queimadores
industriais, dado o seu alto custo em termos de potência de combustão. Há no entanto estudos
já feitos por Kaferstein (1997) com linhite, carvão e biomassa, tendo em atenção aspectos
ligados com a cinética das reacções, bem como a análise de componentes gasosos emitidos.
Nesses estudos, os ensaios experimentais foram conduzidos em duas câmaras de combustão
de leitos fluidizados de pequena escala. Um deles, em que se pretendeu estudar a cinética da
reacção, foi uma caldeira de leito fluidizado borbulhante (B.F.B.C.) de 15 kW de potência. O
outro foi uma caldeira de leito fluidizado circulante (C.F.B.C.) de potência 60 kW, onde se
pretendeu analisar os componentes gasosos emitidos.
A temperatura das caldeiras e fornalhas é controlada essencialmente pela transferência
de calor para as superfícies não refractárias, sejam elas parede de membrana ou feixe tubular,
no caminho do escoamento gasoso. Pode também ser controlada pelo uso de permutadores de
calor na conduta de recuperação de sólidos. Assim, é da maior importância a compreensão
dos fenómenos envolvidos na transferência de calor entre o leito e as superfícies de contacto e
nomeadamente com as paredes de membrana. Grande parte dos resultados experimentais,
como por exemplo os apresentados por Breitholtz (2000a), referem-se a leitos à escala
laboratorial ou a modelos em escala reduzida de caldeiras existentes, tendo em atenção a
igualdade de determinados grupos adimensionais. Os resultados obtidos pelas diferentes
equipas têm sido concordantes entre si, mas aparecem discrepâncias quando comparados com
os valores correspondentes às caldeiras reais. Para atenuar estas diferenças constatadas,
Breitholtz (2000b) e Basu (1996) entre outros, apresentam também estudos experimentais
feitos em caldeiras reais que trabalham na gama de 12 a 300 MW pretendendo com isso
determinar correlações para coeficientes de transferência de calor entre os leitos fluidizados e
as paredes das câmaras de combustão. Estas discrepâncias são devidas, essencialmente, à falta
de conhecimentos sobre a dinâmica de fluidos numa caldeira real. Segundo Breitholtz (1997)
há parâmetros como:
- a espessura de gás entre parede e partícula em suspensão;
- o tempo de residência das partículas;
2
1. Introdução
- a concentração de partículas ao longo da coluna;
- o movimento das partículas em direcção à parede.
que não são muito bem conhecidos e que devem continuar a fazer parte dos estudos em
trabalhos futuros. Além disso, o facto de muito dos dados experimentais em condições
laboratoriais serem obtidos a frio (temperaturas < 200 ºC) leva também a que apareçam
diferenças, quando estes são comparados com os obtidos nas câmaras de combustão a quente.
De acordo com o proposto por Breitholtz (1997), uma maneira de tentar atenuar essas
diferenças encontradas é introduzir parâmetros de compensação, para levar em consideração a
variação das propriedades do gás com a temperatura, bem como o efeito da componente de
radiação na transferência de calor, que nos ensaios laboratoriais a frio não tem qualquer
significado.
De acordo com informação recolhida, verificou-se que existiam muitos mais estudos de
transferência de calor em leitos fluidizados circulantes, quer à escala laboratorial quer em
caldeiras industriais, do que para leitos borbulhantes. Wen-Ching (2003) refere muitos
estudos de transferência de calor, em leitos fluidizados à escala laboratorial, feitos por
diversos autores, nomeadamente Biyikli et al (1983), que confirma a pouca informação
existente para a determinação de coeficientes de transferência de calor na zona de transporte
de leitos borbulhantes. Mesmo para leitos borbulhantes em larga escala não aparece
informação disponível já que segundo Johnsson (2000) este tipo de estudos acarreta altos
custos quando aplicado em leitos à escala industrial.
Além disso, os estudos de transferência de calor encontrados para leitos fluidizados
referem-se em geral a condições operatórias diferentes das que irão ser aqui desenvolvidas.
De acordo com Al-Busoul (2002) é feito um estudo usando superfícies imersas no próprio
leito. Também aparecem muitos estudos em que se considera o permutador de parede de
membrana confinado à zona do leito. Há no entanto um trabalho apresentado por Pagliuso
(2000), que apresenta resultados experimentais numa instalação muito próxima da que aqui
vai ser usada e que serviu de base para o projecto preliminar. No entanto este autor trabalha
com temperaturas da ordem dos 150 ºC e em condições de leito fluidizado circulante.
Face a tudo o que foi exposto, parece ser pertinente o estudo da transferência de calor na
zona acima da superfície livre de um leito fluidizado borbulhante, até porque a grande taxa de
transferência de calor que se observa deve-se sobretudo ao fenómeno de borbulhamento e
consequente projecção e espalhamento das partículas constituintes do leito para cima e para
fora deste. No entanto esse mesmo fenómeno também provoca a existência de caminhos
preferenciais para o gás e um contacto mais pobre entre gás e sólido devido à própria
3
1. Introdução
aglomeração de partículas. Isto significa que o grau de borbulhamento atingido no leito e
portanto a sua própria hidrodinâmica irá, certamente, influenciar a taxa de transferência de
calor das partículas para um permutador de parede de membrana. Além disso, e para que
todos os mecanismos associados à transferência de calor possam ser devidamente avaliados,
os ensaios serão conduzidos a quente ou seja a temperaturas superiores a 400ºC. Deste modo,
a influência da temperatura nas propriedades dos gases, bem como a transferência de calor por
radiação podem ser bem avaliadas. Por outro lado, também se farão estudos de transferência
de calor na presença de uma reacção de combustão.
Segundo Kunii e Levenspiel (1991), é evidente que o uso de um reactor em leito
fluidizado à escala laboratorial é em si uma limitação dadas as condicionantes que envolvem
sempre a interpretação dos fenómenos de transferência, quando se passa de uma escala tão
reduzida para uma escala industrial, mas tal é uma limitação inerente aos condicionalismos
económicos e consequentemente físicos impostos ao estudo.
1.2 Caracterização hidrodinâmica de um leito fluidizado.
Quando um fluido (líquido ou gás) passa através de uma coluna onde existe um leito de
partículas assente numa placa distribuidora, o leito começa por ser fixo, mas com o aumento
gradual do caudal de fluido dá-se o início da fluidização. Enquanto o leito está fixo as
partículas mantém-se paradas e o fluido apenas ocupa os espaços vazios existentes. Com o
aumento do caudal o leito vai-se expandindo, aumentando a sua porosidade reagindo assim ao
aumento do atrito entre partículas e fluido. O início da fluidização dá-se então quando as
partículas são suportadas pela corrente de fluido, e a queda de pressão nesse leito, dito
fluidizado, é igual ao peso aparente das partículas.
Nos sistemas gás-sólido, um aumento de caudal acima da fluidização incipiente leva a
grandes perturbações e instabilidades no leito. Há formação de grandes bolhas resultantes do
excesso de gás relativamente ao necessário à fluidização; bolhas essas que se podem agregar,
ocupando muitas vezes a quase totalidade do diâmetro do leito. Criam-se também caminhos
preferenciais para o escoamento do gás, e a altura do leito relativamente às condições de
fluidização mínima aumenta pouco. As partículas finas (vT < v0) escoam através do leito
descendo junto à parede e à volta das bolhas de gás. As partículas mais grossas (vT > v0) são
arrastadas pelas bolhas que rebentam à superfície mas acabam por cair, gerando assim
grandes instabilidades no leito como já foi referido.
4
1. Introdução
À medida que o caudal aumenta a superfície do leito deixa de ser perfeitamente definida
e em vez de bolhas observam-se movimentos turbulentos de agregados de partículas e espaços
vazios de várias formas e tamanhos que correspondem ao gás. Segundo Rhodes (1989), nesta
fase está-se na situação de fluidização turbulenta ou rápida. Neste regime não há choques
entre partículas, e o sistema é praticamente insensível à variação da velocidade do gás e ao
fluxo de sólidos imposto. De acordo com o mesmo autor, a região que fica compreendida
entre a superfície do leito fluidizado turbulento e a saída do gás é designada por zona de
transporte e pode ser por sua vez dividida em várias zonas:
zona de espalhamento - zona imediatamente acima da superfície do leito para a qual
são levadas as partículas mais grossas devido à erupção das bolhas que aí ocorre.
Essas partículas mais grossas voltam para trás descendo junto à parede; é uma zona
de grande agitação;
zona de desagregação - situa-se acima da zona anterior. Caracteriza-se pelo facto do
fluxo ascendente e da concentração da suspensão de partículas finas diminuir com a
altura. A altura desta zona, que é em geral medida a partir da superfície do leito, é
designada por “Transport Disengagement Height” (TDH). Existem correlações
empíricas para determinar o valor de TDH e uma das mais usadas é a equação de
Horio et al (1980) apresentada por Kunii e Levenspiel (1991), que foi a utilizada
neste trabalho e que serviu para o projecto preliminar da instalação experimental. A
partir do valor de TDH a concentração de partículas é constante, e a saída de gás da
coluna de fluidização deve situar-se acima deste valor;
zona de transporte em fase diluída - nesta zona grande parte das partículas é
arrastada pela corrente de fluido e o fluxo de partículas e a concentração da
suspensão é constante com a altura. Assim, as partículas terão de ser recolhidas por
um ou mais ciclones donde serão novamente introduzidas na coluna.
É este ciclo formado pela constante saída e entrada de partículas na coluna que constitui
um leito fluidizado circulante designado por C.F.B. Quando a velocidade superficial do gás
não é suficiente para provocar o arrasto das partículas acima da zona de desagregação então
não existe a zona de transporte em fase diluída e todos os sólidos retornam ao leito, podendo,
no entanto, existir algum transporte apenas das partículas mais finas mas que não terá
qualquer significado. Neste caso está-se perante um leito borbulhante, designado na literatura
científica como B.F.B.
5
1. Introdução
A Figura 1.1 que se apresenta de seguida pretende mostrar as várias zonas referidas
atrás.
Altura acima
do distribuidor
Fase diluída
Zona de Transporte
Altura de desagregação
(TDH)
Zona de espalhamento
leito
Densidade da suspensão
Figura 1.1- Zonas características de um leito fluidizado, Rhodes (1998).
Há vantagens e desvantagens de um tipo de leito relativamente ao outro, mas em termos
laboratoriais é vantajoso o uso de leitos borbulhantes em alternativa aos circulantes. As
desvantagens principais que se podem enumerar no caso de leitos circulantes à escala
laboratorial são:
- colunas muito altas;
- grande desgaste da parede da coluna;
- impossibilidade do uso de anteparos ou de superfícies de transferência de
calor interiores, devido ao desgaste permanente por causa do atrito;
- perda de partículas devido ao arrasto;
- necessidade de altas potências de aquecimento para os altos caudais de gás a
que obriga a manutenção dos leitos circulantes.
1.2.1 Classificação de partículas
A hidrodinâmica de um leito fluidizado é também influenciada pelo tipo de partículas
que constitui o enchimento da coluna. Geldart (1986), apresenta um trabalho referente a uma
classificação de partículas em função das suas propriedades físicas, que permite dividi-las em
grupos de acordo com o seu comportamento num leito fluidizado. Esse mapa é apresentado na
Figura 1.2 que se segue.
6
1. Introdução
Figura 1.2- Classificação das partículas segundo Geldart, para fluidização com ar à temperatura
ambiente e para v0< 10vmf , Geldart (1986)
Os grupos mencionados na Figura 1.2 apresentam as seguintes características:
- Grupo A – partículas porosas ou materiais formados por partículas de tamanho médio,
pequeno e/ou baixa massa volúmica (< 1,4 g/m3).Estes sólidos fluidizam
facilmente a baixas velocidades de gás e o borbulhamento é controlado já
que se formam pequenas bolhas mesmo a altas velocidade de gás;
- Grupo B – a maior parte das partículas têm diâmetro 40 <dp (µm)<500 e massa
volúmica 1,4 < ρs (g/cm3)< 4 como por exemplo a areia. Estes sólidos
fluidizam bem com muita agitação devido ao grande borbulhamento
conseguido.
- Grupo C – materiais formados por partículas com tendência para uma grande coesão,
pelo facto de serem muito finas. A fluidização normal é extremamente
difícil devido à grande intensidade das forças inter-particulares
relativamente às forças resultantes da acção do gás.
- Grupo D – materiais formados por partículas grandes e/ou densas. São também de
difícil fluidização. Dão origem a grandes bolhas e originam caminhos
preferenciais para o gás sendo a distribuição de gás no leito muito pouco
uniforme.
De acordo com a Figura 1.2, conhecendo a massa volúmica do material e o diâmetro
médio das partículas que o constituem pode-se logo prever o tipo de fluidização que será
esperada de acordo com o tipo de partículas que se tem.
7
1. Introdução
De acordo com Kunii e Levenspiel (1991), apesar da areia usada neste trabalho estar
incluída no grupo B desta classificação, as condições de trabalho a quente e as velocidades
superficiais usadas podem levar a que as partículas classificadas como do tipo B se
comportem como partículas do tipo A.
Segundo Gupta (2000), os reactores de “cracking” catalítico que usam leitos fluidizados
circulantes empregam, em geral, partículas do grupo A segundo esta classificação de Geldart,
e operam com altas taxas de circulação de sólidos e altas velocidades de gás, enquanto que as
câmaras de combustão operam com sólidos do grupo B e a velocidades de gás mais baixas.
1.2.2 Modelo do Anel
Vários autores, como por exemplo Sundersan (2001) e Wang (1995), a partir de vários
estudos e observações experimentais, compararam a zona de transporte em leitos fluidizados
circulantes a uma estrutura núcleo-anel na direcção radial. Este modelo caracteriza-se por
uma zona central diluída (zona do núcleo), onde as partículas são transportadas para cima, e
uma zona densa junto às paredes do leito que é formada pelas partículas que caem ao longo da
coluna.
Para a temperatura ambiente, a espessura da camada de partículas que desce junto à
parede é praticamente independente do fluxo de sólidos imposto. Para temperaturas mais
elevadas as características hidrodinâmicas do leito são alteradas sobretudo por via das
propriedades do gás (densidade e viscosidade). Também a massa específica da suspensão
diminui com o aumento da temperatura, o que influencia a hidrodinâmica do leito.
De acordo com este modelo do anel, Wen (1982) fez estudos para analisar o movimento
das partículas da fase diluída que foram lançadas para essa zona a partir da superfície do leito,
devido às bolhas que aí chegaram. Esse movimento de partículas acima da zona borbulhante
pode ser determinado em termos de parâmetros hidrodinâmicos como:
- excesso de gás acima do necessário à fluidização, (v0-vmf);
- diâmetro da coluna.
Este autor verificou também que o arrasto dessas partículas, a partir da superfície do
leito, diminui exponencialmente ao longo da zona de transporte, e, são essas que vão
descendo junto à parede, que vão formar a zona densa. No entanto uma pequena quantidade
de partículas mais finas, cuja velocidade terminal seja menor que a velocidade superficial do
gás, podem sair juntamente com o gás e nesse caso devem ser recolhidas em ciclones para
8
1. Introdução
retornarem de novo ao leito. Isto pode ser devido a dois factores: a altura da zona de
transporte não é suficientemente alta para que as partículas retornem ao leito; o gás escoa por
caminhos preferenciais onde apresenta grandes velocidades locais.
A transferência de calor do leito para a parede vai ser sobretudo dependente da
hidrodinâmica do escoamento nessa zona e das propriedades físicas do gás. A componente de
radiação, que começa a ser importante a partir de temperaturas superiores a 600 ºC, vai
também depender da densidade da suspensão na zona densa, junto à parede. Se a densidade da
suspensão aumenta, a transferência de calor por radiação diminui, devido ao efeito de escudo
de radiação causado pelas partículas que caem junto à parede.
1.2.3 Determinação da fracção volumétrica local de sólidos
Um dos parâmetros essenciais à determinação da taxa de transferência de calor, devido à
convecção das partículas em leitos fluidizados a alta temperatura, é a determinação local da
fracção volumétrica de sólidos. Segundo Johnsson (2001), um dos métodos mais indicados
para este efeito é um método óptico. O método mais comum é a determinação da queda de
pressão ao longo da zona de transporte, mas não permite avaliar a fracção volumétrica local
de sólidos nem a sua variação com o tempo.
No método óptico usam-se sondas ópticas formadas por duas fibras, sendo uma exposta
às partículas e outra que recebe a luz reflectida por essas mesmas partículas. Este autor fez
ensaios em leitos fluidizados electricamente aquecidos sem combustão, em leitos circulantes e
ainda em câmaras de combustão de leitos circulantes. No primeiro caso, verificou que a sonda
era capaz de detectar a presença de bolhas até à temperatura de 800 ºC, que foi a temperatura
máxima de operação. Assim, pôde detectar que o fluxo de sólidos que descia junto à parede
consistia numa nuvem de partículas em que a fracção volumétrica de sólidos não era
uniforme. No entanto, na presença de combustão, o método era difícil de aplicar porque
interferia no próprio leito e a combustão era ela própria uma fonte de luz. Isto obriga a que os
sistemas de detecção tenham de ser protegidos no caso de temperaturas superiores a 850 ºC.
No presente trabalho apenas se usou a medição da perda de carga ao longo do
escoamento gasoso, para detecção da existência ou não de partículas nessa zona.
9
1. Introdução
1.3 Modelos desenvolvidos para estimar coeficientes de transferência de calor acima dos
leitos fluidizados.
Como já foi referido, encontrou-se muito pouco trabalho científico na área de
transferência de calor na zona acima dos leitos fluidizados borbulhantes, embora haja bastante
literatura publicada para o estudo da cinética das reacções que podem ocorrer nesse tipo de
leitos. No entanto, no caso de leitos circulantes, em que o fenómeno principal na transferência
de calor diz respeito ao borbulhamento, encontraram-se bastantes trabalhos científicos
relativamente a estudos de transferência de calor. Nesta situação, vários modelos foram
encontrados para determinação de coeficientes globais de transferência de calor sob a forma
adimensional em termos do número de Nusselt. Muitos desses modelos serviram de base para
todo o desenvolvimento feito neste trabalho, com as limitações decorrentes de uma medição
experimental inovadora na área de leitos borbulhantes e com condições operatórias também
diferentes, sobretudo no que diz respeito às temperaturas de operação elevadas com que se
trabalhou. Embora nos leitos fluidizados circulantes típicos a transferência de calor ocorra a
temperaturas elevadas, existem poucos dados recolhidos a essas temperaturas e, quando
comparados com os muitos que existem à temperatura ambiente, nem sempre permitem
revelar a importância da radiação.
Wirth (1995), apresenta um modelo para determinação do coeficiente global de
transferência de calor em leitos fluidizados circulantes expresso em termos de grupos
adimensionais como: o número de Arquimedes que caracteriza o escoamento gás–sólido junto
à parede; e o número de queda de pressão definido como ∆p/((ρp-ρg)(1-εmf)ghL)), que
relaciona a concentração de sólidos numa dada secção recta da coluna com a concentração de
sólidos nas condições de fluidização mínima. Este autor compara medidas experimentais
obtidas em duas unidades (uma a quente e outra a frio) e verifica que, com o aumento do
número de queda de pressão, o número de Nusselt nas duas unidades se aproxima, o que
significa que a radiação deixa de ser o principal mecanismo de transferência de calor. Isto
acontece devido ao efeito do escudo de radiação causado pela maior concentração de
partículas junto à parede. O valor do número de Arquimedes está relacionado com os
mecanismos de condução e convecção: valores baixos deste parâmetro significam que a
condução através do gás é o mecanismo fundamental; enquanto que para valores altos do
número de Arquimedes os efeitos de convecção devido ao gás passam a ser mais importantes.
10
1. Introdução
Um outro autor, Subbarao (1986), acrescenta algum saber ao estudo do fenómeno de
borbulhamento em leitos fluidizados circulantes já que é esse fenómeno o responsável pelas
altas taxas de transferência de calor que se verificam. Nestes estudos, Subbarao conclui que o
coeficiente de transferência de calor deve ser calculado como a soma de duas contribuições, já
que da fluidização turbulenta fazem parte as bolhas de gás e as partículas que têm tendência a
a agregarem-se e a formarem “nuvens de partículas”. Se a área de transferência de calor for
unitária, então existe uma parte dessa área que está exposta às nuvens de partículas e a
restante estará exposta às bolhas. Deste modo, o coeficiente de transferência de calor será
calculado como uma média ponderada destas duas contribuições. Acrescenta também uma
variável importante neste estudo, que é o tempo de contacto entre as nuvens de partículas e a
fracção da parede com a qual contactam, e também o tempo de contacto entre as bolhas e a
mesma fracção de parede. Durante esse período, a transferência de calor ocorre em estado
transiente. Basu (1997) baseia-se também neste modelo e analisa o efeito do tamanho das
partículas e da temperatura do leito na taxa de transferência de calor.
Noymer (1999) desenvolveu uma nova técnica chamada TIV, “Thermal Image
Velocimetry”, que consistia em aquecer os agregados de partículas que se deslocavam junto à
parede, e usando a sua energia radiante podia distingui-los do resto do leito por uma câmara
de infravermelhos. A velocidade média das nuvens de partículas foi entre 1,1 a 1,2 m/s e
mostrou pouca dependência das condições de operação. Os tempos de residência encontrados
situaram-se na gama de 0,15 a 0,5 s, e mostraram ser dependentes da densidade dos sólidos.
Os modelos desenvolvidos permitem estimar a força de arrasto, paralela à parede, e a força
que afasta os agregados da parede, perpendicular à parede.
Estas determinações experimentais são aplicadas aos modelos de transferência de calor
desenvolvidos por outros autores que, além de desprezarem a radiação, consideram a
convecção do gás e a condução transiente das partículas (também referida como convecção
pelas partículas) como efeitos em paralelo. Então a parede é coberta quer pelo gás quer pelos
agregados de partículas. A convecção pelas partículas consiste na troca de energia por
condução transiente entre as nuvens e a parede e o contacto imperfeito resulta numa
resistência adicional de contacto. A convecção pelo gás pode ser estimada usando correlações
correspondentes a uma única fase gasosa.
Al–Busoul (2002), em estudos referentes à transferência de calor em leitos fluidizados
com superfícies imersas, considera que o coeficiente global de transferência de calor pode ser
visto como a soma de três parcelas: a contribuição convectiva do gás, hgc, a contribuição da
radiação, hrad, e a contribuição devida ao movimento das partículas, hpc. Desta forma, o fluxo
11
1. Introdução
de calor da superfície imersa para o leito é calculado como o produto desse coeficiente global
pela diferença de temperatura entre a superfície imersa e o leito, podendo também ser
calculado à custa de hpc se for conhecida a temperatura das partículas, que em estado
estacionário pode ser assumida como a temperatura do leito. Este mesmo autor propõe
correlações para o cálculo de cada um dos coeficientes referidos acima. O valor de hgc pode
ser estimado à custa de correlações existentes para gás a escoar, através de uma coluna vazia,
à mesma velocidade e usando as propriedades do gás. A componente de radiação,
correspondente a hrad, que será desprezável para temperaturas inferiores a 600 ºC, mas
importante a temperaturas mais altas e sobretudo em leitos de baixa densidade, é calculada
considerando o leito como um corpo cinzento e o modelo de radiação que aqui se considera
trata a superfície e o leito como placas paralelas com a mesma área. Para o cálculo de hpc este
autor chega a uma correlação a partir de um balanço de energia a uma partícula que se move
irregularmente através do leito e que troca calor com a superfície na vizinhança da parede.
Foi com base neste critério, apresentado por Al–Busoul (2002) e por outros autores,
nomeadamente Bi and Grace (2000), Sundaresan (2002) e Wu (1989), relativo à contribuição
aditiva dos diversos mecanismos de transferência de calor, que se partiu para fazer, no
presente trabalho, uma análise quantitativa desses mesmos mecanismos. Se para o cálculo de
hgc se seguiu a metodologia adoptada por Al–Busoul (2002), já para o cálculo dos outos dois
coeficientes o processo foi diferente, como adiante se explicará.
1.4 Influência de diferentes parâmetros na transferência de calor
Foi também feita uma pesquisa bibliográfica relativamente à influência de diferentes
parâmetros na transferência de calor em leitos fluidizados. De acordo com o trabalho
experimental desenvolvido por Pagliuso (2000), feito numa instalação com uma série de
permutadores de parede de membrana com dimensões próximas das usadas neste trabalho, as
conclusões foram as seguintes:
- Densidade da suspensão: é um dos parâmetros mais importantes que determina a
transferência de calor para a parede. Quando a densidade da suspensão aumenta, o coeficiente
de convecção também aumenta, devido ao movimento das partículas;
- Taxa de circulação de sólidos: verificou-se experimentalmente que este parâmetro
afecta mais o valor do coeficiente de transferência de calor do que o diâmetro das partículas.
12
1. Introdução
Isto acontece porque o fluxo de circulação de sólidos é directamente proporcional à densidade
da suspensão e inversamente proporcional ao diâmetro das partículas;
- Superfície de transferência de calor: no trabalho experimental deste autor, verificou-se
que não há praticamente influência da extensão desta superfície no valor do coeficiente de
transferência de calor, para o caso de comprimentos maiores do que 0,93 m, que foram os
testados. Por outro lado, como as superfícies de transferência de calor são paredes de
membrana, os coeficientes do lado da água são em geral muito maiores do que os do lado do
leito, e por isso o coeficiente global é pouco afectado pelo caudal de água;
- Tamanho das partículas: o diâmetro das partículas é também um parâmetro importante
para o estudo da transferência de calor em leitos fluidizados, verificando-se que, para a
mesma densidade de suspensão, as partículas mais pequenas permitem obter coeficientes
maiores do que as partículas maiores. Wu (1987) verificou também que o efeito do tamanho
das partículas era mais evidente em superfícies de transferência de calor com altura de 0,3 m
do que em superfícies de altura 1,53 m;
- Velocidade superficial do gás: com o aumento da velocidade superficial do gás, a
concentração de sólidos no leito diminui e por isso o coeficiente de transferência de calor
baixa, donde se conclui que a maior contribuição para a transferência de calor é dada pela
convecção das partículas. Assim, no caso de densidade de suspensão constante, a velocidade
superficial do gás pouco influencia o valor do coeficiente de transferência de calor, o que
mais uma vez comprova a pouca importância da convecção por parte do gás;
- Temperatura média do leito: o coeficiente de transferência de calor aumenta com a
temperatura média da suspensão devido, quer ao aumento da condutibilidade térmica do gás,
quer ao efeito da radiação. Para temperaturas maiores que 500ºC e sobretudo para leitos diluídos
(ρsus<15 kg/m3), onde a radiação é o processo dominante na transferência de calor, o aumento da
transferência de calor com o aumento da temperatura pode ser muito significativo;
- Pressão: o aumento da pressão provoca um aumento do coeficiente de transferência de
calor, para uma dada densidade da suspensão. Este efeito é menor para partículas mais pequenas.
1.5 Reactores de leitos fluidizados
Não foi encontrada informação sobre o estudo de transferência de calor em processos que
envolvessem a queima específica do propano em leitos fluidizados, mas encontraram-se
trabalhos feitos por diversos autores nomeadamente, Gayan (2004), Dounit (2001), Ribeiro
13
1. Introdução
(2002) e Ribeiro e Pinho (2004), que procuraram, através de ensaios experimentais, estudar a
eficiência de reacções de combustão em câmaras de leitos fluidizados, preocupando-se mais com
a cinética das respectivas reacções do que com a taxa de transferência de calor. O primeiro autor
referido estudou a queima de biomassa, carvões de baixa qualidade e resíduos orgânicos, em
câmaras de combustão de leitos fluidizados circulantes. Dounit (2001) procurou estudar a
cinética das reacções e também a transferência de calor resultante da combustão de gás natural
com ar em leitos fluidizados; usou apenas uma granulometria de areia de 350 µm e trabalhou em
condições de excesso de ar. Ribeiro e Pinho (2004) apresentaram neste trabalho estudos
experimentais correspondentes à combustão de propano em leitos fluidizados, em condições de
excesso de ar, mas usando várias granulometrias de areia entre 200 e 500 µm.
Nos trabalhos de Dounit (2001), a temperatura dos ensaios situou-se entre 600 e 850 ºC.
Este autor, que estudou a combustão do gás natural, fez ensaios laboratoriais que permitiram
medir quer a concentração de metano na zona de projecção de sólidos, quer a temperatura dos
gases na zona de transporte, dando assim destaque à existência de uma temperatura crítica do
leito na gama de 750 a 800 ºC, para a qual a mistura gasosa é queimada dentro do leito.
Verificou também, pelos resultados obtidos, que a zona de projecção de sólidos tem uma
importância fundamental na eficiência térmica da reacção de combustão e, abaixo de 850 ºC, a
maior parte da reacção de combustão ocorre nessa zona. Pela avaliação da evolução da
temperatura dos gases ao longo do reactor, pode ser determinada a zona onde se está a processar
a reacção de combustão, pois essa zona corresponde a um pico na temperatura do leito. Para
temperaturas do leito crescentes a zona de reacção afasta-se da superfície do leito, e para
temperaturas do leito maiores que 850 º C a combustão tem lugar no interior do próprio leito.
Paralelamente, este autor propõe um modelo para a reacção de combustão metano-ar que
tem em consideração vários factores: a interacção entre as duas fases do leito, fase densa e fase
diluída, a variação do caudal de gás ao longo do leito e a transferência de calor, quer por
condução, quer por radiação, entre a fase gasosa e a fase densa, e entre a suspensão das
partículas e as paredes do reactor. Assim, para equacionar o modelo proposto por este autor, foi
necessário ter em consideração as seguintes variáveis:
- variação da densidade da suspensão;
- o arrasto das partículas ao longo da zona de transporte que decresce exponencialmente a
partir da superfície do leito;
- o fluxo de partículas à superfície do leito;
- a cinética das reacções químicas respectivas;
14
1. Introdução
- um factor de eficiência de contacto, devido à natureza da projecção das partículas, que
leva a que apenas uma fracção da superfície total disponível seja acessível ao gás.
Nos trabalhos apresentados por Ribeiro (2002) e Ribeiro e Pinho (2004) também se
conclui que a temperatura do leito é um critério que evidencia a progressão da reacção. As
próprias explosões que ocorrem, características das reacções de combustão, podem, segundo
este autor, ocorrer dentro do próprio leito, tornando-se pouco perceptíveis, ou acima da
superfície do mesmo, dependendo da sua temperatura. Também verificou que, à medida que a
temperatura do leito aumentava, a reacção de combustão tendia a dar-se no interior do leito,
deslocando-se para a superfície, à medida que a temperatura baixava.
Refere-se, mais uma vez, que a determinação de coeficientes de transferência de calor,
em simultâneo com a realização de reacções de combustão, não aparece na literatura, à
excepção do trabalho de Dounit (2001).
15
2.Projecto da instalação experimental
2.Projecto da instalação experimental
2.1 Definição das condições de operação pretendidas, de acordo com os objectivos
propostos, materiais a usar e sua caracterização.
Como já foi referido, o estudo de sistemas de queima adequados às novas limitações
ambientais e a utilização de fontes de energia renováveis, como a biomassa, têm vindo a
ganhar cada vez mais importância, quer junto da comunidade Científica, quer a nível político.
O leito fluidizado é uma tecnologia já bem estabelecida, com boas provas dadas em
termos de controlo das emissões de poluentes gasosos e que, ao mesmo tempo, se tem
revelado adequada à queima de biomassa. Existem de uma forma geral dois tipos de leitos: o
leito fluidizado borbulhante e o leito fluidizado circulante.
Dada a energia consumida para manter o leito fluidizado, para instalações de pequena
potência e até 1 MW, utilizam-se preferencialmente queimadores de grelha fixa; de 1 MW até
10 MW, e segundo Obernberger (1998), passam a ser dominantes os queimadores de grelha
variável.
À medida que a potência térmica debitada na combustão cresce, os leitos fluidizados
borbulhantes começam a ter aplicação prática. Acima de 10 MW e até 30 MW, os leitos
fluidizados borbulhantes, e segundo o mesmo autor, são os que têm a gama de utilização
ideal, enquanto que acima dos 30 MW são os leitos fluidizados circulantes os mais indicados.
Como interessava ter uma instalação laboratorial polivalente, que pudesse funcionar tanto em
regime borbulhante como circulante, optou-se por uma concepção híbrida.
Pretendeu-se então, numa primeira fase deste trabalho, projectar uma instalação de leito
fluidizado com grelha fixa à escala laboratorial, com uma parede de membrana, tentando-se
simular o melhor possível a situação das caldeiras reais em que o calor está a ser transferido
17
2.Projecto da instalação experimental
da suspensão para as paredes de membrana, em vez de se usarem provetes aquecidos e de se
medir o calor que passa destes para a suspensão.
O combustível a usar será o propano comercial, o enchimento do leito será areia de
sílica, e toda a coluna será feita em aço inox. Inicialmente, pensou-se impor como potência
térmica máxima 50 kW, mas rapidamente se concluiu que este valor era demasiado ousado
para o espaço físico disponível, para os gastos de água e combustíveis envolvidos e, ainda,
para as condições de segurança que se exigiam.
Uma vez que os gases foram admitidos frios na coluna, foi necessário envolver a parte
de baixo do reactor com uma resistência eléctrica de 2000 W, que foi inserida dentro de
tijolos refractários permitindo atingir as condições de temperatura necessárias à auto-ignição
do propano. Só para temperaturas acima de 700–720ºC irá ser feita a alimentação do propano,
dando-se assim início à reacção de combustão. Para diminuir as perdas de calor para o
exterior, toda a câmara de combustão, bem como todo o leito, foi envolvido em lã cerâmica,
da marca “Kawool”.
As condições de trabalho previstas, os materiais a usar e os cálculos necessários para o
projecto desta coluna, foram os seguintes:
- Pressão de operação - 1atm;
- Material a usar na construção da coluna – aço inox;
- Material para o enchimento do leito - areia de sílica: é feita a caracterização prévia da
areia a usar relativamente ao tamanho das partículas, à sua massa volúmica e à sua
porosidade, nas condições mínimas de fluidização;
- Combustível a usar : gás propano comercial;
- Temperatura de arranque para alimentação do combustível deverá variar entre 700 e
720 ºC ( para que seja possível a auto-ignição do propano );
- Altura do leito de areia entre 100 a 200 mm;
- Tendo como base o trabalho desenvolvido por Pagliuso (2000), fixou-se o diâmetro da
coluna em 50 mm, sendo esta constituída por dois permutadores de duplo tubo com
cerca de 1 m de altura em cada um. O espaçamento entre os dois tubos concêntricos será
de cerca de 10 mm;
- Foi necessária uma primeira estimativa da velocidade superficial do ar a circular na
coluna para estabelecimento das condições de fluidização rápida –“Fast Fluidization”.
18
2.Projecto da instalação experimental
Numa primeira análise, e depois de alguma pesquisa bibliográfica, chegou-se à
conclusão que, segundo Kunii e Levenspiel (1991), para garantir esse tipo de escoamento era
necessário que v0 >20 vt. No entanto, esta estimativa iria também depender da potência
térmica da instalação, que por sua vez condicionaria o caudal de água a circular no tubo
exterior do permutador e a respectiva variação de temperatura.
Para que se pudesse ter uma noção do caudal de ar necessário e, consequentemente, do
caudal de propano a queimar, tendo em atenção a estequiometria da reacção de queima, foi
calculada previamente a velocidade mínima de fluidização, vmf, e a velocidade terminal, vt,
para cada dimensão de areia. As correlações de vmf = f(T) e de vt = f(T) determinadas para
cada diâmetro de areia estão apresentadas no Apêndice I.
Só depois de terem sido feitos estes cálculos preliminares é que se pôde estimar o valor
requerido para a velocidade superficial do ar, e assim estimar também o caudal de propano, de
acordo com a estequiometria da reacção. Foi sempre preciso ter em atenção a potência térmica
que estas estimativas acarretavam, pois a resistência eléctrica de 2000 W foi uma limitação
física para o aquecimento necessário à auto-ignição do propano. Face aos resultados obtidos
poderia vir a ser necessário, aquando do arranque da instalação, fazer um ajuste do caudal de
ar a escoar.
A seguir foram projectados os medidores de orifício, cujas tomas de pressão são ligadas
a transdutores de pressão que vão permitir a sua calibração e assim estabelecer o caudal de ar
e propano a circular no leito.
Tendo em atenção as alturas definidas para a zona do leito, para os dois permutadores, o
espaço necessário para montar o distribuidor, e o tamanho do plenum para admissão dos
gases, a altura total da coluna foi de cerca de 2500 mm. Este valor, além de estar dentro dos
limites físicos do laboratório onde foi colocada a instalação, também está dentro dos limites
fixados pelo cálculo preliminar da variável TDH – altura de desagregação, que é medida
desde a superfície do leito até ao início da zona de Fase diluída. Acima deste valor, existe
transporte de sólidos a um fluxo constante. De acordo com Rhodes (1998) a saída do gás deve
situar-se acima do valor de TDH estimado.
O cálculo de TDH foi feito de acordo com a equação proposta por Horio et al (1980)
apresentada em Rhodes (1998),
0,5
TDH = 4, 47 d BVS
(2.1)
19
2.Projecto da instalação experimental
sendo preciso também estimar o valor do diâmetro equivalente das bolhas à superfície do
leito.
De acordo com o proposto por Darton et al (1977), apresentada em Rhodes (1998) para
partículas do grupo B, que é o caso das partículas usadas neste trabalho a correlação usada
para estimar dBVS foi:
d BVS = 0,54(v0 − vmf )0,4 (hL + 4 N − 0,5 )0,8
(2.2)
em que hL é a altura do leito, e N é o número de orifícios por unidade de área do distribuidor.
O valor da altura do leito fixou-se em 200 mm, o diâmetro interno da coluna já se
encontrava estabelecido como sendo 54,5 mm, a velocidade do ar para poder garantir
condições de fluidização rápida, será da ordem de vinte vezes a velocidade terminal das
partículas e se for estabelecido nor = 200 para o número de orifícios da placa distribuidora- ver
secção 2.2 - o valor obtido para TDH situa-se entre 2 e 2,5 m. Este valor está de acordo com a
altura já prevista para a coluna e também com a relação H/di encontrada em vários artigos
existentes, nomeadamente no artigo de Bai (1999), onde são apresentados valores de H e di
propostos pelo próprio autor e por outros (como por exemplo Horio et al (1988)).
Estando nesta primeira fase as dimensões da coluna projectadas foi necessário passar ao
projecto do distribuidor e do ciclone.
2.2 Projecto do distribuidor
O projecto do distribuidor foi feito de acordo com o método apresentado por Kunii e
Levenspiel (1991).
Segundo estes autores a queda de pressão no distribuidor deve permitir um escoamento
uniforme em toda a secção da coluna. Para que isso aconteça, é necessário que ∆Pd = 0,2 a 0,4
∆PL em condições de fluidização mínima. Devem-se no entanto usar valores maiores para se
poder trabalhar também em regime circulante. O valor obtido para a queda de pressão no leito
permitiu calcular o número de orifícios a fazer numa placa de chapa de aço inox\ que vai
constituir o distribuidor.
O processo de cálculo, segundo os mesmos autores envolveu os seguintes passos:
- calcular ∆Pmf;
- impor ∆Pd = 0,3 ∆Pmf ;
20
2.Projecto da instalação experimental
- corrigir a velocidade do gás no leito para as condições de temperatura e pressão no
distribuidor, de acordo com:
vo
co rr
TP
ρL
= vo d L
ρd
TL Pd
= vo
( 2.3)
- calcular o número de Reynolds baseado no diâmetro interno da coluna tendo em
atenção a correcção feita anteriormente (Re = div0corr ρg/µg);
- determinar o coeficiente do orifício de acordo com a tabela 2.1;
Tabela 2.1 Coeficiente do orifício em função do número de Reynolds (Kunii e Levenspiel
(1991))
Re
100
300
500
1000
2000
>3000
cdor
0.68
0.70
0.68
0.64
0.61
0.60
- determinar a velocidade do gás através do orifício,v0r :
 2∆P d
vor = cd or 
 ρg

1/ 2



(2.4)
em que ρg é calculado à pressão e temperatura do distribuidor (valor estimado);
- através de um balanço de massa tem-se que:
ρd
π di2
4
v0 corr = ρ d
π dor 2
4
n or vor
(2.5)
Então fixando o dor tendo em atenção o diâmetro das partículas a usar, pode ser
estimado o número de orifícios, nor, a fazer na placa distribuidora. Como primeira estimativa
considerou-se dor = 3,5x10-4 m e o resultado obtido foi de 200 orifícios.
O problema que se pôs posteriormente foi o da possibilidade de fazer furos da dimensão
desejada numa chapa de aço inox. Face à não exequibilidade da perfuração pretendida
repetiram-se os cálculos assumindo a menor perfuração possível, e o nor a fazer situou-se na
ordem dos 100. O valor para dor foi de 1,5 mm mas como este valor é muito superior à
dimensão média das partículas, houve necessidade de fazer duas placas com a mesma
perfuração e colocar entre elas uma película de um material resistente a altas temperaturas.
21
2.Projecto da instalação experimental
Deste modo garantia-se que as partículas de areia não caíssem e se mantivessem acima da
placa do distribuidor.
Ao fim de alguns ensaios houve problemas na combustão do propano e o distribuidor foi
desmontado e verificou-se que a película usada estava completamente destruída. Este
fenómeno deve ter sido uma consequência não da alta temperatura a que foram feitos os
ensaios, mas da erosão provocada pela areia que se foi acumulando entre as duas chapas junto
à película.
Fez-se então um novo distribuidor usando apenas uma chapa de aço com uma matriz de
10x10 furos conseguindo-se uma perfuração ligeiramente mais pequena, ou seja dor = 0,6 mm.
Com a continuação dos ensaios a areia teve tendência a cair e a passar para o plenum
pelo que foi necessário fazer limpezas periódicas, pois a areia aí acumulada tinha implicações
na entrada dos gases e na combustão do propano. Uma técnica usada para minimizar a
passagem da areia pelos furos do distribuidor, foi a de se manter o leito permanentemente
fluidizado.
2.3 Projecto do ciclone
Depois de se terem definido limites para o caudal de gás a escoar ao longo da coluna
tendo em consideração parâmetros já apresentados como: velocidade mínima de fluidização,
velocidade terminal das partículas, condições necessárias à circulação de sólidos -“Fast
Fluidization”- e ainda a estequiometria da reacção da queima do propano, as dimensões do
ciclone foram definidas através de um método empírico-método proposto por Macintyre
(1988).
No método referido começa-se por calcular o diâmetro do ciclone- Dcicl - consoante se
opta por um separador de alto ou médio rendimento. Se a opção for a de alto rendimento a
expressão a usar é:
Qar= 1,524 Dcicl2
(2.6)
Depois de definido o diâmetro do ciclone, as outras dimensões de projecto são apresentadas
na Tabela 2.2:
22
2.Projecto da instalação experimental
Tabela 2.2 Parâmetros para projecto do ciclone, Macintyre (1988)
Dimensões
Factor
Dcicl
Ac
Sc
De
Lc
Zc
1
0,5
0,5
0,5
1,5
2,5
multiplicativo
Em que cada uma das siglas usadas se referem às dimensões apresentadas na figura que
se segue.
Figura 2.1 Esquema de um separador ciclónico
As dimensões definidas permitem posteriormente estimar o diâmetro mínimo das
partículas a separar no ciclone com uma probabilidade de 100%, e usando a expressão
proposta por Macintyre (1988):
d min = d100 =
9 µ g Bc
π N e va ρ p
(2.7)
em que:
Bc=Dcicl/4;
Ne= nº de espirais( valor entre 5 e 10);
va – velocidade média na admissão do ciclone (va=Qar/Ac.Bc).
23
2.Projecto da instalação experimental
De acordo com as dimensões definidas obteve-se um diâmetro mínimo de partículas
inferior ao das partículas que se usaram. Assim sendo a separação será de 100%.
O mesmo autor apresenta uma equação simples para cálculo da queda de pressão no
ciclone:
∆p
cicl
=
31Lc H c
kD e 2 3
Lc
Dcicl
3
(2.8)
Zc
Dcicl
em que:
Hc= Lc+Zc
k=0.5 para entrada simples s/ guia
k=1 para entrada c/ guia recta
k=2 para entrada c/ guia expansora.
2.4 Projecto das placas de orifício para medição de caudais de gases
O propano entrou no “plenum” abaixo do distribuidor e o seu caudal foi controlado por
uma válvula agulha e medido através de uma placa de orifício cujo projecto se apresenta de
seguida.
O projecto das placas de orifício teve como base os caudais máximos e mínimo de ar e
de propano de acordo com condições estequiométricas, com as exigências do escoamento em
termos de transporte de sólidos e ainda com os limites da potência de aquecimento que se
instalou na coluna.
A equação de projecto para cada medidor de orifício é dada pela equação:
mg = cd or
2∆p ρ g
π d 02r
  d or 4 
1 −  d  
i  
 
4
γ
Os tubos usados foram todos de aço inox e as placas de chapa de latão.
Os resultados obtidos estão apresentados na tabela seguinte:
24
(2.9)
2.Projecto da instalação experimental
Tabela 2.3 Resultados obtidos para as duas placas de orifício
Diâmetro do
Gases
Diâmetro do tubo
Ar
3/8”
5
Propano
1/4”
1
orifício(mm)
Foram calibradas várias placas de orifício para diferentes pressões para se poder
escolher face ao comportamento no arranque da instalação, quais as mais adequadas. Poderia
haver necessidade de cobrir gamas de caudais diferentes, sobretudo nos ensaios com
combustão de propano. No Apêndice II são apresentadas todas as curvas de calibração obtidas
para diferentes placas de orifício e para diferentes valores de pressão, bem como as
respectivas incertezas. Para trabalho futuro pode ser útil trabalhar a caudais mais elevados e
ter então necessidade de usar uma entrada de ar primário e outra de ar secundário, bem como
caudais mais altos de propano.
As curvas de calibração que foram efectivamente usadas neste trabalho são apresentadas
neste mesmo Apêndice II.A correspondente ao propano aparece na Figura A.II.9 e a
correspondente ao ar aparece na Figura A.II.14.
2.5 Estimativa do caudal de água a circular na camisa
A gama de caudais a usar na camisa de arrefecimento foi determinada tendo em atenção
a potência térmica de trabalho e também variações de temperatura admissíveis no escoamento
da água.
Para os caudais assim obtidos, e também para assegurar uma leitura contínua através do
sistema de aquisição de dados pensou-se em escolher numa primeira fase, um debitómetro de
turbina para medição do caudal, cujo controlo era também assegurado por uma válvula de
agulha.
O debitómetro de turbina permite adquirir um sinal eléctrico cuja tensão corresponde a
um dado caudal. A turbina é ligada a uma fonte de alimentação de 24 Volt e o sinal de saída
em amperes, é convertido em Volts através de uma resistência pré-definida, tendo em atenção
a voltagem máxima da placa de aquisição que é de 10 Volt.
A curva de calibração é apresentada no Apêndice II – Figura A.II.16.
25
2.Projecto da instalação experimental
Após o arranque da instalação verificou-se que os caudais medidos eram bastante
elevados, e que o sinal obtido pelo debitómetro de turbina tinha sempre muito ruído
conduzindo a grandes flutuações na determinação do caudal de água. Assim optou-se por
utilizar um rotâmetro, que embora não permita uma ligação ao sistema de aquisição de dados,
permitiu uma certeza muito maior na determinação do caudal de água. A curva de calibração
do rotâmetro está também apresentada no Apêndice II – Figura A.II.17.
Depois das dimensões da instalação estarem estabelecidas passou-se a definir a posição
mais adequada para a instalação dos termopares e dos transdutores de pressão, que permitiram
a leitura contínua da temperatura dos gases, da água e da pressão ao longo de todos os
ensaios.
2.6 Localização dos termopares tipo K
Todos os termopares estavam ligados a uma placa de aquisição de dados UPC601-T com
14 bit de resolução e 14 entradas. Os que foram usados para medir a temperatura do lado dos
gases eram todos com bainha e com as seguintes dimensões: dtp=1 mm, ltpb=150 mm. Os
usados para o lado da água correspondiam apenas a fio de termopar previamente soldado.
A definição das várias posições ocupadas por cada termopar na coluna foi a seguinte:
- Colocou-se um termopar no interior do leito junto ao distribuidor - TL;
- Colocaram-se três termopares em cada secção radial junto às flanges. Como existiam
três flanges usaram-se 9 termopares;
- Usou-se fio de termopar para medir a temperatura na entrada e na saída de cada
permutador do lado da camisa por onde circula a água. Como existiam dois
permutadores, usaram-se quatro termopares nesta zona.
Estas várias posições dos termopares vêm referidas na Figura 3.2 do Capítulo 3, onde se
representa o esquema da instalação.
26
2.Projecto da instalação experimental
2.7 Localização das tomas de pressão
Todas as medidas de queda de pressão foram obtidas por transdutores de pressão da
marca Omega série PX140, que se encontravam ligados a uma placa de aquisição de dados
PCI–DAS 1606/16 de 16 bit e 16 entradas
Colocou-se um tubo de aço junto ao distribuidor, que foi ligado a um dos transdutores
que permitia saber continuamente a queda de pressão no leito. O transdutor usado para medir
a pressão no leito é da série PX142-002D5V. A respectiva curva de calibração está
apresentada no Apêndice II – Figura A.II.4
Em cada secção radial e também junto às flanges foram colocadas três tomas de pressão
que se ligam num anel entre si que por sua vez é ligado a um transdutor de pressão
2.8 Válvula derivadora
Esta válvula derivadora do caudal de sólidos foi instalada a seguir ao ciclone e só tem
duas posições:
- uma delas permite que todos os sólidos sigam o trajecto directo até à válvula borboleta
e possam ser admitidos na coluna;
- a outra posição permite recolher os sólidos separados pelo ciclone, havendo assim
possibilidade de determinar o caudal mássico de sólidos transportado pela corrente gasosa.
2.9 Válvula borboleta
Esta válvula foi escolhida para ser uma peça fundamental na circulação de sólidos na
coluna pois garantia a ligação entre o leito e o braço descendente. A maior ou menor abertura
desta válvula é conseguida através de uma roda dentada. Desta forma, permitia equilibrar a
pressão na coluna e garantir assim a alimentação dos sólidos que eram arrastados pela
corrente gasosa e que, ao passar pelo ciclone pela acção da força centrífuga iam cair ao longo
do braço descendente.
27
2.Projecto da instalação experimental
Apresenta-se de seguida na Figura 2.2 uma fotografia da instalação experimental e na
Figura 2.3 uma imagem da instalação com a respectiva legenda. Um esquema representativo
da zona de trabalho com as respectivas dimensões é apresentado na Figura 2.4.
Figura 2.2 Fotografia da instalação experimental
28
2.Projecto da instalação experimental
Ciclone
Termopares
Válvula derivadora
Entrada
de areia
2º Permutador
de parede de
membrana
Medidor de
caudal de
água
1º Permutador
de parede de
membrana
Medidor de
caudal de
propano
Medidor de
caudal de ar
Toma de
pressão
Entrada
de ar
Entrada de
propano
Retorno
de areia
Válvula de
borboleta
Figura 2.3 Fotografia da instalação experimental com a respectiva legenda
29
2.Projecto da instalação experimental
Figura 2.4 Desenho da instalação referente à zona de trabalho e dimensões mais importantes.
30
3. Procedimento experimental
3.Procedimento experimental
Neste capítulo é apresentado, juntamente com o esquema da instalação experimental,
todo o procedimento usado nos ensaios que foram feitos sem combustão e também nos que
foram realizados posteriormente com a admissão de propano à coluna.
Para que se desse início à parte experimental foi necessário previamente caracterizar os
vários tipos de areia que iriam constituir o leito de partículas.
3.1 Preparação da areia a usar como enchimento do leito – sua caracterização
Fez-se uma peneiração prévia da areia num vibrador de marca Retsch modelo AS200Basic. Primeiro, usou-se a seguinte série de peneiros de Taylor (malha em µm):
90<125<160<200<250. Juntou-se então a areia que ficou no peneiro de 90 µm, a que ficou no
de 125 µm e por fim a retida no peneiro de 160 µm, e, obtiveram-se três granulometrias
distintas com os seguintes diâmetros médios: dp=107,5 µm, dp=142,5 µm, e dp=180 µm.
Como se dispunha de outro saco de areia mais grossa da mesma origem passou-se a uma
outra peneiração no mesmo vibrador mas usando uma série de peneiros diferentes (malha em
µm): 200<250<315<400. Nesta fase obtiveram-se mais duas granulometrias distintas:
dp=282,5 µm, areia retida no peneiro de 250 µm, e dp=357,5 µm, areia retida no peneiro de
315 µm.
Tendo em atenção os cinco tamanhos diferentes de partículas, foi necessário caracterizar
cada tamanho de areia no que diz respeito aos seguintes parâmetros: massa volúmica das
partículas, ρp, massa volúmica do leito, ρL, e porosidade mínima de fluidização, εmf .
31
3. Procedimento experimental
3.1.1 Caracterização da massa volúmica de cada tamanho de partículas, ρP – Método do
picnómetro
Este método experimental consiste no seguinte,
a) pesar o picnómetro vazio = a
b) pesar o picnómetro com água destilada = b
c) pesar o picnómetro com areia até cerca de 1/3 da sua capacidade = c
d) perfazer com água o ponto c) e pesar o conjunto = d
20
d 20
=
c−a
(b − a ) − ( d − c )
(3.1)
Para determinar a densidade da areia referida à água a 4 ºC (referência usual para
líquidos e sólidos), basta multiplicar o resultado obtido na expressão anterior pela densidade
da água a 4 ºC, ou seja
d
20
4
= d agua ,4 × d 2020
ρ p = d 420 ×1000 (kg/m3)
(3.2)
(3.3)
3.1.2 Determinação da massa volúmica do leito -ρL
Este parâmetro é importante para que se possa ter uma primeira estimativa da
quantidade de areia a pesar de modo a garantir uma pressão inicial no leito de 100 a 150 mm.
Este valor é indicado pela sonda de pressão previamente introduzida no leito e ligada a um
dos transdutores de pressão já referidos.
Para cada uma das granulometrias pesa-se uma dada quantidade de areia, cerca de 400 a
500 g e mede-se o respectivo volume numa proveta de 500ml.
ρL =
32
massa
volume
(3.4)
3. Procedimento experimental
3.1.3 Porosidade mínima de fluidização
Esta determinação foi feita por dois métodos:
1º método
a) Pesou-se uma dada quantidade de areia (cerca de 40 a 50 g)- mareia - na balança
decimal e mediu-se o volume correspondente numa proveta de 50 mL- Vt.
b) Juntou-se à areia 50 mL de água medidos em pipeta de 50 mL, e anotou se o volume
de água sobrenadante. A diferença entre estes dois valores correspondeu ao volume de
vazios.
c) O valor da porosidade corresponde a
ε mf =
Vvazios
Vtotal
(3.5)
2º método
Determina-se o volume ocupado pelas partículas de areia através da quantidade da
mesma que foi pesada na alínea a) do método anterior, e da determinação já feita da massa
volúmica das partículas. Deste modo tem-se
Vareia =
ρp
mareia
(3.6)
Tendo em atenção o volume referido na alínea a) do 1º método, pode-se calcular a porosidade
mínima de fluidização
ε mf =
Vt − Vareia
Vt
(3.7)
Os ensaios foram repetidos várias vezes até obter resultados concordantes. Os valores
obtidos para cada um destes parâmetros referentes a cada granulometria vêm apresentados no
Apêndice I.
Dada a pequena dimensão das partículas, este segundo método foi o que permitiu obter
resultados mais concordantes.
33
3. Procedimento experimental
3.2 Ensaios de transferência de calor na coluna
O arranque experimental numa coluna destas dimensões foi muito importante para
permitir um primeiro teste às condições óptimas de operação e à flexibilidade do sistema no
que diz respeito aos caudais de gás a usar. Permitiu também uma análise primária dos
fenómenos de transferência de calor que parecem ocorrer do leito para a parede do
permutador e no próprio permutador, nomeadamente:
- Condução axial;
- Radiação directa do leito para a parede interna do permutador;
- Radiação com meio participante no caso de existir reacção de combustão;
- Convecção da mistura gasosa para a parede interna do permutador;
- Convecção e condução devido ao movimento das partículas.
E para que se possam estudar estes fenómenos, tentando eliminar de alguma forma as
incertezas inerentes às limitações da instalação experimental, que podem de algum modo
induzir em erros de interpretação destes mesmos fenómenos, é de primordial importância
definir muito bem o ciclo experimental. Só assim o tratamento de dados a fazer
posteriormente poderá ser de algum modo conclusivo.
Deste modo, as várias fases definidas neste procedimento experimental dos ensaios sem
combustão e com combustão, visaram a possibilidade de estudar posteriormente todos os
efeitos que podiam estar em jogo num trabalho deste tipo. As várias fases experimentais para
cada ensaio constaram do seguinte:
- Escoamento do ar com aquecimento eléctrico e estabelecimento de um estado
estacionário para as condições de arranque;
- Altura adequada para fazer a alimentação do propano e iniciar o processo de
combustão;
- Deixar decorrer o processo de queima tanto tempo quanto possível, de modo
garantir a ocorrência de um estado estacionário;
- Analisar a variação da pressão no leito e na zona de transporte durante todo o
ensaio;
- Cortar a alimentação de propano quando se notava o fim da queima, mas continuar
com o escoamento de ar de maneira a que se atinja novo estado estacionário;
- Cortar a entrada de ar, mas manter durante algum tempo a resistência eléctrica;
- Desligar a resistência eléctrica;
- Fechar a corrida depois de atingido um estado pseudo – estacionário.
34
3. Procedimento experimental
Uma vez que neste trabalho se pretendeu um estudo exaustivo da transferência de calor
em leitos fluidizados fez todo o sentido o estudo dos mecanismos envolvidos na transferência
de calor numa fase em que não se introduzia o propano, e portanto não se provocava a reacção
de combustão. Além desta fase ser importante, deve contribuir para um melhor entendimento
dos mecanismos adicionais de transferência de calor que estão presentes aquando da reacção
de combustão.
3.3 Ensaios sem combustão
A execução experimental teve sempre como primeira fase a ligação do computador e a
abertura do programa previamente criado e testado para aquisição de dados, que neste caso foi
o programa “LabTech Notebook”. Além disso, para que os dados adquiridos correspondessem
efectivamente às condições de calibração dos vários aparelhos, foi preciso acertar sempre a
fonte de alimentação para o valor de 7,99 – 8,00 Volt.
Antes de passar à descrição do procedimento experimental, mostra-se na Figura 3.1 uma
visualização do monitor do PC, durante o decorrer de um dos muitos ensaios efectuados.
Figura 3.1-Visualização do ecrã do PC durante um dos ensaios sem combustão, TL=600 ºC.
35
3. Procedimento experimental
Nesta imagem apresentada na Figura 3.1, o valor da potência, do caudal de propano e da
razão A/C não correspondem a valores reais já que este ensaio foi realizado sem combustão.
Deste modo os valores apresentados nestas células deveriam ser zero, mas o programa estava
preparado para apresentar valores destas variáveis na situação de combustão. Por outro lado o
termopar designado por Tag 4E apresenta um valor negativo porque estava desligado da placa
de aquisição.
O arranque da parte experimental foi feito com as partículas de diâmetro médio de
180 µm e o procedimento constou no seguinte:
1. Foi introduzida uma dada quantidade de areia na coluna através do braço descendente.
A quantidade de areia que é deixada cair para o distribuidor é controlada pela
manipulação da válvula borboleta. Essa válvula é fechada quando a pressão no leito
atingir o valor desejado - cerca de 10 a 15 cm de água.
2. Abriu-se a válvula de entrada do ar, verificando se a pressão relativa no manómetro
marcava 400 mbar, e, regulou-se o caudal pretendido com o auxílio da válvula agulha
acoplada à respectiva placa de orifício. As condições de arranque corresponderam a
um caudal de ar de 1 kg/h.
3. Ligou-se a resistência eléctrica fixando no “set-point “ a temperatura desejada.
4. Abriu-se a água controlando o caudal com o uso da válvula agulha para um valor
previamente definido. O redutor de pressão, colocado na admissão da água da rede,
deve ser regulado para 1,5 kgf/cm2.
5. Quando a temperatura no leito atingia o valor previamente fixado mantinha-se o
ensaio a decorrer durante algum tempo, cerca de 1000 s e, nessa altura, a alimentação
de ar era cortada, mantendo a resistência ligada.
6. Desligou-se a resistência eléctrica
7. Fechava-se a corrida quando se verificava que não havia variação da temperatura da
água na saída.
36
3. Procedimento experimental
Nestes ensaios sem combustão pretendeu-se para cada granulometria estudar a
influência das seguintes variáveis:
- Caudal de água;
- Temperatura do leito;
- Caudal de ar.
O esquema da instalação experimental vem apresentado na Figura 3.2
Ciclon
e
Gases
Tramo 2
Fio de
termopares
Tage
Tge
Tramo 1
Tgs
Tags
Saída de
Água
Tomas de
pressão
Válvula
Descarga
da areia
Sonda de
pressão
Termopar
Leito
Termopares
com bainha
Entrada
da areia
Entrada
de Água
Distribuidor
Placa
orifício
Ar comprimido
Propano
400 mbar
400 mbar
Figura 3.2 – Esquema da instalação experimental
37
3. Procedimento experimental
3.3.1 Análise da influência do caudal de água: 35 kg/h <mag < 140 kg/h
- Fixou-se o valor da temperatura do leito;
- Verificou-se o valor da pressão no leito para que se mantivesse entre 10 e 15 cm de água.
(podia ser necessário retirar areia do leito ou repô-la);
- Ligou-se a resistência eléctrica;
- Fixou-se o caudal de ar em 1 kg/h;
- Abriu-se a válvula do rotâmetro para fixar o flutuador numa dada posição - os ensaios são
feitos para pf = 16; pf = 35; pf = 69;
- Deixou-se atingir as condições de estado estacionário;
- Manteve-se o ensaio durante cerca de 1000 s e nessa altura cortou-se a alimentação de ar
mantendo a resistência ligada;
- Desligou-se a resistência eléctrica;
- Fechou-se a corrida quando se verificou que não havia variação da temperatura da água na
saída
Repete-se este procedimento até obter resultados concordantes e só depois disso é que se
faz outro ensaio para um outro caudal de água, mantendo a temperatura do leito, a pressão e o
caudal de ar constante.
3.3.2 Análise da influência da Temperatura do Leito: 400ºC <TL< 700ºC
Estes ensaios foram feitos para o caudal de água de 73 kg/h, para um caudal de ar de
1 kg/h e para uma pressão no leito de 14 cm.
O procedimento foi em tudo análogo ao referido no ponto 3.3.1.
Para algumas partículas também se fez esta análise para o caudal de água de 35 kg/h e
para 140 kg/h.
3.3.3 Análise da influência do caudal de ar: 0,82 kg/h <mar< 1,5 kg/h
Fixou-se a temperatura do leito num dos valores da gama referida em 3.3.2, fixou-se o
caudal de água em 73 kg/h, a pressão do leito em 14 cm e para um dos caudais de ar repetiuse todo o procedimento referido em 3.3.1, tendo sempre o cuidado de deixar atingir estado
38
3. Procedimento experimental
estacionário. Depois de finalizar um ensaio, e mantendo todos os parâmetros fixos, mudou-se
apenas o caudal de ar. Repetiu-se novamente o procedimento anterior.
Só depois de se terem obtido resultados concordantes em todos os itens referidos é que
se deve fazer a descarga da coluna e inserir nova granulometria de areia.
3.4 Ensaios com combustão
Nos ensaios com combustão, o procedimento experimental foi o mesmo do referido no
ponto 3.3. até ao item designado pelo nº 4. Assim, e depois de se atingir um estado
estacionário de acordo com a temperatura fixada para o leito que, neste caso, deve ser de
720ºC, o procedimento passou a ser o seguinte:
1. Introduziu-se o propano abrindo a válvula de admissão respectiva. Fixou-se a pressão do
manómetro em 400 mbar. O caudal de propano nas condições de arranque deve situar-se
entre 0,11 e 0,12 kg/h de maneira que a relação A/C (quociente entre o caudal mássico
de ar e de propano) se mantenha entre 8 e 10; ou seja o valor da riqueza da mistura r,
deveria ser maior do que 1. Isto significa que se trabalhou sempre em condições de
mistura rica (defeito de ar)
2. Deve-se deixar o ensaio decorrer tanto tempo quanto o possível tendo em atenção o
ruído característico da combustão, a saltação das partículas e a variação da temperatura
do leito; foi a indicação deste valor um dos parâmetros fundamentais da progressão e
manutenção da reacção de combustão.
3. Quando se deixou de ouvir ruído, ou se começou a sentir um cheiro característico do
propano não queimado, e simultaneamente a temperatura do leito começava a descer,
era necessário ter logo o cuidado de fechar a válvula de corte que interrompia a entrada
de propano na coluna.
4. Mantinha-se o escoamento do ar e a resistência ligada deixando-se o ensaio atingir
condições próximas das condições de arranque antes da alimentação do propano.
5. Quando a temperatura de saída da água se mantinha constante devia-se então cortar o ar
mantendo ainda a resistência ligada. Deixava-se ainda durante algum tempo o ensaio a
decorrer nestas condições.
39
3. Procedimento experimental
6. Desligava-se a resistência eléctrica e deixava-se o ensaio a decorrer até que a
temperatura da água na saída se mantivesse constante.
7. O ensaio dava-se por terminado, e restava então tratar os dados no que diz respeito às
temperaturas, pressões, potências e caudais registados no programa de aquisição.
Para começar novo ensaio era necessário verificar a quantidade de areia no leito. Isto era
feito através da análise do valor da pressão do leito com o ar a circular nas condições de
fluidização mínima e à temperatura ambiente. Foi em geral preciso repor areia na coluna por
manipulação da válvula borboleta. A altura do leito é um parâmetro fundamental para
conseguir atingir a temperatura necessária à queima de propano. Se esse valor ultrapassava os
20 cm tornava-se difícil atingir no leito temperaturas superiores a 700 ºC, com a potência de
aquecimento disponível de 2 kW.
Deve-se procurar repetir os ensaios as vezes necessárias, mantendo as variáveis como:
pressão no leito, temperatura de arranque, caudal de água, caudal de ar e caudal de propano, o
mais possível constantes, para poder testar a reprodutibilidade dos mesmos. É de esperar que
haja alteração dos resultados obtidos pois as próprias condições atmosféricas de pressão,
temperatura e humidade relativa do ar vão ter influencia na progressão da reacção de
combustão.
Nesta segunda fase os ensaios foram então feitos nas seguintes condições:
- Temperatura do leito;
700 ºC < TL < 730 ºC
- Pressão do leito;
8 cm < PL< 15 cm
- Caudal de água de arrefecimento;
35 kg/h < mag < 140 kg/h
Nota: Quanto ao caudal de água, numa primeira fase em que estava instalado o
debitómetro de turbina, os caudais obtidos eram muito elevados e sempre superiores a
120 kg/h; além de que o sinal de tensão obtido sofria grandes oscilações devido ao ruído. Para
poder trabalhar com caudais mais baixos foi então necessário instalar um rotâmetro cuja curva
40
3. Procedimento experimental
de calibração se apresenta no Apêndice II- Figura A.II.17 - e como se pode constatar permitia
trabalhar numa gama de caudais de 30 a 200 kg/h.
- Caudal de ar e propano
0,85 kg/h <mar < 1,2 kg/h
0,1 kg/h < mpro < 0,12 kg/h
Através dos vários ensaios efectuados verificou-se existir pouca flexibilidade no que diz
respeito ao caudal de ar e consequentemente ao caudal de propano a admitir à coluna nas
condições de arranque da combustão.
Por um lado, a potência de aquecimento disponível é pequena, 2000 W, o que
condicionou o caudal de fluidização e o tempo de aquecimento do leito. Por outro lado, a
velocidade de propagação de uma chama numa pré-mistura reagente varia dentro de limites
muito apertados. Por isso, para se garantir a permanência da chama logo acima do leito ou
mesmo no interior deste, quando a sua temperatura é elevada, a gama de operação do caudal
de ar é igualmente apertada.
Como se pretendia medir a transferência de calor numa situação o mais próxima
possível da situação real, em que há voláteis que são libertados pelas partículas sólidas e que
depois queimam na fase gasosa em condições de defeito de ar, houve que por um lado
escolher premeditadamente um abastecimento do reactor com misturas propano/ar ricas, e,
por outro lado trabalhar num espectro muito reduzido de caudais.
Pretendia-se com este trabalho que o caudal de ar fosse suficientemente alto para
garantir condições de transporte de sólidos, mas também era estritamente necessário que a
temperatura no leito fosse superior à temperatura de auto-ignição do propano para poder
garantir a sua queima. Ora, uma vez que o ar é admitido do exterior, e que os ensaios se
iniciaram no Inverno, verificou-se que só para caudais baixos – cerca de 1 kg/h- é que se
conseguiam atingir as condições óptimas de arranque, uma vez que a resistência eléctrica
instalada tinha uma potência de 2000 W. Isto teve como consequência, e como aliás já foi
referido a limitação dos caudais de propano a alimentar à coluna.
Procurou-se estudar os efeitos da granulometria, e de alguma variação, embora muito
pequena, dos caudais de gás na reacção de combustão de propano e consequentemente na
transferência de calor para água.
41
3. Procedimento experimental
Todos estes ensaios com combustão são repetidos para os cinco tamanhos diferentes de
partículas, para que se possa analisar a influência da granulometria na reacção de combustão.
Para fazer a descarga da coluna é preciso que toda a areia seja encaminhada para o braço
descendente para depois ser retirada. Para isso é preciso retirar a mangueira de alimentação de
propano e colocar aí uma outra mangueira, ligada à instalação de ar comprimido, que permita
estabelecer um caudal de ar capaz de arrastar a areia para fora do reactor.
A indicação de que a coluna está vazia é dada pelo valor da pressão do leito. Quando o
valor registado for zero é sinal que a zona do leito se encontra vazia.
Procede-se então a nova recarga na coluna com areia de outra granulometria. A nova
granulometria é introduzida pelo braço descendente, tendo o cuidado de verificar se
inicialmente a válvula borboleta se encontra fechada. Só depois, e com ar a circular, é que se
vai abrindo a referida válvula para que a areia vá caindo devagar para a placa acima do
distribuidor. Quando a pressão do leito atingir o valor desejado fecha-se a válvula, e a coluna
está então, em condições para novo arranque.
Como a areia tinha tendência a deslocar-se através dos furos do distribuidor caindo para
o plenum, era necessário manter sempre a escoar um caudal mínimo de ar que limitava tal
passagem da areia pelo distribuidor.
42
4. Análise prévia dos resultados experimentais
4.Análise prévia dos resultados experimentais
4.1 Regime de escoamento no leito nas condições de operação
Embora houvesse intenção inicial de se trabalhar em regime de fluidização turbulenta e
até mesmo em regime circulante, a quantidade de informação recolhida nestas duas situações
e leito quase estacionário foi muito elevada. Optou-se por isso, no presente trabalho, por
considerar apenas como condições operacionais o leito a funcionar em regime borbulhante,
quase-estacionário sem e com combustão, já que esse tipo de escoamento se encontra pouco
desenvolvido na literatura Científica.
Este critério de leito quase-estacionário deve-se ao facto de que, em condições de
funcionamento com combustão, o carácter explosivo desta no instante em que as bolhas da
mistura reagente afloram à superfície do leito, levavam a uma projecção de partículas para
fora do leito. Nesta situação de combustão, o leito ia perdendo matéria ao longo do tempo,
conforme se pode verificar pela evolução da queda de pressão no leito ao longo dos ensaios.
Em funcionamento sem combustão, embora as partículas fossem projectadas para fora
do leito, voltavam de novo ao leito por acção da gravidade.
Se se atender às condições operatórias relativamente à velocidade superficial do ar e à
velocidade terminal das partículas para a gama de temperaturas de trabalho, 400 ºC < TL < 700ºC,
e para os caudais de ar usados, 0,85 kg/h < mar < 1,5 kg/h, tem-se o seguinte:
- Velocidade superficial do ar à temperatura do leito: 0,2 m/s < v0 < 0,5 m/s;
- Velocidade terminal para cada granulometria : pode ser analisada na Tabela 4.1
43
4. Análise prévia dos resultados experimentais
Tabela 4.1 Valores das velocidades terminais em função do diâmetro médio das partículas, para as
temperaturas do leito usadas
dp(µm)
vt(m/s)
107,5
0,41 a 0,35
142,5
0,71 a 0,60
180
1,0 a 0,90
282,5
2,1 a 1,9
357,5
2,9 a 2,7
Pela análise destes valores verifica-se que a velocidade terminal das várias partículas
está sempre acima da velocidade superficial do ar. Só no caso das partículas mais pequenas e
em situações de caudais mais altos e temperaturas mais altas é que, eventualmente, se poderão
atingir velocidades terminais mais baixas do que a velocidade superficial do gás.
Assim, na zona do permutador, apesar de não haver um fluxo constante de partículas, o
excesso de gás que sobe sob a forma de bolhas vai provocar um movimento migratório de
partículas que são arrastadas com as bolhas de gás. Estas rebentam à superfície, provocando
um espalhamento de partículas que atingem a zona do permutador. Algumas, as mais finas,
poderão ser arrastadas pelo gás, mas a maior parte voltará de novo ao leito. Este movimento
será tanto mais acentuado quanto menor for a dimensão das partículas.
Pela análise da pressão do leito e da pressão na zona de transporte, durante os vários
ensaios da primeira fase- ensaios sem combustão - verifica-se que ambas as pressões se
mantêm constantes, o que é uma prova de que as partículas embora se afastem do leito voltam
para lá de novo. Este movimento das partículas tipo “espalhamento” vai, no entanto,
influenciar muito a transferência de calor na zona do permutador.
Apenas se conseguiu transporte de partículas acima de TDH nos ensaios em que houve
a queima de propano. Nestes ensaios da segunda fase é evidente a variação de pressão que
ocorre no leito, durante o tempo em que decorre a reacção de combustão. No entanto, esta
variação só é constatada para as três granulometrias mais baixas. Sendo os caudais de ar da
mesma ordem de grandeza dos usados nos ensaios sem combustão, este transporte de sólidos
foi devido às explosões provenientes da queima do propano, e, novamente, vai ser estudada a
influência deste transporte de partículas na taxa de transferência de calor.
É portanto necessário fazer uma caracterização prévia do regime de escoamento no leito
de partículas, para que se possa relacionar posteriormente esse tipo de regime com a taxa de
transferência de calor para a água, nos ensaios com e sem combustão. Esta análise é feita
detalhadamente no Capítulo 5.
44
4. Análise prévia dos resultados experimentais
4.2 Análise do calor trocado no primeiro permutador, sem combustão do propano
Uma das primeiras constatações, depois de trabalhar os dados obtidos no programa de
aquisição, foi a diferença existente entre o calor recebido pela água de arrefecimento e o que
correspondia à variação de entalpia do ar, ainda sem reacção de combustão do propano.
O cálculo da variação da entalpia do ar já foi feito tendo em consideração a diferença
existente entre as leituras registadas pelos termopares e os valores reais da temperatura do
lado do ar. Como se explica no ponto 4.2.2, sempre que as sondas de temperatura estão
inseridas em condutas de pequena dimensão, em que a temperatura dos gases é muito
diferente da temperatura da parede, o efeito da radiação tem de ser considerado.
Desta forma, pode-se dizer que a energia recebida pela água, não foi só a cedida pelo ar
por convecção ao longo do permutador, mas foi também, o resultado da contribuição de
outros mecanismos, nomeadamente:
- energia de radiação directamente do leito para a parede do permutador;
- energia associada ao movimento das partículas quentes que se soltam do leito e
retornam ao mesmo, quando o leito se encontra em escoamento borbulhante.
Assim sendo, e constatando que qag > qar, um balanço de energia à coluna incluindo
zona do leito e permutador de calor conduzirá:
qag = qar + qradL + qp
(4.1)
Esta análise foi feita no permutador 1, assim como no permutador 2. No entanto, neste
último, a quantidade de calor transferida é tão pequena, que só vai ser importante a
transferência de calor que ocorreu no primeiro permutador.
Como o que se pretende é conhecer o peso de cada uma das parcelas do segundo
membro da equação 4.1, começou por se calcular o valor do calor recebido pela água, tendo
em atenção a variação da sua entalpia,
qag = m ag c p (Tags − Tage )
sendo o resultado desta equação que vai
(4.2)
permitir determinar o coeficiente global de
transferência de calor. É também feita a análise de incertezas no Apêndice III, destes valores
experimentais obtidos.
45
4. Análise prévia dos resultados experimentais
Fez-se em seguida uma análise dos fenómenos de transferência de calor que ocorreram
no permutador, para os ensaios com as partículas de dp=180 µm e não considerando ainda a
reacção de combustão. Se for analisado o resultado obtido nalguns dos ensaios sem
combustão e já para uma temperatura do leito próxima da temperatura de admissão do
propano, nomeadamente:
- TL = 700 ºC;
- mar = 1kg/h;
- mag = constante.
verifica-se novamente, que o calor cedido pelo ar é inferior ao recebido pela água. Isto pode
ser constatado nos gráficos que se seguem, para três caudais de água diferentes:
Potência témica (W) e T L(ºC)
800
700
600
500
400
300
200
100
0
0
200
400
600
800
1000
tempo(s)
TL
água
ar
Figura 4.1 Variação da entalpia do ar e da água para as condições de operação,TL=700 ºC; PL=10cm;
mar= 1 kg/h; dp=180 µm, mag = 35kg/h.
46
4. Análise prévia dos resultados experimentais
Potência térmica (W) e T L(ºC)
800
700
600
500
400
300
200
100
0
0
200
400
600
800
1000
tempo(s)
TL
água
ar
Figura 4.2 Variação da entalpia do ar e da água para as condições de operação,TL=700 ºC; PL=10 cm;
mar=1 kg/h; dp=180 µm, mag =73 kg/h.
Potência térmica (W) e TL(ºC)
800
700
600
500
400
300
200
100
0
0
200
400
600
800
1000
tempo(s)
TL
água
ar
Figura 4.3 Variação da entalpia do ar e da água para as condições de operação, TL=700 ºC; PL =10 cm;
mar =1 kg/h; dp =180 µm, mag =140 kg/h.
Com base nos resultados obtidos, pode-se constatar o seguinte:
1. a potência térmica transferida para a água de arrefecimento é independente do caudal de
água que atravessa a camisa. Então a resistência térmica dominante deverá estar
localizada do lado interno do permutador;
47
4. Análise prévia dos resultados experimentais
2. a transferência de calor para a água, além de radial, também poderá ter uma componente
de condução axial;
3. uma das contribuições a ter em consideração para o aquecimento da água, não será
apenas a variação de entalpia do ar, mas também, o calor transferido por radiação
directamente de um leito fluidizado borbulhante para a parede do permutador, e ainda, o
calor transferido devido ao movimento migratório das partículas que são projectadas
para fora do leito, evoluem até chocar com as paredes confinadoras, e voltam a cair
dentro do leito.
Uma vez que os resultados experimentais, como os mostrados nas Figuras 4.1. ,4.2 e 4.3
parecem ser independentes do caudal de água que circula na camisa, o valor do coeficiente de
convecção do lado da água pode ser determinado. Para isso recorre-se a equações clássicas
apresentadas na literatura Científica para escoamento de um fluido através de um espaço
anelar, e para a gama de valores de Reynolds adequada às condições operatórias.
Relativamente à componente axial referida no ponto 2 acima, a maneira mais adequada
que se encontrou para a poder determinar experimentalmente está expressa no procedimento
experimental, e mais uma vez se expõe:
- quando em cada ensaio se atingem as condições de estado estacionário fecha-se o ar
mantendo a resistência eléctrica ligada. Como a temperatura do leito sobe bruscamente, a
resistência eléctrica apesar de não ter sido desligada deixa de estar activa pelo que se pode
desligar praticamente logo. O que se verifica como se pode constatar na Figura 4.4 é que a
variação da entalpia da água desce também bruscamente, apesar do leito estar agora mais
quente. Com este procedimento pode-se analisar a componente de condução axial -é o
objectivo- mas também a componente relativa à radiação. Quanto à radiação, que à partida
seria uma componente mais importante nesta fase, dada a maior temperatura do leito, parece
agora não ter significado. Para isso terá contribuído o facto do leito ter passado de fluidizado
borbulhante, a leito fixo. Por outro lado, o facto de se cortar o escoamento do ar, faz com que
a transferência de calor por convecção forçada deixe de existir e então a transferência de calor
para a água ocorre apenas por condução ao longo da parede. É essa a componente axial que
tem de ser analisada para que se possa decidir se será ou não importante incluí-la nos cálculos
posteriores.
Este resultado pode ser constatado na Figura 4.4, que é um ensaio típico de todos os que
foram realizados:
48
4. Análise prévia dos resultados experimentais
Potência térmica (W) e TL(ºC)
900
800
700
600
500
400
300
200
100
0
0
300
600
900
1200
1500
tempo(s)
TL
água
ar
Figura 4.4 Variação da entalpia do ar e da água para as condições de operação, TL= 700 ºC; PL = 13 cm;
mar =1 kg/h; dp =180 µm; mag =73 kg/h, com corte de ar.
Todos os ensaios foram feitos, da mesma maneira, visando a determinação desta
componente de calor por condução axial, para se ter sempre a certeza do seu peso no computo
geral.
Relativamente ao ponto 3, desta secção 4.2, para poder determinar a transferência de
calor por radiação do leito enquanto fluidizado para a parede interna do permutador foi
necessário arranjar um modelo que permitisse quantificar essa mesma quantidade de calor.
Vários modelos são apresentados em bibliografia, mas todos eles tratam o fluxo de partículas
que sobe ao longo da zona de transporte, e as paredes do permutador, como placas paralelas.
Este, não será certamente o modelo adequado a este trabalho, dadas as condições de operação
e o facto do principal movimento das partículas ser um movimento de vai e vem.
No caso presente tínhamos duas situações distintas relativamente ao movimento das
partículas. No caso de funcionamento sem combustão havia um movimento de vai e vem das
partículas, e no caso do funcionamento com combustão, adicionado a este, havia também
transporte de sólidos mais finos ao longo do permutador. Este transporte adicional de
partículas pode tornar mais complexa a análise do calor transferido por radiação.
Optou-se por se considerar a transferência de calor das partículas quer por radiação, quer
por condução/convecção, como um todo indissociável designando esse termo por calor
transferido pelas partículas, qpexp. O restante calor transferido por radiação foi essencialmente
o trocado entre o leito e as paredes internas do permutador. Para isso, considerou-se o leito
formado pelas paredes acima da superfície do mesmo, e, por um disco circular com área igual
49
4. Análise prévia dos resultados experimentais
à secção recta do reactor, que corresponde à própria superfície do leito. Este modelo vem
apresentado na secção 4.3 deste Capítulo 4.
Como conclusão, toda esta análise pressupõe antes de tudo o conhecimento do
coeficiente de convecção do lado da água, he, e assim a determinação do valor da temperatura
da parede exterior do tubo interno. Só depois, pela análise da resistência de condução da
parede interna, é que se determina a temperatura interna dessa mesma parede. Esse valor, da
temperatura da parede vai permitir também, fazer as correcções das temperaturas lidas pelos
termopares, devido ao efeito de radiação para a parede.
4.2.1 Estimativa da temperatura da parede interior do tubo interno do permutador
O calor transferido da parede exterior do tubo interno do permutador para a água ocorre
por convecção forçada. É portanto necessário, para cada caudal imposto, saber o tipo de
regime de escoamento do lado da água e assim recorrendo a correlações empíricas, determinar
o valor médio do coeficiente de convecção do lado exterior, he.
Para os vários caudais de água tratados e que podem variar entre 35 a 140 kg/h - ver
Figura A.II.17, são calculados os limites de Reynolds - Re.
Se for definido deq como sendo 4*Aesc/Pm , então
Re= 4mag/(Pm.µag)
(4.3)
A gama de trabalho para este valor de Reynolds situou-se,
95< Re <433
Conclui-se que seja qual for o caudal de água, o regime de escoamento será sempre laminar.
Para poder usar a relação empírica apresentada em Ozisik (1985) e proposta por Sieder e
Tate é preciso garantir que a zona de transferência de calor seja uma zona
hidrodinamicamente e termicamente desenvolvida. No caso de isso não acontecer, ter-se-à
50
4. Análise prévia dos resultados experimentais
valores do número de Nusselt maiores, a que correspondem valores maiores de he e portanto
resistência térmica menor.
Os valores dos comprimentos de entrada hidrodinâmico, Lh, e térmico, Lt, são
calculados pelas relações, segundo Ozisik (1985)
(Lh/deq)/Re = 0,056
(Lt/deq)/(Re.Pr) = 0,033 (para Tw constante)
e os resultados obtidos para a gama de Reynolds referida são:
0,05 m< Lh <0,24 m
0,21 m< Lt <0,95 m
Tendo cada permutador uma altura de cerca de 1m, e de acordo com estes valores de Lh
e Lt, é natural que a zona de transferência de calor se encontre hidrodinâmicamente
desenvolvida e termicamente em desenvolvimento para os caudais mais baixos de água. Para
os caudais mais altos, pode acontecer estar-se numa zona em desenvolvimento quer térmico
quer hidrodinâmico. Deste modo, a correlação proposta por Sieder e Tate pode conduzir a
algum erro. No entanto, como foi provado pelos gráficos apresentados no ponto 4.2, a
resistência dominante não está do lado da água e portanto apenas interessa uma estimativa do
coeficiente de convecção desse lado. Pode-se então aplicar a correlação proposta por Sieder e
Tate, apresentada por Ozisik (1985),
Nue = 1,86(Re Pr
d eq
L
1/ 3
)
 µag 


 µw 
0 ,14
(4.4)
válida para regime laminar; Re<2100 e RePrdeq/L >100
Esta última restrição não é obedecida, mas pode ser usada a mesma equação admitindo um
erro de 20%.
Desprezando o termo da correcção da viscosidade, já que a variação da temperatura da
água é relativamente pequena, obtém-se para limites do valor de Nue e consequentemente de
he, o seguinte,
51
4. Análise prévia dos resultados experimentais
3,7< Nue <6,1
230< he (W/m2K) < 380
Assim, pode ser estimada a temperatura exterior do tubo interior através do valor
experimental do calor recebido pela água
Twe = qag/( heAe)+ Tmag
(4.5)
com Ae=πdeLp e Tmag =(Tage+Tags)/2
Sendo esse calor transferido por condução através da espessura da parede do permutador
é possível fazer uma estimativa da temperatura da parede interior do permutador.
A resistência à condução pode ser calculada tendo em atenção a condutibilidade térmica
do aço inox, k= 45 W/mK, e a espessura da parede,
Rcond =
ln(d e / d i )
2 kπ L
(4.6)
O valor obtido foi de 4,31x10-4 ºC/W, e então,
Twi = Twe+ qagRcond
O que se verifica é que Twi ≅ Twe ≅ Tw
Conhecendo então, uma estimativa da temperatura da parede pode passar-se ao cálculo
das correcções das temperaturas lidas pelos termopares, devido ao efeito de radiação.
4.2.2 Efeito de radiação
De acordo com Çengel (1998), a temperatura de um determinado meio não é
necessariamente a indicada pelo aparelho de medida. Quando um termopar é colocado num
determinado meio, a transferência de calor dá-se por convecção entre o meio e o termopar até
que este atinja uma temperatura de equilíbrio. No entanto, quando o sensor está rodeado por
superfícies a temperaturas diferentes da do meio, é necessário contabilizar o efeito de
52
4. Análise prévia dos resultados experimentais
radiação, que leva a que a temperatura indicada pelo termopar não seja necessariamente a
temperatura real.
No caso concreto deste trabalho os termopares estão inseridos numa conduta cilíndrica
de 54,5 mm de diâmetro interno, onde circula ar quente, cujas paredes se encontram a uma
temperatura diferente da do meio. O equilíbrio na ponta dos diversos termopares será atingido
quando o ganho de calor por convecção igualar as perdas por radiação (ou vice-versa).
O termopar que está inserido na entrada do permutador fica rodeado pela parede de
membrana cuja temperatura é conhecida, e pela parede imediatamente abaixo que
corresponde à zona do leito. Neste caso, considera-se que a temperatura dessa parede é a
mesma da do leito e portanto a correcção a fazer será obtida pelo seguinte balanço,
′ tp−w
htp (Tarreal − Ttp ) = qrad
(4.7)
em que:
htp –coeficiente de convecção do termopar;
Tarreal- temperatura real do ar;
Ttp- temperatura lida pelo termopar;
q´radtp-w- fluxo de radiação trocado entre o termopar e a parede
Considerando que apenas há troca de calor por radiação para a parede membrana, já que
a parede na zona do leito pode ser considerada à temperatura do leito, e que a área do
termopar é muito pequena relativamente à área do permutador, o calor transferido por
radiação será dado por:
´
q radtp−w
σ (Ttp4 − Tw4 )
=
1 − ε tp
1
+
ε tp
Ftp − w
(4.8)
em que F tp-w, o factor de forma entre termopar e parede do permutador, é igual a 0,5.
Deste modo, e considerando que εtp = 0,9 (aço a 800K), o valor da temperatura real será
dado por:
Tarreal = Ttp +
0, 47σ (Ttp4 − Tw4 )
htp
(4.9)
53
4. Análise prévia dos resultados experimentais
Para o termopar que está situado na saída do permutador, a troca de calor por radiação
dá-se toda para uma parede a temperatura constante. Neste caso o balanço de energia é o
seguinte,
htp (Tarreal − Ttp ) = ε tpσ (Ttp4 − Tw4 )
(4.10)
Tarreal = Ttp +
ε tpσ (Ttp4 − Tw4 )
htp
em que as temperaturas são em Kelvin; htp é o coeficiente de convecção entre o ar e o
termopar que tem de ser estimado, e, Ttp é o valor da temperatura lida pelo termopar.
Estimativa do valor de htp
Para poder estimar este coeficiente recorreu-se a correlações empíricas apropriadas, ou
seja, aquelas que estimam coeficientes de convecção no caso de cilindros expostos a um
fluido com o eixo perpendicular ao escoamento. De acordo com Çengel (1998), a correlação
proposta é a seguinte:
Nutp = C Retpm Pr1/ 3
(4.11)
C e m são constantes empíricas e que dependem do valor de Retp. Como nas várias condições
de operação Retp situou-se entre 4 e 10, os valores destas constantes foram:
C = 0.911; m =0,385.
As propriedades são avaliadas à temperatura média entre o fluido e a parede interior do
permutador onde está inserido o termopar.
Os valores de Retp assim como de Nutp são calculados com o diâmetro do termopar. O
processo é então iterativo, uma vez que para avaliar a temperatura média é necessário
conhecer a temperatura real do fluido, que não é necessariamente a lida pelo termopar devido
ao efeito de radiação.
Conhecendo o valor de htp é então possível calcular as temperaturas reais do ar, na
entrada e saída do permutador.
54
4. Análise prévia dos resultados experimentais
4.3 Coeficiente de transferência de calor de um leito fluidizado borbulhante para um
permutador de parede membrana.
Como já foi referido existe muita literatura Científica sobre transferência de calor em
leitos fluidizados. No entanto, as várias correlações encontradas tendo em atenção os
diferentes mecanismos de transferência de calor envolvidos, e as contribuições dadas por gás
e partículas, são sempre obtidas em condições de operação diferentes das ocorridas neste
trabalho experimental. A maior parte dos estudos diz respeito a leitos fluidizados circulantes
havendo por isso um fluxo constante de sólidos na zona de transferência de calor, como por
exemplo os apresentados por Rhodes (1989) e por Wirth (1995). Há também outros estudos,
nomeadamente o de Al-Busoul (2002), que se refere à transferência de calor para provetes
introduzidos em leitos fluidizados.
De acordo com Bi and Grace (2000) há três fenómenos a considerar na transferência de
calor em leitos fluidizados quando estes constituem a zona de transferência de calor:
transferência de calor gás-partícula; transferência de calor partícula – partícula; transferência
de calor entre a suspensão e a superfície de transferência de calor. Os coeficientes de
transferência de calor gás-partícula tendem a ser bastante baixos uma vez que os gradientes
térmicos que existem entre os espaços vazios e a fase densa são pequenos devido à grande
área superficial das partículas. A transferência de calor por condução partícula-partícula,
devido aos choques interparticulares, é também em geral desprezável. Então, e de acordo com
o mesmo autor, o estudo limita-se neste caso à transferência de calor da suspensão para a
parede interna do permutador. Este último estudo pode ser analisado da seguinte maneira:
- o movimento convectivo das partículas transporta consigo calor por convecção desde o
leito até à superfície de transferência de calor - convecção devido às partículas;
- convecção devido ao movimento do gás através do leito;
- radiação leito - parede.
A importância de cada uma destas componentes depende das propriedades das partículas
e das condições de operação. Existem mapas de temperatura do leito em função do diâmetro
das partículas propostos por alguns autores, nomeadamente por Liann-Shih (1998), que
delimitam as zonas onde a contribuição de cada uma das componentes se torna mais
significativa. Esses mapas são no entanto feitos para partículas com diâmetros muito superiores
aos usados neste trabalho, pelo que não são aqui apresentados. No entanto, mostram que a
radiação se torna significativa acima de 600 ºC para qualquer tamanho de partículas, que a
55
4. Análise prévia dos resultados experimentais
componente de convecção devido ao gás aumenta com o tamanho das partículas, enquanto
que a influência da convecção, por parte das partículas, diminui com o aumento do tamanho
das mesmas.
Há autores que apresentam correlações em termos de grupos adimensionais para estimar
o coeficiente global de transferência de calor. As correlações que se encontraram,
nomeadamente as propostas por Bak et al (1989), num artigo de revisão de Bi and Grace
(2000), são do tipo:
Nu = a ArbRec
e cobrem condições de regime turbulento no leito conduzindo a coeficientes de transferência
de calor entre 40 a 370 W/m2K. As condições de operação presentes neste trabalho
corresponderam a regime borbulhante no leito e conduziram a coeficientes de transferência de
calor muito mais baixos.
No caso concreto deste trabalho as condições de operação conduziram, para todas as
granulometrias, a leitos fluidizados borbulhantes que se caracterizam por algum espalhamento
de partículas devido ao excesso de gás relativamente à velocidade mínima de fluidização.
Deste modo, as partículas atingiam a zona de transferência de calor que é constituída por um
permutador de parede membrana colocado acima do leito.
O estudo dos mecanismos de transferência de calor envolvidos, na taxa total de
transferência de calor para a água, tendo em consideração o espalhamento das partículas, é de
algum modo inovador. Assim sendo, e fazendo uma analogia com o encontrado em
bibliografia, o coeficiente global de transferência de calor do lado do leito, determinado
experimentalmente, vai ser entendido como um somatório de três parcelas consideradas
independentes:
- a convecção devido ao escoamento ascendente do gás - hgc;
- a radiação da superfície e paredes do leito para a zona de transferência de calor- hradL;
- a contribuição das partículas devido ao espalhamento - hpc
sendo assim,
hglo = hgc+ hradL + hpc
(4.12)
Esta última contribuição tem uma influência directa na taxa de transferência de calor
devido às partículas que atingem a zona de transferência de calor, mas também
56
4. Análise prévia dos resultados experimentais
indirectamente, devido às perturbações que provoca no perfil de velocidades e ainda às
alterações que induz na transferência de calor por radiação, uma vez que o espalhamento das
partículas altera o factor de forma de radiação do modelo que vai ser apresentado.
Deste modo, analisando os parâmetros fundamentais na transferência de calor face às
condições operatórias, e às dimensões das partículas usadas, vai-se tentar encontrar uma
correlação, expressa em termos adimensionais, que permita estimar o melhor possível o
coeficiente global de transferência de calor, nesta primeira fase que corresponde à ausência de
combustão. É também importante encontrar uma correlação para estimar o coeficiente global
na presença da combustão do propano e por fim uma correlação global que permita
correlacionar os dados experimentais com e sem combustão.
Para este efeito e apesar das condições operatórias serem diferentes das encontradas em
bibliografia foi feita uma pesquisa bibliográfica para tentar encontrar os grupos adimensionais
mais adequados à correlação que se procura.
4.3.1 Coeficiente de transferência de calor devido à convecção do gás - hgc
A determinação do coeficiente de transferência de calor por convecção devido ao gás foi
feita recorrendo a uma das correlações empíricas das muitas que existem em bibliografia,
nomeadamente as apresentadas por Çengel (1998) e por Ozisik (1985). O estudo da
transferência de calor por convecção forçada no interior de tubagens foi já largamente
aprofundado, e portanto, foi apenas necessário encontrar a correlação cujos limites de
aplicabilidade correspondam às condições de operação presentes. Neste caso o regime de
escoamento é laminar:
200 < Rear < 400
e face às equações já mencionadas para cálculo dos comprimentos de entrada, Lh e Lt, obtevese para todas as granulometrias usadas, os seguintes valores,
0,6 < Lh(m) < 1 e 0,3 < Lt(m) < 0,5
57
4. Análise prévia dos resultados experimentais
A zona de transferência de calor é também uma zona de entrada, em que a camada limite
hidrodinâmica e a camada limite térmica se encontram ambas em desenvolvimento. Para além
destas condições foi também considerada a situação de temperatura da parede constante:
Tw = constante
A correlação que permite estimar o valor de Nu para escoamento laminar em condutas
cilíndricas, na região de entrada, para desenvolvimento simultâneo e temperatura de parede
constante é a equação proposta por Hausen apresentada por Ozisik (1985):
Nu f = 3, 66 +
0, 0668Gz
1 + 0, 04Gz
2
(4.13)
3
válida para: Rear< 2100
Gz = RePrdi /Lp < 100
com propriedades do fluido avaliadas à temperatura do filme, Tf .
No entanto, tendo consciência que a convecção natural é um fenómeno sempre presente
no estudo da transferência de calor por convecção, foi preciso analisar com algum cuidado a
sua importância relativa no âmbito deste trabalho. É que as condições operatórias
corresponderam sempre a baixos caudais de gás e a grandes diferenças de temperatura entre
gás e parede.
O escoamento ascendente correspondeu a um fluxo de gás que vai arrefecendo numa
conduta onde se considerou a temperatura da parede constante, sendo esta necessariamente
inferior à temperatura no seio do gás. Assim sendo, vão-se gerar correntes de convecção
natural no sentido descendente da conduta. Este é o caso típico de transferência de calor em
que as duas correntes de convecção têm sentidos de circulação opostos. Este fenómeno vem
necessariamente alterar o perfil de velocidades junto à parede e consequentemente criar aí
diferentes gradientes térmicos. Como consequência, a taxa de transferência de calor do gás
para a parede do permutador vai ser alterada e por conseguinte o coeficiente de convecção
previsto pela equação 4.13, também poderá ser alterado.
O primeiro passo foi então procurar critérios gráficos ou equações, que permitissem
comparar a grandeza dos coeficientes de convecção natural e forçada e assim assegurar a
importância relativa de cada mecanismo nas condições operatórias. O parâmetro que aparece
associado a esta comparação é de acordo com Çengel (1998):
58
4. Análise prévia dos resultados experimentais
Gr
Re2
e o critério é o seguinte:
-
Gr
< 0,1 ⇒ Convecção natural é desprezável;
Re 2
- 0,1 <
-
Gr
< 10 ⇒ Convecção natural e forçada devem ser de considerar;
Re2
Gr
> 10 ⇒ Convecção forçada é desprezável.
Re2
Apesar de estes limites de natureza empírica, serem apenas uma indicação da
importância relativa de cada tipo de convecção, e corresponderem a situação de escoamento
desenvolvido, a gama deste parâmetro para as condições experimentais situou-se entre,
3<
Gr
< 13
Re2
o que permite assegurar que nenhum dos fenómenos de convecção deve ser aqui ignorado.
Estando nestas condições, vários autores nomeadamente, Churchill (1976), Behzadmchr
(2003), entre outros, propõem o cálculo do valor de um número de Nusselt combinado. Neste
caso concreto de escoamento laminar e de correntes de convecção que circulam em sentidos
opostos, o valor desse número de Nusselt combinado será sempre inferior ao calculado
considerando apenas a convecção forçada. De acordo com Churchill (1976) e também com o
proposto por Çengel (1998), uma das expressões para efectuar esse cálculo é:
Nucom = 3 Nu 3f − Nun3
(4.14)
Para poder usar esta expressão é então necessário encontrar correlações empíricas para o
caso de convecção natural em cilindros verticais com temperatura da parede constante e
inferior à temperatura média do fluido. Depois de uma pesquisa exaustiva, não se encontrou
qualquer correlação que satisfizesse as condições acima mencionadas.
Optou-se então por considerar apenas o valor de Nu previsto pela equação 4.13, já
referida para convecção forçada, tendo consciência que esse valor será com certeza um valor
calculado por excesso. Este facto, vai conduzir a que os valores obtidos para os coeficientes
de convecção devido às partículas hpc, sejam necessariamente mais baixos do que os valores
reais. Assim, a importância da contribuição do leito borbulhante para a transferência de calor
59
4. Análise prévia dos resultados experimentais
para o permutador de membrana poderá ser mais relevante do que aquela que aqui se vai
determinar.
4.3.2 Coeficiente de transferência de calor por radiação do leito para o permutador-hradL
A maior parte dos modelos encontrados em bibliografia dizem respeito à transferência
de calor por radiação em leitos fluidizados circulantes. De acordo com Al-Busoul (2002),
nessa situação a radiação terá importância para temperaturas superiores a 700 ºC no caso de
leitos com baixa densidade. Então, e segundo este mesmo autor, o modelo de radiação
previsto trata a parede do leito – emissividade εw – e suspensão de partículas – emissividade εs
– como duas placas paralelas de igual área. Segundo este modelo o coeficiente de radiação
será dado por,
hradL =
σ (T 4s −Tw4 )
 1

1
 ε s + ε w − 1  [Ts − Tw ]
(4.15)
Basu (1996) apresenta um trabalho em que faz referência a uma proposta de Grace
(1982), que refere que a emissividade da suspensão pode ser substituída pela emissividade de
uma nuvem de partículas calculada pela relação
ε c = 0, 5(1 + ε part )
(4.16)
em que:
εc é a emissividade da nuvem de partículas;
εpart é a emissividade das partículas.
Esta opção conduz a valores de εc entre 0,85 e 0,95
De acordo com as condições experimentais presentes, este modelo não é de maneira
nenhuma adequado. Mesmo no caso de se estar perante a combustão do propano, em que
devido às explosões se verificou algum arrasto de partículas ao longo da zona de transporte,
nunca se está numa situação de leito fluidizado circulante. É então necessário arranjar um
modelo de radiação, entre o leito borbulhante e as paredes do permutador, que permita
quantificar a contribuição deste mecanismo, calculando assim o coeficiente de radiação hradL.
60
4. Análise prévia dos resultados experimentais
O modelo proposto considera a troca de calor entre duas superfícies: o leito e a parede
do permutador. Neste caso, a zona do leito é o conjunto formado por duas superfícies: a
superfície cilíndrica do leito (A1), que corresponde a um disco de diâmetro igual ao diâmetro
da coluna, e a superfície 2, que corresponde à parede lateral abaixo da 1ª flange e que tem
altura l2 (A2). Todo este conjunto é considerado para efeitos de cálculo à mesma temperatura
que é a temperatura do leito. O esquema das superfícies consideradas para o modelo referido é
apresentado na Figura 4.5.
Permutador
AP
AL=A1+A2
P’
AL =πdi2/4+πdil2
l2
Ap = πdiLp
Ap´ = πdi2/4
A1
Leito
Figura 4.5 Esquema para identificação das superfícies envolvidas na troca de calor por radiação
Para encontrar a expressão que permita calcular a troca de calor entre as superfícies
mencionadas é apenas necessário saber o valor do factor de forma deste leito composto, para
o permutador, FL-p.
Para poder calcular o referido factor de forma considerou-se a superfície imaginária P´
referida na Figura 4.5. Assim, pode-se dizer o seguinte:
FL-p´ = FL-p
(4.17)
Além disso, como toda a radiação que chega às paredes do permutador vem do leito
então, Fp-L =1 e passou obrigatoriamente por P´, pelo que também FP´- L =1. Aplicando agora a
lei da reciprocidade obtém-se:
FL-p´x AL = FP´- L x AP´ ⇒ FL-p´ = (AP´/AL) x 1
(4.18)
61
4. Análise prévia dos resultados experimentais
Neste caso, sendo 420 mm a altura do distribuidor à flange e considerando um valor
médio para a altura do leito de 100 mm, o valor de l2 é de 320 mm. Pode-se assim determinar
o factor de forma pretendido, e tendo em conta a equação 4.18 e a 4.17, o resultado é:
FL-p = 0,04
O circuito térmico equivalente à troca de calor por radiação entre as superfícies
mencionadas pode ser representado do seguinte modo:
TL
RP
Resp
RL
Tw
Figura 4.6 Circuito térmico equivalente para a troca de calor por radiação entre a zona do leito e o
permutador, RL – resistência de radiação do leito; Resp- Resistência espacial de radiação;
RP- Resistência de radiação do permutador.
De acordo, com este circuito, o calor transferido por radiação pode ser calculado pela
equação:
σ (TL4 − Tw4 )
= hradL Ap (TL − Tw )
(4.19)
1− ε p
1− εL
1
; Resp =
; Rp =
ALε L
AL FL − p
Apε p
(4.20)
qradL =
∑R
i
em que :
RL =
Tendo em atenção tabelas de valores de emissividades de diferentes materiais, e que
toda a coluna é de aço inoxidável estando a zona correspondente ao leito muito oxidada, os
valores de emissividade considerados foram:
εL =0,9; εp =0,8
A equação que vai então permitir o cálculo de hradL é então:
62
4. Análise prévia dos resultados experimentais
hradL =
σ (TL4 − Tw4 )
Ap (TL − Tw ) ∑ Ri
(4.21)
4.3.3 Coeficiente de transferência de calor devido às partículas – hpc
Nos ensaios feitos na ausência de combustão não se notou qualquer variação da pressão
do leito, o que significa que os caudais de ar usados não foram suficientes para provocar o
transporte e arrasto de partículas através da zona de transferência de calor. No entanto, as
condições de operação corresponderam sempre a um excesso de gás relativamente à
velocidade mínima de fluidização, o que provocou a formação de bolhas que sobem através
do leito e arrastam consigo partículas. Estas bolhas, que rebentam à superfície do leito,
provocam projecção de partículas, podendo as mais finas ser arrastadas pela corrente de gás e
as outras voltarem ao leito. Sendo assim, é natural que não haja alteração da pressão do leito.
Ao contrário, nos ensaios feitos com a presença do propano e portanto em situação de
combustão, notou-se uma variação da pressão do leito para as três menores granulometrias,
não variando para o caso de dp=282,5 µm e dp=357,5 µm. Isto significa que quando o leito é
formado pelas partículas mais pequenas se consegue efectivamente um arrasto das mesmas.
Este fenómeno, de movimento de partículas, deve influenciar de algum modo a taxa de
transferência de calor na zona de transporte, e deverá ser tanto mais importante quanto menor
for a dimensão das partículas. Pois se por um lado o excesso de gás é maior, para as mesmas
condições de operação, por outro lado, a percentagem de partículas mais finas será também
maior.
Como se referiu este movimento aleatório das partículas pode influenciar a taxa de
transferência de calor da seguinte forma:
- As alterações hidrodinâmicas no escoamento do gás quando este atravessa o leito vão-se
reflectir ao longo da zona de transferência de calor, tendo como consequência
perturbações no perfil de velocidades junto à parede, o que influencia os gradientes
térmicos aí criados e portanto a convecção devido ao gás;
- O facto da superfície do leito não se manter, como no caso de leitos fluidizados, como
um disco perpendicular à secção recta da coluna, provoca alterações no modelo de
radiação proposto;
- As partículas finas que atinjem a zona de transporte, ao chocarem com a parede do
permutador transferem calor por condução.
63
4. Análise prévia dos resultados experimentais
São todos estes aspectos que se pretendem contabilizar no cálculo do coeficiente de
convecção das partículas hpc
Na ausência de modelos que se adaptem às condições inerentes a este trabalho, este
coeficiente vai ser calculado tendo em atenção os valores experimentais obtidos para o
coeficiente global de transferência de calor hglo, pela relação:
hpc= hglo – ( hgc + hradL )
(4.22)
No entanto, depois de obtidos estes valores, numa primeira fase sem combustão e numa
segunda fase já na presença da reacção, o objectivo será encontrar uma correlação baseada em
grupos adimensionais adequados, que permita ajustar o melhor possível os resultados obtidos.
Segundo um estudo feito por Molerus (1995), relativamente à influencia do movimento
migratório de partículas na transferência de calor entre as mesmas e superfícies imersas em
leitos fluidizados, verificou-se que para partículas com dp< 100 µm o termo convectivo
devido às partículas era dominante relativamente à convecção devido ao gás. Um dos grupos
adimensionais que está relacionado com a importância relativa destes dois factores é o
número de Arquimedes. Segundo a mesma fonte, para Ar < 100 prevalece o efeito das
partículas; para 105 < Ar < 108 prevalece a convecção devido ao gás. Isto permite concluir
que o tamanho das partículas influencia a transferência de calor, e este efeito, pode e deve ser
relacionado com o excesso de gás expresso de forma adimensional, ou seja com o seguinte
parâmetro:
v0 − vmf
vmf
Embora as condições experimentais deste trabalho não correspondam às consideradas
no estudo de Molerus (1995), as correlações que se irão estudar para o cálculo de hpc devem
incluir pelo menos o grupo adimensional atrás referido. Este grupo, é o que quantifica de
algum modo o maior ou menor espalhamento de partículas na zona do leito, e é esse o
principal fenómeno que interfere na transferência de calor de um leito borbulhante para um
permutador de parede de membrana.
64
4. Análise prévia dos resultados experimentais
4.4 Análise do calor trocado no primeiro permutador com combustão de propano
A combustão do propano, sendo uma reacção exotérmica é a grande fonte de calor para
o aquecimento dos gases. No entanto, como o permutador se encontra acima da zona de
reacção o balanço de energia à zona do permutador é o mesmo com e sem reacção.
Também nesta fase de ensaios, se constatou que o calor recebido pela água era sempre
superior à variação de entalpia dos gases de combustão que subiam ao longo do permutador, e
essa diferença é em alguns casos muito superior à que se obteve na ausência de combustão.
Tendo também como base o calor recebido pela água, é esse valor que vai permitir
calcular um coeficiente global de transferência de calor. Esse coeficiente vai permitir, do
mesmo modo que anteriormente, quantificar todos os fenómenos envolvidos na transferência
de calor deste sistema. Assim, vai também ser entendido como um somatório de três parcelas
consideradas independentes e que já foram referidas:
- a convecção devido ao escoamento ascendente do gás, hgc;
- a radiação da superfície e paredes do leito para a zona de transferência de calor, hradL;
- a contribuição das partículas devido ao espalhamento, hpc.
No entanto, pelo facto de se estar perante uma reacção de combustão, em que os
produtos resultantes participam no processo de radiação entre o leito e a superfície do
permutador, o termo correspondente a hradL, tem se ser bem analisado, levando em
consideração esta questão.
As diferenças fundamentais no tratamento dos dados relativamente à situação de
ausência de combustão, foram as seguintes:
As propriedades físicas dizem agora respeito a uma mistura de gases de combustão e
não ao ar. Deste modo, como não se analisou em termos de composição os gases à saída
do reactor, a composição da mistura gasosa vai ser quantificada de acordo com a
estequiometria da reacção e do valor de r em cada ensaio.
De acordo com o apresentado por Macintyre (1988):
C3 H 8 +5(1 − d )(O2 + 3.76 N 2 ) → n1CO2 + n2CO + n3 H 2O + n4 H 2 + 5 × 3.76(1 − d ) N 2
(4.23)
sendo 1-d = 1/r
65
4. Análise prévia dos resultados experimentais
r=
em que
( A / C )est
( A / C )real
(4.24)
O valor de r experimental permite o acerto da reacção química, mas fazendo o balanço a
cada elemento tem-se quatro incógnitas e três equações. Há então três possibilidades:
a) exprimir três coeficientes em função do quarto;
b) desprezar a concentração de um dos produtos - válido quando xH2<< xCO, sendo xH2 e
xCO as fracções molares de hidrogénio e de monóxido de carbono, respectivamente;
c) arranjar uma 4ª equação.
Na falta de analisador para permitir saber correctamente a composição da mistura gasosa
optou-se por escolher a possibilidade c).
Estes cálculos são apresentados no Apêndice IV.
Os resultados da composição da mistura que se obtêm por esta via têm associados algum
erro, porque não se sabe até que ponto também existem na mistura gasosa, outros
hidrocarbonetos obtidos por pirólise do propano, já que se trabalha em condições de defeito
de ar. No entanto, devido ao facto de que a razão entre o caudal de ar e propano
estequiométrico, (A/C)est é da ordem de 15, as propriedades da mistura não irão variar
grandemente com flutuações em r e no grau de complitude da reacção.
A parcela que corresponde à contribuição das partículas é neste caso não só devido ao
espalhamento, mas ao arrasto de partículas que são transportadas ao longo da zona de
transferência de calor. Como se pode verificar pela figura seguinte que corresponde a
uma das que vêm apresentadas no Capítulo 7, (nomeadamente à Figura 7.2) durante os
ensaios correspondentes às três granulometrias mais pequenas houve sempre uma
variação da pressão do leito.
66
4. Análise prévia dos resultados experimentais
12
PL (cm de H2O)
10
8
6
4
2
0
0
1000
2000
3000
4000
5000
tempo(s)
Figura 7.2.- Variação da pressão do leito versus tempo; dp=107,5 µm
Isto significou que as partículas que foram arrastadas não voltaram ao leito, e então, será
possível quantificar a taxa de elutriação das mesmas, usando os dados experimentais dos
gráficos de variação de pressão do leito com o tempo, como este da Figura 7.2.
Como já se referiu, deve ser analisado com mais cuidado o termo correspondente ao
calor transferido por radiação. Uma vez que existe uma reacção de combustão no leito,
e essa combustão se dá num meio redutor (defeito de ar), a mistura que escoa ao longo
da coluna é formada pelos produtos resultantes dessa reacção ou seja; CO2, H2O, N2,
CO, hidrocarbonetos não queimados (HC), além de possivelmente algum H2. De
acordo com Çengel (2003) e com William (1954), a existência de moléculas
assimétricas faz deste meio gasoso, um meio participante no que diz respeito à
radiação térmica. Deste modo, e ao contrário do que acontece com o ar que é formado
por O2 e N2 e portanto considerado não participante, ou seja completamente
transparente à radiação térmica, este meio gasoso a temperaturas elevadas, absorve e
emite radiação. Isto complica consideravelmente a análise da radiação uma vez que
obriga a que se conheça a emissividade da mistura gasosa e a absortividade da mesma,
que terão de ter em conta correcções devido à presença das moléculas que interferem
na radiação. De acordo com Çengel (2003), as expressões que permitem o cálculo de
εg e αg são:
ε g = ε H O + ε CO + ε CO − ∆ε
2
2
α g = α H O + α CO + α CO − ∆α
2
(4.25)
2
67
4. Análise prévia dos resultados experimentais
em que εg e αg, são função das pressões parciais de cada componente que interfere na
radiação, da temperatura do gás e de um parâmetro geométrico definido como percurso médio
da radiação, Lmr. De acordo com expressões propostas por Çengel (2003) para cálculo deste
parâmetro, e uma vez que se pretende determinar a transferência de calor do leito para a
parede do permutador, tendo em consideração o meio participante, a expressão usada deve
ser,
Lmr = 0,65di
(4.26)
Por outro lado, ∆ε e ∆α representam as correcções que é necessário fazer a εg e a αg
pelo facto dos componentes poderem emitir radiação em bandas de comprimento de onda
sobrepostos. Todos estes valores podem ser calculados através de gráficos apresentados por
Çengel (2003), a partir do conhecimento prévio da composição da mistura, em termos de
pressões parciais dos seus componentes. Tendo em conta a composição da mistura gasosa que
vem apresentada no Apêndice IV, verifica-se que a fracção molar de N2 é a que está presente
em maior quantidade, sendo as fracções das moléculas assimétricas como CO2, H2O e CO ,
cerca de 10 vezes mais pequenas. Deste modo, é natural que a contribuição do meio
participante para a transferência de calor por radiação seja desprezável, e, nesse caso, o
modelo que melhor permitirá calcular a taxa de transferência de calor por radiação do leito
para a parede seja novamente o modelo apresentado na secção 4.3.2. Se assim for então hradL
será também calculado pela equação 4.21, mesmo no caso dos ensaios com combustão.
Contudo, para que se possa confirmar as hipóteses
acima apresentadas, é preciso quantificar o valor de hradL, tendo em atenção a presença do
meio participante. O método que se vai usar é apresentado em Çengel (2003) e proposto por
Hottel. Este autor considera que a superfície com a qual o gás participante troca calor por
radiação é uma superfície negra. Desta forma, e depois de calculados os valores de εg e αg,
calcula-se o calor de radiação devido ao meio participante entre o leito e o permutador pela
expressão,
(
qrmp = Apσ ε g Tg4 − α g Tw4
)
(4.27)
como Tg>> Tw, o segundo termo desta equação pode ser desprezável.
Segundo o mesmo autor, para as câmaras de combustão que têm em geral valores de
emissividade maiores que 0,7, a aproximação feita de as considerar como corpo negro não se
afasta muito da realidade. Contudo, propõe uma correcção que é a seguinte,
68
4. Análise prévia dos resultados experimentais
qrmp =
ε p +1
2
Apσε g Tg4
(4.28)
Desta forma o valor do coeficiente de transferência de calor por radiação devido ao meio
participante será dado por,
hrmp =
σε g Tg4
(Tg − Tw )
×
ε p +1
2
(4.29)
Há então duas hipóteses para o cálculo do calor por radiação e por conseguinte para o
cálculo de hradL:
- considerar o modelo já proposto na secção 4.3.2, que será então válido par todos os
ensaio com e sem combustão;
- considerar o método de Hottel, que ao introduzir o parâmetro Lmr, tem em conta o calor
de radiação trocado entre o leito e a parede, em presença de um meio participante.
Esta análise de escolha do método mais adequado será feita no Capítulo 9.
69
5.Transferência de calor na ausência de combustão
5.Transferência de calor na ausência de combustão
5.1 Caracterização do tipo de regime no leito de partículas
Antes de passar ao estudo da transferência de calor num leito de partículas é essencial
conhecer o tipo de regime que caracteriza esse mesmo leito, nas condições de operação. Essa
análise será feita neste capítulo, começando por caracterizar o regime do leito na ausência de
combustão.
A grandeza que permite caracterizar o tipo de regime num leito de partículas é o valor
da pressão. A variação do diferencial de pressão entre o leito e a zona de transporte, com a
velocidade superficial do gás, permite distinguir vários regimes de fluidização com
características distintas, que segundo Rhodes (1996) podem ser divididos em:
- Fluidização borbulhante;
- Fluidização transitória;
- Fluidização turbulenta;
- Fluidização rápida ou circulante
Na Figura 5.1, é evidente a variação de pressão que ocorre em cada regime em função
da velocidade superficial. Mostra-se também as características do leito nas diversas fases de
escoamento
71
Densidade do leito
Variação da pressão
5.Transferência de calor na ausência de combustão
vc
vk
Velocidade superficial do gás
Figura 5.1 Variação da pressão num leito fluidizado em função da velocidade superficial do gás.
Zonas de transição caracterizadas pela velocidade vc e vk., Rhodes (1996).
Nesta figura distinguem-se dois valores para a velocidade superficial:
- velocidade critica - vc - é uma indicação da mudança de fluidização borbulhante para
fluidização de transição. Para este valor de velocidade a altura do leito é máxima;
- velocidade de transição - vk - marca o início da fluidização turbulenta. Nesta fase
atinge-se a altura mínima do leito.
No artigo de revisão de Bi and Grace (2000), são referidos muitos autores,
nomeadamente Bi and Fan (1992), que consideram ainda uma velocidade de transporte, vtr
que marca a transição de fluidização turbulenta para fluidização rápida, mas mostram através
de dados experimentais e das correlações empíricas que apresentam, que a velocidade de
transição é praticamente igual a essa velocidade de transporte das partículas sólidas.
Na Figura 5.2 mostra-se também, os limites de velocidade de gás para os quais ocorre
mudança do regime de escoamento no leito.
72
5.Transferência de calor na ausência de combustão
Areia
Prms [mm água]
Densidade do leito
vc
vk
vtr
Velocidade superficial
Figura 5.2 Variação da raiz quadrada da pressão e da densidade do leito com a velocidade superficial
do gás de acordo com vários regimes: B – borbulhante; Tr – Transição; T – Turbulento,
Rhodes (1996) reproduzido por Horio et al (1992).
Apesar de todos estes estudos, há ainda autores que não distinguem a zona de transição,
e, consideram, que a partir do valor da velocidade crítica, se entra na zona turbulenta. Deste
modo, e dadas as condições de operação inerentes ao trabalho experimental vai-se procurar
caracterizar o regime do leito no que diz respeito apenas à velocidade crítica, e à velocidade de
transporte, apresentando-se correlações empíricas para que se possam estimar estes dois
valores de velocidade e compará-los com o valor da velocidade superficial do gás nas
condições de operação.
5.1.1 Determinação da velocidade crítica - vc
Vários autores, nomeadamente Bi and Grace (2000), reúnem um conjunto de estudos
feitos por outros autores que analisam os parâmetros de que depende esta velocidade.
- Altura estática do leito - para leitos considerados rasos – hmf/di <2 - e para
partículas do grupo B e D, Canada et al (1978) e Dunham et al (1993) verificaram
que vc aumentava com o aumento da altura estática do leito;
- Diâmetro da coluna – Segundo Cai (1989) este parâmetro só afecta a velocidade
crítica quando se têm colunas com diâmetro inferior a 0,2 m. Neste caso o
diâmetro afecta o tamanho e velocidade de subida das bolhas e o seu aumento
conduz a uma diminuição da velocidade crítica;
- Tamanho e densidade das partículas – quanto maior for o tamanho e a
densidade maior será a velocidade crítica;
73
5.Transferência de calor na ausência de combustão
- Temperatura - poucos estudos foram feitos relativamente à influência da
temperatura no valor de vc. Cai et al (1989) verificou que a velocidade crítica
aumentava com o aumento da temperatura a pressão constante. Este facto, prendese certamente com a diminuição da densidade e aumento da viscosidade da fase
gasosa.
Há várias autores a apresentarem correlações empíricas para estimar o valor da
velocidade crítica, mas uma das que dá melhor previsão, além de entrar com o efeito da
temperatura, é a obtida por Cai et al (1989) e que vem apresentada no artigo de Bi and Grace
(2000), acima mencionado,
 µ g 20 
=

g × d p  µ g 
vc
0,2
 0, 211 0, 00242 1 0,27  ρ g 20   ρ p − ρ g
 0,27 +

 

di1,27 
 di
 ρg   ρg
  di
 
 dp

 
 
0,27
(5.1)
A velocidade crítica, vc determinada por esta correlação é uma indicação da mudança de
regime, de fluidização borbulhante para fluidização turbulenta. A partir deste valor pode-se
calcular o valor de Rec, baseado no diâmetro da partícula.
5.1.2 Determinação da velocidade de transporte – vtr
Recorre-se também a correlações que permitem determinar a velocidade de transporte,vtr velocidade esta, que marca o início da fluidização rápida ou circulante. São vários autores a
apresentarem correlações empíricas, mas é difícil saber a que melhor estimativa dá no caso
deste trabalho experimental, pois, as condições experimentais envolvidas são bastante
diferentes no que diz respeito, ao diâmetro e altura da coluna. Optou-se então por escolher a
proposta por Chehbouni et al (1995), apresentada no artigo já referido de Bi and Grace
(2000), pois além de ser mais recente entra com o efeito do diâmetro da coluna.
Retr = 0.169 Ar 0,545 ( d i / d p )
sendo:
74
0,3
(5.2)
5.Transferência de calor na ausência de combustão
Retr =ρg vtrdp/µg e Ar = d 3p g ρ g ( ρ p − ρ g ) / µ g2
Este valor do número de Arquimedes é função unicamente das propriedades do gás, e da
dimensão das partículas usadas. Quando a temperatura aumenta o valor de Arquimedes
diminui pelo efeito da diminuição da massa volúmica do gás, mas sobretudo pelo aumento da
viscosidade dinâmica, variável que aparece ao quadrado.
5.1.3 Comparação dos valores de Ret, Rec, Retr e Rep em função de Ar para as diferentes
condições operatórias.
Nesta fase do trabalho em que os ensaios são feitos sem ocorrência de reacção, a gama
de operação para temperatura do leito e caudal de ar é, como já foi referido no Capítulo 3, a
seguinte:
400 < TL(ºC) < 700
0,82< mar (kg/h) < 1,5
São estas, as condições de operação, para as quais se define o número de Reynolds da
partícula, calculado a partir da velocidade superficial do ar. Todos os valores de Reynolds,
Rep, Rec, Retr, são então definidos em termos do diâmetro da partícula , das propriedades
físicas do ar às várias temperaturas do leito, e da velocidade v0, vc, vtr respectivamente. É
também pertinente o cálculo de Ret - Reynolds referido à velocidade terminal de uma
partícula isolada.
A comparação dos vários valores de Re obtidos, pode ser visualizada nas figuras que a
seguir se apresentam. Cada gráfico diz respeito a um tamanho de partículas, uma vez que os
limites para o número Arquimedes, que é avaliado à temperatura do leito, correspondem a
gamas muito diferentes, consoante a granulometria. Esses limites são:
- dp=107,5 µm
↔ 6,5 < Ar < 14,9
- dp=142,5 µm
↔ 15,5 < Ar < 35,4
- dp=180 µm
↔ 32 < Ar < 72
- dp=282,5 µm
↔ 124 < Ar < 284
- dp=357,5 µm
↔ 251 < Ar < 574
75
5.Transferência de calor na ausência de combustão
A Figura 5.3 diz respeito aos resultados obtidos para as partículas de menor
granulometria, partículas com dp= 107,5 µm. De seguida apresentam-se as figuras
correspondentes aos restantes tamanhos.
12
Re
Re
Re
Rep,Ret ,Rec;Retr
10
8
6
Re tr
4
Re c
2
Ret
0
0
2
4
6
8
10
12
14
16
Ar
Resultados obtidos para Rep nas várias condições de operação
Figura 5.3 Valores para Rep, Ret, Rec, Retr em função de Ar, para dp=107,5 µm
Resultados obtidos para partículas com dp= 142,5 µm
12
Rep,Ret,Rec,Retr
10
8
Retr
6
4
Rec
2
Ret
0
0
5
10
15
20
25
30
35
40
Ar
Resultados obtidos para Rep nas várias condições de operação
Figura 5.4 Valores para Rep,Ret,Rec,Retr em função de Ar, para dp=142,5 µm
76
5.Transferência de calor na ausência de combustão
Resultados obtidos para partículas com dp= 180 µm
12
Rep,Ret,Rec,Retr
10
8
Retr
6
4
Rec
Ret
2
0
0
10
20
30
40
50
60
70
80
Ar
Resultados obtidis para Rep nas várias condições de operação
Figura 5.5 Valores para Rep,Ret,Rec,Retr em função de Ar, para dp=180 µm
Resultados obtidos para partículas com dp= 282,5 µm
30
Rep,Ret,Rec,Retr
25
20
Retr
15
10
Ret
Rec
5
0
0
50
100
150
200
250
300
Ar
Resultados obtidos para Rep nas várias condições de operação
Figura 5.6 Valores para Rep,Ret,Rec,Retr em função de Ar, para dp=282,5 µm
77
5.Transferência de calor na ausência de combustão
Resultados obtidos para partículas com dp= 357,5 µm
30
Rep, Ret, Rec, Retr
25
Retr
20
Ret
15
10
Rec
5
0
0
100
200
300
400
500
600
700
Ar
Resultados obtidos para Rep nas várias condições de operação
Figura 5.7 Valores para Rep,Ret,Rec,Retr em função de Ar, para dp=357,5 µm
Pela análise das figuras acima, verifica-se que para qualquer uma das granulometrias
usadas, seja qual for a temperatura do ensaio, 400< TL(ºC) < 700, e o caudal de gás de,
0,82 < mar(kg/h ) <1,5, as condições de escoamento no leito correspondem a um regime
borbulhante, pois, os valores de Rep são sempre inferiores a Rec. Contudo, pode-se constatar
que as condições de trabalho mais favoráveis em termos de possibilidade de transporte de
partículas são as que correspondem às partículas mais pequenas, aos ensaios correspondentes
aos caudais mais elevados e às temperaturas mais altas- números de Arquimedes mais baixos.
Para as duas granulometrias mais baixas, verifica-se também que apesar do leito apresentar
características de leito borbulhante, os valores de Rep são muito próximos e até ligeiramente
superiores aos valores de Ret, o que significa que para estas partículas existirá algum
transporte de sólidos que será arrastado pela corrente de gás.
Uma outra constatação importante é que à medida que o tamanho das partículas
aumenta, os valores de Ret vão-se aproximando dos valores de Rec, e para as duas
granulometrias maiores acontece até que os valores se invertem ou seja; Ret > Rec. Então, para
estes tamanhos maiores, a possibilidade de atingir condições de regime turbulento no leito não
implica necessariamente que se esteja com valores de Rep superiores aos valores de Ret.
Uma outra maneira de poder definir o tipo de regime no leito de partículas nas várias
condições de operação é analisando mapas disponíveis na literatura Científica. Há autores,
nomeadamente, Wen-Ching (2003) que refere um mapa de leitos fluidizados, apresentado por
78
5.Transferência de calor na ausência de combustão
Grace, onde se limitam os vários regimes do leito em função de dois parâmetros
adimensionais:
- dp* = Ar1/3
- v* = (v0-vmf)/(vt-vmf)
Esse mapa vem apresentado na Figura 5.8, e aí é assinalada a gama de trabalho
correspondente a v*, face às condições de operação para as várias granulometrias definidas
em termos do parâmetro dp*.
v*
dp *
Figura 5.8- Mapa de regime de fluidização num leito de partículas, Wen-Ching (2003)
Neste mapa, as linhas a) e b) indicam os limites usuais de trabalho para leitos
fluidizados borbulhantes, enquanto que as linhas c) e d) limitam as zonas de operação para
leitos circulantes. As áreas assinaladas nesta figura a diferentes cores correspondem à zona de
operação para as várias granulometrias, sendo assim,
dp=107,5 µm-cor de laranja;
dp=142,5 µm-verde;
dp=180 µm-azul;
dp=282,5µm-vermelho;
dp=357,5µm-rosa.
79
5.Transferência de calor na ausência de combustão
Mais uma vez, através da Figura 5.8, se pode confirmar as condições de borbulhamento
dos leitos formados para as diferentes granulometrias. Pela análise desta figura é também
evidente a grande diferença entre o grau de borbulhamento atingido pelas diferentes partículas
para as mesmas condições operatórias e até o facto de se poder atingir para as partículas de
dp=107,5 µm condições de fluidização turbulenta.
Estas características diferentes de borbulhamento vão influenciar a taxa de transferência
de calor para a água. Então, deve ser analisado o número de vmf´s, ou seja o quociente entre
v0/vmf, para cada granulometria na gama de operação. As figuras que se seguem, usando
gráficos de barras, pretendem representar e comparar as condições de operação que se
atingiram no leito em termos de v0/vmf, para as várias temperaturas, para os vários caudais de
ar e para os cinco tamanhos de partículas utilizados nos testes.
35
33
30
27
25
v0/vmf
22
20
18
16
16
15
13
9 10
10
13
11
9
4
5
0
3 3
107,5
180
142,5
282,5
5
3
2 2 3
357,5
dp(µ
µm)
0,82
1
1,25
1,5
Figura 5.9 Rácio v0/vmf para o caudal de ar 0,82 < mar (kg/h)< 1,5 e para TL = 400 ºC.
80
5.Transferência de calor na ausência de combustão
45
42
40
35
35
v0/vmf
30
25
28
23
20
20
20
17
16
15
11
13
11
13
10
5 6
3 4
5
4 4
2 3
0
142,5
107,5
180
282,5
357,5
dp(µm)
0,82
1
1,25
1,5
Figura 5.10- Rácio v0/vmf para o caudal de ar 0,82<mar(kg/h)<1,5 e para TL=500ºC.
40
34
35
30
28
v0/vmf
25
21
20
20
16
13
15
16
13
8
10
6
4 5
5
5
3 3 4
0
107,5
142,5
180
282,5
357,5
dp(µm)
0,82
1
1,25
1,5
Figura 5.11 Rácio v0/vmf para o caudal de ar 0,82<mar(kg/h)<1,5 e para TL=600ºC.
81
5.Transferência de calor na ausência de combustão
40
35
33
30
24
v0/vmf
25
19
20
19
16
15
15
10
5 6
8
5
5 6
3 4
0
107,5
142,5
180
282,5
357.5
dp(µ
µm)
0,82
1
1,25
1,5
Figura 5.12 Rácio v0/vmf para o caudal de ar 0,82<mar(kg/h)<1,5 e para TL=700ºC.
Como seria de esperar as partículas mais pequenas apresentam valores de v0/vmf muito
superiores a qualquer uma das outras. Além disso, com esta granulometria também se atingem
condições próximas das exigidas para o transporte das mesmas, ver Figura 5.3. Para as
partículas com dp=142,5 µm e dp=180 µm, apesar de apresentarem comportamentos muito
semelhantes em termos dos valores de v0/vmf, o arrasto conseguido é maior para as de
dp=142,5 µm, sobretudo nos caudais maiores e às temperaturas mais elevadas, ver Figura 5.4.
Para os dois tamanhos maiores de partículas, as diferenças em termos de regime do leito são
quase inexistentes, nunca se atingindo para nenhuma delas nas condições de operação,
situações próximas do arrasto, ver Figuras 5.6 e 5.7.
Uma outra constatação que se torna evidente nas Figuras 5.11 e 5.12 é que para
temperaturas do leito de 600ºC e 700 ºC, não foi possível trabalhar com toda a gama de
caudais de ar. Para dp=107,5 µm e temperatura do leito de 700 ºC, só se conseguiu atingir
condições de estado estacionário no caso de mar = 0,82 kg/h.
De acordo com o apresentado nestas figuras, a tabela que se segue pretende de alguma
maneira apresentar as condições de operação que permitiram para cada granulometria, atingir
condições de estado estacionário.
82
5.Transferência de calor na ausência de combustão
Tabela 5.1 Temperatura máxima atingida no leito para os diversos caudais de ar e diferentes
granulometrias
µm)
dp(µ
107,5
142,5
180
282,5
357,5
mar(kg/h)
Tmax (ºC)
0,82
700
1
660
1,25
550
1,25
550
≤1
700
1,25
600
1,5
500
≤1,25
700
1,5
500
≤1,25
700
1,5
600
≤1,5
700
5.2 Influência do caudal de água e da temperatura do leito na transferência de calor
A influência do caudal de água a escoar na camisa de arrefecimento foi estudada para as
diversas granulometrias de areia, para as diferentes temperaturas e impondo sempre um
caudal de ar de 1 kg/h. Também se analisou para alguns dos ensaios o calor residual que deve
ser entendido como o calor axial que se transfere para a água pelo próprio corpo do reactor.
Este calor, deve em princípio ser deduzido ao calor recebido pela água de forma a que se
contabilize unicamente o que vem de dentro do reactor (radiação, condução e convecção do
gás e das partículas). Como os ensaios foram feitos para as 5 granulometrias de areia, para
dois ou três caudais de água diferentes e para a temperatura de 400 ºC, 500 ºC, 600 ºC e
700ºC, o número de figuras a apresentar era demasiado extenso. Optou-se então, por referir
apenas 5 figuras representativas do universo de ensaios feitos. Em todas elas usou-se a cor
azul para representar os resultados obtidos para mag =35 kg/h; a cor vermelha para os
correspondentes a mag =73 kg/h e a cor amarela para os resultados obtidos no caso do de
mag =140 kg/h. Mais uma vez as primeiras figuras que se apresentam dizem respeito às
partículas de dp=107,5 µm
83
5.Transferência de calor na ausência de combustão
Partículas com dp=107,5 µm
Potência térmica (W) e TLºC)
600
500
TL
400
300
qag
200
qar
100
0
0
500
1000
1500
2000
2500
3000
tempo(s)
mag=73 kg/h
mag=140 kg/h
Figura 5.13 Variação da entalpia do ar e da agua para dois caudais de água distintos, no caso de
TL= 400 ºC, mar = 1 kg/h, PL=12 cm, vo/vmf = 22, dp=107,5 µm
Potência térmica (W) e TL(ºC)
1200
qag
1000
800
600
TL
400
qar
200
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
mag=35 kg/h
mag=73 kg/h
Figura 5.14 Variação da entalpia do ar e da agua para dois caudais de água distintos, no caso de
TL= 660 ºC, mar = 1 kg/h, PL= 13 cm, vo/vmf = 37, dp=107,5 µm
Para esta granulometria, e para mar= 1 kg/h, a temperatura máxima que se conseguiu atingir
foi de cerca de 660ºC.
84
5.Transferência de calor na ausência de combustão
Partículas com dp=142,5 µm
Potência térmica (W) eTL(ªC)
700
600
TL
500
400
qag
300
200
qar
100
0
0
500
1000
1500
2000
2500
3000
3500
tempo(s)
mag=35 kg/h
mag=73 kg/h
Figura 5.15 Variação da entalpia do ar e da agua para dois caudais de água distintos, no caso de
TL= 500 ºC, mar = 1 kg/h, PL= 16 cm, vo/vmf = 13, dp=142,5 µm
Partículas com dp=180 µm
Potência térmica (W) e TL (ºC)
900
800
TL
700
600
500
qag
400
300
200
qar
100
0
0
200
400
600
800
1000
1200
1400
1600
tempo(s)
mag=35 kg/h
mag=73 kg/h
mag= 140 kg/h
Figura 5.16 Variação da entalpia do ar e da agua para três caudais de água distintos, no caso de
TL= 700 ºC, mar = 1 kg/h, PL= 10 cm, vo/vmf = 19, dp=180 µm
85
5.Transferência de calor na ausência de combustão
Partículas com dp=282,5 µm
Potência térmica (W) e TL (ºC)
900
800
TL
700
600
500
400
qag
300
qar
200
100
0
0
500
1000
tempo(s)
mag=35 kg/h
1500
2000
mag=73 kg/h
Figura 5.17 Variação da entalpia do ar e da agua para dois caudais de água distintos, no caso de
TL= 700 ºC, mar = 1 kg/h, PL= 9 cm, vo/vmf = 6, dp=282,5 µm
Partículas com dp=357,5 µm
Potência térmica (W) e TL (ºC)
800
TL
700
600
500
400
qag
300
qar
200
100
0
0
500
1000
tempo(s)
mag=35 kg/h
1500
2000
mag=73 kg/h
Figura 5.18 Variação da entalpia do ar e da agua para dois caudais de água distintos, no caso de
TL= 700 ºC, mar = 1 kg/h, PL= 8 cm, vo/vmf = 4, dp=357,5 µm
86
5.Transferência de calor na ausência de combustão
Como
se pode constatar,
embora existam
algumas
oscilações
nas
curvas
correspondentes à variação de entalpia da água devido a oscilações no caudal de água, este
parâmetro não afecta o resultado obtido. Esta conclusão é válida para qualquer granulometria
e para qualquer temperatura do leito. Pelas figuras apresentadas pode-se também verificar que
a variação da entalpia do ar é praticamente constante com a temperatura imposta ao leito para
as várias granulometrias. Contudo, a quantidade de calor recebida pela água varia com a
granulometria e com a temperatura do leito. Para melhor poder comparar o que se acabou de
expor são apresentados nas tabelas que se seguem os resultados correspondentes à variação de
entalpia do ar e da água em termos de valores médios, considerando para esse cálculo os
valores obtidos apenas para o caudal de ar de 1kg/h e para os vários caudais de água. Os
valores que estiveram na base do cálculo dessa média são apresentados no Apêndice V.
Nestas tabelas que se apresentam é também feita referência à diferença de entalpia das duas
correntes, ao calor axial para cada granulometria e para as diferentes temperaturas do leito.
Tabela 5.2 Valores médios das entalpias das duas correntes, da diferença entre elas e do calor axial em
função de temperatura do leito, dp=107,5 µm
dp(µm)
107,5
TL
(ºC)
400
qag
(W)
qar
(W)
qag-qar
(W)
qaxial
(W)
317
73
244
44
500
396
100
296
89
550
516
113
403
------
600
703
101
602
110
660
915
112
803
188
Tabela 5.3 Valores médios das entalpias das duas correntes, da diferença entre elas e do calor axial em
função de temperatura do leito, dp=142,5 µm
dp(µm)
142,5
TL
(ºC)
qag
(W)
qar
(W)
qag-qar
(W)
qaxial
(W)
400
143
69
74
22
500
202
89
113
20
600
299
117
182
58
700
482
133
349
96
87
5.Transferência de calor na ausência de combustão
Tabela 5.4 Valores médios das entalpias das duas correntes, da diferença entre elas e do calor axial em
função de temperatura do leito, dp=180 µm
dp(µm)
180
TL
(ºC)
400
qag
(W)
qar
(W)
qag-qar
(W)
qaxial
(W)
158
74
84
------
500
203
82
121
64
600
278
97
181
68
700
345
106
239
72
Tabela 5.5 Valores médios das entalpias das duas correntes, da diferença entre elas e do calor axial em
função de temperatura do leito para dp=282,5 µm
dp(µ
µm)
282,5
TL
(ºC)
400
qag
(W)
qar
(W)
qag-qar
(W)
qaxial
(W)
174
83
91
66
500
229
103
126
62
600
277
117
160
81
700
304
129
175
73
Tabela 5.6- Valores médios das entalpias das duas correntes, da diferença entre elas e do calor axial
em função de temperatura do leito, dp=357,5 µm
dp(µm)
357,5
88
TL
(ºC)
qag
(W)
qar
(W)
qag-qar
(W)
qaxial
(W)
400
106
66
40
-------
500
169
90
79
-------
600
232
112
120
-------
700
273
136
137
76
5.Transferência de calor na ausência de combustão
Para todas as granulometrias avaliadas verifica-se que quanto maior for a temperatura do
leito maior é a quantidade de calor recebida pela água, não havendo praticamente alteração na
variação da entalpia da corrente gasosa. No entanto, é para as duas dimensões
correspondentes às partículas mais pequenas, nas mesmas condições de operação, que se nota
um maior aumento do aquecimento da água com o aumento da temperatura do leito, apesar de
não haver grande variação na entalpia da corrente gasosa.
Para poder visualizar melhor estes resultados apresentam-se de seguida os gráficos
correspondentes aos valores médios de qag, ao qag-qar e ao qaxial em função da temperatura do
leito, para as cinco granulometrias.
1000
qag(W)
800
600
400
200
0
350
400
450
500
550
600
650
700
750
TL (ºC)
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 5.19 Valores médios da variação da entalpia da água em função de TL.
1000
qag - qar (W)
800
600
400
200
0
350
400
450
500
550
600
650
700
750
TL (ºC)
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 5.20 Valores médios da diferença entre a variação da entalpia da água e do ar função de TL
89
5.Transferência de calor na ausência de combustão
200
qaxial (W)
150
100
50
0
350
400
450
500
550
600
650
700
750
TL (ºC)
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 5.21 Valores médios do calor axial em função de TL
Na Figura 5.19, mostra-se que há uma grande diferença entre o comportamento das
partículas de dp=107,5 µm e todas as outras. Para uma temperatura do leito de 700 ºC também
se torna mais nítida a diferença de comportamento das várias granulometrias.
Para dp=107,5 µm, a partir da temperatura de 500 ºC verifica-se um aumento acentuado
da transferência de calor para a água. Esse aumento, que não pode ser justificado pelo
aumento da transferência de calor por convecção e por condução a partir do ar, uma vez que a
variação da entalpia da corrente gasosa é muito pequena - ver Tabela 5.2 - será então devido,
a outros fenómenos presentes. Estes fenómenos parecem ser mais evidentes nas partículas
mais pequenas do que em todas as outras, o que pode ser confirmado pelos valores de qag-qar
apresentados na Figura 5.20. Os mecanismos de transferência de calor por radiação, por
convecção e condução das próprias partículas são influenciados pela temperatura do leito,
pelas características das partículas e consequentemente pelas características do escoamento do
próprio leito. Apesar de em todos os ensaios efectuados, com todas as granulometrias, o
regime do leito ser borbulhante, as características desse borbulhamento são como já se
mostrou, diferentes de acordo com o tamanho das partículas e com a temperatura do leito.
Não se fala neste momento da influência do caudal de ar, no borbulhamento do leito, uma vez
que os ensaios que agora estão a ser analisados dizem respeito, como aliás foi referido no
início deste ponto 5.2, a um caudal de ar constante de 1 kg/h.
Se for analisado o rácio v0/vmf (ou número de vmf`s) para os dois tamanhos mais
pequenos de partículas e para a temperatura do leito mais alta, verifica-se que para as mais
90
5.Transferência de calor na ausência de combustão
pequenas se tem v0/vmf = 34 e para as outras se tem v0/vmf = 19. Ora este facto vai ser
fundamental para a intensificação da transferência de calor devido ao espalhamento destas
pequenas partículas. Além disso, a maior taxa de transferência de calor para a água pelas
partículas de menor diâmetro, que está associada ao facto de se trabalhar em condições de
v0/vmf mais elevadas, o que provoca maior projecção e espalhamento de partículas para fora
do leito, explica o facto de não se conseguir aquecer o leito nessas circunstâncias, acima de
660 ºC, para caudais de ar 1 kg/h. O que acontece é que uma grande parte do calor que se
fornece ao leito através da resistência eléctrica é imediatamente dissipado para a água de
arrefecimento devido à projecção destas partículas para fora do leito, levando-as a colidir com
as paredes da superfície de transferência de calor, propiciando assim um bom contacto entre
partículas quentes e paredes frias.
Uma outra constatação, que vem dar ênfase à importância que tem o escoamento
verificado no leito no caso das partículas mais pequenas, na transferência de calor, é o valor
obtido para o calor axial, ver Figura 5.21. Se for analisada a referida figura, verifica-se que
para a maioria dos ensaios o calor axial situa-se numa banda entre 25 a 100 W e isto
corresponde, no caso de um caudal de água de 73 kg/h, a um acréscimo da temperatura da
água de 0,5 a 1 ºC. Esta variação é explicada pelos erros inerentes aos aparelhos de medida,
nomeadamente às oscilações que ocorrem no caudal de água. Como se obteve um único caso
de qaxial =188 W, para as partículas de dp=107,5 µm e para TL = 660 ºC, optou-se por não
afectar os resultados obtidos deste factor.
5.3 Influência do caudal de ar na transferência de calor para a água de arrefecimento
Tendo em atenção os limites físicos da instalação experimental, no que diz respeito à
potência de aquecimento, fez-se um estudo comparativo do comportamento das diversas
granulometrias face ao caudal de ar alimentado à coluna, para as várias temperaturas do leito.
Os ensaios foram feitos para mag = 73 kg/h, procurando fixar a queda de pressão do leito em
cerca de 14 cm de H2O, e a gama de operação para o caudal de ar foi como já se referiu
0,82 < mar(kg/h) < 1,5. Neste caso, como o caudal de água é constante optou-se por apresentar
os resultados em termos de variação de temperatura da água.
Cada uma das figuras que a seguir se apresenta refere-se a um tamanho de partículas,
procurando visualizar a influência do caudal de ar para cada temperatura do leito imposta.
91
5.Transferência de calor na ausência de combustão
16
(Tags-Tage) (ºC)
12
8
4
0
300
350
400
450
500
550
600
650
700
750
TL (ºC)
mar=0,82 kg/h
mar=1 kg/h
mar=1,25 kg/h
Figura 5.22 Variação da temperatura da água em função da temperatura do leito para vários caudais de
ar, dp=107,5 µm
8
(Tags-Tage) (ºC)
6
4
2
0
300
400
500
600
700
800
TL (ºC)
mar=0,82 kg/h
mar=1 kg/h
mar=1,25 kg/h
mar=1,5 kg/h
Figura 5.23 Variação da temperatura da água em função da temperatura do leito para vários caudais de
ar, dp=142,5 µm
92
5.Transferência de calor na ausência de combustão
8
(Tags-Tage) (ºC)
6
4
2
0
300
400
500
600
700
800
TL (ºC)
mar=0,82 kg/h
mar=1 kg/h
mar=1,25 kg/h
mar=1,5 kg/h
Figura 5.24 Variação da temperatura da água em função da temperatura do leito para vários caudais de
ar, no caso de dp=180 µm
8
(Tags-Tage) (ºC)
6
4
2
0
300
400
500
600
700
800
TL (ºC)
mar=0,82 kg/h
mar=1 kg/h
mar= 1,25 kg/h
mar=1,5 kg/h
Figura 5.25 Variação da temperatura da água em função da temperatura do leito para vários caudais de
ar, no caso de dp=282,5 µm
93
5.Transferência de calor na ausência de combustão
8
(Tags-Tage) (ºC)
6
4
2
0
300
400
500
600
700
800
TL (ºC)
mar=0.82 kg/h
mar=1 kg/h
mar=1,25
Mar=1,5
Figura 5.26 Variação da temperatura da água em função da temperatura do leito para vários caudais de
ar, no caso de dp=357,5 µm
Uma das conclusões que se pode tirar imediatamente de uma primeira análise destas
figuras é que seja qual for a temperatura do leito, e seja qual for a granulometria, a variação
da temperatura da água é tanto maior quanto maior for o caudal de ar. Isto é de esperar, uma
vez que ao aumentar o caudal de ar aumenta-se a transferência de calor por convecção, assim
como, a projecção de partículas para fora do leito que chocarão posteriormente com a
superfície de transferência de calor.
No entanto verifica-se que à medida que a temperatura do leito aumenta podem ocorrer
duas situações:
- ∆Tag obtido acentua-se para os dois grupos de partículas mais pequenas: dp=107,5 µm e
dp=142,5 µm.
- ∆Tag obtido, aumenta praticamente da mesma maneira para as outras granulometrias,
mas este aumento não é tão acentuado como para as duas menores granulometrias.
Estas ocorrências estão relacionadas com a transferência de calor por parte do próprio
leito, sendo mais evidentes quando ele é formado pelas partículas mais pequenas, devido ao
borbulhamento mais intenso que aí se atinge. Esta situação, torna-se ainda mais importante
quando a temperatura do leito aumenta. Portanto, a temperatura que o leito atinge é uma
condição necessária para aumentar a taxa de transferência de calor tanto por
convecção/condução como por radiação, mas são os fenómenos associados ao movimento de
94
5.Transferência de calor na ausência de combustão
projecção das partículas para fora do leito, que parecem ser os factores mais importantes no
que diz respeito ao aumento da taxa de transferência de calor, para a água de arrefecimento.
Tudo isto também justifica de algum modo o facto de não se conseguir trabalhar com
todos os caudais de ar e em toda a gama de temperatura para todas as granulometrias
estudadas. Para as partículas mais pequenas, e de acordo com o que já foi referido e
referenciado na Tabela 5.1, é natural que não se consigam atingir aí as temperaturas mais
elevadas, pois, o calor que lhe é fornecido pela resistência de aquecimento é rapidamente
transportado para a água, devido ao movimento mais intenso das partículas.
Deste modo, e em jeito de conclusão pode-se dizer que são todos os valores
experimentais obtidos, para todas as temperaturas do leito impostas, para todos os caudais de
água, para todos os caudais de ar e para todos os tamanhos de partículas, cujos valores médios
correspondentes a cada ensaio, estão apresentados no Apêndice V, que vão ser usados para se
determinar um coeficiente global de transferência de calor do leito. Assim, é possível
determinar correlações empíricas, expressas em termos de grupos adimensionais
caracterizadores das condições físicas a que o leito opera, que permitam quantificar esse
mesmo coeficiente em função do correspondente número de Nusselt.
Face ao que foi exposto, pode-se concluir que este coeficiente global de transferência de
calor que se pretende determinar, engloba os seguintes mecanismos:
- Transferência de calor por convecção/condução do ar para a parede interior do
permutador;
- Transferência de calor por radiação directamente do leito para a parede interna do
permutador;
- Transferência de calor devido ao movimento das partículas no leito.
95
5.Transferência de calor na ausência de combustão
5.4 Desenvolvimento de uma correlação empírica para determinação do coeficiente
global de transferência de calor do leito - hglo
Pretende-se fazer este desenvolvimento em termos de grupos adimensionais apropriados
que possam influenciar o valor do coeficiente global de transferência de calor do leito. O uso
de grupos adimensionais, além de permitir a obtenção de relações mais simples entre as
variáveis que se pretendem relacionar, permite também definir limites de aplicação mais
generalizados para a função encontrada.
A escolha das grandezas físicas deve ter como base um conhecimento prévio da
natureza do fenómeno que se está a estudar, e que neste caso concreto é a transferência de
calor de um leito de partículas de areia para a superfície de um permutador de parede
membrana. Se uma variável incluída na função, não exercer uma grande influência no
problema, o grupo adimensional onde ela aparece terá um efeito reduzido na solução
numérica do problema, e o expoente desse grupo será próximo de zero. Por outro lado, se for
esquecida alguma variável importante, não será possível encontrar uma relação única entre os
grupos adimensionais.
Neste caso concreto, e tendo um conhecimento prévio dos fenómenos de transferência
de calor, alguns grupos adimensionais conhecidos farão com certeza parte da correlação
empírica a determinar, são eles:
- Número de Nusselt – Nu;
- Número de Reynolds – Re;
- Número de Prandtl – Pr;
No entanto, face às várias grandezas físicas envolvidas, nomeadamente o tamanho das
partículas, o diâmetro da coluna, o regime de fluidização do leito, a temperatura do leito do
gás e da parede, vai haver necessidade de introduzir na correlação procurada, outros grupos
adimensionais. Além disso, é preciso definir qual a dimensão característica a usar no número
de Reynolds e no número de Nusselt e ainda a temperatura mais correcta para o cálculo das
propriedades do fluido.
Face ao que se acaba de expor é conveniente recorrer ao teorema Pi de Buckingham
para tentar encontrar de uma maneira mais fundamentada a correlação adimensional
procurada.
96
5.Transferência de calor na ausência de combustão
5.4.1 Teorema Pi de Buckingham- fundamentos teóricos
Este teorema começa por estabelecer que o número de grupos adimensionais que entra
na função procurada, é igual ao número de variáveis menos o número de grandezas
fundamentais. No entanto, e segundo Coulson (1965), nos casos em que duas grandezas
fundamentais apareçam sempre na mesma combinação – por exemplo, comprimento e tempo
sempre em LT-1 – elas corresponderão a uma única grandeza fundamental em vez de duas, e
este facto leva a que o número de grupos adimensionais seja maior do que o estabelecido por
este teorema.
A função que se procura pretende ser uma relação funcional entre as várias variáveis
intervenientes no fenómeno em estudo, e pode ser escrita do seguinte modo:
f1 (hglo, ρg, µg, cpg, kg, Tgs, TL, Tw, v0, vmf, dp, di ) = 0
(5.3)
nesta expressão não se faz referência às propriedades físicas da areia nomeadamente, massa
volúmica, ρp, e capacidade calorífica, cs. A massa volúmica, embora seja determinada
experimentalmente é praticamente constante para as diferentes granulometrias e considera-se
constante com a temperatura. A capacidade calorífica da areia como de qualquer material, é
uma indicação da capacidade que esse material tem para absorver energia, ficando mais ou
menos energia disponível para ser transportada. Deste modo, o valor desta grandeza tem
influência na quantidade de calor transferida para a água, contudo não se inclui na relação
acima referida, porque é também um valor constante. Ainda se poderia pensar em incluí-la de
uma maneira adimensional, tendo em atenção a capacidade calorífica do ar , ou seja na forma
de: cs /cpg. Também se optou por não o fazer pois a capacidade calorífica do ar é também um
valor praticamente constante com a temperatura. Este grupo, apenas tornaria a correlação
mais pesada e poderia acarretar problemas numéricos na convergência. Voltando novamente à
equação anterior, 5.3, esta pode ser escrita de uma maneira mais genérica, não sendo
necessário explicitar as várias temperaturas no interior do permutador, desde que elas entrem
todas num grupo adimensional que irá fazer parte da correlação. Sendo assim pode-se
escrever novamente:
f2 (hglo, ρg, µg, cpg, kg, Tin, v0, vmf, dp, di ) = 0
(5.4)
97
5.Transferência de calor na ausência de combustão
em que a variável Tin engloba as temperaturas no interior do permutador que têm influência
no processo de transferência de calor
As grandezas fundamentais são M, L, T e K, o que significa que estando na função f2
definidas 10 variáveis, então a correlação procurada deverá constar de 6 grupos
adimensionais. Para definir esses grupos é conveniente escolher 4 variáveis das 10
mencionadas em f2, tendo o cuidado de as escolher de tal maneira, que cada uma das
grandezas fundamentais entre pelo menos numa das variáveis escolhidas, e não seja possível
formar com algumas delas, ou com todas, um grupo adimensional.
As variáveis escolhidas foram:
Tabela 5.7. Variáveis escolhidas para a análise dimensional
Variáveis
Dimensões
di
L
kg
M L T-3 K-1
ρg
M L-3
vmf
LT-1
Deve-se agora igualar cada variável à dimensão correspondente e resolver as equações
obtidas em ordem às grandezas fundamentais. O resultado obtido foi o seguinte:
L=di
M= ρg di3
T= di v0-1
K= ρg di v03/ kg
Falta agora considerar as variáveis que não foram escolhidas, e de acordo com as suas
dimensões e com as equações obtidas para as grandezas fundamentais, transformá-las em
grupos adimensionais. O resultado obtido foi:
- hglo[MT-3K-1] x ( M-1T3K) = hglo di/ kg = Nu
(5.5)
- µg [ML-1T-1] x ( M-1LT) = µg/(ρg v0 di) = 1/ Rear
(5.6)
- cpg [L2T-2K-1] x ( L-2T2K) = cpg v0 ρg di/ kg
(5.7)
-1
98
-1
- v0 [LT ] x (L T) = vmf / v0
(5.8)
- di [L] x L-1 = di/dp
(5.9)
5.Transferência de calor na ausência de combustão
Falta ainda formar o grupo adimensional correspondente a todas as temperaturas envolvidas
no interior do permutador, e que se encontra representado na função f2 por Tin. Optou-se por
considerar o seguinte grupo adimensional:
ln((TL-Tw)/(TL-Tgscorr))
(5.10)
Este grupo, que corresponde a uma variação de temperatura adimensional, envolve de algum
modo, o gradiente térmico para a radiação e a variação da temperatura do ar que está
relacionada com a transferência de calor por convecção forçada.
Há ainda um ajuste que se pode fazer tendo em conta o resultado obtido na equação 5.7.
Se se multiplicar e dividir o 2º membro dessa equação por µg obtém-se o seguinte:
cpg v0 ρg di/ kg = (cpgµg/ kg)( v0 ρg di /µg) = Pr. Rear
(5.11)
Apesar desta equação 5.11 conduzir a um grupo adimensional, dado como o produto de Pr e
Rear, para efeitos da correlação procurada só interessa considerar o número de Prandtl, uma
vez que o número de Reynolds do ar aparece já definido na equação 5.6.
Como conclusão a correlação que se procura poderá ser dada pela seguinte função:

 T − Tw
v dp
f 3  Nu , Re ar , Pr, 0 , , ln  L corr
 T −T

vmf d i
 L gs


  = 0


(5.12)
ou seja,

 T − Tw
v dp
Nu = f 4  Re ar , Pr, 0 , , ln  L corr
 TL − Tgs

vmf d i



 


(5.13)
É esta função f4, que vai ser escolhida para tentar obter uma correlação empírica que
permita o cálculo do coeficiente global de transferência num leito fluidizado borbulhante, no
caso concreto de ausência de combustão.
99
5.Transferência de calor na ausência de combustão
5.4.2 Correlação empírica obtida
De acordo com o que já foi referido, os dados experimentais que vão ser usados para a
procura da correlação empírica adequada, são os correspondentes a todos os ensaios feitos
para as cinco granulometrias de areia usada. Cada ensaio, para cada granulometria, diz
respeito a uma dada temperatura do leito, a um caudal de ar e a um caudal de água. Para cada
um deles eles, calcula-se o calor transferido para a água de arrefecimento em cada instante, à
custa das temperaturas de entrada e saída da água e faz-se então, a média desse calor face à
duração do ensaio. A partir desse valor é feito o cálculo de hgloexp que é baseado em ∆TlnL-w
definido como:
∆Tln L−w =
(TL − T corr gs )
 T −T 
ln  corrL w 
 T gs − Tw 


(5.14)
e na área interna do permutador. O valor obtido de hgloexp é então adimensionalizado obtendose o valor do número de Nusselt, Nuexp.
Optou-se por não considerar nesta fase, a temperatura do gás à entrada Tgecorr, pois o
coeficiente global de transferência de calor pretende quantificar o calor total transferido para a
água de arrefecimento, considerando como sistema de aquecimento o conjunto formado pelo
leito e permutador de calor. Os mecanismos envolvidos nesta troca de calor, e que têm de ser
contabilizados neste mesmo coeficiente, correspondem à convecção do ar, à convecção e
condução pela parte das partículas e à radiação. Assim, parece ser mais adequado escolher
como temperatura inicial para a transferência de calor o próprio leito.
Uma das outras escolhas que é necessário fazer antes de passar à fase de verificação da
correlação proposta é a escolha da dimensão característica a usar quer em Nuexp quer em Rear.
As duas opções referem-se ao diâmetro da partícula ou ao diâmetro interior do leito. Foi
considerada a última, ou seja o diâmetro interior do leito, pois o regime de escoamento no
leito nas condições de operação não passou de borbulhante e portanto não houve circulação
significativa de sólidos. Deste modo, a zona de transferência de calor diz respeito a toda uma
coluna de diâmetro interior di.
Por último, é preciso ainda definir a temperatura para a qual se determinam as
propriedades do ar. Mais uma vez, tendo em atenção que se estão a estudar os fenómenos de
100
5.Transferência de calor na ausência de combustão
convecção e de radiação para a parede do permutador, as temperaturas em jogo são, TL, Tw e
Tgscorr. Faz-se então a determinação da temperatura de filme Tf, sendo dada pela expressão:
Tf
( (T
=
L
)
+ T corr gs ÷ 2 + Tw
)
(5.15)
2
Todos os dados experimentais bem como os resultados obtidos para a determinação da
correlação empírica procurada são apresentados no Apêndice V.
Estando então tudo definido, os valores obtidos para Nuexp são ajustados por uma
expressão do tipo,
Nuexp
 v
= a Reb Pr  0
 vmf

c
d
  d p    TL − Tw
    ln 
corr

  di    TL − Tgs

 


e
(5.16)
Esta expressão envolve 5 parâmetros – a, b, c, d, e – que são determinados através de
um programa que envolve um método de optimização – Programa de Análise de regressão
não linear, NLREG.
Depois de se conhecerem os parâmetros envolvidos, calculam-se então para as
condições experimentais os valores de Nucal. e comparam-se os valores obtidos com os valores
correspondentes de Nuexp.
A correlação empírica encontrada que permite determinar os valores de Nucalc é a
seguinte:
Nucalc = 14, 7 Re
−0,35
 v
Pr  0
 vmf




−0,09
 dp 
 
 di 
−0,47
  T −T
w
 ln  L corr
  TL − Tgs
 

 


0,21
(5.17)
esta correlação é válida para a areia fluidizada com ar à pressão atmosférica, numa coluna de
diâmetro interno 0,0545 m e dentro dos seguintes limites:
101
5.Transferência de calor na ausência de combustão
- 107,5 < dp (µm) < 357,5
- 400 < TL (ºC) < 700
- 200 < Rear < 400
- 2 < v0/vmf < 40
O resultado obtido pode ser visualizado na figura seguinte:
30
25
Nuexp
20
15
10
pontos experimentais
linha de ajuste
5
y = 0.985x + 0.475
0
0
5
10
dp=107,5
Nucalc
dp=142,5
dp=180
15
20
dp=282,5
25
dp=357,5
Figura 5.27 Valores de Nuexp, e ajuste linear de Nucal versus Nuexp, 99 observações
Nesta Figura 5.27 apresenta-se a equação da linha de ajuste entre pontos calculados e
experimentais, pois é necessário o conhecimento prévio do declive e da ordenada na origem
para poder fazer a análise estatística da correlação encontrada, que vem referida na secção
5.4.3.
Foi determinado o valor do desvio médio calculado a partir da expressão proposta por
Wen and Chen (1982):
 Nu calc ,i − Nuexp,i
Dm (%) = ∑ 

Nuexp,i
i =1 
n
2

 ÷ n × 100

(5.18)
sendo n o número de observações experimentais que neste caso foi de 99. O valor obtido para
o desvio médio foi de:
102
5.Transferência de calor na ausência de combustão
Dm =18%
Apesar de se ter obtido um ajuste relativamente fraco, o valor de um desvio médio de
18% é bastante bom, se atendermos ao facto de que na maioria das correlações empíricas
apresentadas em bibliografia o desvio é em geral acima de 30%.
O programa de optimização NLREG, além de permitir o cálculo dos parâmetros
envolvidos na correlação procurada, também permite uma primeira análise estatística no que
diz respeito à importância relativa de cada um dos parâmetros envolvidos. Deste modo, este
programa calcula o valor de uma variável designada por Prob(t) que se refere à probabilidade
do parâmetro estimado ser zero. Se essa probabilidade for grande, ou seja próximo de 1,
significa que a variável a que o parâmetro diz respeito pouca importância tem na correlação
final. Apresenta-se de seguida, a tabela dos valores obtidos de Prob(t) para cada um dos 5
parâmetros introduzidos na correlação 5.17
Tabela 5.8 Estimativas finais dos parâmetros da correlação 5.17 e sua importância relativa- método de
optimização “NLREG”
Parâmetro
Variável
a
Parâmetro
Prob(t)
14,7
0,36
b
Re
-0,35
0,03
c
v0/vmf
-0,09
0,24
d
dp/di
-0,47
6x10-4
0,21
1x10-5
e
ln((TL-Tw)/(TLTgs
corr
))
Embora com importâncias relativas de diferentes ordens de grandeza, todas as variáveis
envolvidas na correlação 5.17 são importantes na correlação determinada.
Também se pode analisar graficamente a dispersão dos pontos relativamente à bissectriz
do 1º quadrante. Se for traçada essa bissectriz e a partir dela duas rectas que passem na
origem dos eixos e que tenham um desvio relativamente a ela de ± 25% o resultado é o
seguinte:
103
5.Transferência de calor na ausência de combustão
25
20
25%
Nuexp
15
-25%
10
5
0
0
5
10
15
20
25
Nucalc
Figura 5.28 Desvio de ±25% da correlação 5.17, relativamente à recta y = x
5.4.3 Análise estatística da correlação encontrada
O desvio médio de 18% na correlação empírica encontrada e definida no ponto anterior,
é por si só uma medida de confiança. No entanto, Vardeman (1994) define um método, que
permite determinar em simultâneo intervalos de confiança dos dois lados da recta de ajuste
dos pontos experimentais e calculados. De acordo com este método, se os limites de confiança
encontrados englobarem a bissectriz do 1º quadrante, y = x, pode-se considerar que há uma
evidência estatística entre os valores observados e os valores calculados. Este teste é mais
abrangente que o teste de hipóteses de t de Student, que obriga a uma simultaneidade de
confiança na ordenada na origem e no declive, para que se possa concluir da evidência
estatística entre valores experimentais e calculados.
Apresenta-se na figura seguinte o resultado do método proposto por Vardeman (1994).
Como se pode verificar os limites traçados com uma confiança de 95%, englobam a bissectriz
do 1º quadrante. Este facto permite aceitar com esse nível de confiança, a correlação
encontrada.
104
5.Transferência de calor na ausência de combustão
25
20
Nuexp
15
10
5
0
0
5
10
15
20
25
Nucalc
Figura 5.29. Recta de ajuste e limites de 95% de confiança para a correlação empírica 5.17
Também neste caso se verifica o teste de hipóteses de t de Student. Este teste diz que só
é possivel aceitar com segurança o ajuste obtido entre pontos experimentais e calculados se
t(A) e t(B), forem ambos inferiores ao valor de t (Student). Este último é visto na tabela de
distribuição de Student para um nível de confiança de 95% e (n-2) graus de liberdade, sendo n
o número de observações experimentais. Neste caso concreto obteve-se,
- Para 97 graus de liberdade e 95% de confiança t = 1,67;
- t(A) = 0,45;
- t(B) = 0,18.
5.5 Análise de tendências no valor de Nuexp
Como já se pôde constatar no ponto 5.2 deste capítulo, nomeadamente na Figura 5.19,
as partículas mais pequenas são as mais eficientes no que diz respeito à taxa de transferência
de calor para a água. Para qualquer granulometria estudada, essa quantidade de calor aumenta
com o aumento da temperatura do leito e com o aumento do caudal de ar, embora seja com as
partículas mais pequenas que esse aumento é mais notório. Por outro lado, o aumento da
temperatura do leito pouco altera a variação da entalpia da corrente de ar. Isto leva a concluir
que embora a convecção forçada, devido ao movimento ascendente da corrente de ar, tenha
influência na transferência de calor, são as características do regime de escoamento do próprio
leito que vão interferir mais na taxa de transferência de calor. Como já se disse, para as
mesmas condições de operação, o quociente v0/vmf que se atinge para as partículas mais
105
5.Transferência de calor na ausência de combustão
pequenas é muito superior ao que se atinge para as outras granulometrias. Este facto, aliado à
constatação da maior taxa de transferência de calor por parte destas partículas, permite
concluir que não só é o fenómeno de radiação que se torna mais evidente para temperaturas
do leito superiores a 500ºC, mas também, que o alto valor do quociente v0/vmf, será um
indicador do aumento da taxa de transferência de calor, pois está associado à projecção de
partículas para fora do leito até à zona do permutador.
Para melhor se entender o que se acaba de dizer é importante analisar os dados
experimentais no que diz respeito à variação de Nuexp versus TL e versus v0/vmf .
25
Nuexp
20
15
10
5
0
300
400
500
600
700
800
TL (ºC)
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 5.30 Variação de Nuexp versus TL para todas as condições de operação sem combustão.
Como se pode verificar destacam-se as partículas de dp=107,5 µm, com Nusselt
essencialmente acima de 20. Para os outros tamanhos, o valor de Nuexp situa-se na maioria dos
casos na gama entre 10 a 15.
Se for analisada a isotérmica correspondente a 550ºC, para dp=107,5 µm verifica-se um
grande aumento de Nuexp que corresponde a um aumento do caudal de ar e portanto a um
aumento da taxa de transferência de calor por convecção. No entanto, este aumento do caudal
de ar traduz-se também num aumento de v0/vmf que leva a um maior afastamento entre as
partículas que constituem o leito. É este regime de escoamento do leito que vai acentuar, no
caso destas partículas, o aumento de Nuexp. Esta variação de Nuexp é ainda de alguma maneira
notória para as partículas de dp=142,5 µm, mas passa a ser pouco ou nada evidente para todos
106
5.Transferência de calor na ausência de combustão
os outros tamanhos. Nesses casos, quer aumente a temperatura do leito, quer aumente o
caudal de ar, o valor de Nuexp pouca variação sofre.
A influência de v0/vmf nos valores de Nuexp e consequentemente na taxa de calor
transferida para a água, pode também ser visualizada na Figura 5.31,
25
20
Nuexp
15
10
5
0
0
5
10
dp=107
15
dp=142.5
20
v0/vmf
dp=180
25
30
dp=282.5
35
40
dp=357.5
Figura 5.31 Variação de Nuexp versus v0/vmf para todas as condições de operação sem combustão.
Para as mesmas condições de operação, é para as partículas de dp=107,5 µm, que se
atingem os maiores valores v0/vmf . É este facto que leva à obtenção valores mais altos de
Nuexp.
Para as partículas de dp=142,5 µm, as condições de operação conduzem a v0/vmf entre 10
e 20 o que leva ainda a um aumento notório nos valores de Nuexp com o aumento de v0/vmf.
Para dp=180 µm, embora se consigam atingir valores de v0/vmf da ordem de 25, porque
neste caso se consegue trabalhar com maiores caudais de ar às temperaturas mais altas, ver
Tabela 5.1, isso pouca infuência tem no valor de Nuexp. Isto significa, que apesar do leito
destas partículas atingir um tipo de escoamento muito semelhante ao conseguido com as de
dp=142,5 µm, o aumento da convecção devido ao aumento do caudal de ar, e o aumento da
radiação devido à temperatura do leito e às suas características, não se traduz num aumento
efectivo da taxa de transferência de calor para a água. As outras duas dimensões apresentam
um comportamento muito semelhante, e, apesar de se trabalhar numa gama de v0/vmf muito
mais baixa os valores de Nuexp são da mesma ordem de grandeza dos obtidos para dp=180 µm.
107
5.Transferência de calor na ausência de combustão
Como conclusão final da análise deste gráfico pode dizer-se o seguinte:
- há um aumento Nuexp quando o diâmetro das partículas diminui;
- há dois comportamentos distintos: as partículas correspondentes a dp=107,5 µm e a
dp=142,5 µm têm um comportamento semelhante; as partículas correspondentes a
dp=282,5 µm e a dp=357,5 µm têm também entre si um comportamento semelhante
mas diferente das anteriores;
- as partículas de dp=180 µm devem constituir uma dimensão crítica, tendo em atenção o
diâmetro da coluna onde estão inseridas. Pela análise feita verifica-se que apresentam
um comportamento semelhante às anteriores no que diz respeito à transferência de
calor, mas em termos de condições de escoamento no leito assemelham-se às de
dp=142,5 µm.
Por último, pode-se ainda analisar a variação de Nuexp com ∆TlnL-w, já que foi com base
neste gradiente de temperatura, que se procedeu ao cálculo do coeficiente global de
transferência de calor do leito, e consequentemente, de Nuexp.
25
20
Nuexp
15
10
5
0
0
100
dp=107,5
200
dp=142,5
∆TlnL-W
dp=180
300
dp=282,5
400
500
dp=357,5
Figura 5.32. Variação de Nuexp versus ∆TlnL-w para todas as condições de operação sem combustão.
Através deste gráfico pode-se também constatar, que para as três maiores dimensões de
partículas o valor de Nuexp pouco é influenciado pelo gradiente térmico, enquanto que para os
dois tamanhos mais pequenos há uma tendência para um aumento de Nuexp com ∆TlnL-w.
108
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
6.Considerações sobre o comportamento das partículas
relativamente ao calor transferido
6.1 Análise dos resultados experimentais de hglo para cada granulometria - comparação
de resultados.
É importante analisar o comportamento individual da cada granulometria, face à
transferência de calor que ocorre para a parede interna do permutador. Como se pode
constatar pelas Tabelas 5.2 a 5.6, apresentadas no Capítulo 5, e pela Figura 5.19, são as
partículas de dp = 107,5 µm que se destacam de todas as outras, devido à maior taxa de
transferência de calor para a água de arrefecimento. Para as mesmas condições de operação a
grande diferença que ocorre, quando se usam diferentes granulometrias, reside nas
características de escoamento do leito de partículas. É para as partículas de menor dimensão
que o leito atinge um maior grau de borbulhamento, sendo esta a causa que justifica a maior
quantidade de calor transferida. Para estas, há maior excesso de gás que sobe através do leito
sob a forma de bolhas e provoca a projecção das partículas contra a parede do permutador.
Além disso, também o fenómeno de radiação que será mais evidente a partir de TL>500ºC,
pode ser intensificado pelo grau de borbulhamento do leito. São também estas características
do leito, que não permitem a obtenção de uma temperatura de funcionamento de 700 ºC
quando se pretende trabalhar com caudais de ar iguais ou superiores a 1 kg/h. Para
temperaturas elevadas, e numa fase preparatória de acerto da temperatura do leito, à medida
que se fornecia calor ao leito, este passava rapidamente para a água através das paredes do
permutador sem se conseguir atingir no leito estado estacionário. Este comportamento que é
acentuado para partículas de 107,5 µm, ainda se nota de alguma forma nas partículas de
109
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
142,5 µm, contudo para as partículas de maiores dimensões deixa de ser importante. Além
disto, e para caudais de ar de 1 kg/h, - ver Tabelas. 5.2 a 5.6-, também se pode constatar que o
aumento da temperatura do leito pouca influência tem no aumento da entalpia do ar, o que
mais uma vez reforça a ideia de que é a projecção de partículas para fora do leito e contra as
paredes do permutador o fenómeno mais importante.
Para poder visualizar as diferenças de comportamento das diversas granulometrias
apresentam-se de seguida as figuras de hgloexp em função de ∆TlnL-w. Todas estas figuras dizem
respeito a todas as condições de operação, de temperatura imposta no leito e caudal de ar
20
hgloexp (W/m 2ºC)
16
12
8
4
0
0
100
200
300
400
500
∆TlnL-w
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 6.1 Valores do coeficiente global de transferência de calor hgloexp versus ∆TlnL-w
Nesta Figura 6.1 mostra-se que existe uma diferença nítida entre as partículas de menor
dimensão e todas as outras. No entanto, também de pode verificar que as partículas
correspondentes a dp=142,5 µm se destacam das outras três granulometrias maiores sobretudo
para valores de ∆TlnL-w superiores a 300 ºC.
Deste modo, e para melhor se poder distinguir os diferentes comportamentos, optou-se
por apresentar mais duas figuras. Numa primeira, apresentam-se os valores de hgloexp obtidos
para as duas granulometrias mais pequenas e numa outra apresentam-se os mesmos valores
experimentais mas para as três granulometrias maiores.
110
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
20
hglo exp(W/m2ºC)
16
12
8
4
0
0
100
200
300
400
500
∆TlnL-w
dp=107,5
dp=142.5
Figura 6.2 Valores do coeficiente global de transferência de calor hgloexp versus ∆TlnL-w , dp = 107,5 µm
e dp = 142,5 µm
12
hgloexp (W/m2ºC)
9
6
3
0
0
100
200
dp=180
∆TlnL-w
300
dp=282,5
400
500
dp=357,5
Figura 6.3 Valores do coeficiente global de transferência de calor hgloexp versus ∆TlnL-w , dp = 180 µm;
dp = 282,5 µm e dp = 357,5 µm
Na Figura 6.2 é evidente a tendência para um aumento de hgloexp com o aumento de
∆TlnL-w. Para o mesmo valor ∆TlnL-w, hgloexp é maior para as partículas mais pequenas, sendo
esta diferença acentuada à medida que ∆TlnL-w aumenta.
Pela análise da Figura 6.3 o que se pode constatar é que a variação de hgloexp com ∆TlnL-wpara qualquer um destes três tamanhos maiores, é muito menos evidente. Para ∆TlnL-w < 200,
111
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
nota-se uma diferença, embora pequena, nos valores de hgloexp. São as partículas
correspondentes a dp=357,5 µm, que apresentam valores mais baixos, as de dp=282,5 µm
apresentam valores mais altos, e por fim as partículas de dp=180 µm permitiram obter valores
intermédios. Seria de esperar, que fossem as partículas de dp=180 µm que conduzissem a
valores de hgloexp mais altos devido ao maior grau de borbulhamento, no entanto, como já se
referiu, este tamanho parece ser um tamanho crítico face ao diâmetro do leito. Embora o seu
comportamento em termos da hidrodinâmica do leito seja semelhante ao das partículas de
dp=142,5 µm, em termos transferência de calor o seu comportamento assemelha-se às duas
dimensões maiores de partículas. Para valores de ∆TlnL-w superiores a 300ºC as partículas
apresentam todas o mesmo comportamento e os valores de hgloexp são praticamente constantes
e iguais a 7 W/m2ºC.
Face a estes resultados, tentou-se determinar duas correlações empíricas, uma para cada
conjunto de tamanhos, em termos dos mesmos grupos adimensionais referidos no Capítulo 5.
6.1.1 Correlações empíricas obtidas para os dois menores tamanhos e para os três
maiores
Pretendeu-se, a título de comparação, envolver nas correlações procuradas as mesmas
variáveis que se usaram no Capítulo 5. As correlações obtidas para os dois grupos de
tamanhos referidos permitiram obter desvios médios mais baixos do que o obtido pela
correlação 5.17, o que aliás seria de esperar.
Para o grupo de partículas correspondente às três maiores dimensões verificou-se que o
termo adimensional das temperaturas, em nada modificava o resultado obtido em termos do
ajuste encontrado, por isso, não tem qualquer interesse a sua introdução na correlação
procurada.
De acordo com o programa de análise de regressão não linear, NLREG, a correlação
obtida para as duas menores dimensões foi a seguinte:
Para dp=107,5 µm e dp=142,5 µm:
Nucalc
112
 v
= 0, 058 Re0,24 Pr  0
 vmf




0,38
 dp 
 
 di 
−0,58
  T −T
 ln  L w
  TL − Tgs
 

 


0,13
(6.1)
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
A figura que se segue permite uma comparação entre os valores experimentais e calculados
para o número de Nusselt. Para tornar essa comparação mais evidente é marcada também na figura
a recta y = x.
25
Nucalc
20
15
10
5
0
0
5
10 Nuexp
dp=107,5
15
20
25
dp=142,5
Figura 6.4 Nucalc versus Nuexp para as partículas de dp=107,5 µm e dp=142,5µm e 42 observações
Neste caso o desvio médio obtido foi de Dm = 12%
Para dp=180 µm, dp=282,5 µm e dp=357,5 µm, já sem o termo de ln((TL-Tw)/(TL-Tgs corr), o resultado
foi seguinte,
Nucalc = 0,38 Re
0,22
 v
Pr  0
 vmf




−0,18
 dp 
 
 di 
−0,51
(6.2)
Segue-se também a Figura 6.5 que pretende comparar os valores do número de Nusselt
experimentais com os obtidos pela correlação 6.2,
113
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
15
12
Nucalc
9
6
3
0
0
3
6
dp=180
Nuexp
dp=282,5
9
12
15
dp=357,5
Figura 6.5 Nucalc versus Nuexp para as partículas de dp=180 µm, dp=282,5 µm e dp=357,5 µm, e 57
observações
Neste caso o desvio médio obtido foi de Dm = 10 %
Apresenta-se de seguida a Figura 6.6 onde se mostram todos os valores do número de
Nusselt experimental para todas as partículas e os correspondentes valores calculados pela
equação (6.1) no caso das duas menores dimensões, e os calculados pela equação (6.2) no
caso das três maiores dimensões
25
20
Nucalc
20%
15
-20%
10
5
0
0
5
10
Nuexp
equação 6.1
15
20
25
equação 6.2
Figura 6.6 Nucalc pelas equações 6.1 e 6.2 versus Nuexp para todas as partículas e 99 observações.
Neste caso o desvio médio obtido foi apenas de Dm=11%.
114
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
Em resumo, as equações 6.1 e 6.2 permitem reduzir o desvio médio comparativamente
aos resultados que se obtiveram com a equação 5.17, se bem que todos os desvios sejam da
mesma ordem de grandeza.
6.2 Efeito da projecção de partículas na transferência de calor.
De acordo com o que foi dito no ponto 6.1, pretende-se agora fazer um estudo das
variáveis que podem de algum modo quantificar a projecção de partículas da superfície do
leito para a parede do permutador, devido às bolhas que rebentam à superfície. Claro que o
fluxo de partículas projectadas está relacionado com o grau de borbulhamento do leito e por
isso com o parâmetro v0/vmf, já introduzido nas correlações apresentadas. No entanto, vai-se
aqui procurar outras variáveis que possam estar mais directamente ligados ao fluxo de
partículas projectadas e verificar de que maneira elas podem alterar, no sentido de uma
melhoria ou não, a correlação 5.17 apresentada no Capítulo 5. Sendo assim, uma outra
alteração que deve ser aqui estudada e que está ligada a essas novas variáveis que se
procuram, é sem dúvida a temperatura à qual é feito o cálculo das propriedades do ar. Se a
transferência de calor que ocorre para a água é essencialmente devido ao maior fluxo de
partículas projectadas e por isso também a um possível incremento na radiação, fenómenos
estes que são mais evidentes para as partículas mais pequenas, então as temperaturas mais
influentes nestes processos serão: a temperatura do leito e a temperatura da parede. Optou-se
então nesta fase, por calcular as propriedades do ar à temperatura média entre leito e parede
TmL-w. = (TL+Tw)/2
6.2.1 Excesso de gás
Uma das variáveis, que está relacionada com o fluxo de partículas a partir da superfície
do leito é sem dúvida o excesso de gás que passa pelo leito sob a forma de bolhas. Deste
modo, alterou-se a correlação 5.17 obtida no Capítulo 5, e em vez do grupo v0/vmf introduziuse o grupo v0/(v0-vmf), e calcularam-se as propriedades do ar à TmL-w
A correlação empírica encontrada e que permite calcular os valores de Nucalc é a
seguinte:
115
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
Nucalc
 v0
= 0, 77 Re −0,13 Pr 

 v0 − vmf



0,78
 dp 
 
 di 
−0,69
  T −T
w
 ln  L corr
  TL − Tgs
 

 


0,24
(6.3)
A figura que se segue mostra, os pontos experimentais, e a proximidade entre valores
experimentais e calculados relativamente à recta y=x
25
Nucalc
20
15
10
5
0
0
5
10
15
20
25
Nuexp
Figura 6.7 Nucalc pela equação 6.3 versus Nuexp , e 99 observações
O valor obtido para o desvio médio foi de: Dm =19%.
Ora este desvio não é melhor do que o obtido pela correlação 5.17, o que significa que
relativamente à fluidização incipiente, o emprego de um factor de excesso de ar v0/(v0-vmf) não
apresenta grande melhoria em relação a v0/vmf
6.2.2 TDH
Um das variáveis empíricas que está relacionada com a quantidade de partículas
projectadas é sem dúvida o valor de TDH -“altura de desagregação” Este valor que é uma
variável de projecto, é a altura medida a partir da superfície do leito a partir da qual a taxa de
elutriação de sólidos é constante. Num leito fluidizado circulante, a saída do gás deve situarse acima deste valor. Apesar de não se terem atingido as condições de operação necessárias à
circulação de sólidos, a projecção de partículas que ocorre está sem dúvida relacionada com o
116
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
valor de TDH, na medida em que quanto maior for o excesso de gás sob a forma de bolhas,
maior será a quantidade de partículas transportadas pelo gás e maior terá de ser então o valor
de TDH. De acordo com a correlação proposta por Horio et al (1980), apresentada por Kunii
e Levenspiel (1991), e já referida no Capítulo 2, equação 2.1,.o cálculo de TDH depende do
diâmetro das bolhas que se formam à superfície do leito. Para poder calcular esse diâmetro
recorreu-se à expressão empírica apresentada por Darton et al (1977), que vem referida por
Rhodes (1998), aplicada a partículas do grupo B, e já apresentada também no Capítulo 2,
equação 2.2 que se transcreve,
d BVS =
0,4
0,54
v
−
v
× hmf + 4 N −0,5
(
)
0
mf
0,2
g
(
)
0,8
(2.2)
em que N é o número de orifícios por unidade de área do distribuidor[m-2]
Determinado o diâmetro equivalente das bolhas à superfície do leito é então possível
estimar o valor de TDH. Para no entanto o poder introduzir na correlação adimensional que se
procura, é preciso desde logo adimensionalizá-lo. Como tem dimensões de comprimento,
basta dividi-lo por uma grandeza com a mesma dimensão, e a que parece ter mais sentido será
precisamente a altura do leito de partículas. A altura do leito é uma variável experimental que
é determinada à custa do valor da pressão do leito.
A correlação a que se chegou foi então:
Nucalc = 2, 08 Re
−0,21
 v
Pr  0
v
 mf



−0,16
 dp 
 
 di 
−0,63
  T −T
 ln  L w
  TL − Tgscorr
 

 


0,25
 TDH

 hmf



0,22
(6.4)
A Figura 6.8 que se segue mostra além dos valores experimentais, os valores calculados pela
equação 6.4
117
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
25
Nucalc
20
15
10
5
0
0
5
10
15
20
25
Nuexp
Figura 6.8- Nucalc pela equação 6.4 versus Nuexp, e 99 observações.
Neste caso o desvio médio obtido foi de Dm=21%.
Como conclusão pode-se dizer que esta correlação relativamente à apresentada no
Capítulo 5, não conduz a melhores resultados no que diz respeito ao desvio médio. Além
disso, a relação empírica que envolve o cálculo de TDH bem como a que permite o cálculo do
diâmetro das bolhas, podem ser de algum modo desajustadas às condições operatórias
utilizadas neste trabalho.
6.2.3 Velocidade média de subida das bolhas
A velocidade média de subida das bolhas através do leito é também uma variável que
estará relacionada com a quantidade de partículas projectadas à superfície do leito. Quanto
maior for essa velocidade, para o mesmo diâmetro de bolhas, maior será o fluxo de partículas
projectado.
De acordo com a teoria das duas fases, que considera que o excesso de gás, (v0-vmf)
passa através do leito sob a forma de bolhas mantendo-se a emulsão nas condições mínimas
de fluidização, a velocidade média de subida das bolhas pode ser prevista pela equação
proposta por Davidson and Harrison (1963) e apresentada por Liang-Shih(1998) que é a
seguinte,
vmb = v0 − vmf + 0, 71 gd BVS
118
(6.5)
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
No entanto para aplicar esta equação é preciso garantir que dBVS/di < 0,6. Para quocientes
superiores a 0,6 os efeitos de parede começam a ser tão significativos, que as bolhas que se
formam podem dar origem ao aparecimento de bolhas tubulares.
Para as partículas de dp=107,5 µm e dp=142,5 µm o valor médio do referido quociente
é 0,8 e 0,7 respectivamente. Para as partículas de dp=180 µm, o valor médio de dBVS/di é 0,6; e
para os dois tamanhos maiores o valor médio de dBVS/di é 0,5. Estes resultados não permitiam
em verdade aplicar a equação acima referida aos dois tamanhos menores de partículas. No
entanto, e dada a proximidade dos valores obtidos com o limite de aplicabilidade, e, de se
pretender apenas uma estimativa da velocidade média de subida das bolhas, procurou-se outro
critério para considerar a possibilidade ou não da formação de bolhas tubulares.
Existem correlações nomeadamente a proposta por Stewart and Davidson (1967)
apresentada por Liang-Shih (1998) que permitem estimar a velocidade mínima do gás
necessária à formação de bolhas tubulares, que podem ocorrer quando o diâmetro das bolhas
atinge valores próximos do diâmetro do leito. A equação proposta é:
vmt = vmf + 0, 07 gdi
(6.6)
Para todos os ensaios e para toda a gama de tamanhos, a velocidade superficial
calculada à temperatura do leito, é sempre superior ao valor de vmt previsto por esta equação,
o que conduziria necessariamente à formação de bolhas tubulares, no entanto, o valor de vmt
não é condição suficiente. Liang-Shih (1998), apresenta uma proposta de Baeyens and Geldart
(1974), em que estes autores consideraram que é preciso que haja uma altura mínima de leito
para assegurar a formação de bolhas tubulares. A expressão proposta é,
H mt = 1,34d i0,175
(6.7)
De acordo com o diâmetro da coluna, o valor de Hmt obtido no caso presente é de 0,8 m,
que é muito superior a todas as alturas de leito com que se trabalhou.
Face a esta análise, vai ser usada a expressão de vmb para estimar a velocidade média de
subida das bolhas para todas as dimensões de partículas usadas. Esse valor vai ser
adimensionalizado dividindo-o por ( v0-vmf ).
Retomando novamente os dados experimentais e introduzindo esta nova variável da
velocidade média de subida das bolhas, a correlação que melhor ajusta estes dados
experimentais é
119
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
Nucalc
 v
= 7, 2 Re −0,12 Pr  mb
v −v
 0 mf



−0,22
 dp 
 
 di 
−0,35
  T −T
w
 ln  L corr
  TL − Tgs
 

 


0,19
(6.8)
Pela figura que se segue pode ser visualizada a relação entre valores de Nu experimentais e
calculados,
25
Nucalc
20
15
10
5
0
0
5
10
Nuexp
15
20
25
Figura 6.9 Nucalc pela equação 6.8 versus Nuexp, e 99 observações.
O desvio médio obtido foi neste caso de Dm = 19%, que é idêntico mais uma vez ao obtido
com a equação 5.17.
6.2.4 Coeficiente de dispersão vertical
O coeficiente de dispersão vertical Ddv pode também ser uma medida da maior ou menor
projecção de partículas que vai acontecer à superfície do leito, já que pretende quantificar o
arrasto das partículas mais finas devido ao movimento ascendente das bolhas. Há correlações
que procuram estimar este coeficiente. Uma delas é apresentada por Kunii e Levenspiel
(1991), e ajusta bastante bem os dados experimentais de vários autores, dentro da gama de
velocidades superficiais com que se trabalhou no presente estudo 0,2< v0 (m/s)<0,5. A
equação é:
Ddv = 0, 3di0,65
120
(6.9)
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
De acordo com a dimensão do leito usado o coeficiente de dispersão vertical é
Ddv = 0,045 m2/s. É este valor, que sendo dividido pelo factor vmbhL permite obter uma nova
variável adimensional que mais uma vez é inserida na correlação de ajuste procurada.
O resultado obtido foi o seguinte:
Nucalc
 v
= 4, 2 Re−0,23 Pr  0
v
 mf



−0,12
 dp 
 
 di 
−0,57
  T −T
 ln  L w
  TL − Tgscorr
 


 

0,25
 Ddv 


 vmb hL 
0,023
(6.10)
A figura que se segue mostra também valores experimentais e calculados e a sua
proximidade relativa
25
Nucalc
20
15
10
5
0
0
5
10
Nuexp
15
20
25
Figura 6.10 Nucalc pela equação 6.10 versus Nuexp, e 99 observações.
O desvio médio obtido foi neste caso de Dm = 19%.
6.3 Conclusão
Foram aqui analisadas quatro variáveis que influenciam a quantidade de partículas
projectadas da superfície do leito para a parede interior do permutador são elas:
- v0/(v0-vmf)
- TDH
- vmb
-
Ddv
As quatro correlações obtidas conduzem a desvios médios muito semelhantes e por isso
o valor do Dm não é um factor que permita escolher de entre elas a melhor. Além disso se for
121
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
comparado qualquer um destes resultados com o obtido no Capítulo 5, equação 5.17, também
aqui se nota a semelhança obtida. Neste caso a correlação que oferece maior confiança é a que
envolve a variável v0/(v0-vmf) porque esta é uma variável experimental, ao contrário das outras
que envolvem correlações empíricas para cálculo de variáveis que podem de alguma forma
não serem aplicadas às condições concretas de operação.
As Tabela 6.1 e 6.2 que se apresentam de seguida pretendem resumir o estudo até aqui
feito, no que diz respeito às correlações encontradas, desvio médio e limites de aplicabilidade.
Na Tabela 6.1 resumem-se as 5 correlações encontradas para toda a gama de partículas com
que se trabalhou, sendo a primeira correlação apresentada a equação geral para os ensaios sem
combustão, equação 5.17, com propriedades avaliadas a Tf. As outras quatro, em que as
propriedades do ar são avaliadas à TmL-w são as correspondentes ás equações, 6.3; 6.4, 6.8 e
6.10, em que a variável v0/vmf é substituído por v0/(v0-vmf) e por vmb/(v0-vmf ) respectivamente
em 6.3 e 6.8, e, em 6.4 e 6.10 se introduz mais uma variável ligada à projecção das partículas
que é respectivamente TDH/hmf e Ddv/(vmb.hmf).
Na Tabela 6.2 são apresentadas as duas correlações obtidas tendo em atenção o diferente
comportamento observado para as duas dimensões mais pequenas de partículas relativamente
às três maiores. Para as duas equações 6.1 e 6.2 referidas nesta tabela as propriedades do ar
foram avaliadas à Tf .
Tabela 6.1 Correlações empíricas para 107,5 < dp(µm) < 357,5 e Pr = 0,73
Correlações empíricas
Nucalc = 14, 7 Re
Nucalc = 0, 77 Re
Nucalc = 2,08Re
122
−0,13
−0,21
Nucalc = 7, 2 Re
Nucalc = 4, 2 Re
−0,35



−0,09
 v0
Pr 

 v0 − vmf
v
Pr  0
 vmf

−0,12
−0,23
 v
Pr  0
 vmf




−0,16



−0,12
0,78
 dp 
 
 di 
 v
Pr  mb
 v0 − vmf

 v
Pr  0
 vmf







 dp 
 
 di 
 dp 
 
 di 
 dp 
 
 di 
−0,63
−0,22
−0,47
−0,69
  T −T
w
 ln  L corr
  TL − Tgs
 
  T −T
 ln  L w
  TL − Tgscorr
 
 dp 
 
 di 
−0,57
  T −T
w
 ln  L corr
  TL − Tgs
 
−0,35
0,25

 




 

0,25

 


Limites de Rear
18
200 < Rear < 400
19
150 < Rear < 350
21
150 < Rear < 350
19
150 < Rear < 350
19
150 < Rear < 350
0,21
0,24
0,22
 TDH 


 hmf 
  T −T
w
 ln  L corr
  TL − Tgs
 
  T −T
 ln  L w
  TL − Tgscorr
 

 


Dm (%)

 


 Ddv 


 vmb hL 
0,19
0,023
6. Considerações sobre o comportamento das partículas relativamente ao calor transferido
Tabela 6.2 Correlações empíricas para 107,5 < dp(µm) < 142,5 e para 180 < dp(µm) < 357,5 e
Pr = 0,73
dp
(µm)
107,5 a 142,5
180 a 357,5
Dm
Correlações empíricas
Nucalc = 0, 058 Re
0,24
 v
Pr  0
v
 mf
Nucalc = 0,38 Re
0,22



0,38
 dp 
 
 di 
 v
Pr  0
 vmf

−0,58



(%)
  T −T
 ln  L w
  TL − Tgs
 
−0,18
 dp 
 
 di 

 


Limites de Rear
0,13
12
200 < Rear < 350
10
200 < Rear < 400
−0,51
123
7. Transferência de calor com combustão de propano
7.Transferência de calor com combustão de propano
7.1 Introdução
Seguindo o procedimento experimental apresentado no Capítulo 3 passou-se à fase de
ensaios em que se alimenta propano à coluna provocando a sua auto-ignição, face à
temperatura que era imposta ao leito. A reacção de combustão que ocorre, provoca um
incremento da transferência de calor para a água de arrefecimento, que circula na camisa, em
relação ao calor transferido na ausência de combustão. Esta fase experimental vai permitir um
estudo dos mecanismos de transferência de calor que ocorrem no permutador de calor, na
presença de reacção e comparar as várias granulometrias de areia quanto ao seu
comportamento na progressão da referida reacção.
Como já foi referido no Capítulo 5 e de acordo com os gráficos aí apresentados, as
condições de operação dizem respeito, para todas as partículas, a um escoamento no leito que
apresenta características de borbulhante para a toda a gama de caudais de ar usados, não
havendo portanto para todos os tamanhos testados circulação de sólidos. Contudo o quociente
vo/vmf para a mesma temperatura do leito e para o mesmo caudal mássico de ar circulante, é
muito diferente quando o leito é constituido pelas partículas mais pequenas ou quando é
formado pelas de maior dimensão. O referido quociente, para uma temperatura do leito de
700 ºC e um caudal de ar de 1 kg/h, varia desde 40 até 4 quando a granulometria passa de
107,5 µm para 352,5 µm respectivamente. Ora esta diferença vai ter influência na maneira
como a reacção de combustão evolui e consequentemente na taxa de transferência de calor
para a água.
Uma outra característica desta fase de ensaios com reacção química, é a constatação da
existência de transporte de partículas ao longo do permutador. Este transporte, que é detectado
pela variação de pressão que ocorre no leito durante o decorrer da combustão, é devido à
125
7. Transferência de calor com combustão de propano
influência das explosões decorrentes da reacção de combustão e não propriamente por se
conseguir atingir no leito um regime de fluidização rápida, necessária à circulação de sólidos.
Para que este estudo de transferência de calor permita comparar as várias granulometrias
de areia usadas, é preciso então que as condições de arranque da reacção sejam semelhantes
em todos os ensaios efectuados e para toda a gama de tamanhos usados. Deste modo, optou-se
por usar um caudal de ar de 1 kg/h e uma temperatura do leito de 720 ºC, para
estabelecimento das condições de arranque antes da alimentação do propano. Tendo em
atenção as limitações físicas da instalação, que já foram referidas, e o facto de não se ter
conseguido atingir, para o caudal de ar de 1kg/h, a temperatura de 720 ºC, quando se
trabalhou com as partículas dp=107,5 µm, houve necessidade de diminuir o caudal de ar para
valores na ordem de 0,85 kg/h, para que fosse possível atingir a temperatura mínima
necessária à auto-ignição do propano. Depois de se ter iniciado a combustão nestas condições,
aumentou-se devagar o caudal de ar para o valor de 1kg/h e tentou-se aguentar a combustão o
máximo de tempo possível. Para todas as outras gamas de tamanhos de partículas, as
condições de arranque foram feitas com o caudal de ar de 1 kg/h, no entanto, para o caso das
partículas de dp=142,5 µm e, para poder comparar resultados relativamente às de menor
dimensão, optou-se por também iniciar alguns ensaios com o caudal de ar de 0,85 kg/h. Para
as partículas de dp=180 µm, dp=282,5 µm e dp=357,5 µm trabalhou-se também com caudais
de ar de 1,2 kg/h.
Os sinais indicativos da progressão da reacção foram o barulho que se ouvia e a
ausência de cheiro. Quando se começava a sentir cheiro intenso, a hidrocarbonetos não
queimados, era sinal que o propano não estava a arder e era necessário fechar imediatamente a
válvula de alimentação de propano. Depois de se cortar o propano e dar como terminada a
reacção de combustão, o procedimento experimental foi idêntico ao que se indicou no
Capítulo 3.
A maioria dos ensaios são feitos para um caudal de água de 73 kg/h não havendo
necessidade de voltar a analisar a influência do caudal de água no processo de transferência de
calor. Como já foi dito a resistência dominante na transferência de calor encontra-se do lado
interior do permutador.
Apresentam-se de seguida os resultados obtidos para as várias granulometrias no que diz
respeito à variação de entalpia da corrente gasosa e da água, no decorrer de cada ensaio que
engloba as seguintes etapas:
- Estabelecimento das condições de arranque;
126
7. Transferência de calor com combustão de propano
- Início da combustão com a alimentação de propano;
- Corte de propano;
- Estabelecimento de novo estado de equilíbrio com o mesmo caudal de ar a circular e
com a resistência eléctrica ligada;
- Corte de ar;
- Evolução da variação da entalpia da água para um estado pseudo-estacionário.
Também são aqui apresentados gráficos elucidativos da evolução do perfil de
temperaturas do lado dos gases bem como a variação de pressão no leito ao longo de todo o
ensaio, nos casos em que essa variação foi notória.
7.2 Resultados experimentais para as partículas de areia com dp=107,5 µm
Estabeleceram-se as condições de arranque para uma temperatura do leito de 720ºC e
para um caudal de ar de cerca de 0,85 kg/h. Depois de atingido um estado de equilíbrio
aumentou-se o caudal de ar para 1 kg/h.
Apresentam-se de seguida, sob a forma de tabela, os valores médios dos resultados
obtidos para dois dos vários ensaios feitos que são exemplificativos de todos os outros. De
seguida, para melhor visualizar a evolução do valor das variáveis durante as diferentes fases
do ensaio apresentam-se os gráficos respectivos.
Os resultados obtidos para todos os ensaios feitos são apresentados no Apêndice V.
Tabela 7.1 Valores médios para qgas e qag no ensaio com combustão; dp = 107,5 µm; caudal de água de
73 kg/h.
dp=107,5
TL
Tgecorr
Tgscorr
Tw
µm
(ºC)
(ºC)
(ºC)
Arranque
718
499
Combustão
722
Combustão
719
PL
mar
mpro
(ºC)
(cm)
(kg/h)
(kg/h)
93
33
9,5
0,85
741
100
40
9.0
762
281
53
4,4
qag
qgas
(W)
(W)
34
317
105
9
35
597
219
10
40
1043
192
A/C
v0/vmf
-----
-----
0,85
0,095
1,0
0,1
127
7. Transferência de calor com combustão de propano
De seguida apresentam-se as figuras correspondentes aos valores referidos nas Tabela 7.1
1000
Potência térmica (W) e T
L
(ºC)
1200
800
600
400
200
t1
t3
t2
t4
0
0
1000
2000
3000
4000
5000
6000
tem po(s)
Tleito
calor agua
calor ar
Figura 7.1 Variação da entalpia da corrente gasosa e da água para um ensaio com combustão do
propano. t1 – introdução do propano ao caudal de 0,095 kg/h; t2 - aumento do caudal de ar
para 1kg/h sem aumentar o propano; t3 - corte de propano; t4 – corte de ar; dp=107,5 µm
A Figura 7.2 abaixo, refere-se à variação de pressão no leito durante o respectivo ensaio,
podendo ver-se que essa variação de pressão só tem início praticamente aos 2000 s, altura em
que se aumenta o caudal de ar para 1 kg/h.
12
PL (cm de H2O)
10
8
6
4
2
0
0
1000
2000
3000
4000
5000
tempo(s)
Figura 7.2.- Variação da pressão no leito versus tempo; dp=107,5 µm.
128
7. Transferência de calor com combustão de propano
A Figura 7.3 refere-se agora à evolução dos perfis de temperatura do lado dos gases,
Tg (ºC)
1000
800
TL
600
Tge
400
200
Tgs
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Figura 7.3 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.1; dp=107,5µm.
O ensaio que se apresenta de seguida diz respeito ao caudal de água de 35 kg/h e, neste
caso, não se conseguiram atingir condições de estado pseudo estacionário relativamente ao
arranque da combustão com o caudal de ar de 0,85 kg/h. Não se apresenta o gráfico da
variação da pressão no leito durante o processo de combustão porque neste caso não foi
evidente essa variação, houve apenas algumas oscilações.
Tabela 7.2 Valores médios para qgas e qag no ensaio com combustão; dp = 107,5 µm.; caudal de água de
35 kg/h
dp=107,5
TL (ºC)
µm
Tgecorr
Tgscorr
Tw
PL
mar
mpro
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
A/C
v0/vmf
qag
qgas
(W)
(W)
Arranque
720
490
65
31
14
0,82
-----
------
33
211
106
Combustão
-----
-----
-----
-----
-----
0,90
0,09
-----
-----
-----
-----
Combustão
715
790
371
64
14
0,98
0,10
9,8
40
1003
165
129
7. Transferência de calor com combustão de propano
Potência térmica (W) e TL(ºC)
1200
1000
800
600
400
200
t1
t3
t2
t4
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Tleito
calor agua
calor ar
Figura 7.4 Variação da entalpia da corrente gasosa e da água para um ensaio com combustão do
propano. t1 - introdução do propano ao caudal de 0,09 kg/h; t2 - aumento do caudal de ar
para 0,98 kg/h e do caudal de propano para 0,1 kg/h; t3 - corte de propano; t4 - corte de ar;
dp=107,5µm.
Tg (ºC)
1000
800
TL
600
Tge
400
200
Tgs
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Figura 7.5.- Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.2; dp=107,5 µm.
Pela análise das Figuras 7.3. e 7.5. verifica-se, que no momento em que se introduz o
propano para se dar início à reacção de combustão, a temperatura do leito mantém-se
constante, notando-se porém uma subida brusca na temperatura dos gases à entrada do
permutador atingindo valores superiores à temperatura do leito. Apesar disso no ponto de
saída dos mesmos a temperatura também se mantém inalterada. Só quando se aumenta o
130
7. Transferência de calor com combustão de propano
caudal de ar é que a temperatura na saída dos gases sofre um aumento brusco. A variação da
entalpia dos gases sofre um aumento ligeiro quando se inicia a reacção, ver figura 7.1 e 7.4,
mas depois mantém-se praticamente constante. No entanto, o processo de combustão leva a
um aumento substancial da entalpia da água, aumento este que ainda é mais evidente quando
se aumenta o caudal de ar e de propano.
Isto permite concluir que a chama proveniente da reacção de queima foi agora o
principal fenómeno no aquecimento da água. No entanto, a evolução dessa chama que deve
ser formada inicialmente no interior do próprio leito e evoluir até à superfície do mesmo, vai
depender das características hidrodinâmicas do leito de partículas. Por este motivo, mais uma
vez o grau de borbulhamento do leito vai ser o factor mais importante para a evolução da
reacção de queima.
Todos os outros ensaios experimentais progrediram de uma maneira muito semelhante
aos que aqui foram mostrados, pelo que apenas se apresentam os resultados experimentais de
todos eles no Apêndice V. No entanto como conclusão, e para melhor poder comparar os
valores obtidos no que diz respeito à variação das entalpias do ar e da água face aos caudais
de ar e propano usados, apresenta-se um resumo desse mesmos valores na Tabela 7.3.
Tabela 7.3 Valores experimentais para os ensaios de combustão; dp=107,5 µm
qag
qgas
(W)
(W)
35
597
219
10
40
1043
192
0,09
9,6
35
618
226
1
0,09
11
40
1300
179
3ºensaio
0,98
0,1
9,8
40
1003
165
4ºensaio
0,83
0,09
9
34
630
216
0,82
0,098
8,4
34
458
210
0,9
0,098
9
37
853
226
0,83
0,1
8,3
34
642
218
Ensaio
mar
mpro
(kg/h)
(kg/h)
0,85
A/C
v0/vmf
0,095
9
1
0,1
0,85
1º ensaio
2ºensaio
5ºensaio
6ºensaio
131
7. Transferência de calor com combustão de propano
7.3 Resultados experimentais para as partículas de areia com dp=142,5 µm
Como já foi referido na Introdução deste mesmo Capítulo 7, estabeleceram-se as
condições de arranque para uma temperatura do leito de cerca de 720ºC e para um caudal de
ar que começou por ser 1 kg/h. No entanto para se poderem comparar diferentes
granulometrias fizeram-se ensaios em que se começou por estabelecer um caudal de ar de
0,85 kg/h e, só depois de atingido um estado de equilíbrio, este foi aumentado para 1 kg/h.
Apresenta-se de seguida sob a forma de tabela os valores médios dos resultados obtidos
para dois dos vários ensaios realizados, já que a evolução de todos eles foi semelhante,
seguida dos gráficos respectivos para melhor poder visualizar a evolução das várias variáveis
durante as diferentes fases do ensaio.
Este primeiro ensaio correspondeu apenas a um único caudal de ar de 1kg/h.
Tabela 7.4 Valores médios para qgas e qag no ensaio com combustão ; dp = 142,5 µm; caudal de água de
73 kg/h
dp=142,5
TL
Tgecorr
Tgscorr
Tw
PL
mar
µm
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
713
648
248
39
14
1,0
-----
-----
Combustão
717
789
262
46
10
1,0
0,1
10
132
mpro
A/C
qag
qgas
(W)
(W)
20
566
127
19
843
210
v0/vmf
7. Transferência de calor com combustão de propano
Potência térmica (W) e TL(ºC)
1200
1000
800
600
400
200
t1
0
0
1000
t2
t3
2000
3000
4000
TL
Calor água
5000
6000
tempo(s)
calor gás
Figura 7.6 Variação da entalpia da corrente gasosa e da água para o ensaio com combustão do
propano. t1 – introdução do propano ao caudal de 0,1 kg/h; t2 - corte de propano; t3 - corte
de ar; dp=142,5 µm.
20
PL (cm de H2O)
16
12
8
4
0
0
1000
2000
3000
4000
5000
tempo(s)
Figura 7.7 Variação da pressão do leito versus tempo, correspondente à Tabela 7.4; dp=142,5 µm.
133
7. Transferência de calor com combustão de propano
1000
Tg(ºC)
800
TL
600
Tge
400
Tgs
200
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Figura 7.8 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.4; dp=142,5 µm.
O outro ensaio que se optou por apresentar diz respeito a um caudal de água de
35 kg/h. Neste caso o arranque da combustão foi feito para o caudal de ar de 0,85 kg/h, para
se poder comparar os resultados obtidos com os que se obtiveram para dp=107,5 µm.
Tabela 7.5 Valores médios para qgas e qag no ensaio com combustão; dp = 142,5 µm; caudal de água de
35 kg/h
dp=142,5
qag
qgas
(W)
(W)
16
255
102
9,3
16
424
206
9,8
18
806
231
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
µm
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
715
489
82
33
15
0,83
-----
-----
Combustão
719
710
95
40
15
0,83
0,09
Combustão
712
783
195
56
11
0,98
0,1
A/C
v0/vmf
Mostram-se de seguida os gráficos correspondentes a este ensaio de combustão.
134
7. Transferência de calor com combustão de propano
Potência térmica (W) e TL(ºC)
1000
800
600
400
200
t1
t2
t3
t4
0
0
1000
2000
TL
3000
4000
tempo(s)
calor água calor gas
5000
6000
Figura 7.9 Variação da entalpia da corrente gasosa e da água para um ensaio com combustão do
propano. t1 – introdução do propano ao caudal de 0,09 kg/h; t2- aumento do caudal de ar
para 0,98 kg/h sem aumentar o propano; t3 - corte de propano; t4 -corte de ar; dp=142,5 µm.
24
PL (cm de H2O)
18
12
6
0
0
1000
2000
3000
4000
5000
tempo(s)
Figura 7.10 Variação da pressão do leito versus tempo correspondente à Tabela 7.5; dp=142,5 µm.
De seguida apresenta-se a Figura 7.11 que diz respeito aos perfis de temperatura do lado
dos gases.
135
7. Transferência de calor com combustão de propano
1000
Tg (ºC)
800
TL
600
400
Tge
200
Tgs
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Figura 7.11 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.5; dp=142,5 µm
Pela análise quer dos gráficos da variação da entalpia das duas correntes, Figuras 7.6 e
7.9, quer da evolução da temperatura do lado dos gases, Figuras 7.8 e 7.11, pode-se constatar
a semelhança de comportamento no decorrer da reacção de combustão para as duas
granulometrias mais baixas.
A título comparativo apresenta-se na Tabela 7.6 o resumo dos resultados obtidos para os
vários ensaios com as partículas de dp=142,5 µm
Tabela 7.6 Valores experimentais para os ensaios de combustão com as partículas de dp=142,5 µm
Ensaio
mar(kg/h)
mpro(kg/h)
A/C
v0/vmf
qag (W)
qgas (W)
1º ensaio
1
0,1
10
19
843
210
2ºensaio
0,97
0,1
9,7
18
800
215
0,83
0,09
9,3
16
424
206
0,98
0,1
9,8
18
806
231
0,84
0,09
9
16
352
196
0,98
0,09
11
18
786
240
0,83
0,1
8,3
16
429
206
0,98
0,098
10
19
857
224
3ºensaio
4ºensaio
5ºensaio
136
7. Transferência de calor com combustão de propano
7.4 Resultados experimentais para as partículas de areia com dp=180 µm
Estabeleceram-se as condições de arranque para uma temperatura do leito de cerca de
720 ºC e para um caudal de ar de 1 kg/h. Depois de atingido um estado de equilíbrio tentou-se
em alguns dos ensaios aumentar o caudal de ar para 1,2 kg/h. Nem sempre isso foi conseguido
porque neste caso era difícil aguentar a reacção de combustão. Trabalhar com caudais de ar
inferiores a 1 kg/h não foi feito neste caso porque, para esta dimensão de partículas e com este
caudal de ar, a quantidade de calor transferida para a água de arrefecimento era muito baixa.
Apresentam-se de seguida as tabelas e os gráficos respectivos de dois ensaios genéricos.
Tabela 7.7 Valores médios para qgas e qag no ensaio com combustão; dp = 180 µm; caudal de água de
73 kg/h
dp=180
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
µm
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
718
505
188
30
9
0,95
Combustão
791
730
117
33
9
Combustão
738
781
219
42
7
qag
qgas
(W)
(W)
19
355
92
10
22
480
242
9,2
24
813
270
A/C
v0/vmf
------
------
1,0
0,1
1,2
0,13
137
7. Transferência de calor com combustão de propano
Potência térmica (W) e T L(ºC)
1000
800
600
400
200
t1
t2
t3
t4
0
0
1000
2000
3000
4000
5000
6000
tem po(s)
TL
calor água
calor gás
Figura 7.12.- Variação da entalpia da corrente gasosa e da água para um ensaio com combustão do
propano (caudal de ar inicial 1kg/h). t1 – introdução do propano ao caudal de 0,1 kg/h; t2 aumento do caudal de ar para 1,2 kg/h e aumento do caudal de propano par 0,13 kg/h; t3 corte de propano; t4 – corte de ar; dp=180 µm.
14
PL (cm de H2O)
12
10
8
6
4
2
0
0
1000
2000
3000
4000
5000
tempo(s)
Figura 7.13 Variação da pressão no leito versus tempo correspondente à Tabela 7.7; dp=180 µm.
138
7. Transferência de calor com combustão de propano
Tg(ºC)
1000
800
TL
600
Tge
400
Tgs
200
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Figura 7.14 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.7; dp=180 µm.
Apresenta-se de seguida um outro ensaio em que as condições de arranque da
combustão foram iniciadas para um caudal de ar de 1,2 kg/h. Neste caso notou-se que a
temperatura do leito se comportou como no caso das duas granulometrias anteriores, ou seja,
manteve-se sempre praticamente igual ao valor de arranque. Não se notou o aumento brusco
dessa temperatura como aconteceu no ensaio anterior, o que significa que a chama deve ter
logo progredido para a superfície do leito.
Tabela 7.8 Valores médios para qgas e qag no ensaio com combustão; dp = 180 µm; caudal de água de
73 kg/h.
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
720
645
125
30
10
1,2
------
------
Combustão
718
832
247
43
7
1,2
0,12
10
dp=180
µm
A/C
v0/vmf
qag
qgas
(W)
(W)
23
340
184
23
850
284
139
7. Transferência de calor com combustão de propano
Potência térmica (W) e TL(ºC)
1000
800
600
400
200
t1
t2
t3
0
0
500
1000
TL
1500
tempo(s)
Calor água
2000
2500
3000
calor gás
Figura 7.15 Variação da entalpia da corrente gasosa e da água para um ensaio com combustão do
propano (caudal de ar inicial 1,2 kg/h). t1- introdução do propano ao caudal de 0,12 kg/h;
t2 - corte de propano; t3- corte de ar; dp=180 µm.
14
PL (cm de H2O)
12
10
8
6
4
2
0
0
500
1000
1500
2000
2500
3000
tempo(s)
Figura 7.16 Variação da pressão no leito versus tempo correspondente à Tabela7.8; dp=180 µm
140
7. Transferência de calor com combustão de propano
1000
Tge
Tg (ºC)
800
TL
600
400
Tgs
200
0
0
500
1000
1500
2000
2500
3000
tempo(s)
Figure 7.17 Perfil de temperaturas corrigidas dos gases correspondente à Tabela7.8; dp=180 µm
A evolução da reacção de combustão e, consequentemente, os perfis de temperatura que
se obtêm do lado dos gases são em tudo semelhante aos obtidos com as partículas de
dp=107,5 µm e dp=142,5 µm. A grande diferença constatada é na temperatura atingida pelo
leito no início da reacção de combustão. É para a dimensão correspondente a dp=180 µm que
se nota uma subida maior e quase instantanea no momento em que se inicia a alimentação do
propano. Isto foi evidente para vários ensaios feitos como o que se mostra na Figura 7.12. No
entanto, também se verificou que quando o arranque da combustão era feito para caudais de ar
de 1,2 kg/h, a temperatura do leito mantinha-se praticamente constante. Isto pode ser
constatado na figura 7.15, sendo então o comportamento do leito semelhante ao obtido para as
dimensões mais pequenas.
A evolução que ocorreu da temperatura do gás à entrada do permutador, foi para as três
dimensões muito semelhante: subiu bruscamente quando se fez a alimentação do propano à
coluna e manteve-se em valores praticamente constantes durante o decorrer da reacção.
Apesar destas diferenças e semelhanças a quantidade média de calor transferida para a
água que circula na camisa é agora bastante mais baixa para as mesmas condições de
operação, relativamente às outras granulometrias, só se conseguindo valores semelhantes para
caudais de ar de 1,2 kg/h.
Mais uma vez se apresenta na Tabela 7.9 o resumo dos resultados obtidos para todos os
ensaios feitos
141
7. Transferência de calor com combustão de propano
Tabela 7.9 Valores experimentais para os ensaios de combustão com as partículas dp=180 µm.
mar
(kg/h)
1
mpro
(kg/h)
0.1
1,2
A/C
v0/vmf
qag (W)
qgas (W)
10
22
480
242
0,13
9,2
24
813
270
1
0.096
10.4
21
457
236
1,2
0,12
10
25
766
295
1
0.098
10.4
23
560
263
1,2
0,13
9,2
24
698
264
1
0,11
9
22
497
243
1
0,12
8,3
21
703
202
5ºensaio
1
0,12
8,3
20
628
275
6ºensaio
1,2
0, 2
10
23
827
276
7ºensaio
1,2
0,12
10
23
850
284
Ensaio
1ºensaio
2ºensaio
3ºensaio
4ºensaio
142
7. Transferência de calor com combustão de propano
7.5 Resultados experimentais para as partículas de areia com dp=282,5µ
µm
Também nestes ensaios a temperatura do leito para as condições de arranque foi mantida
a cerca de 720 ºC e o caudal de ar no valor de 1 kg/h, não se alterando durante o decorrer da
combustão. O caudal de propano mantém-se praticamente constante durante cada ensaio,
embora nalguns ensaios se tenha aumentado ligeiramente para tentar manter a combustão, o
que, nestes ensaios, se tornava bastante complicado.
Para esta granulometria verificou-se que durante o tempo de combustão era difícil obter
do lado da água um estado pseudo-estacionário. Enquanto decorria o processo de queima
havia um aumento muito gradual da variação da entalpia da água, com o leito mantido pela
própria reacção de combustão em temperaturas na ordem dos 800 ºC, o que, mais uma vez,
era sinal de que a reacção se estava a dar no interior do próprio leito. Mas a certa altura o
ruído característico da reacção tornava-se pouco evidente começava a sentir-se mais cheiro e
muitas vezes ouvia-se um “silvo”. Aí, a temperatura do leito começava a baixar e a
temperatura do gás na entrada do permutador sofria uma queda brusca. Embora, dadas as
características da instalação experimental, não fosse possível visualizar a chama, parecia que
esta abandonava rapidamente a superfície do leito e subia ao longo da coluna acabando por se
extinguir devido à baixa temperatura dos gases. No entanto era nesta fase que a potência
calorífica da água aumentava mais rapidamente chegando a atingir um pico, mas como
parecia evidente que a reacção tinha terminado era necessário cortar a alimentação de
propano. A temperatura atingida pelo leito nesta fase, cerca de 700ºC, era disso uma
evidência.
Deste modo, os valores médios apresentados nas tabelas que se seguem dizem respeito a
determinados intervalos de tempo em que se considerou que as condições de combustão,
nomeadamente, os perfis de temperatura do lado dos gases, se mantinham aproximadamente
constantes. Então, o critério para a obtenção dos valores médios abaixo apresentados, foi a
evolução que ocorreu na temperatura do lado dos gases.
Também nestes ensaios foi mais sentido o cheiro resultante de uma queima incompleta e
o ruído característico da combustão foi também muito menor. Por vezes, era necessário
desligar a ventilação do ar para o conseguir ouvir.
Apresentam-se as tabelas correspondentes aos valores médios obtidos para dois ensaios
típicos, mostrando-se para cada um deles a variação das entalpias da água e do gás bem como
a temperatura do leito, e ainda, a evolução dos perfis de temperatura do lado dos gases.
143
7. Transferência de calor com combustão de propano
Não se apresenta a figura da variação da pressão do leito porque nestes ensaios não se
registou qualquer variação. Todos os ensaios feitos para esta granulometria mostram entre
eles uma evolução idêntica, no entanto, algumas diferenças surgiram resultantes da evolução
da reacção de combustão que não se conseguia controlar.
Tabela 7.10 Valores médios para qgas e qag no ensaio com combustão; dp = 287,5 µm; caudal de água
de 73 kg/h
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
718
554
105
27
9
1,0
-----
-----
Combustão
805
583
113
33
9
1,0
0,12
763
367
150
55
8
1,0
0,12
dp=287,5
µm
qag
qgas
(W)
(W)
6,3
282
141
8,6
7,2
539
197
8,6
6,8
1320
87
A/C
v0/vmf
770 a 1400s
Combustão
1420 a 2410s
Potência térmica (W) e T L(ºC)
1600
1400
1200
1000
800
600
400
200
0
0
1000
2000
3000
tem po(s)
TL
calor agua
4000
5000
6000
calor gás
Figura 7.18 Variação da entalpia da corrente gasosa e da água correspondente á Tabela 7.10;
dp=282,5 µm
144
7. Transferência de calor com combustão de propano
1000
TL
Tg (ºC)
800
600
Tge
400
200
Tgs
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
Figura 7.19 Perfil de temperaturas corrigidas dos gases correspondente à Tabela7.10; dp=282,5 µm
O outro ensaio que se mostra de seguida corresponde exactamente às mesmas condições
de arranque, e embora tenha reprodutibilidade como se pode constatar pelos resultados
obtidos, não se conseguiu obter um estado pseudo estacionário para a água.
Tabela 7.11 Valores médios para qgas e qag no ensaio com combustão; dp = 282,5 µm; caudal de água
de 73 kg/h
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
719
579
95
27
10
1,0
-----
-----
Combustão
793
548
103
34
10
1,0
0,12
735
354
155
57
10
1,0
0,12
dp=282,5
µm
A/C
v0/vmf
qag
qgas
(W)
(W)
7,7
285
148
8,3
6,7
571
181
8,3
6,3
1397
81
2480 a 3290 s
Combustão
3490 a 4080s
145
7. Transferência de calor com combustão de propano
1800
Potência térmica (W) e TL(ºC)
1600
1400
1200
1000
800
600
400
200
0
0
1000
2000
3000
4000
5000
6000
tempo(s)
TL
calor água
calor gás
Figura 7.20 Variação da entalpia da corrente gasosa e da água correspondente à Tabela 7.11;
dp=282,5 µm.
1000
Tg (ºC)
800
TL
600
Tge
400
200
Tgs
0
0
1000
2000
3000
4000
5000
6000
7000
tempo(s)
Figura 7.21 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.11; dp=282,5 µm
Como resumo de todos os resultados obtidos para os ensaios feitos com as partículas
correspondentes a dp=282,5 µm, apresenta-se a Tabela 7.12
146
7. Transferência de calor com combustão de propano
Tabela 7.12 Valores experimentais para os ensaios de combustão com as partículas de dp=282,5 µm.
Ensaio
mar
mpro
qag
qgas
(kg/h)
(kg/h)
(W)
(W)
1
7,2
539
197
8,6
6,8
1320
87
0,12
8,3
6,7
571
181
1
0,12
8,3
6,3
1397
81
1
0,095
10,5
6,9
531
155
1
0,095
10,5
6,7
1084
76
1
0,095
10,5
6,2
1210
101
1
0,099
10
6,7
525
189
1
0,099
10
6,5
1020
85
1
0,12
8,3
6,8
537
194
1
0,13
8,1
6,5
1134
103
1.3
0,14
9,3
8,0
1064
163
1,2
0,12
10
8
922
284
1,2
0,12
10
8
1353
162
A/C
v0/vmf
0,12
8,6
1
0,12
1
1ºensaio
2ºensaio
3ºensaio
4ºensaio
5ºensaio
6ºensaio
7.6 Resultados experimentais para as partículas de areia com dp=357,5 µm
As condições de operação são em tudo análogas aos ensaios anteriores: a temperatura do
leito foi mantida a cerca de 720 ºC, o caudal de ar no valor de 1 kg/h e durante cada ensaio
não se alterou o caudal de ar porque, também neste caso, não se conseguia estabilizar a
combustão em termos de obter uma variação da entalpia da água constante. O caudal de
propano manteve-se praticamente constante durante cada ensaio, podendo variar de ensaio
para ensaio entre 0,1 e 0,12 kg/h. Como no caso desta granulometria era possível obter as
condições necessárias ao arranque da combustão para caudais mais altos de ar, trabalhou-se
também com um caudal de ar de 1,2 kg/h e de 1,25 kg/h.
147
7. Transferência de calor com combustão de propano
A evolução dos perfis de temperatura do lado dos gases foi muito semelhante à obtida
com as partículas de dp = 282,5 µm. Isto levou a que o resultado em termos de progressão da
reacção também fosse semelhante, no entanto, neste caso houve ainda mais dificuldade na
obtenção de um estado pseudo-estacionário do lado da água. Assim verificou-se também um
aumento muito gradual da potência calorífica da água, não se atingindo valores constantes,
pouco ruído e algum cheiro característico de uma queima muito incompleta. Também com
esta granulometria pareceu evidente a deslocação da chama característica da reacção de
combustão desde o interior do leito até à zona de transferência de calor.
Da mesma maneira, e dada a dificuldade de obter valores da variação da entalpia da
água durante o processo de queima estáveis com o tempo, os valores dos vários parâmetros
correspondem a valores médios em determinados intervalos de tempo. Deste modo, para
intervalos de tempo em que se verificavam condições relativamente estáveis no leito em
termos de evolução de temperatura, calcularam-se os valores médios das várias variáveis que
a seguir aparecem tabeladas.
Apresentam-se as tabelas correspondentes aos valores médios obtidos, mostrando-se
para dois dos ensaios feitos, a variação das entalpias da água e do gás bem como a
temperatura do leito, e ainda, a evolução dos perfis de temperatura do lado dos gases.
Também neste caso não foi registada qualquer alteração da pressão do leito pelo que não se
apresentam os gráficos respectivos. Todos os ensaios feitos para esta granulometria mostram
entre eles uma evolução idêntica, com as diferenças decorrentes de uma evolução da reacção
de combustão que não se podia controlar. No entanto os resultados apresentaram
reprodutibilidade.
Tabela 7.13 Valores médios para qgas e qag no ensaio com combustão; dp = 357,5 µm; caudal de água
de 73 kg/h
dp=357,5
µm
Arranque
Combustão
qag
qgas
(W)
(W)
4,6
344
159
9
4,3
566
195
10
4,3
1276
98
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
719
579
104
29
9
1,1
------
------
765
570
104
34
9
1,0
0,11
750
379
139
53
9
1,0
0,10
A/C
v0/vmf
518 a 1044s
Combustão
1328 a 1834s
148
7. Transferência de calor com combustão de propano
1800
Potência térmica (W) e TL(ºC)
1600
1400
1200
1000
800
600
400
200
0
0
1000
2000
3000
4000
tempo(s)
TL
calor água
5000
6000
7000
calor gás
Figura 7.22 Variação da entalpia da corrente gasosa e da água correspondente à Tabela 7.13;
dp=357,5µm.
1000
TL
Tg (ºC)
800
600
Tge
400
200
Tgs
0
0
1000
2000
3000
4000
5000
6000
7000
tempo(s)
Figura 7.23 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.13; dp=357,5µm..
Neste caso há um aumento da temperatura do leito já depois de se iniciar a reacção de
combustão porque se aumentou ligeiramente o caudal de propano, uma vez que se sentiu que
a reacção não estava a progredir.
O outro ensaio que aqui se refere foi iniciado com um caudal de ar e 1,2 kg/h, e neste
caso, conseguiu-se uma melhor estabilização da reacção de combustão como se pode verificar
pelas figuras que se apresentam.
149
7. Transferência de calor com combustão de propano
Tabela 7.14 Valores médios para qgas e qag no ensaio com combustão; dp = 357,5 µm; caudal de água
de 73 kg/h
dp=357,5
TL
Tgecorr
Tgscorr
Tw
PL
mar
mpro
(ºC)
(ºC)
(ºC)
(ºC)
(cm)
(kg/h)
(kg/h)
Arranque
715
505
198
29
9
1,2
Combustão
825
585
157
36
9
785
355
179
58
9
1000
2000
3000
µm
qag
qgas
(W)
(W)
4,8
362
109
10
5,7
625
199
10
5,3
1366
81
A/C
v0/vmf
-----
-----
1,2
0,12
1,2
0,12
1400 a 2170s
Combustão
2300 a 3060s
Potência térmica (W) e TL(ºC)
1800
1500
1200
900
600
300
0
0
4000
5000
6000
7000
8000
tempo(s)
TL
calor água
calor gás
Figura 7.24 Variação da entalpia da corrente gasosa e da água correspondente à Tabela 7.14;
dp=357,5µm.
150
7. Transferência de calor com combustão de propano
1000
Tg (ºC)
800
TL
Tge
600
400
Tgs
200
0
0
1000
2000
3000
4000
5000
6000
7000
8000
tempo(s)
Figura 7.25 Perfil de temperaturas corrigidas dos gases correspondente à Tabela 7.14; dp=357,5µm.
Como se pode verificar pelas Figuras 7.23 e 7.25 embora a temperatura do leito se
consiga
aguentar alta durante algum tempo, a temperatura dos gases à entrada sobe
instantaneamente no início da combustão e depois desce rapidamente. Isto significa que a
chama se encontra no interior do próprio leito, provocando o aquecimento dos gases, mas
transferindo pouco calor por radiação para a água de arrefecimento. Só quando a chama se
começa a deslocar para a zona de transporte é que o aquecimento da água vai aumentar muito,
mas a reacção termina devido às baixas temperaturas que aí se registam. Nessa altura é
necessário cortar a alimentação de propano e verifica-se então uma nova subida da
temperatura do leito e dos gases à entrada.
Como de costume, apresenta-se na tabela seguinte todos os resultados obtidos para as
partículas com dp=357,5 µm.
151
7. Transferência de calor com combustão de propano
Tabela 7.15 Valores experimentais para os ensaios de combustão com as partículas de dp=357,5 µm.
Ensaio
1º ensaio
2ºensaio
3ºensaio
4ºensaio
5ºensaio
6ºensaio
7ºensaio
8ºensaio
9ºensaio
152
mar(kg/h)
mpro(kg/h)
A/C
v0/vmf
qag (W)
qgas (W)
1
0,11
9
4,6
566
195
1
0,1
10
4,3
1276
98
1
0,1
10
4,8
560
168
1
0,1
10
4,1
1607
59
1,2
0,12
10
5,7
625
199
1,2
0,12
10
5,3
1366
81
1
0,1
10
4,6
682
191
1
0,1
10
4,2
1367
122
1
0,1
10
4,6
508
208
1
0,11
9
4,1
1343
66
1.2
0,12
10
5,6
672
266
1.2
0,12
10
5,2
1356
144
1
0,12
8,3
4,9
539
189
1
0,11
9
4,5
1407
74
1
0,11
9
4,8
481
198
1
0,1
10
4,4
1460
72
1,25
0,11
12
6,0
607
234
1.25
0.11
12
5.5
1408
84
7. Transferência de calor com combustão de propano
7.7 Análise dos resultados experimentais obtidos para todas as partículas nas condições
de combustão.
7.7.1 Calor transferido para a água durante a reacção de combustão para as diferentes
granulometrias
Depois da apresentação, nos itens anteriores deste mesmo capítulo, de todos os
resultados experimentais obtidos para as cinco granulometrias estudadas, e tendo em conta
que as condições experimentais no que diz respeito aos parâmetros estabelecidos como:
- Temperatura do leito para condições de arranque;
- Caudal de ar;
- Caudal de propano;
- Pressão de arranque.
foram mantidas constantes, é importante fazer uma análise prévia comparativa em termos do
calor transferido para a água de arrefecimento. É importante verificar a sua variação ao longo
do decorrer da reacção de combustão para cada ensaio e para os diversos tamanhos.
A primeira constatação importante e evidente em todos os ensaios feitos, foi a grande
diferença encontrada na evolução da reacção de combustão para as diferentes granulometrias.
Uma vez que os caudais de ar e de propano e, consequentemente, a relação A/C, foram
mantidos sempre dentro dos mesmos valores, as diferentes progressões da reacção que foram
constatadas devem-se ao grau de borbulhamento que se atinge no leito. Se forem analisadas as
Tabelas 7.3, 7.6, 7.9, 7.12 e 7.15, verifica-se:
- dp=107,5 µm ⇒ 34 < v0/vmf < 40
- dp=142,5 µm ⇒ 16 < v0/vmf < 19
- dp=180 µm1 ⇒ 20 < v0/vmf < 25
- dp=282,5 µm ⇒ 7 < v0/vmf < 8
- dp=357,5 µm ⇒ 4 < v0/vmf < 6
Estas diferenças também permitem explicar, como aliás já foi referido, que no caso das
duas maiores granulometrias seja muito mais facilmente atingida no leito a temperatura de
1
Estes valores mais elevados de v0/vmf devem-se ao facto de se ter atingido temperaturas do leito mais altas no
caso desta granulometria relativamente às duas anteriores.
153
7. Transferência de calor com combustão de propano
720 ºC, necessária à auto-ignição do propano, quando o caudal de ar é de 1 kg/h. Para as duas
dimensões mais pequenas foi necessário fazer cada ensaio em duas etapas. Deste modo para
que as condições de arranque fossem atingidas foi necessário trabalhar inicialmente com
caudais de ar de cerca de 0,85 kg/h para se conseguir atingir no leito a temperatura de 720 ºC.
Depois de deixar estabilizar a reacção de combustão no sentido de obter uma variação da
entalpia da água constante é que se aumentou o caudal de ar e de propano para valores de
1 kg/h e 0,1 kg/h, respectivamente, tentando assim manter a relação A/C constante.
Para as partículas de diâmetro 180 µm, como já não foi necessário partir de caudais de
ar tão baixos e, como além disso se verificou um pequeno acréscimo da entalpia da água
relativamente às condições de ausência de propano, começou por se trabalhar logo com
caudais de ar de 1 kg/h. No entanto, também se fizeram ensaios em duas etapas, aumentado o
caudal de ar para 1,2 kg/h para que a gama de trabalho pudesse ser o mais alargada possível
dentro das limitações da instalação experimental.
Para qualquer uma destas três granulometrias, dp=107,5; 142,5 e 180 µm obtiveram-se
resultados reprodutíveis e a progressão da reacção foi semelhante para as três dimensões, mas
também algumas diferenças surgiram, ou seja:
Semelhanças encontradas
- Conseguiu-se uma estabilização da chama que se deve manter à superfície do leito
dada a evolução que se verificou das temperaturas do lado dos gases.
- Durante o decorrer da reacção verificou-se sempre um abaixamento da pressão no leito
devido a um arrastamento (transporte) de partículas para fora do leito, incrementado
pelas explosões que ocorrem dentro do leito assim como à sua superfície. Esse
abaixamento é uma das causas que leva a que a reacção se extinga, pois a certa altura a
quantidade de areia no leito é muito pequena o que leva a uma destabilização da
chama. A possibilidade de repôr a areia no leito para se conseguir circulação de
sólidos, não foi no entanto viável porque, estando a areia fria, o leito arrefecia
repentinamente e cessava a reacção de combustão.
Diferenças encontradas
- À medida que o tamanho das partículas aumenta a quantidade de calor fornecida à
água de arrefecimento baixou.
- No caso das duas menores granulometrias não se verificou um aumento da temperatura
do leito nem no início da combustão nem no decorrer da mesma em toda a gama de
caudais de ar usados. No entanto, no caso de dp =180 µm, houve um aumento
154
7. Transferência de calor com combustão de propano
acentuado da temperatura do leito no arranque da combustão mas que ocorreu apenas
para caudais de ar de 1 kg/h.
Para os dois tamanhos maiores, a progressão da reacção de combustão foi notoriamente
diferente daquela que ocorreu com as três dimensões mais pequenas e que se acabou de
descrever. Também se conseguiu reprodutibilidade nos resultados e, em alguns casos, atingiuse um estado pseudo-estacionário relativamente à variação da entalpia da água, embora com
alguma dificuldade. Esta constatação pode ser visualizada nas Figuras 7.18, 7.20, 7.22 e 7.24.
Deste modo, todos os ensaios foram conduzidos numa única etapa deixando a reacção
progredir e fechando o propano quando se notava que a reacção terminava. Também se
verificou que durante todos os ensaios não houve variação da pressão do leito. Embora
ocorressem as explosões características da reacção de combustão, estas não eram
suficientemente violentas para provocar o transporte de partículas para fora do leito.
A diferença fundamental encontrada relativamente aos outros tamanhos estudados, foi a
evolução dos perfis de temperatura do lado dos gases. Como se pode constatar pelas Figuras
7.19, 7.21, 7.23 e 7.25, no arranque da combustão há um aumento brusco da temperatura do
leito até valores próximos de 800ºC e até, por vezes, superior. Também nesse instante a
temperatura na zona de entrada do permutador apresenta uma subida acentuada. No entanto, a
variação da entalpia da água pouco aumenta e, ao fim de algum tempo, embora o leito ainda
se mantenha a uma temperatura elevada há uma descida brusca da temperatura de entrada dos
gases no permutador. Apesar disso, começa a verificar-se um maior aumento da entalpia da
água até que é necessário cortar a alimentação do propano porque a reacção termina.
Deste modo, os valores dos vários parâmetros apresentados nas Tabelas 7.10, 7.11, 7.13
e 7.14 referem-se a valores médios obtidos para determinados intervalos de tempo em que as
temperaturas do lado dos gases se mantêm praticamente constantes. Portanto, os valores aí
referidos dizem respeito a fases diferentes da mesma reacção de combustão.
Para estas duas maiores dimensões existem situações de instabilidade da reacção de
combustão. Dada a evolução das temperaturas do lado dos gases parece que neste caso e,
contrariamente ao que aconteceu com os tamanhos mais pequenos, a chama vai-se deslocando
no sentido ascendente e portanto a reacção de combustão vai escapar da zona do leito e
progredir para a zona de transferência de calor. Isto provoca um aumento notável de
transferência de calor para a água de arrefecimento como se pode ver nas Figuras 7.18, 7.20,
7.22 e 7.24. No entanto, esta fase que ocorre nos vários ensaios para leitos com partículas de
155
7. Transferência de calor com combustão de propano
357,5 e 282,5 µm, corresponde a uma situação diferente daquela que aconteceu no caso das
partículas de menor dimensão e, portanto, não pode ser comparável.
Por outro lado, o objectivo do presente trabalho foi o de se (estudar) quantificar a
transferência de calor do leito para paredes de membrana em situações de combustão idênticas
às encontradas em casos reais. Ora, em leitos reais queimam-se combustíveis sólidos de
origem fóssil ou biomassa, tendo lugar as reacções heterogeneas (genericamente,C+½
O2⇒CO) e homogéneas (genericamente, CO+½ O2⇒CO2) na fase densa, de modo que agora,
também nos interessa considerar apenas os casos em que a combustão se dá o mais possível
dentro do leito ou à superfície deste. Mesmo em casos de combustão de sólidos (carvões,
biomassa) em leitos fluidizados circulantes, o primeiro passo das reacções, tem lugar à
superfície das partículas combustíveis no interior da porção borbulhante do leito, enquanto
que acima do leito, na zona de transporte, tem essencialmente lugar fenómenos de pirólise
característicos de combustão incompleta.
Com o actual modo de operação do queimador, estando a combustão a ter lugar no
interior do leito ou logo à superfície deste, tentou-se aproximar as condições de operação o
mais possível das encontradas nos queimadores reais.
Pelos resultados experimentais obtidos parece que se está perante dois grupos diferentes
de partículas no que diz respeito à maneira como a reacção de combustão do propano avança
através de um leito borbulhante de di =0,0545 m, constituído por essas partículas. Em termos
de semelhança de comportamentos pode-se agrupar os dois tamanhos mais pequenos, os dois
maiores e as partículas correspondentes a dp =180 µm fazem de alguma maneira a transição
para a diferença de comportamento que acontece com as duas maiores dimensões.
Para melhor visualizar aquilo que se acaba de expor apresenta-se de seguida a Figura
7.26 onde se mostra os valores correspondentes à variação da entalpia da água em função do
diâmetro das partículas para mar=1kg/h e mpro= 0,1 kg/h.
156
7. Transferência de calor com combustão de propano
2000
q ag (W)
1600
1200
800
400
0
0
100
200
300
400
dp(µm)
dp=107,5
dp=142,5
dp=180
dp=282,5 combustão em fase gasosa
dp=357,5 combustão em fase gasosa
dp=282,5
dp=357,5
Figura 7.26 Valores médios da variação da entalpia da água em função do diâmetro das partículas para
mar=1kg/h e mpro=0,1 kg/h.
Como se pode verificar para as partículas dp=282,5 µm e dp=357,5 µm, aparecem dois
conjuntos de pontos. Os que correspondem a valores de qag mais baixos são os obtidos para as
condições de combustão em que a chama ainda permanece no leito - condições iniciais de
combustão.
Estes mesmos resultados também podem ser expressos em termos de um gráfico de
barras, se for determinado para cada granulometria o valor médio correspondente aos valores
médios apresentados na Figura 7.26. Essa determinação é apenas feita para as condições
iniciais de combustão, pois são essas que se poderão comparar. Aproveita-se o mesmo gráfico
para apresentar também os resultados obtidos para condições iniciais de combustão no caso
de mar=1,2 kg/h e mpro=0,12 kg/h. No entanto, estes últimos resultados apenas foram possíveis
para as partículas de dp=180; 282,5 e 357,5 µm
157
7. Transferência de calor com combustão de propano
1200
1
1000
1
qag(W)
800
1,2
1,2
1,2
600
1
1
1
400
200
0
107,5
142,5
180
282,5
357,5
dp (µm)
Figura 7.27 Variação de qag para as diferentes granulometrias e para dois caudais de ar diferentes
sendo A/C =10.
Apresenta-se também o gráfico de barras para os resultados obtidos para as duas
dimensões de partículas mais pequenas no caso mar =0,85 e 1 kg/h e mpro=0,09 e 0,1 kg/h
respectivamente
1200
1
1000
1
qag(W)
800
0,85
600
0,85
400
200
0
107,5
142,5
dp(µ m)
Figura 7.28 Variação de qag para as diferentes granulometrias e para dois caudais de ar diferentes
sendo A/C = 9.4 e A/C = 10
158
7. Transferência de calor com combustão de propano
7.7.2 Análise da tendência do Número de Nusselt para as diferentes granulometrias
durante a reacção de combustão
Tal como foi feito no Capítulo 5, também este capítulo tem como um dos principais
objectivos determinar uma correlação empírica para o valor do coeficiente global de
transferência de calor de um leito borbulhante para as paredes de um permutador de parede de
membrana na presença de uma reacção de combustão. Pretende-se também exprimir esse
coeficiente em termos do número de Nusselt e, para que todas as variáveis possam ser
englobadas na correlação procurada, esta deve ser expressa em termos de grupos
adimensionais apropriados, aliás como já foi feito na ausência de combustão.
Face aos resultados experimentais apresentados no ponto anterior, que mostram
diferentes evoluções da reacção de combustão consoante a granulometria que constitui o leito,
é então importante fazer uma análise prévia comparativa em termos do número de Nusselt
experimental. Assim, deve ser verificada a sua variação ao longo do decorrer da reacção de
combustão para cada ensaio e para os diversos tamanhos, e só depois procurar efectivamente a
correlação empírica adequada.
Tal como já foi feito, o cálculo de Nuexp envolve em primeira instância o cálculo de
hgloexp que vai ser baseado, por uma questão de coerência, no valor de ∆TlnL-w. Depois disso, é
preciso adimensionalizar o valor de hglo tendo em atenção o diâmetro interior do leito e a
avaliação da condutibilidade térmica da corrente gasosa, que neste caso corresponde a uma
mistura de vários componentes gasosos.
No Apêndice IV é feita uma análise das fracções molares dos vários componentes
presentes na reacção de combustão do propano, para as diferentes temperaturas atingidas no
leito durante a evolução da reacção e para diferentes valores da riqueza da mistura-r. Como se
pode constatar dos valores aí apresentados, o número de moles dos diferentes componentes
para a gama de operação deste trabalho variou muito pouco. Assim, consideraram-se os
valores das fracções molares constantes e apresentam-se na Tabela A.IV.4.
Por outro lado é preciso também avaliar o valor das propriedades da mistura gasosa, já
definida em termos de composição, com a temperatura. Como também já foi feito, todas as
propriedades vão ser avaliadas à temperatura do filme e os resultados são apresentados no
Apêndice.IV.
Tendo em conta todas estas considerações apresenta-se de seguida a Figura 7.29 onde se
pretende visualizar a variação de Nuexp com a temperatura do leito para todos os ensaios feitos.
159
7. Transferência de calor com combustão de propano
60
50
Nuexp
40
30
20
10
0
700
720
740
760
780
800
820
840
860
TL(ºC)
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=282,5 combustão em fase gasosa
dp=357,5
dp=357,5 combustão em fase gasosa
Figura 7.29 Valores médios de Nuexp versus TL para todos os ensaios realizados com combustão.
Como se pode constatar, os pontos experimentais que correspondem a valores de Nuexp
mais altos são os obtidos para as duas maiores granulometrias. Como já foi referido para estas
duas granulometrias, além de ser difícil atingir um estado pseudo–estacionário no que diz
respeito à variação da entalpia da água, há uma evolução diferente da reacção durante o
processo de queima, daquela que acontece para os três menores tamanhos. Para dp=282,5 e
357,5 µm, pela análise da evolução da temperatura do lado dos gases, verifica-se que a chama
se vai deslocando para cima à medida que a reacção prossegue, atinge a zona de transferência
de calor e acaba por se extinguir devido ao abaixamento de temperatura que aí ocorre. Deste
modo, e uma vez que não se possuem termopares na zona de transferência de calor
correspondente ao lado dos gases e, portanto, não se dispõem de temperaturas fiáveis, esses
pontos experimentais não podem nem devem entrar na previsão de uma correlação apropriada
para o cálculo do valor de Nusselt, já que correspondem a uma queima em circunstâncias
diferentes.
Deste modo apresenta-se de seguida a Figura 7.30 onde se podem visualizar todos os
pontos experimentais que vão ser usados na procura da correlação apropriada e que
correspondem a todas as granulometrias estudadas e, a situações de combustão localizadas no
interior ou à superfície do leito.
160
7. Transferência de calor com combustão de propano
30
25
Nuexp
20
15
10
5
0
700
720
740
760
780
800
820
840
860
TL(ºC)
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 7.30 Valores médios de Nuexp versus TL para todos os ensaios realizados correspondentes à
mesma fase de queima de propano.
7.7.3 Correlação empírica geral
Sabendo a composição da mistura gasosa em termos de fracções molares dos diversos
componentes, calculando as propriedades da mistura à temperatura do filme e conhecendo
também o valor de Nuexp, começou por se testar uma correlação que envolvesse os mesmos
grupos adimensionais apresentados na correlação já obtida para o caso de ausência de
combustão. Os grupos adimensionais são então:
- Número de Nusselt;
- Número de Reynolds;
- Número de Prandtl;
- v0/vmf
- dp/di
- ln((TL-TW)/(TL-Tgscorr))
Neste caso concreto foi englobado mais uma variável que está relacionado com o facto
de se estar em presença de uma reacção de combustão- variável adimensional r, designada por
riqueza da mistura.
A correlação empírica é então da forma:
161
7. Transferência de calor com combustão de propano
Nucal
 v
= a Reb Pr  0

 vmf
c
d
  d p    TL − TW
    ln 
corr

  di    TL − Tgs
e
 f
  r


(7.1)
Esta expressão envolve seis parâmetros que são determinados pelo programa de
optimização –NLREG.
O resultado obtido, foi o seguinte:
Nucal
 v
= 2, 25 Re0,103 Pr  0

 vmf



−0,094
 dp 
 
 di 
−0,38
  T −T
W
 ln  L corr
  TL − Tgs
 

 


0,078
r 0,18
(7.2)
Em termos gráficos pode ser observada na figura que se segue o resultado obtido:
30
Nuexp
25
20
pontos experimentais
15
linha de ajuste
y = 0.996x + 0.085
10
10
15
20
25
30
Nucalc
dp=107,5
dp=142,5
dp=180
dp=282,5
dp=357,5
Figura 7.31 Valores experimentais para todos os ensaios com combustão, ajuste linear de Nucal versus.
Nuexp e 42 observações
Mostra-se na Figura 7.31. a equação da linha de ajuste porque é necessário conhecer o
declive e a ordenada na origem para se poder fazer a análise estatística pelo método de
Vardeman e até pelo método de t de Student.
Esta correlação é válida para areia fluidizada por ar e propano, à pressão atmosférica,
em condições de combustão numa coluna de di =0,0545 m e dentro dos seguintes limites:
162
7. Transferência de calor com combustão de propano
- 107,5 < dp (µm) < 357,5
- 0,85 < mar (kg/h) < 1,2
- 0,09< mpro (kg/h) < 0,12
- 1,4 < r < 1,9
- 257 < Re < 357
- 700 < TL(ºC) < 820
Apesar de se observar uma certa dispersão de resultados o valor obtido para o desvio
médio foi de: Dm= 12%
Também se pode analisar a dispersão dos pontos relativamente à bissectriz do 1º
quadrante se for traçada a partir dela duas rectas que passem na origem dos eixos e que
tenham um desvio relativamente a ela de 20%. O resultado pode ser visto na figura que se
segue:
30
25
20
Nuexp
20%
15
-20%
10
5
0
0
5
10
15
20
25
30
Nucalc
Figura 7.32 Desvio de ±20% relativamente à recta y = x
Apesar dos resultados obtidos serem satisfatórios apresentando desvios da mesma
ordem de grandeza dos já obtidos na ausência de combustão, recorre-se também à análise da
variável estatística Prob(t), calculada pelo programa de optimização “NLREG”. Como já se
referiu essa variável diz respeito à probabilidade do parâmetro estimado ser zero e, quanto
mais próximo de 1 for o seu valor, menos importante é a variável respectiva na correlação
final encontrada.
Assim, pela análise dos valores obtidos de Prob(t) para cada um dos seis parâmetros
introduzidos na correlação, pode ser analisada a importância relativa de cada um deles.
163
7. Transferência de calor com combustão de propano
De acordo com a correlação apresentada, os resultados obtidos para a variável estatística
Prob(t) foram:
Tabela 7.16 Estimativas finais dos parâmetros da correlação 7.2, e, sua importância relativa- método
de optimização “NLREG”.
Parâmetro
Variável
a
Parâmetro
Prob(t)
2,25
0,78
b
Re
0,103
0,82
c
v0/vmf
-0,094
0,46
d
dp/di
-0,38
0,14
e
ln((TL-Tw/(TL-Tgscorr)
0,078
0,12
f
r
0,18
0,52
Pela análise desta tabela pode-se concluir que a variável Re, que correspondente ao
parâmetro b, é a que menos importância tem na correlação obtida. Além disso as mais
importantes referem-se a: dp/di e a ln((TL-Tw)/TL-Tgscorr)). O parâmetro a é um parâmetro
apenas multiplicativo que não diz respeito a nenhuma variável específica, mas que apesar de
ter uma valor de Prob(t) alto deve ser mantido por efeitos de convergência.
Face a esta análise foram testadas outras correlações com o objectivo de obter equações
mais simples. Para cada uma delas foi sempre analisado o valor de Prob(t) de cada parâmetro
e determinado o valor do desvio médio da correlação final obtida face aos resultados
experimentais.
7.7.4 Correlação empírica simplificada
De acordo com o estudo feito no sentido de obter uma correlação empírica mais
simplificada, dados os valores de Prob(t) obtidos para a equação geral 7.2 e apresentados na
Tabela 7.16, a equação final proposta é,
Nucal
164
d
 d p    TL − Tw
= a    ln 
corr

 d i    TL − Tgs
e
 f
  r


(7.3)
7. Transferência de calor com combustão de propano
Esta expressão envolve agora quatro parâmetros que são também determinados pelo
programa de optimização –NLREG.
Estes quatro parâmetros escolhidos estão de acordo com o valor respectivo do parâmetro
Prob(t) apresentado na Tabela 7.16. São as variáveis para as quais corresponde menor valor
de Prob(t) que mais importância têm na correlação final. A única variável que não obedeceu a
este critério, e que podia ser eliminada da equação 7.3 sem trazer grandes alterações, foi a
variável r. No entanto, a opção de a incluir na referida equação deve-se ao facto de ser a única
que está directamente com a presença de uma reacção química.
O resultado obtido, foi o seguinte:
Nucal
d 
= 5, 45  p 
 di 
−0,22
  T −T
w
 ln  L corr
  TL − Tgs
 

 


0,071
r 0,17
(7.4)
O valor do desvio médio foi também de: Dm=12%
Em termos de valores obtidos para Prob(t) os resultados foram:
Tabela 7.17 Estimativas finais dos parâmetros da correlação 7.4 e sua importância relativa- método de
optimização “NLREG”
Parâmetro
Variável
a
Parâmetro
Prob(t)
5,45
2,0x10-3
d
dp/di
-0,22
6,0x10-5
e
ln((TL-TW/(TL-Tgscorr)
0,071
7,1x10-2
f
r
0,17
0,54
Como seria de prever é a variável r que menos importância tem nesta correlação
simplificada, apresentando um valor de Prob(t) muito superior a qualquer uma das outras
variáveis.
7.7.5 Escolha da correlação empírica final
De acordo com todos resultados apresentados e no sentido de obter a correlação mais
simples possível para cálculo do valor de Nusselt, e assim poder determinar o coeficiente
165
7. Transferência de calor com combustão de propano
global de transferência de calor num leito borbulhante a opção seria a correlação simplificada
7.4. É a equação mais simples e em termos de resultados calculados conduz ao mesmo valor
do desvio médio.
Há no entanto outras questões que devem ser consideradas. A correlação apresentada no
Capítulo 5 engloba todos os parâmetros envolvidos na correlação geral 7.2 apresentada no
presente capítulo, ponto 7.7.3, à excepção do parâmetro r que nesse momento não tinha
qualquer razão de ser, porque os resultados experimentais aí tratados referiam-se à ausência
de combustão. Nesse caso todos os parâmetros tinham uma importância relativa da mesma
ordem de grandeza, - ver Tabela 5.1 - e por isso a simplificação da correlação final
apresentada conduziria sempre a valores do desvio médio maiores, o que significava uma
maior dispersão de resultados.
No caso da presença de combustão os ensaios só fazem sentido para temperaturas
superiores à da auto-ignição do propano e, isso, devido às limitações experimentais com que
se deparou, só foi possível numa gama muito apertada de caudais de ar e, consequentemente,
de propano. A utilização de caudais de ar superiores ao valor máximo usado de 1,3 kg/h não
permitia atingir no leito temperaturas de pelo menos 720ºC. Assim, era de esperar que a
variável Re tivesse neste caso muito pouco significado.
Deste modo, e tendo ainda como objectivo final a obtenção de uma correlação que possa
ser mais abrangente e permita correlacionar todos os dados experimentais com e sem a
presença da reacção de combustão do propano, parece ser mais adequado neste momento a
escolha da correlação geral 7.2, apresentada neste capítulo. Apesar de mais complicada e
tendo variáveis que praticamente não influenciam o resultado final, este também não vem de
maneira nenhuma prejudicado. Assim, no ponto que se segue, passa-se a fazer a análise
estatística da correlação geral.
7.7.6 Análise estatística da correlação geral
O desvio médio de 12% na referida correlação é por si uma medida de confiança nos
valores experimentais e calculados. No entanto, e a título de comparação relativamente à
análise estatística feita no caso de ausência de combustão apresenta-se aqui a mesma análise
proposta por Vardeman (1994). Como aí se refere, se os limites de confiança encontrados
englobarem a recta y = x, pode-se considerar que há uma evidência estatística entre valores
observados e calculados. Apesar deste teste ser mais abrangente que o teste de hipóteses de t
de Student também aqui se analisa a confiança na ordenada na origem e no declive.
166
7. Transferência de calor com combustão de propano
Apresenta-se na figura que se segue o resultado do método proposto por Vardeman
(1994). Como se pode verificar os limites traçados com uma confiança de 95% englobam a
bissectriz do primeiro quadrante, o que permite aceitar com esse nível de confiança a
correlação proposta.
30
Nuexp
25
20
15
10
10
15
20
25
30
Nucalc
Figura7.33 Recta de ajuste e limites de confiança de 95% para a correlação empírica 7.2.
Passando agora ao teste de hipótese de t de Student, que permite aceitar com segurança
o ajuste obtido desde que t(A) e t(B) sejam inferiores ao valor de t de Student para um
determinado nível de confiança e (n-2) graus de liberdade, sendo n o número de observações
experimentais.
Os resultados obtidos considerando um nível de confiança de 95% e n = 42 foram:
- para 40 graus de liberdade e 95% de confiança t = 2,02
- t(A) = 0,028
- | t(B) | = 0,025
167
8.Correlação geral para ensaios com e sem combustão
8.Correlação geral para ensaios com e sem combustão.
Tendo em consideração todo o tratamento de dados que foi apresentado no Capítulo 5análise sem combustão- e no Capítulo 7- análise com combustão de propano – este capítulo
tem como principal objectivo a determinação de uma equação empírica que permita
determinar o coeficiente global de transferência de calor, em termos adimensionais, para as
duas situações em simultâneo.
8.1 Comparação dos resultados obtidos para cada granulometria
No entanto, e antes da apresentação da equação acima referida, optou-se por fazer uma
análise de todos os resultados obtidos para cada granulometria de areia com e sem a presença
de propano. Essa análise é apenas feita em termos gráficos para melhor se poder visualizar as
diferenças existentes.
Nas figuras que se seguem mostra-se a variação de Nuexp versus ∆TlnL-w
Partículas com dp=107,5 µm
30
25
Nuexp
20
15
10
5
0
0
100
200
∆TlnL-W
sem combustão
300
400
500
com combustão
Figura 8.1 Variação de Nuexp versus ∆TlnL-w ; dp= 107,5 µm
169
8.Correlação geral para ensaios com e sem combustão
Partículas com dp=142,5 µm
30
25
Nuexp
20
15
10
5
0
0
100
200
∆TlnL-w
sem combustão
300
400
500
com combustão
Figura 8.2 Variação de Nuexp versus ∆TlnL-w; dp= 142,5 µm.
Partículas com dp=180 µm
30
25
Nuexp
20
15
10
5
0
0
100
200
∆TlnL-W
sem combustão
300
400
500
com combustão
Figura 8.3 Variação de Nuexp versus ∆TlnL-w; dp= 180 µm
170
8.Correlação geral para ensaios com e sem combustão
Partículas com dp=282,5 µm
50
Nuexp
40
30
20
10
0
0
100
200
300
400
500
∆TlnL-w
sem combustão
com combustão
Figura 8.4- Variação de Nuexp versus ∆TlnL-w; dp= 282,5 µm
Partículas com dp=357,5 µm
60
50
Nuexp
40
30
20
10
0
0
100
200
∆TlnL-w
sem combustão
300
400
500
com combustão
Figura 8.5- Variação de Nuexp versus ∆TlnL-w; dp= 357,5 µm
Pela análise destas 5 figuras é nítida a diferença de comportamento verificada entre as
várias granulometrias nas duas situações ocorridas.
Para as duas maiores granulometrias e, como já foi referido no Capítulo 7, os ensaios
feitos na presença de combustão evoluíram de uma maneira diferente daquela que ocorreu
171
8.Correlação geral para ensaios com e sem combustão
para as outras granulometrias. Nas Figuras 8.4 e 8.5 os pontos a vermelho não correspondem
todos a ensaios diferentes mas sim a fases distintas da reacção durante o mesmo ensaio. Por
isso aparecem nas referidas figuras rodeados por uma linha a tracejado.
As partículas com dp= 180 µm, e analisando a figura 8.3, também já mostraram uma
tendência de comportamento que de alguma maneira se aproxima do comportamento
correspondente às duas maiores granulometrias. No entanto, a evolução da temperatura do
lado dos gases foi semelhante àquela que ocorreu para as duas dimensões mais pequenas,
como se pode ver nas Figuras 7.14 e 7.17, o que mostra que a reacção se manteve no interior
do leito e na sua superfície. Deste modo, ainda se conseguiram atingir com alguma facilidade
condições de estado estacionário relativamente à variação da entalpia da água, pelo que todos
os pontos são considerados na procura da correlação empírica geral.
8.2 Correlação final e análise estatística
A relação empírica que se procurou considerou todos os valores de Nuexp obtidos para os
ensaios feitos na ausência de combustão e, todos os obtidos na presença da reacção de
combustão do propano, mas que correspondem à mesma fase da referida reacção. Esta fase, é
para todos esses ensaios, aquela em que a combustão se inicia e progride no próprio leito.
Foram analisadas várias correlações, usando o método de optimização NLREG, mas a
que melhor ajustou os dados experimentais obtidos foi:
Nucal
 v
= 17, 3Re −0,24 Pr  0
 vmf




−0,024
 dp 
 
 di 
−0,30
  T −T
w
 ln  L corr
  TL − Tgs
 

 


0,17
r 0,78
(8.1)
Em termos gráficos são apresentados os valores de Nucalc versus Nuexp para as seguintes
situações:
- Ausência de combustão: resultado previsto pela equação (5.17);
- Combustão do propano: resultado previsto pela equação (7.2);
- Considerando as duas situações: resultado previsto pela equação (8.1)
A figura que se segue, mostra todos esses resultados:
172
8.Correlação geral para ensaios com e sem combustão
30
25
Nuexp
20
15
10
y = 0.998x + 0.008
5
0
0
5
10
15
20
25
30
Nucalc
sem combustão eq 5.17
com combustão eq 7.2
equação geral 8.1
Figura 8.6 Valores experimentais com e sem combustão no leito e ajuste linear de Nucal versus Nuexp141 observações.
Nesta figura apresenta-se a recta de ajuste entre pontos calculados e experimentais
porque é necessário o conhecimento da ordenada na origem e do declive para fazer a análise
estatística que vem referida à frente na secção 8.2.1.
Esta correlação é válida para um leito de areia fluidizada, quer por ar, quer na situação
de combustão do propano, à pressão atmosférica, numa coluna de di = 0,0545 m e dentro dos
seguintes limites:
- 107,5 < dp (µm) < 357,5
- 0,85 < mar (kg/h) < 1,2
- 0,09< mpro (kg/h) < 0,12
- 1,4 < r < 1,9; r =1 para ausência de combustão
- 200 < Re < 400
- 400 < TL (ºC) < 820
Apesar de se observar uma certa dispersão de resultados o valor obtido para o desvio
médio foi de,
Dm= 17%
Neste caso também se recorreu à análise da variável estatística Prob(t), calculada pelo
programa de optimização “NLREG”.
173
8.Correlação geral para ensaios com e sem combustão
De acordo com a correlação apresentada- equação 8.1 ,os resultados obtidos para a
variável estatística Prob(t) foram:
Tabela 8.1 Estimativas finais dos parâmetros da correlação 8.1, e sua importância relativa- método de
optimização “NLREG”
Parâmetro
Variável
a
Parâmetro
Prob(t)
17,3
0,34
b
Re
-0,24
0,09
c
v0/vmf
-0,024
0,68
d
dp/di
-0,30
4,6x10-3
e
ln((TL-TW/(TL-Tgscorr)
0,17
1x10-5
f
r
0,78
1x10-5
Também se pode analisar a dispersão dos pontos relativamente à bissectriz do primeiro
quadrante se for traçada a partir dela duas rectas que passem na origem dos eixos e que
tenham um desvio relativamente a ela de 20%. O resultado pode ser visto na figura que se
segue:
30
25
Nuexp
20
15
20%
-20%
10
5
0
0
5
10
15
20
25
30
Nucalc
Figura 8.7 Desvio de ±20% relativamente à recta y = x para a correlação 8.1
174
8.Correlação geral para ensaios com e sem combustão
8.2.1 Análise estatística
O desvio médio de 17% na referida correlação é por si uma medida de confiança nos
valores experimentais e calculados. No entanto, e a título de comparação relativamente a
todas as análises já feitas com e sem combustão, apresenta-se aqui a mesma análise estatística,
usando mais uma vez o método definido por Vardeman (1994). Se limites de confiança
encontrados pelo respectivo método englobarem a recta y = x, pode-se assumir uma evidência
estatística entre valores observados e calculados. De qualquer maneira, e sendo este teste mais
abrangente que o teste de hipóteses de t de Student, mais uma vez se analisa a confiança na
ordenada na origem e no declive pelo respectivo teste.
Na Figura 8.8, verifica-se que a recta de ajuste apresentada na Figura 8.6 coincide com a
bissectriz do primeiro quadrante, e os limites traçados com uma confiança de 95% obtidos
pelo método proposto por Vardeman englobam a respectiva bissectriz. Isto permite aceitar
com uma confiança de 95% a correlação proposta.
30
25
Nuexp
20
15
10
5
0
0
5
10
15
20
25
30
Nucalc
Figura 8.8. Recta de ajuste e limites de confiança de 95% para a correlação empírica 8.1.
Passando agora ao teste de hipótese de t de Student, que permite aceitar com segurança
o ajuste obtido desde que t(A) e t(B) sejam inferiores ao valor de t de Student para um
determinado nível de confiança e (n-2) graus de liberdade, sendo n o nº de observações
experimentais.
Os resultados obtidos considerando um nível de confiança de 95% e n = 141 foram:
- para 139 graus de liberdade e 95% de confiança t = 1,96
- t(A) = 0,0094
- |t(B) | = 0,035
175
9. Considerações sobre o comportamento do leito
9.Considerações sobre o comportamento do leito
9.1 Introdução
De acordo com todos os resultados obtidos nas duas situações estudadas – sem e com
combustão de propano – verificou-se que a variação da entalpia da água era sempre muito
superior à variação da entalpia do ar ou da mistura gasosa, sendo essa diferença ainda mais
acentuada, nos ensaios que decorreram com combustão e, para as partículas de menor
dimensão. Nestes últimos ensaios, apesar do incremento que houve no calor recebido pela
água, a variação da entalpia da corrente gasosa pouco aumentou relativamente à situação de
ausência de combustão. Assim, a combustão do propano vai libertar calor que, por um lado
vai permitir um maior aquecimento do leito e, por outro lado, vai provocar a ocorrência de
explosões à superfície ou no interior do leito, incrementando a quantidade de partículas
projectadas para fora deste, que irão possibilitar uma maior transferência de calor para a
parede de membrana e consequentemente para a água. É também aqui analisado o modelo a
usar no cálculo de hradL. Como se referiu no Capítulo 4 está-se perante uma mistura gasosa
que neste caso concreto, participa na transferência de calor entre o leito e o permutador.
As condições de borbulhamento do leito, e por conseguinte o maior ou menor
espalhamento de partículas, diferiram consoante a granulometria usada, e estão intimamente
ligados à quantidade de calor recebida pela água. Como já se referiu, foram as partículas mais
pequenas que conduziram a graus maiores de borbulhamento e por isso garantiram um maior
aquecimento da água. Apesar disso, em todos os ensaios realizados sem combustão, nunca
houve transporte de sólidos ao longo do permutador porque se verificou que a pressão do leito
se mantinha sempre constante. Apenas se conseguiu um movimento migratório das partículas
desde a superfície do leito, que apesar de voltarem de novo ao leito, transportaram consigo
energia térmica que foi cedida à água através das parede do permutador. Já no caso da
177
9. Considerações sobre o comportamento do leito
segunda fase de ensaios correspondente à presença de propano, houve como se pode analisar
pelas Figuras 7.2., 7.7., 7.10., 7.13. e 7.16., variação da pressão do leito durante a progressão
da reacção de combustão. No entanto essa variação só ocorreu para as três dimensões mais
pequenas.
É então importante analisar e quantificar com algum detalhe a contribuição do leito no
aquecimento da água para as várias situações apresentadas, tendo em atenção dois parâmetros
fundamentais:
O valor do coeficiente de convecção devido às partículas, hpc;
O fluxo de sólidos que ocorre à superfície do leito.
9.2 Determinação de uma correlação para o coeficiente de convecção das partículas, hpct
Os valores do coeficientes de convecção devido ao movimento das partículas para fora
do leito podem ser calculados a partir da equação 4.12, que se transcreve,
exp
hglo
= hgc + hradL + hpc
(4.12)
O valor de hgc é determinado pela equação 4.13 expressa em termos de Nuf, os valores de
hgloexp obtidos para cada ensaio vêm apresentado no Apêndice V nas Tabelas de A.V.6. a
A.V.10 e A.V.16 a A.V 20. Quanto ao valor hradL, é preciso analisar qual o processo mais
adequado a usar no caso dos ensaios com combustão.
Tendo em conta o método de Hottel apresentado no Capítulo 4, e para ter uma ideia dos
valores de hrmp previstos por esse método, considerou-se a temperatura média do filme, tendo
em atenção os vários ensaios com combustão, bem como uma temperatura média da parede e,
recorrendo à equação 4.29, calculou-se o valor de hrmp. O valor obtido foi de 1,03 W/m2K que
é inferior ao calculado pela equação 4.21, conforme se vê na Tabela 9.1. Isto seria de prever,
dadas as baixas concentrações de vapor de água, de dióxido de carbono e de monóxido de
carbono que correspondem a 8%. O azoto que não participa na radiação é o componente que
existe em maior quantidade, sendo a sua concentração da ordem de 61%, como se pode ver no
Apêndice IV, Tabela A.IV.4. Optou-se então, por considerar para todos os ensaios com e sem
combustão, o cálculo de hradL através do modelo proposto no Capítulo 4, usando para isso a
equação 4.21. A gama de variação de hgc e hradL nos ensaios sem e com combustão para todas
as condições de operação, e para todas as granulometrias, foi muito pequena e vem
apresentada na tabela que se segue,
178
9. Considerações sobre o comportamento do leito
Tabela 9.1 Valores máximos e mínimos de hgc e hradL nos ensaios sem e com combustão
hgc e hradL
Sem
Com
(W/m2K)
combustão
combustão
hgc
2,6 a 3,4
3,1 a 3,5
hradL
0,5 a 1,2
1,3 a 1,7
De acordo com os valores experimentais obtidos para hpc, procurou-se encontrar uma
correlação em termos de grandezas adimensionais adequadas, que melhor ajustasse esses
mesmos valores.
Uma das variáveis que está relacionada com a transferência de calor por convecção
devido às partículas e por conseguinte, com o valor de hpc, é sem dúvida o excesso de gás –
v0-vmf – que atravessa o leito sob a forma de bolhas e contribui assim para o movimento das
partículas para fora da superfície do leito. Assim, uma das grandezas adimensionais a usar na
correlação que se pretende estudar foi ( v0-vmf)/vmf. Analisou-se graficamente a variação de hpc,
para todas as granulometrias, versus (v0-vmf)/vmf , considerando os ensaios sem combustão e os
de combustão na mesma fase de reacção. Os resultados obtidos podem ser analisados nas
figuras que se seguem,
18
15
(W/m2K)
hpc
12
9
6
3
0
0
5
10
15
20
25
30
35
40
(v0-vmf)/vmf
107
142
180
282
357
Figura 9.1 Valores experimentais de hpc versus (v0-vmf)/vmf para os ensaios sem combustão.
Como se pode verificar, há uma maior contribuição das partículas para a transferência
de calor, à medida que o diâmetro das mesmas diminui. Como seria de esperar são as
179
9. Considerações sobre o comportamento do leito
partículas mais pequenas que permitem obter coeficientes de convecção maiores, e isso é
devido ao maior grau de borbulhamento atingido, que provoca um maior espalhamento de
partículas à superfície do leito.
Os resultados obtidos com combustão de propano podem também ser analisados na
figura seguinte,
18
hpc (W/m2K)
15
12
9
6
3
0
0
5
10
15
20
25
30
35
(v0-vmf)/vmf
107,5
142,5
180
282,5
357,5
Figura 9.2 Valores experimentais de hpc versus (v0-vmf)/vmf para os ensaios com combustão
Na Figura 9.2 verifica-se que os valores hpc estão acima dos obtidos para os ensaios sem
combustão, como aliás seria de esperar, mas o incremento que se verifica para cada dimensão
é praticamente constante. Também se nota que a variação de hpc com a dimensão das
partículas não é agora tão evidente, o que leva a pensar que o grau de borbulhamento do leito
pode não ser o fenómeno dominante face à presença da chama característica da reacção.
Para as três menores dimensões a reacção dá-se à superfície do leito e a presença da
chama nessa zona, além de poder incrementar o fenómeno de radiação directa da chama para
a parede do permutador, também pode interferir no modelo de radiação proposto. Esta última
hipótese não é no entanto de considerar, uma vez, que foram feitos cálculos relativamente ao
modelo de radiação proposto, considerando alturas diferentes para o disco, que representa o
leito, e em nada afectou o coeficiente de radiação calculado por esse modelo. Resta então
analisar a presença da chama na superfície do leito. Se numa primeira hipótese se poderia
pensar que a chama à superfície do leito seria o principal fenómeno, essa explicação deixa de
ser viável ao analisar o que se passa em termos do comportamento das partículas maiores.
Como já foi dito, para as duas maiores dimensões a chama entra para dentro do leito e desta
180
9. Considerações sobre o comportamento do leito
forma não podia provocar o mesmo aumento em termos de hpc que provocou nas partículas
mais pequenas. Ora como já se referiu, o aumento de hpc que ocorreu relativamente aos
ensaios sem combustão, foi praticamente o mesmo para todas as dimensões. A explicação que
parece mais credível é a seguinte:
- No caso das partículas mais pequenas o aumento de hpc é essencialmente devido ao
espalhamento que ocorre à superfície do leito e é devido quer à hidrodinâmica do leito quer às
explosões que ocorrem e que atiram algumas partículas para fora do leito provocando uma
redução da queda de pressão do leito durante o decorrer da reacção. Embora essa variação
possa parecer pequena ela corresponde na maior parte dos casos a uma alteração da massa do
leito de cerca de 25 a 30%, durante o tempo em que decorre um ensaio. É este movimento
acrescido das partículas a principal causa do aumento de hpc;
- No caso das partículas maiores o borbulhamento devido à hidrodinâmica do leito é
muito menor, não há variação da queda de pressão através do leito que indicie uma perda de
massa deste, mas contudo, estando o leito mais quente as explosões que ocorrem fazem com
que as partículas transportem, nesta situação de combustão, mais energia térmica que é
transferida para á agua, quando chocam com a parede.
Como conclusão, o acréscimo no valor de hpc não parece ser devido à radiação, mas sim
ao transporte de partículas que é incrementado relativamente à situação de ausência de
combustão, pelas explosões que se dão no interior e à superfície do leito.
Na figura que se apresenta de seguida mostram-se os valores experimentais de hpc em
função de (v0-vmf)/vmf para se poderem comparar melhor os ensaios com e sem combustão,
18
12
2
hpc (w/m K)
15
9
6
3
0
0
5
10
15
20
25
30
35
40
(vo-vmf)/vmf
107,5
142,5
180
282,5
357,5
107,5 comb
142,5 comb
180 comb
282,5 comb
357,5 comb
Figura 9.3 Valores experimentais de hpc versus (v0-vmf)/vmf para os ensaios sem e com combustão
181
9. Considerações sobre o comportamento do leito
Face ao resultado apresentado na Figura 9.3, que envolve todos os ensaios feitos com e
sem combustão tentou arranjar-se uma correlação em termos do número de Nusselt e de
grandezas adimensionais adequadas, que melhor ajustasse os resultados obtidos.
De acordo com Molerus (1995), para partículas com dp < 100 µm, o termo de
transferência de calor devido à convecção por parte das partículas é mais importante do que a
convecção do gás e a radiação. Um dos grupos adimensionais que relaciona a importância
relativa dos coeficientes de convecção devido ao gás e às partículas é o número de
Arquimedes. Segundo o mesmo autor, para 105 < Ar < 108 , a convecção devida ao gás é o
fenómeno principal. Para Ar < 100 prevalece a convecção por parte das partículas. Então o
número de Arquimedes foi a outra grandeza adimensional incluída na correlação a estudar.
Além disso, como a correlação procurada envolve valores experimentais obtidos com e sem
combustão, introduziu-se a variável r, o que já foi feito também no Capítulo 8 quando se
procurou uma correlação geral.
Para esta correlação todas as propriedades do ar envolvidas no número de Arquimedes
foram avaliadas à temperatura do filme, mas para o cálculo de v0 e vmf usou-se a temperatura
do leito.
A correlação empírica a determinar é então da forma:
 v0 − vmf
Nu p = a 
 vmf

b

c d
 Ar r

(9.1)
sendo Nup, baseado no diâmetro interno da coluna.
Esta expressão, envolve quatro parâmetros, a, b, c e d, que são mais uma vez determinados
pelo programa de optimização –NLREG.
O resultado obtido, foi o seguinte:
 v0 − vmf
Nu = 53, 7 
 vmf

m
p



−0,23
Ar −0,29 r 0,86
(9.2)
Esta correlação é válida para leitos borbulhantes de areia numa coluna de diâmetro
interno 0,0545 m, dentro dos seguintes limites:
182
9. Considerações sobre o comportamento do leito
- 107,5 < dp(µm) < 357,5
- 400 < TL (ºC) < 836
- 11 < Ar < 1900
Em termos gráficos, o resultado pode ser observado na figura seguinte:
18
15
Nupm
12
9
6
3
0
0
5
10
15
20
25
Nup
Figura 9.4- Valores de Nup versus Nupmpara todas as granulometrias e 121 observações.
O desvio médio obtido foi de Dm = 29%
9.3 Determinação do fluxo de sólidos a partir da superfície do leito - Modelo teórico
Para determinar o caudal de sólidos à superfície do leito em todos os ensaios feitos sem
e com combustão de propano, foi necessário determinar a quantidade de calor cedida à agua
pelas partículas. Essa quantidade é determinada experimentalmente à custa do balanço de
energia correspondente à equação 4.1, que se transcreve de seguida,
q exp
p = qag − q gas − q radL
(4.1)
Por outro lado, sabendo o calor experimental cedido pelas partículas qpexp, é também
possível determinar o caudal total de areia à superfície do leito, recorrendo à variação da
entalpia da areia, na suposição de que as partículas saem do leito à temperatura deste e que
retornam à temperatura da parede,
183
9. Considerações sobre o comportamento do leito
qpexp = ms cs (TL-Tw)
(9.3)
Com os valores experimentais de ms , calculou-se então o valor do fluxo total de sólidos
à superfície do leito, E0 , a partir da área de escoamento, ou seja,
E0 =
ms
Aesc
(9.4)
Com estes valores experimentais obtidos procurou-se uma correlação empírica que
melhor os ajustasse, tendo consciência da dificuldade que existe quer na escolha das variáveis
adequadas, quer na sua quantificação.
Toda a análise que vai ser feita aqui, é baseada em artigos de diversos autores, todos
eles referidos numa publicação de Wen-Ching (2003). Um desses autores, Levy (1983) refere
que o fenómeno de projecção de partículas a partir da superfície de leitos fluidizados para a
zona de transporte está relacionado com a formação das bolhas e a maneira como estas
rebentam à superfície. A Figura 9.5 pretende representar os vários tipos de projecção de
sólidos que podem ocorrer de acordo com a maneira como as bolhas rebentam à superfície do
leito.
esteira
Figura 9.5- Projecção de sólidos à superfície do leito: a) a partir do topo da bolha; b) a partir da esteira
de uma única bolha; c) a partir da esteira de duas bolhas que coalescem, Wen-Ching(2003).
Na impossibilidade de visualizar o tipo de borbulhamento que ocorre neste trabalho, é
necessário recorrer a estudos já feitos, embora a maior parte deles sejam de natureza teórica.
Por exemplo, Pemberton and Davidson (1983), referem que as partículas do grupo B de
acordo com a classificação de Geldart, tendem a ser projectadas a partir da esteira das bolhas
que se formam.
Deste modo uma das variáveis que deve fazer parte do modelo procurado é o diâmetro
das bolhas que se formam no leito. Para poder determinar esse valor é preciso recorrer
também a correlações apresentadas em bibliografia. Uma das que já foi usada, correspondeu à
184
9. Considerações sobre o comportamento do leito
equação apresentada no Capítulo 2, equação 2.2, sendo também usada no Capítulo 6 para
analisar a influência dessa variável na projecção das partículas
Também de acordo com resultados apresentados na publicação de Wen-Ching (2003),
referida anteriormente, Geldart (1983), referiu que para escoamentos em regime laminar, que
são característicos de instalações à escala piloto, enquanto que as partículas maiores podem
ser arrastadas pela zona central, as mais finas caem junto à parede, e este efeito é muito mais
pronunciado para perfis de velocidade laminares do que turbulentos. Uma vez que não se
verificou qualquer variação de pressão no leito durante todos os ensaios sem combustão, as
partículas foram por certo arrastadas para a zona de transporte mas voltaram de novo ao leito.
Só assim, se pode explicar a grande contribuição, sobretudo das partículas de menor
dimensão, na transferência de calor para a água de arrefecimento.
Também o diâmetro da coluna pode afectar a taxa de elutriação. Lewis et al (1962),
verificaram por estudos feitos, que o arrasto das partículas era independente do diâmetro da
coluna para instalações com diâmetro maior que 0,1 m. Outros autores como Levenspiel
(1984) e Geldart (1998), fizeram estudos em colunas com diâmetro de 0,076 m e 0,152 m,
respectivamente, e verificaram que o arrasto das partículas era maior nas maiores unidades.
A velocidade superficial do gás tem uma influência óbvia na projecção de partículas,
tendo alguns autores, nomeadamente Choi et al (1998), verificado experimentalmente usando
areia que a taxa de elutriação era proporcional à velocidade elevada a uma potência que podia
variar entre 2 e 4.
A temperatura e pressão são também variáveis analisadas por diferentes autores.
Estudos de variação de pressão foram feitos por Chan and Knowlton (1984) que verificaram
um aumento linear do valor de TDH com a pressão e também um aumento da taxa de
elutriação. Para a análise da temperatura, Choi et al (1997) verificaram, no caso da areia, que
a taxa de elutriação atingia um mínimo entre 180 ºC e 430 ºC , aumentando de seguida. Estes
ensaios foram no entanto feitos em colunas de diâmetro 0,1 m e para velocidades superficiais
de 1,2 m/s, enquanto que no presente trabalho as temperaturas foram sempre superiores a
400 ºC, e a velocidade superficial variou entre 0,2 e 0,5 m/s.
Antes de proceder à determinação da correlação mais adequada, analisou-se a variação
de E0 com o excesso de gás, tendo em conta todos os ensaio efectuados com e sem
combustão. O resultado pode ser visualizado na figura seguinte,
185
9. Considerações sobre o comportamento do leito
1
E0 (kg/m2s)
0.8
0.6
0.4
0.2
0
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
v0-vmf (m/s)
107,5
142,5
180
282,5
357,5
107.5 comb
142,5 comb
180 comb
282,5 comb
357,5 comb
Figura 9.6 Fluxo de partículas versus excesso de gás para ensaios com e sem combustão, 113
observações.
Enquanto que para os ensaios sem combustão a gama de variação de v0-vmf é entre 0,15
e 0,4, uma vez que estes ensaios são feitos numa gama de temperaturas entre 400 e 700 ºC, os
ensaios com combustão são iniciados a 720 ºC, e portanto os valores de E0 obtidos
correspondem a uma faxa muito estreita de v0-vmf. No entanto, se compararmos os valores de
E0 para cada granulometria, considerando o mesmo excesso de gás, pode-se concluir que estes
são sempre superiores aos correspondentes no caso dos ensaios sem combustão. Isto seria de
esperar, uma vez, que nos ensaios com combustão o fluxo de sólidos deve ser incrementado
devido às explosões características destas reacções. Além disso, para as três menores
granulometrias ainda se verificou uma variação da pressão do leito durante o decorrer da
reacção de combustão, ou seja, houve transporte efectivo de partículas para fora do leito.
Nestes casos o fluxo de areia através da zona de transporte pode ser visto como a
contribuição de dois fluxos em paralelo. Segundo Wen-Ching (2003), um dos fluxos
corresponde ao fluxo contínuo de partículas desde o leito até à zona acima do TDH e, o outro,
corresponde ao espalhamento das partículas à superfície do leito devido ao excesso de gás que
sobe através do leito sob a forma de bolhas, partículas essas que depois caem para dentro do
leito.
Os valores experimentais obtidos do fluxo de partículas acima de TDH, para as três
granulometrias mais pequenas, foram determinados a partir dos declives dos gráficos da
186
9. Considerações sobre o comportamento do leito
variação da pressão no leito em função do tempo. No Capítulo 7 são apresentados alguns
destes gráficos correspondentes a ensaios típicos. Os valores experimentais, são apresentados
na tabela que se segue:
Tabela- 9.2 Valores experimentais médios de dp/dt para os vários caudais de ar e para diferentes
granulometrias.
mar(kg/h)
0,82
dp(µm)
1,0
1,2
dp/dt(cm/s)
107,5
0,002
0,004
.........
142,5
.......
0,003
......
180
......
0,002
0,004
Se estes valores forem convertidos em [kg/sm2] para que possam representar o fluxo de
sólidos, E∞, que vai até à zona acima de TDH, os resultados são os que aparecem na Tabela
9.3,
Tabela- 9.3 Valores experimentais de E∞, para os vários caudais de ar e para diferentes granulometrias
mar(kg/h)
0,82
1,0
1,2
E∞ (kg/sm2)
dp(µm)
107,5
0,02
0,04
.........
142,5
.......
0,03
......
180
......
0,02
0,04
Estes valores são muito pequenos quando comparados com os valores experimentais do
fluxo de sólidos total à superfície do leito E0, obtidos a partir da equação 9.4 e, por isso,
poderão incrementar muito pouco a taxa de transferência de calor para água devido à
convecção das partículas que são elutriadas para fora do leito. No entanto, estes valores
correspondem a uma variação da massa do leito de cerca de 25 a 30 %, durante a duração de
um ensaio, tendo em conta que a massa inicial do leito foi em média 0,33 kg e que a reacção
de combustão era mantida durante cerca de 1200 a 1500 s.
Vários modelos muito simples, são referidos na publicação de Wen-Ching (2003),
nomeadamente os apresentados por Pemberton and Davidson (1986) e por Wen and Chen
(1982) que permitem estimar o fluxo de partículas, E0 (kg/sm2), à superfície do leito. Todos
eles apresentam algumas variáveis comuns: diâmetro das partículas; excesso de gás (v0-vmf) e
187
9. Considerações sobre o comportamento do leito
diâmetro das bolhas. É com base nestas variáveis que se vai tentar arranjar um modelo que
melhor ajuste os dados experimentais.
O modelo proposto pode ser então do tipo
c
E0 = ad p b d BVS
(v0 − vmf ) d
(9.5)
Analisando a equação 2.2, usada para o cálculo do diâmetro das bolhas, dBVS, verifica-se
que essa equação pode ser escrita da forma seguinte:
dBVS α (v0-vmf)0,4
(9.6)
Então se for introduzida esta equação 9.6, na equação 9.5, o resultado obtido é o seguinte:
E0 = ad p b (v0 − vmf )c
(9.7)
sabendo o valor de ms obtido experimentalmente a partir da equação 9.3, o valor de E0 é
calculado a partir da equação 9.4 que se transcreve,
E0 =
ms
Aesc
(9.4)
Pela equação 9.7 verifica-se que o excesso de gás e o diâmetro das partículas são as
únicas variáveis envolvidas no cálculo do fluxo de sólidos à superfície do leito. Este resultado
é concordante com o que se previa, se for feita uma análise à variação da energia cinética do
gás. Repare-se que sendo o caudal de gás que passa sob a forma de bolhas proporcional a
(v0-vmf), então pode ser dado pela equação,
mg = ρ g ( v0 − vmf ) Aesc
Por outro lado a energia cinética do gás, Egc é,
188
(9.8)
9. Considerações sobre o comportamento do leito
E gc = mg
(v
0
−vmf
2
)
2
= ρ g ( v 0 −vmf ) Aesc
(v
0
−vmf
)
2
(9.9)
2
Como se verifica esta energia é proporcional a (v0-vmf)3.
Então, indo mais longe pode-se dizer que o fluxo de sólidos à superfície do leito, E0, é
proporcional à energia cinética do gás por unidade de massa das partículas. Tendo em atenção
a equação 9.9, o resultado que se obtém para estimar E0, pode ser escrito da forma,
E0 = α
ρ g ( v0 − vmf )
2 ρ pπ
3
(9.10)
d 3p
6
e simplificando esta equação 9.10, considerando que o quociente entre ρg/ρp se pode
considerar praticamente constante durante os vários ensaios, então chega-se à seguinte
equação,
E0 = α ´d p −3 (v0 − vmf )3
(9.11)
Comparando a equação 9.7 com a equação 9.11 verifica-se que o resultado é o mesmo
apenas são agora já conhecidos os parâmetros b e c que valem respectivamente -3 e 3. É com
base nesta última equação, que se vai procurar uma correlação que ajuste o melhor possível os
resultados experimentais obtidos de E0, recorrendo mais uma vez ao programa de optimização
NLREG para o cálculo do parâmetro α´.
O resultado obtido foi o seguinte,
E0m = 2, 98 ×10 −11 d p−3 ( v0 − vmf
)
3
(9.12)
em que todas as variáveis são introduzidas no Sistema Internacional de unidades.
Os limites de aplicabilidade desta correlação são:
- 107,5 < dp(µm) < 357,5
- 400 < TL(ºC) < 836
- 1,0 < mar(kg/h) < 1,5
189
9. Considerações sobre o comportamento do leito
No entanto, o desvio médio obtido foi de Dm=64% que é um valor muito elevado e que
já seria de prever face aos resultados apresentados na Figura 9.6. Este valor do Dm é devido
essencialmente às grandes diferenças existentes entre valores experimentais e calculados pelo
modelo, no caso de todos os ensaios com combustão e no caso das duas maiores
granulometrias para ensaios sem combustão. Isto pode ser visualizado nas figuras seguintes,
onde se apresentam os valores de E0m, previstos por este modelo em função de v0-vmf, bem
como os valores experimentais E0, que estiveram na base do referido modelo. A Figura 9.7
refere-se aos ensaios sem combustão, e a Figura 9.8 aos ensaios com combustão.
1
2
E0 e E0 (kg/m s)
0.8
m
0.6
0.4
0.2
0
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
vo-vmf (m/s)
107,5
142,5
180
282,5
357,5
107,5
142.5
180
282,5
357,5
Figura 9.7 Fluxo de partículas experimental e previsto pelo modelo nos ensaios sem combustão.
O modelo proposto parece convincente para as três menores granulometrias, mas
conduz a grandes desvios quando aplicado às duas maiores granulometrias, sendo os valores
experimentais nestes casos sempre superiores aos previstos pelo modelo. Isto significa, que os
valores experimentais calculados pela equação 9.4 são valores excessivos dado o pequeno
grau de borbulhamento que existe nestes leitos. Uma das causas que pode conduzir a estes
valores excessivos é o valor experimental da potência térmica atribuída às partículas. Como
nestes casos esse calor é mais pequeno, então o peso do calor axial que foi menosprezado
desde o início deste trabalho, pode ter agora nesta análise um peso relevante. Desta maneira
essa quantidade de calor que está a ser imputada às partículas devido ao seu movimento, é por
si um valor excessivo. Uma outra causa pode ser também o valor atribuído à temperatura da
parede que foi um valor estimado e não adquirido experimentalmente.
190
9. Considerações sobre o comportamento do leito
Apresenta-se de seguida a Figura 9.8 equivalente à Figura 9.7 mas para os ensaios com
combustão,
1
E0 e E0m (kg/m2s)
0.8
0.6
0.4
0.2
0
0.1
0.12
0.14
0.16
0.18
0.2
v0-vmf (m/s)
0.22
0.24
0.26
0.28
107,5
142,5
180
282,5
357,5
107,5
142,5
180
282,5
357,5
Figura 9.8 Fluxo de partículas experimental e previsto pelo modelo nos ensaios com combustão.
Neste caso, é evidente a grande diferença encontrada entre o modelo proposto e os
valores experimentais. Como se pode constatar, os desvios são muito grandes o que permite
concluir que o modelo não prevê o fluxo de partículas que ocorre devido às explosões
decorrentes da reacção de combustão.
São todos estes ensaios, e os correspondentes às duas maiores granulometrias no caso de
dos ensaios sem combustão, que contribuíram para o desvio médio de 64% que se obteve.
O raciocínio inerente ao modelo proposto aparenta ser exacto quando aplicado às três
dimensões menores de partículas no caso de não existir reacção de combustão. Como são
estas partículas, as que terão mais interesse para desenvolvimento de trabalhos futuros,
nomeadamente no que diz respeito à circulação de sólidos, determinou-se a partir do mesmo
modelo, um novo valor de α´ considerando apenas estas últimas partículas e os ensaios sem
combustão.
O resultado foi o seguinte,
E0m = 2, 65 × 10−11 d p−3 ( v0 − vmf
)
3
(9.13)
em que todas as variáveis são mais uma vez introduzidas no Sistema Internacional de
unidades.
191
9. Considerações sobre o comportamento do leito
Os limites de aplicabilidade desta correlação são:
- 107,5 < dp(µm) < 180
- 400 < TL(ºC) < 730
- 1,0 < mar(kg/h) < 1,5
Neste caso o Dm = 30 %, e o resultado pode ser visto na Figura 9.9
1
2
E0 e E0 (kg/m s)
0.8
m
0.6
0.4
0.2
0
0.15
0.2
0.25
0.3
0.35
0.4
v0-vmf (m/s)
107,5 exp
107,5
142,5 exp
142,5
180 exp
180
Figura 9.9 Fluxo de partículas versus excesso de gás para as três menores dimensões e para os ensaios
sem combustão.
192
10. Conclusões e propostas de trabalho futuro
10.Conclusões e propostas de trabalho futuro
O estudo da transferência de calor da superfície livre de um leito borbulhante fluidizado
para um permutador de parede de membrana foi conduzido em duas fases:
- 1ª fase- a fluidização foi conseguida apenas com ar à pressão atmosférica e usadas
temperaturas do leito que variaram entre 400 ºC e 700 ºC.
- 2ª fase- usou-se uma mistura rica (defeito de ar) de ar e propano comercial a 91%
provocando-se a auto-ignição do propano à temperatura de 720 ºC e à pressão atmosférica.
Para este estudo foram utilizadas 5 granulometrias diferentes de areia de sílica, com
diâmetros médios expressos em µm, de 107,5; 142,5; 180; 282,5 e 357,5. O caudal de ar
usado, para ambas as fases do trabalho, situou-se entre 0,85 kg/h e 1 kg/h, variando a
velocidade superficial do ar, às várias temperaturas do leito, entre 0,2 e 0,5 m/s. Esta gama de
trabalho conduziu a um escoamento laminar do gás dentro da coluna, variando o valor do
número de Reynolds entre 200 e 400. O aquecimento do ar foi feito com uma resistência
eléctrica de 2000 W de potência e, para que se atingisse a temperatura necessária à autoignição do propano foi necessário manter a pressão do leito entre 10 a 15 cm de água. Para
pressões maiores que 15 cm não se conseguiam atingir no leito condições de estado
estacionário correspondentes às condições mínimas de temperatura necessárias à auto-ignição
do propano, o que provou que a potência eléctrica da resistência não era suficiente face às
dimensões da instalação e às características físicas dos sólidos usados. O caudal de água que
circulou na camisa variou entre 35 a 140 kg/h, o que também conduziu a um escoamento
laminar nesta zona da coluna. No caso dos ensaios de combustão usaram-se caudais
depropano entre 0,1 e 0,12 kg/h o que permitiu trabalhar em condições de mistura rica, com
valores de riqueza da mistura r entre 1,6 e 1,8.
Uma das primeiras constatações comum a todos os ensaios realizados foi o facto do
caudal de água não influenciar a taxa de transferência de calor. Isto foi comprovado pela
193
10. Conclusões e propostas de trabalho futuro
determinação dos valores de he obtidos por correlações empíricas adequadas a escoamento
laminar em espaços anelares. Esses valores, situaram-se entre 230 e 380 W/m2K que são
muito maiores do que os obtidos para o lado interno do permutador, o que torna a resistência
daquele lado desprezável. A outra resistência desprezada foi a resistência de condução através
da parede interna do permutador, uma vez que o seu valor é de 4,31x10-4 K/W. Face a estes
resultados e conclusões, foi possível estimar a temperatura da parede interior do permutador
e, esta, foi considerada constante em cada ensaio, para posterior tratamento de dados.
Foi também feita a correcção das temperaturas lidas pelos termopares, fazendo um
balanço de energia entre a troca de calor por radiação destes com a parede e, a transferência
de calor por convecção, dos mesmos com o gás. Esta correcção é necessária sempre que os
termopares estão inseridos numa conduta pequena, em que a temperatura da parede é muito
inferior à do gás.
Depois destas constatações gerais, vai ser feita uma sistematização das conclusões a que
se chegou, sendo esta apresentada de acordo com as duas fases referidas neste trabalho.
10.1 Análise dos resultados na ausência de combustão
Verificou-se em todos os ensaios que a variação da entalpia da água foi sempre superior
à variação da entalpia do ar. Se forem analisadas, por exemplo as Figuras 4.1, 4.2 e 4.3
relativas a ensaios feitos a 700 ºC, PL =10 cm e mar =1 kg/h, verifica-se que essa diferença é
independente do caudal de água que circula na camisa e corresponde a cerca de 300 W. Para
tentar explicar esta diferença analisou-se a componente axial ao longo da parede interna do
permutador. Por ensaios feitos com corte de ar depois de atingidas condições de estado
estacionário, verificou-se que essa componente era insignificante e desprezou-se para efeitos
de cálculo, pois o seu valor variou entre 25 e 100 W que corresponde a um acréscimo da
temperatura da água, na gama dos caudais de trabalho, de apenas 0,5 a 1 ºC.
Passou-se então, ao estudo dos mecanismos de transferência de calor envolvidos neste
processo de transferência de calor entre a superfície de um leito borbulhante e um permutador
de parede de membrana, não esquecendo a análise da hidrodinâmica do leito, face aos caudais
de ar e às características das partículas.
A potência térmica recebida pela água depende de várias contribuições:
- convecção do gás para a parede interna do permutador;
- radiação entre o leito e a parede e participação dos gases quando há combustão;
194
10. Conclusões e propostas de trabalho futuro
- convecção devido ao espalhamento das partículas a partir da superfície do leito.
A determinação da componente devido à convecção do gás foi determinada
experimentalmente através da variação da entalpia do gás. Verificou-se que o aumento, quer
da temperatura do leito quer do caudal de ar, embora se traduzisse, como seria de esperar,
num aumento da potência térmica do ar, esse aumento foi pequeno, sobretudo quando
comparado com o incremento que acarretou na variação da entalpia da água. Isto significa que
o fenómeno da convecção não é o mais importante no aquecimento da água. Além disso,
verificou-se que para as mesmas condições de operação, foram as partículas de dp=107,5 µm e
dp= 142,5 µm que permitiram um aumento maior no calor recebido pela água. Para as outras
três granulometrias mesmo conseguindo trabalhar com caudais mais altos de gás às
temperaturas mais elevadas, o incremento verificado na temperatura da água não se tornou tão
evidente. Isto mais uma vez vem dar ênfase à pouca importância da convecção.
Quanto à determinação do calor transferido por radiação do leito para a parede do
permutador, esta teve que ser feita recorrendo a um modelo teórico. Esse modelo conduziu a
valores de hradL entre 0,5 e 1,2 W/m2K, independentemente da granulometria da areia e do
caudal de gás, o que mostra também a pouca influência da radiação no aquecimento da água.
Por fim, foi então analisada a componente devido à convecção das partículas desde a
superfície do leito até à zona de transporte. Para isso foi preciso analisar a hidrodinâmica dos
vários tipos de leitos.
Para qualquer dimensão de partículas as condições operatórias corresponderam sempre a
leitos borbulhantes, uma vez que a determinação de Rec, que permite analisar a transição de
regime borbulhante para turbulento, conduziu sempre a valores superiores aos de Rep. No
entanto, face ao diferente comportamento observado para as diferentes granulometrias, no que
diz respeito à taxa de transferência de calor para água, foi feita uma análise mais detalhada do
grau de borbulhamento atingido por cada dimensão face às mesmas condições operatórias. Os
valores de v0/vmf variaram entre um máximo de 40 para as partículas com dp=107,5 µm e um
mínimo de 2 para as partículas de dp =357,5 µm. Esta grande diferença no grau de
borbulhamento vai influenciar o fluxo de partículas que é projectado a partir da superfície do
leito devido às bolhas que rebentam à superfície. Quanto maior é o diâmetro das partículas,
menor é o fluxo de partículas projectado para a zona do permutador e como se verifica
experimentalmente, menor é a diferença existente entre a variação da entalpia da água e do ar,
como aliás já foi referido. Isto vem comprovar que o fenómeno de borbulhamento, que
195
10. Conclusões e propostas de trabalho futuro
conduz ao espalhamento das partículas é o fenómeno que mais influência tem no aquecimento
da água.
No Capítulo 9 comprovou-se através das correlações encontrados para a determinação
do fluxo de partículas à superfície do leito, que esse fluxo é maior quanto menor for a
dimensão das partículas. No entanto, as correlações propostas só se adaptaram bem às três
menores granulometrias nos ensaios sem combustão, havendo dificuldade em assegurar um
ajuste adequado para as duas maiores granulometrias. Os valores experimentais de E0 são
sempre muito superiores aos previstos pela correlação, o que permite concluir que o termo
correspondente às explosões não está a ser devidamente contabilizado e é uma parcela muito
importante relativamente à contribuição das partículas na transferência de calor.
Determinou-se também uma correlação para cálculo de hpct tendo em consideração todos
os ensaios feitos, com e sem combustão, obtendo-se nesse caso um Dm = 29%.
Como um dos objectivos deste trabalho era a determinação de uma correlação
apropriada para o cálculo hglo apresenta-se aqui a equação encontrada,
Nucalc
 v
= 14, 7 Re −0,35 Pr  0
 vmf




−0,09
 dp 
 
 di 
−0,47
  T −T
w
 ln  L corr
  TL − Tgs
 

 


0,21
(5.17)
Válida dentro dos seguintes limites:
- 107,5 < dp (µm) < 357,5
- 400 < TL (ºC) < 700
- 200 < Rear < 400
- 2 < v0/vmf < 40
10.2 Análise dos resultados com combustão
Para poder analisar a influência da granulometria do leito, na evolução da reacção de
combustão de propano, e comparar então a taxa de transferência de calor para a água, era
necessário que as condições de arranque de combustão fossem o mais próximas possíveis. No
entanto, face à constatação do diferente comportamento das várias granulometrias, foi
necessário que o arranque da combustão para as partículas de dp=107,5 µm, se fizesse ao
196
10. Conclusões e propostas de trabalho futuro
caudal de ar de 0,82 kg/h, pois só assim era possível atingir neste leito a temperatura de
720 ºC.
Nos ensaios com combustão há três fenómenos muito importantes que se devem
analisar:
- Como já foi referido o grau de borbulhamento do leito diminui quando o diâmetro das
partículas aumenta, e esse facto influencia, tal como nos ensaios sem combustão, a taxa de
transferência de calor para a água, devido à convecção das partículas. No entanto, o
movimento das partículas é aqui acentuado devido às explosões que ocorrem resultantes da
reacção de combustão.
- A zona de chama onde se processa a reacção, no interior ou mais à superfície do leito,
que pode ser avaliada a partir da evolução das temperaturas do lado dos gases.
- A variação da pressão do leito que foi constatada para as três menores dimensões,
apenas nos ensaios com combustão, e que permite concluir que houve uma percentagem de
partículas que além de entrar na zona de transporte saiu da coluna arrastada pela corrente de
gás.
No caso das duas menores dimensões de partículas, a reacção manteve-se à superfície do
leito, houve um aumento grande na variação da entalpia da água sem contudo se notar grande
variação da entalpia do gás relativamente às condições de ausência de combustão. Neste caso,
a influência do grau de borbulhamento é atenuada pela presença da chama que incrementa a
parcela correspondente à radiação. A variação de pressão no entanto não influencia a taxa de
transferência de calor, uma vez que o fluxo de sólidos que foi elutriado é praticamente
desprezável relativamente ao espalhamento de partículas à superfície do leito.
As partículas de dp=180 µm apresentaram um comportamento semelhante ao anterior,
contudo, não provocaram um aumento tão acentuado na variação da entalpia da água para os
mesmos caudais de ar e, nesses casos, verificou-se que a reacção se mantinha dentro do leito.
Para caudais de ar mais elevados a reacção teve tendência a evoluir para a superfície do leito.
No caso de dp =282,5 µm e dp =357,5 µm o comportamento entre as duas granulometrias
foi semelhante mas muito diferente do demonstrado pelas outras partículas. Neste caso houve
um aumento brusco da temperatura do leito e uma descida acentuada da temperatura dos
gases à entrada do permutador. Isto significou que a reacção se processou no interior do
próprio leito, sendo difícil a estabilização da chama e também atingir na água, condições de
estado pseudo estacionário. A partir de um certo tempo a chama avança para a zona de
transporte mas a reacção extingue-se devido às temperaturas baixas dessa zona. Como o grau
de borbulhamento é, no caso destas partículas, muito mais baixo, não há variação da pressão
197
10. Conclusões e propostas de trabalho futuro
do leito e a chama mantém-se dentro do leito nesta fase de reacção. Verifica-se então, que a
variação da entalpia da água é neste caso menos acentuada e a variação da entalpia do gás é
da mesma ordem de grandeza das outras partículas e dos ensaios sem combustão.
Como conclusão final verificou-se que para a mesma fase da reacção há uma diminuição
do calor recebido pela água com o aumento do diâmetro das partículas, o que pode ser
comprovado pela análise das Figuras 7.27 e 7.28.
Também para estes ensaios se determinou uma correlação empírica que envolveu os
mesmos grupos adimensionais da equação 5.17, mas foi acrescentado a variável r, riqueza da
mistura. A correlação encontrada foi:
Nucal
 v
= 2, 25 Re0,103 Pr  0

 vmf



−0,094
 dp 
 
 di 
−0,38
  T −T
W
 ln  L corr
  TL − Tgs
 

 


0,078
r 0,18
(7.2)
Válida para as seguintes condições:
- 107,5 < dp (µm) < 357,5
- 0,85 < mar (kg/h) < 1,2
- 0,09< mpro (kg/h) < 0,12
- 1,4 < r < 1,9
- 257 < Re < 357
- 700 < TL(ºC) < 836
10.3 Resultados com e sem combustão
Embora seja discutível a comparação dos resultados obtidos com e sem combustão, já
que as condições e trabalho foram diferentes e em cada fase se pretenderam analisar
parâmetros também diferentes, foi determinada uma correlação geral a partir de todos os
ensaios feitos considerando no caso da combustão, os pontos experimentais correspondentes à
mesma fase de reacção
A correlação encontrada foi,
Nucal = 17, 3Re
198
−0,24
 v
Pr  0
 vmf




−0,024
 dp 
 
 di 
−0,30
  T −T
W
 ln  L corr
  TL − Tgs
 

 


0,17
r 0,78
(8.1)
10. Conclusões e propostas de trabalho futuro
Esta correlação é válida dentro dos seguintes limites:
- 107,5 < dp (µm) < 357,5
- 0,85 < mar (kg/h) < 1,2
- 0,09< mpro (kg/h) < 0,12
- 1,4 < r < 1,9; r =1 para ausência de combustão
- 200 < Re < 400
- 400 < TL (ºC) < 836
10.4 Propostas de trabalho futuro
Face aos problemas que se foram detectando no decorrer do trabalho experimental e
com a intenção de melhorar e complementar o estudo aqui realizado, propõem-se as seguintes
alternativas para trabalho futuro:
- Trabalhar com caudais de ar e consequentemente de propano numa gama mais
alargada, para que seja possível, quer nos ensaios sem combustão, quer nos realizados na
presença do propano, tornar mais universais as correlações encontradas. Para isso torna-se
necessário dispor de uma resistência de aquecimento mais potente apesar dos perigos que isso
possa acarretar. Pode-se também pensar em fazer um pré-aquecimento do ar antes deste ser
alimentado à coluna.
- Para que não existam riscos de pré ignição do propano antes do leito, sobretudo se for
feito o pré-aquecimento do ar, é também aconselhável fazer a alimentação do ar e do propano
em estágios diferentes da coluna. Também se pode pensar em admitir o caudal de ar em dois
níveis diferentes da coluna, tendo assim uma entrada correspondente ao ar primário e uma
outra ao ar secundário.
- Usar outro tipo de material inerte, para estudar a influência da densidade da suspensão
na transferência de calor no caso de leitos borbulhantes para permutadores de parede de
membrana. Ao usar materiais menos densos pode-se conseguir trabalhar em condições de
leito turbulento e até circulante e comparar os diferentes escoamentos relativamente à
transferência de calor.
199
10. Conclusões e propostas de trabalho futuro
- Tentar arranjar uma metodologia experimental de modo a que se possa quantificar com
exactidão os caudais de partículas projectadas para fora do leito e que caem novamente, para
tentar validar e complementar a correlação que foi obtida neste trabalho.
- No caso de se conseguir trabalhar com leitos turbulentos ou circulantes é necessário
aquecer o braço descendente da coluna a seguir ao ciclone e mantê-lo isolado, para que as
partículas possam voltar ao leito quentes sem provocarem o arrefecimento do leito. Só assim
será possível manter condições de estado estacionário no leito.
- Usar na construção do reactor, se possível na zona do leito, materiais que resistam a
altas temperaturas e que permitam visualizar os fenómenos de borbulhamento e espalhamento
de partículas que aí se verificam.
- Usar analisadores para poder determinar com rigor a extensão da reacção de
combustão e assim analisar a sua influência na taxa de transferência de calor.
- Usar metodologias que permitam uma quantificação adequada da importância da
radiação com gases participantes no caso de ensaios com combustão.
- Introduzir técnicas de medição da temperatura na parede interna ao longo do
permutador.
200
11.Bibliografia
11.Bibliografia
Al-Busoul, A., 2002, “Bed-to-Surface Heat Transfer in a Circulating Fluidized Bed”, Heat
and Mass Transfer, 38, pp.295-299.
Bai, D., Kato, K.,1999, “Quantitative Estimation of Solids Holdups at Dense and Dilute
Regions of Circulating Fluidized Beds”, Powder Technology, 101, pp.183-190.
Basu, P., Nag P.K., 1987, “An Investigation into Heat Transfer in Circulating Fluidized Beds”
International Journal of Heat and Mass Transfer, 30, pp.2399-2409.
Basu, P., Nag P.K., 1996, ”Heat Transfer To Walls of a Circulating Fluidized Bed Furnace”,
Review Article Number 48, Chemical Engineering Science, Vol 51, (1), pp. 1-26.
Behzadmehr, A., Galanis N., Laneville A., 2003, “Low Reynolds number mixed convection
in vertical tubes with uniform wall heat flux”, International Journal of Heat and Mass
Transfer, Pergamon, pp. 4823-4833.
Bi, H.T., Grace J.R., et al, 2000, “A state of–the–art review of gas–solid turbulent
fluidization”, Chemical Engineering Science, 55, pp. 4789-4825.
Bird, R.B., Stewart W.E. e Lightfoot E.N.,1960, ”Transport Phenomena”, John Wiley and
sons, New York.
Breitholtz, C., Leckner B., 2000a, “Translation of Heat Transfer Measurements from
Laboratory CFBs to the conditions of CFB-boilers”, 4th Minsk International Heat and Mass
Transfer Forum, Minsk.
201
11.Bibliografia
Breitholtz, C., Leckner B., 2000b, “Wall Average Heat Transfer in CFB – Boilers”, 3th
European Conference on Fluidization, Toulouse, France.
Breitholtz, C., Leckner B., 1997, ” Heat Transfer in Circulating Fluidized Bed Boilers- do we
know sufficiently?”, Trends in Heat, Mass & Momentum Transfer, 3, pp.85-104.
Çengel, Y. A., 1998, “Heat Transfer”, 1ª Edição, McGraw-Hill.
Çengel, Y. A., 2003, “Heat Transfer”, 3ª Edição, McGraw-Hill.
Churchill, S. W., 1976, “A comprehensive correlating equation for laminar, assisting forced
and free convection”, AIChe Journal, 23, (1), pp. 10-16.
Coulson, J. M., Richardson J.F., 1965, “Tecnologia Química” Vol. I., 2ª Edição, Fundação
Calouste Gulbenkian.
Dounit, S., Hemati M., Steinmetz D., 2001, “Natural gas combustion in fluidised bed reactors
between 600 and 850 ºC: experimental study and modelling of the freeboard”, Powder
Technology 120, pp.49-54.
EEA Report, European Environment Agency 2006, No 7, “How much bioenergy can Europe
produce without harming the environment?”
Gayan, P.et al, 2004, “Circulating fluidised bed co-combustion of coal and biomass”, Fuel,
83, pp.277-286.
Geldart, D., 1986, “Gas fluidization technology”, John Wiley and Sons, New York.
Gupta, S. K., Berruti, F., 2000, “Evaluation of the Gas-Solid Suspension Density in CFB
Risers with Exit Effects”, Powder Technology, 108, pp. 21-31.
Howell, J. R., Buckius, R., O., 1984, “Fundamentals of Engineering Thermodynamics”,
McGraw-Hill Book Company.
Incropera, Frank P., Witt David P., 1990, “Fundamentos de transferência de calor e massa“,3ª
Edição, Guanabara Koogan.
202
11.Bibliografia
Johnsson, F., 2000, ”Hydrodynamic Modelling of Circulating Fuidized Bed Risers”, Mid term
status of task 1.1 (project JOR3CT980306), pp. 2-51.
Johnsson, H., Johnsson, F., 2001, “Measurements of Local Solids Volume-Fraction in
Fluidized Bed Boilers”, Powder Technology, 115, pp.13-26.
Kaferstein, P., Tepper H., 1997, “Fluidization, Combustion and Emission Behavior of
Biomass in Fluidized Bed Combustion Units”, ASME, Vol 1, Fluidized Bed Combustion.
Kunii, D., Levenspiel, O., 1991, “Fluidization Engineering”, 2ª Edição, Butterworth.
Kuzman, Raznjevic, 1970, “Tables et Diagrammes termodynamiques”,Editions Eyrolles.
Liang-Shih, F., Chao Zhu, 1998, “Principles of Gas-Solid Flows”, Cambridge University
Press.
Marcus, R.D., Leung, L.S., Klinzing G.E., Rizk, F., 1990, “Pneumatic Conveying of solids”,
Chapman and Hall, London.
McIntyre, A.J., 1988, “Ventilação Industrial e controle de poluição”, Editora Guanabara , Rio
de Janeiro.
Molerus, O., Burschka A., 1995, “Particle migration at solid surfaces and heat transfer in
Bubbling fluidized beds- I. Particle migration measurement systems”, Chemical Engineering
Science, Vol.50, (5), pp. 871-877.
Molerus, O., Burschka A., 1995, “Particle migration at solid surfaces and heat transfer in
Bubbling fluidized beds- II. Prediction of heat transfer in bubbling fluidized beds”, Chemical
Engineering Science, Vol.50, (5), pp. 879-885.
Noymer, P.D., Glicksman L.R., 1998 “ Cluster Motion and Particle Convective Heat Transfer
at the Wall of a Circulating Fluidized Bed”, International Journal of Heat and Mass Transfer,
41, (1); pp.147-158.
Obenberger, I., 1998, “Decentralized biomass combustion state of the art and future
development”, Biomass and Energy, Vol 15, (1), pp. 33-56.
203
11.Bibliografia
Ozisik, M. Necati, 1985, “Transferência de calor- um texto básico”, Guanabara.
Pagliuso, J.D., Lombardi G., 2000, “Experiments on the Local Heat Transfer Characteristics
of a Circulating Fluidized Bed”, Experimental Thermal and Fluid Science, 20, pp.170-179.
Pinho, C., 2005, “Combustão”, Departamento de Engenharia Mecânica e Gestão Industrial,
F.E.U.P..
Rhodes, M., 1996, “What is turbulent fluidization”, Powder Technology, Elsevier, 88,
pp. 3-14.
Rhodes, M., 1998, “Introduction of Particle Technology”, John Wiley & Sons, Monash
University, Austrália.
Rhodes, M.J., Geldart D., 1989, “The Upward Flow of Gas/Solid Suspensions; Part1: A
Model for the Circulating Fluidized Bed Incorporating Dual Level Gas Entry into the Riser”,
Chem. Eng. Res. Des., 67, pp.20-29.
Ribeiro, L.J.S., 2002, “Combustão de propano em leitos fluidizados de areia “, Tese de
Doutoramento em Engenharia Mecânica, F.E.U.P.
Ribeiro, L. and Pinho, C., 2004 “Generic Behaviour of propane combustion in fluidized
beds”, Chemical Engineering Research and Design, 82(A12), pp.1597-1603.
Rizk, F., 1986, “Chapter 10 - Principles of Pneumatic Conveying. Encyclopedia of Fluid
Mechanics. Volume 4. Solids and Gas Solids Flows”, N.P.,Cheremisinoff, Editor. Gulf
Publishing Company.
Subbarao, D., Basu, P., 1986, “A Model for Heat Transfer in Circulating Fluidized Beds”,
International Journal of Heat and Mass Transfer, 29, (3), pp.487-489.
Sundaresan, R., Kolar, A.K., 2002, “Core Heat Transfer Studies in a Circulating Fluidized
Bed”, Powder Technology, 124, pp.138-151.
Vardeman, Stephen B., 1994, “Statistics for Engineering Problem solving”, Boston, PWS
Publishing Company.
204
11.Bibliografia
Wang, X.S., Gibbs, B.M., Rhodes M., 1995, “Flow Structure in a CFB Riser-Effect of
Operating Temperature”, Fluidized Bed Combustion, ASME, 1, pp. 663-670.
Wen, C.Y., Chen, L.H., 1982, “Fluidized Bed Freeboard Phenomena: Entrainment and
Elutriation”, AIChE Journal, Vol 28, (1), pp. 117-128.
Wen-Ching, Y., 2003, “Handbook of Fluidization and Fluid- Particle Systems”, Marcel
Dekker,Inc, NewYork. Basel.
White, Frank M., 1991,”Viscous Fluid Flow”, 3ª Edição, McGraw-Hill.
William, H. McAdams, 1954, “Heat Transmission”, 3ª Edição, McGraw-Hill.
Wirth, K.-E., 1995, “Heat Transfer in Circulating Fluidized Bed”, Chemical Engineering
Science, 50, (13), pp. 2137- 2151.
Wu, R.L., Lim, C.J., Grace, J.R. 1987, “Heat Transfer from a circulating Fluidized Bed to
Membrane Waterwall Surfaces”, AIChE Journal, 33, (11), pp. 1888-1893.
Wu, R.L., Lim, C.J., Grace, J.R.,1989, ”Suspension-to-Surface Heat Transfer in a CirculatingFluidized- Bed Combustor”, AIChE Journal, 35, (10), pp. 1685-1691.
205
Apêndice I - Caracterização da areia
Apêndice I. Caracterização da areia
De acordo com o procedimento experimental referido no Capítulo 3, no que diz respeito
à caracterização das várias granulometrias de areia, apresentam-se neste apêndice os
resultados obtidos para as várias partículas usadas.
São também aqui apresentadas as equações e os gráficos correspondentes à variação da
velocidade mínima de fluidização e à variação da velocidade terminal, em função da
temperatura, para todas as granulometrias com que se trabalhou.
A.I.1 Características das partículas
A tabela que se segue apresenta os resultados finais relativamente às propriedases físicas
obtidas para as diferentes granulometrias de areia usadas no decorrer deste trabalho.
Tabela A.I.1- Características das partículas de areia
dp
ρp
ρL
εmf
(µ
µm)
(kg/m )
(kg/m3)
107,5
2506
1230
0,46
142,5
2560
1290
0,48
180
2590
1280
0,42
282,5
2631
1430
0,45
357,5
2627
1480
0,44
3
207
Apêndice I - Caracterização da areia
A.I.2 Velocidade mínima de fluidização e velocidade terminal de uma partícula em
função da temperatura
A determinação da velocidade mínima de fluidização foi feita através da equação de
Ergun apresentada por Kunii e Levenspiel (1991) e considerando como aproximação o factor
de esfericidade igual a um para todas as granulometrias.
O processo de cálculo para a velocidade mínima de fluidização foi então o seguinte:
Determinação de Remf pela equação de Ergun
1, 75
ε
3
mf
2
Remf
+
150(1 − ε mf )
ε mf3
Re mf = Ar
(A.I.1)
em que;
Re mf =
Ar =
ρ g vmf d p
µg
(A.I.2)
d 3p ρ g ( ρ p − ρ g ) g
(A.I.3)
µ g2
A velocidade terminal das partículas foi determinada pela equação obtida através de um
balanço de forças feito a uma partícula tal como apresentado por Kunii e Levenspiel (1991).A
equação resultante desse balanço é a seguinte:
 4d p ( ρ p − ρ g ) g 
v t= 


3ρ g C D


0.5
(A.I.4)
em que o coeficiente de arrasto pode ser determinado pela equação desenvolvida por Kaskas
em 1964 referida em Marcus (1990) e válida para todos os regimes de escoamento
CD =
em que
208
Re p =
24
4
+
+ 0, 4
Re p
Re p
(A.I.5)
ρ g vt d p
µg
(A.I.6)
Apêndice I - Caracterização da areia
As correlações determinadas para cálculo de vmf = f(T) e de vt = f(T) envolvem ambas
processos iterativos. Além disso é preciso estimar as propriedades do ar em função da
temperatura de operação.
Para o cálculo da massa volúmica do ar, ρar admite-se comportamento de gás perfeito
ρ ar =
P × M ar
RT
(A.I.7)
Para o cálculo da viscosidade, µg, usa-se a correlação proposta por White (1991)
 T 
µ g = 1, 716 ×10 

 273 
−5
3/ 2
273 + 111
T + 111
(A.I.8)
válida para 170 <T[K]< 1900
Para as partículas com dp=180 µm os resultados obtidos para cálculo de vmf em função
da temperatura encontram-se na tabela abaixo. Para todas as outras granulometrias apenas se
apresentam os resultados sob a forma de figuras com as respectivas correlações. São todas
estas correlações, que são introduzidas no sistema de aquisição de dados antes dos ensaios
feitos com a respectiva granulometria.
Tabela A.I.2 Resultados obtidos para determinação de vmf = f(T) usando a equação A.I.1 para as
partículas de dp=180 µm
T(ºC)
ρar
µar
3
Ar
Remf
Equação
(εmf=0,42)
A.I.1
Balanço
vmf
(m/s)
(kg/m )
(Pa.s)
200
0,735
2,57x10-5
164,12
0,139
164,12
-4,91x10-5
0,0271
300
0,606
2,93x10-5
104,56
0,089
104,56
-1,28x10-5
0,0239
400
0,516
3,25 x10-5
72,19
0,061
72,19
-4,24x10-6
0,0215
0,450
3,55 x10
-5
52,74
-1,66x10
-6
0,0197
-5
40,17
0,034
40,.17
-7,34x10
-7
0,0183
500
52,74
0,045
600
0,398
3,83 x10
700
0,357
4,09 x10-5
31,60
0,027
31,60
-3,57x10-7
0,0171
800
0,324
4,34 x10-5
25,49
0,022
25,49
-1,88x10-7
0,0161
900
0,296
4,57 x10-5
20,99
0,018
20,99
-1,05x10-7
0,0153
950
0,284
4,68 x10-5
19,17
0,016
19,17
9,20x10-4
0,0149
209
Apêndice I - Caracterização da areia
Para a mesma granulometria, os resultados obtidos para a determinação de velocidade
terminal em função da temperatura encontram-se também na tabela abaixo:
Tabela A.I.3 Resultados obtidos para determinação de vt = f(T) usando a equação A.I.4 e A.I.5 para as
partículas de dp=180 µm
ρar
T(ºC)
µar
3
(kg/m )
Ar
(Pa.s)
vt
(m/s)
CD
Balanço
200
0,735
2,57X10-5 164,12
1,17
6,00
-2,47x10-4
300
0,606
2,93X10-5 104,56
1,11
8,18
-1,64x10-5
400
0,516
3,25X10-5
72,19
1,05
10,72
-5,58x10-5
500
0,450
3,55X10-5
52,74
1,00
13,61
-1,01x10-4
600
0,398
3,83X10-5
40,17
0,95
16,87
-1,46x10-4
700
0,357
4,09X10-5
31,60
0,91
20,48
-1,85x10-4
800
0,324
4,34X10-5
25,49
0,88
24,44
-2,20x10-4
900
0,296
4,57X10-5
20,99
0,85
28,77
-2,50x10-4
950
0,284
4,68X10-5
19,17
0,83
31,07
-2.63x10-4
Os gráficos correspondentes aos resultados apresentados nas Tabelas A.I.2 e A.I.3 são
respectivamente
3.00E-02
2.50E-02
vmf (m/s)
2.00E-02
1.50E-02
y = -2.11E-11x 3 + 5.38E-08x 2 - 5.42E-05x + 3.59E-02
R2 = 1.00E+00
1.00E-02
5.00E-03
0.00E+00
0
200
400
600
800
T(ºC)
Figura A.I.1- vmf = f(T) para dp=180 µm
210
1000
Apêndice I - Caracterização da areia
1.40
1.20
vt (m/s)
1.00
0.80
0.60
y = 1.2669e-0.0005x
R2 = 0.9933
0.40
0.20
0.00
0
200
400
600
800
1000
T(ºC)
Figura A.I.2- vt = f(T) para dp=180 µm
As figuras que se seguem são apresentadas por ordem crescente de granulometria:
1.40E-02
1.20E-02
8.00E-03
6.00E-03
y = -1.04E-11x3 + 2.65E-08x2 - 2.66E-05x + 1.76E-02
R2 = 1.00E+00
4.00E-03
2.00E-03
0.00E+00
0
200
400
600
800
1000
T(ºC)
Figura A.I.3- vmf = f(T) para dp=107.5µm
0.60
0.50
0.40
vt (m/s)
vmf (m/s)
1.00E-02
0.30
0.20
y = 2.5831x-0.3058
R2 = 0.9917
0.10
0.00
0
200
400
600
800
1000
T(ºC)
Figura.A.I.4- vt = f(T) para dp=107,5 µm
211
Apêndice I - Caracterização da areia
3.0E-02
vmf (m/s)
2.5E-02
2.0E-02
1.5E-02
1.0E-02
y = -2.18E-11x3 + 5.55E-08x2 - 5.60E-05x + 3.71E-02
R2 = 1.00E+00
5.0E-03
0.0E+00
0
200
400
600
800
1000
T(ºC)
Figura A.I.5- vmf = f(T) para dp=142,5 µm
1.00
vt (m/s)
0.80
0.60
0.40
y = 2.68E-07x2 - 6.64E-04x + 9.29E-01
R2 = 9.99E-01
0.20
0.00
0
200
400
T(ºC)
600
800
1000
FiguraA.I.6- vt= f(T) para dp=142,5 µm
0.10
vmf (m/s)
0.08
0.06
0.04
y = -6.31E-11x3 + 1.63E-07x2 - 1.67E-04x + 1.14E-01
R2 = 1.00E+00
0.02
0.00
0
200
400 T(ºC)
600
800
Figura A.I.7- vmf= f(T) para dp=282,5 µm
212
1000
Apêndice I - Caracterização da areia
2.50
vt (m/s)
2.00
1.50
y = 2.3417e-0.0003x
R2 = 0.9998
1.00
0.50
0.00
0
200
400
600
T(ºC)
800
1000
Figura A.I.8- vt= f(T) para dp= 282,5 µm
0.14
0.12
vmf (m/s)
0.10
0.08
0.06
0.04
y = -8.52E-11x3 + 2.22E-07x2 - 2.33E-04x + 1.64E-01
R2 = 1.00E+00
0.02
0.00
0
200
400
T(ºC)
600
800
1000
Figura A.I.9- vmf= f(T) para dp= 357,5 µm
3.50
3.00
vt (m/s)
2.50
2.00
1.50
y = 4.27E-10x3 - 9.16E-07x2 + 1.36E-04x + 2.95E+00
R2 = 1.00E+00
1.00
0.50
0.00
0
200
400
600
800
1000
T(ºC)
Figura A.I.10- vt= f(T) para dp= 357,5 µm
213
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Apêndice II. Calibração dos aparelhos de medida e respectivas
incertezas
Neste apêndice apresentam-se todas as calibrações feitas aos vários aparelhos de
medida, bem como o procedimento experimental inerente às respectivas calibrações e ainda.as
incertezas das calibrações efectuadas.
AII.1 Calibração dos transdutores usados na determinação da queda de pressão no leito
fluidizado e ao longo da zona de transporte.
Todos os transdutores de pressão usados, quer no leito fluidizado, quer na calibração das
placas de orifício são da marca Omega. Uns são transdutores diferenciais cujo modelo é
PX143-05BD5V, que cobrem uma gama de pressões diferenciais entre 5 e –5 psi, (3,45x104 a
-3,45x104 Pa) outros PX142-005D5V, cuja gama de pressões diferenciais varia entre 0 e 5 psi
(0 a 3,45x104 Pa) e ainda se usaram outros transdutores com o modelo PX142-002D5V que
permitem leituras entre 0 e 2 psi (0 a 1,38x104 Pa).
As calibrações do modelo PX143 foram feitas com um manómetro de água, tendo sido
montado um sistema de acordo com o esquema da Figura A.II.1. Inicialmente a toma do
transdutor correspondente à posição de alta pressão (P2) foi ligada a um dos braços do
manómetro de água, e a outra, correspondente à posição de baixa pressão (P1) ficou aberta
para a atmosfera, assim como o outro braço do manómetro de água.
Para cada desnível imposto no manómetro de água é determinado o valor médio da
tensão correspondente, valor este adquirido pelo sistema de aquisição de dados instalado.
Este procedimento repete-se fazendo a troca das tomas do transdutor para se conseguir
assim, obter o ramo descendente da função de calibração.
215
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Legenda:
A – Reservatório de água;
B – Válvula de regulação fina;
C – Manómetro de água em U;
D – Transdutor de pressão;
E – Válvula de by-pass;
F – Fonte de alimentação;
G – Placa de aquisição de dados;
H – Computador
Figura A.II.1 - Esquema de instalação para calibração dos transdutores de pressão diferencial
Em todas as rectas de ajuste obtidas, a diferença de pressão foi lida em mmH2O e a
tensão em Volt.
Apresentam-se em seguida os gráficos e as curvas de calibração obtidas
experimentalmente para um dos três transdutores de pressão correspondentes ao modelo
PX143-05BD5V.
diferença de pressão (mmH2O)
3600
2400
y = 1419.6x - 4947.4
R2 = 0.9998
1200
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
-1200
Fabricante
y = 1388x - 4858
R2 = 1
-2400
ensaio
fabricante
-3600
Tensão(V)
Figura A.II.2 Transdutor 1-Curva de calibração do PX143-05BD5V
216
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Na zona de transporte bem como no leito foram usados transdutores da marca PX142.
As respectivas curvas de calibração foram as fornecidas pelo fabricante, dada a grande
concordância verificada entre as curvas experimentais e as fornecidas.
Para o transdutor PX142-005D5V, que cobre a gama de pressões entre 0 e 5 psi (0 a
3,45x104 Pa) a curva de calibração fornecida é a seguinte:
diferença de pressão (mm H2O)
4000
3500
y = 703.40x - 703.40
R2 = 1.00
3000
2500
2000
1500
1000
500
0
0
1
2
3
4
5
6
7
Tensão(V)
Figura AII.3- Transdutor 2- Curva de calibração do transdutor PX142-005D5V
Para o transdutor PX142-002D5V, que cobre a gama de pressões entre 0 e 2 psi (0 a
1,38x104 Pa) a curva de calibração fornecida é a seguinte:
diferença de pressão(mm H2O)
1600
1400
1200
1000
y = 281.36x - 281.36
R2 = 1
800
600
400
200
0
0
1
2
3
4
Tensão(V)
5
6
7
Figura A.II.4 - Transdutor 3- Curva de calibração do transdutor PX142-002D5V
O transdutor 1 referido na Figura A.II.2. foi o que se usou para a calibração das três
placas de orifício usadas para medição dos caudais de gases. Também se usou durante algum
217
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
tempo na secção 1, correspondente ao topo da zona de transporte. O transdutor 2, cuja curva
de calibração se apresenta na Figura A.II.3 foi usado na secção 2 da zona de transporte acima
da flange aí instalada. Mais tarde também se usou outro transdutor igual a este que se ligou à
secção 1. Para a secção 3 da zona de transporte e para a determinação da pressão do leito
usaram-se dois transdutores do tipo 3, correspondentes ao modelo apresentado na Figura
A.II.4.
Como as curvas de calibração usadas foram as fornecidas pelo fabricante a incerteza
associada a cada uma delas é também a fornecida pelo fabricante e é mostrada na tabela
seguinte:
Tabela A.II.1 Incertezas associadas às curvas de calibração dos transdutores
Incerteza
(Pp)
Gama de
Pressão
(psi)
mmH2O
Pa
PX142- 002D5V
0-2
4.08
40,0
PX142- 005D5V
0-5
8,50
83,3
PX143- 05BD5V
±5
10,20
101,86
Modelo e número
Na figura abaixo mostra-se o esquema da instalação correspondente à colocação dos
transdutores mencionados nas respectivas secções da zona de transporte.
Transdutor 1
Transdutor 2
Transdutor 3
Figura A.II.5 – Esquema de instalação da posição dos transdutores na coluna
A.II.2 Calibração dos medidores de caudal de gás
Os medidores de caudal usados para determinação do caudal de ar e de propano a
circular na câmara de combustão são placas de orifício previamente calibradas. Tendo em
218
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
atenção a gama de caudais a usar, a calibração da placa orifício para o propano será feita pelo
método do deslocamento positivo que se descreve à frente. Para o ar os caudais são
demasiado elevados para recorrer ao método anterior, e calibraram-se duas placas de orifício
recorrendo a um analisador de CO2. Neste caso foi necessário calibrar inicialmente um
rotâmetro 2D-150S para medição do caudal de CO2 e para esse efeito recorreu-se novamente
ao método do deslocamento positivo.
Enquanto que para um rotâmetro, a calibração relaciona a posição do flutuador com o
caudal que o atravessa, a calibração de um medidor de orifício relaciona o caudal de gás que o
atravessa com a queda de pressão que o fluido sofre ao atravessar o orifício. Neste trabalho
ligaram-se as tomas de pressão de cada uma das placas de orifício ao respectivo transdutor de
pressão diferencial que por sua vez se ligou ao sistema de aquisição de dados. Como já se
referiu cada uma das placas de orifício foi ligada a um transdutor da marca PX143-05BD5V.
Assim, a curva que se obteve foi uma curva de caudal em função da tensão correspondente à
queda de pressão no orifício. Por outro lado, com este procedimento calibra-se de uma só vez
toda a cadeia de medida composta por placa de orifício, transdutor de pressão e sistema de
aquisição de dados.
A.II.2.1 Calibração da placa orifício para o propano e do rotâmetro para o CO2
A placa orifício para o propano está apertada entre duas flanges soldadas a dois tubos de
aço galvanizado com ¼ de polegada (diâmetro interior 9,62 mm e diâmetro exterior
13,8 mm). Duas placas orifício, feitas em chapa de latão com furos chanfrados a jusante
foram calibradas. Uma delas com furo de 2,95 mm foi calibrada para a pressão relativa de 1
bar e outra com furo de 1mm, foi calibrada para a pressão relativa de 400 mbar. As tomas de
pressão do respectivo transdutor foram posicionadas nos dois tubos a 25 mm quer a montante
quer a jusante da placa orifício. Os comprimentos dos tubos antes e depois da placa orifício
são respectivamente 270 mm e 170 mm.
A técnica empregue nas duas calibrações foi, como já se referiu, o Método do
Deslocamento Positivo. A aplicação deste método requer uma instalação como a representada
na Figura A.II.6.
A curva de calibração do rotâmetro do tipo 2D 150S para calibração do caudal de CO2
foi feita à pressão relativa de 1 bar e obteve-se uma relação entre a posição do flutuador e o
219
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
caudal mássico de gás que o atravessa. A curva resultante encontra-se apresentada na Figura
A.II.7. As curvas de calibração para as duas placas orifício referidas que relacionam a tensão
lida pelo transdutor com o caudal mássico de propano, encontram-se representadas nas
Figuras A.II.8.e A.II.9 respectivamente.
No método do deslocamento positivo o gás cujo caudal se pretende conhecer é
introduzido num recipiente inicialmente cheio de água. Por força da introdução do gás, a água
é empurrada para fora do recipiente sendo medida a massa que sai num dado intervalo de
tempo. Quantificando-se a massa de água que saiu do depósito no intervalo de tempo
determinado, conhece-se de imediato o caudal de gás que foi introduzido no depósito. Se
assim é, então analise-se o que se passa num intervalo de tempo elementar dt, no recipiente
onde é introduzido o gás durante o processo de calibração para se poder avaliar a precisão do
método.
O balanço mássico ao depósito no intervalo de tempo dt, admitindo que o propano é
insolúvel no líquido e considerando que o escoamento se desenvolve em regime uniforme,
mostra que a variação de massa de ar contida no volume de controlo está relacionada com o
caudal de ar que entra
•
dmgvc = m ent × dt
(A.II.1)
•
d (vg × ρ g ) = m g × dt
(A.II.2)
e que a variação da massa de líquido contida no volume de controlo está relacionada o caudal
de água que sai
•
dmlvc = m sai × dt
(A.II.3)
d (vL × ρ L ) = − ρ L × Q L ×dt
(A.II.4)
Considerando o líquido um fluido incompressível (ρ ≈ const),
dvL = −Q L ×dt
(A.II.5)
Por outro lado, se o recipiente tiver paredes rígidas
vL + vg = v = cons ⇒ dvL + dvg = 0 ⇒ dvL = − dvg
substituindo (A.II.6) em (A.II.5) obtém-se
220
(A.II.6)
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
dt =
dvg
(A.II.7)
QL
Derivando a expressão (A.II.2) e conjugando com (A.II.7) chega-se a
ρ g × dvg + vg × d ρ g = ρ g × Q g ×
dvg
(A.II.8)
QL
rearranjando a expressão e integrando, entre um instante inicial em que o reservatório possui
um volume de gás vg1 e o instante final em que o volume ocupado pelo gás é vg2, obtém-se:
vg 2
ρg 2
 Qg 
 − 1 × ln vg  vg 1 = ln ρ g  ρ g 1
 QL 
(A.II.9)
sendo a evolução do gás isotérmica pg2/pg1 = ρg2/ρg1. Substituindo temos que,
 ln( pg 2 / pg1 ) 
Qg = QL × 1 +

ln(vg 2 / vg1 ) 

(A.II.10)
se se fizer vg1→0 então Qg = QL . Portanto, para se medir com precisão o caudal volúmico de
gás que entra no recipiente D, ou se fazem ensaios com o volume inicial de gás no depósito
nulo, ou é necessário conhecer o seu valor inicial de forma a corrigir Qg de acordo com a
expressão (A.II.10)
Rede de
água
Exterior
V3
V4
R
M
MU
MC
V2
V1
Saídas de pressão
se necessário
T
V5
D
G
B
G -Gás cujo o caudal se pretende medir
R - Redutor de pressão variável
M - Manómetro
MC - Medidor de caudal a calibrar
V1 - Válvula de regulação de caudal
MU - Manómetro de água em U
P
b
D - Depósito de 220 kg de capacidade
B - Balança
b - Balde
P - Purga
V2, V3, V4, V5 - Válvulas de corte
Figura A.II.6 Esquema da instalação usada na calibração das placas orifício para o propano e para um
rotâmetro 2D-150S para medição do caudal de CO2 – Método do deslocamento positivo.
221
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Passa-se de seguida a descrever o procedimento experimental necessário à calibração da
placa de orifício para o propano e do rotâmetro de CO2:
- Fechar a válvula V2 que introduz o gás no depósito e abrir a válvula V5 que dá acesso
ao exterior;
- Com a válvula V5 aberta, abrir a válvula V3 de entrada de água e encher o depósito D
até que comece a sair água pela purga P. Nesta altura fechar a válvula de entrada de
água V3;
- Esperar que a pressão estabilize dentro do depósito e fechar a válvula V5;
- Abrir o circuito do gás por abertura de um passador de uma garrafa de propano ou de
Dióxido de Carbono consoante a calibração a efectuar;
- Escolher e fixar a pressão de calibração accionando o redutor de pressão R. Na
calibração do circuito correspondente quer ao CO2 quer ao propano fixou-se a pressão
relativa no valor 1 bar. A verificação da pressão pode ser feita por leitura do manómetro
que está acoplado ao redutor de pressão;
- Regular e fixar o caudal accionando a válvula V1. No caso do propano a leitura da
tensão permite escolher o caudal, no caso do CO2 é a posição do flutuador que permite
fazer essa escolha;
- Colocar à saída do tubo de pesca um recipiente para recolha da água a rejeitar;
- Abrir a válvula V2 e fechar a válvula V4, introduzindo assim o gás no depósito;
- Estar atento ao manómetro em U (MU), pois a pressão começará a subir, até que comece
a sair água do depósito pelo tubo de pesca altura em que a pressão estabiliza dentro
deste;
- Introduzir o balde b previamente tarado debaixo do tubo de pesca accionando em
simultâneo o cronómetro;
- Ler e registar o desnível no manómetro em U, e se verificar variação deste durante o
ensaio, efectuar a leitura no início e fim do ensaio (∆P);
- Accionar o dispositivo que permite a leitura da tensão que sai do transdutor de pressão
correspondente ao caudal que circula. Tomar nota dos valores;
- Esperar o tempo necessário para que o balde fique praticamente cheio, altura em que se
volta a introduzir o recipiente de recolha debaixo do tubo de pesca, parando em
simultâneo a contagem do tempo e tomando nota do seu valor (∆t);
- Fechar a válvula V2 e abrir a válvula V4 que envia o gás para o exterior (no caso do
propano é conveniente que o gás seja enviado para atmosfera exterior) ;
- Pesar o balde cheio de água e anotar o seu valor (mh);
222
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
- Ler e registar a temperatura e pressão ambiente;
- Voltar a encher o depósito, seleccionar um novo caudal de água e repetir o procedimento
anterior tantas vezes quantas as necessárias para obter a curva de calibração que
pretende.
O caudal mássico de gás pode ser determinado pela seguinte expressão:
•
mg =
mh
PM × (∆P + Pa )
×
∆t × ρ h
R × Ta
(A.II.11)
Apresenta-se de seguida a curva de calibração obtida para o rotâmetro 2D-150S para o
CO2 à pressão relativa de 1 bar e as duas curvas de calibração para as placas de orifício para o
propano.
Caudal mássico de CO2 (kg/h)
0.60
0.50
y = 5.49E-02x - 7.92E-03
R2 = 9.99E-01
0.40
0.30
0.20
pontos experimentais
0.10
0.00
0
1
2
3
4
5
6
7
8
9
10
11
Posição do flutuador
Figura A.II.7 Curva de calibração do rotâmetro 2D 150S, com CO2 à pressão relativa de 1 bar,
utilizando o método do deslocamento positivo
Como já foi referido, pelo mesmo método do deslocamento positivo calibraram-se as
placas orifício correspondente ao propano. Foram feitas calibrações a duas placas de
dimensões diferentes para se poder ter uma maior gama de caudais de trabalho caso venha a
ser necessário. Os resultados dessas calibrações vêm apresentados nas figuras seguintes:
223
Caudal mássico de propano(kg/h)
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
4.0
3.5
3.0
2.5
2.0
y = 42.504x3 - 489.75x2 + 1885.5x - 2421.8
R2 = 0.9952
1.5
1.0
Pontos experimentais
0.5
0.0
3.50
3.55
3.60
3.65
3.70
3.75
3.80
3.85
3.90
3.95
4.00
Tensão(V)
Figura A.II.8- Curva de calibração do medidor de orifício para propano, dor= 2,95 mm à pressão
relativa de 1 bar , utilizando o método do deslocamento positivo
caudal de propano (kg/h)
1.80
1.60
1.40
1.20
1.00
0.80
y = 0.778x3 - 10.409x2 + 46.976x - 70.151
R2 = 0.9977
0.60
0.40
pontos experimentais
0.20
0.00
3.4
3.6
3.8
4
4.2
4.4
4.6
4.8
5
Tensão(V)
Figura A.II.9- Curva de calibração do medidor de orifício para propano, dor= 1 mm à pressão relativa
de 400 mbar, utilizando o método do deslocamento positivo
Depois de obtidas as curvas de calibração passou-se então a fazer a análise de incertezas
das respectivas calibrações. Uma vez que no caso deste trabalho foi apenas usada a curva de
calibração do propano correspondente à Figura A.II.9, foi só para essa que se fez a respectiva
análise de incertezas.
224
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Para a análise das incertezas das várias variáveis medidas, foi necessário considerar os
erros sistemáticos e aleatórios, deste modo a incerteza total é dada por
U x = Bx 2 + Px 2
(A.II.12)
em que:
Ux – incerteza total associada à medição da grandeza x;
Px – incerteza aleatória associada à medição da grandeza x;
Bx – incerteza sistemática associada à medição da grandeza x;
Assumindo que não existem incertezas sistemáticas e aleatórias correlacionadas
j −1
j
Bx2 = ∑ θi2 ⋅ Bi2 + 2 ⋅ ∑
i =1
j
∑ θ ⋅θ
i =1 k =i +1
i
k
⋅ Bik
(A.II.13)
j
Px2 = ∑ θi2 ⋅ Pi 2
(A.II.14)
i =1
onde Bi e Pi são as incertezas sistemáticas e aleatórios da variável Xi, Bik é uma estimativa
para o erro sistemático em Xi e Xk e θi =
∂x
.
∂X i
Rotâmetro de CO2
Tendo em consideração a equação A.II.11, através da qual se obtiveram os caudais
mássicos de CO2, o cálculo da incerteza sistemática associada a esses caudais é dada por:
2
B
2
.
mg
2
2
2
2
 .
  .
  .
  .
  .
  .
∂
m
∂
m
∂
m
∂
m
∂
m
∂mg
g
g
g
g
g
=
⋅ Bmh  + 
⋅ B ∆t  + 
⋅ B∆P  + 
⋅ BPa  + 
⋅ BTa  + 
⋅ Bρ
h
 ∂mh
  ∂∆t
  ∂∆P
  ∂Pa
  ∂Ta
  ∂ρ

 
 
 
 
  h




2
(A.II.15)
considerando B( ∆P + Pa ) como um só termo, obtém-se através da equação anterior
B .
 mg
 .
 mg
2
2

B
 =  Bmh  +  B ∆t  +  ( ∆P + Pa )
  mh   ∆t   ∆P + Pa


2
2
  BTa   Bρ h
 + 
 + 
  Ta   ρ h



2
(A.II.16)
em que
225
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
B∆P + Pa =
( B∆P ) + ( BPa )
2
2
(A.II.17)
Os erros sistemáticos que foram identificados são
erro da medição da massa de água, sendo está igual a metade da menor divisão da
escala utilizada (balança Sartorius)
Bmh =
0, 01
= 0, 005 kg
2
erro da leitura do tempo, e é igual a metade da menor divisão da escala utilizada
(cronómetro Rucanor)
B∆t =
0, 01
= 0, 005 s
2
erro na leitura da diferença de pressão, associado à leitura do manómetro de água, e é
igual a metade da menor divisão da escala utilizada (papel milimétrico)
B∆P =
1
= 0,5 mmH 2O
2
Desprezando a incerteza de ρh tem-se
B∆P = 4,89 Pa
erro na leitura da pressão atmosférica, associado à leitura do barómetro, e é igual
metade da menor divisão da escala utilizada
BPa =
1
= 0,5 mmHg = 66, 67 Pa
2
erro na leitura da temperatura, associado à leitura da medidor de temperatura, e é igual
metade da menor divisão da escala utilizada
BTa =
1
= 0,5 º C
2
O erro aleatório considerado foi o associado à regressão linear, utilizada para obter a
curva de calibração do rotâmetro, que é dado por
 N
2 
 ∑ (Yi − m ⋅ X i − b ) 

P. = 2 ⋅  i =1
mg
Np − 2




226
0,5
(A.II.18)
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
em que Np é o número de pontos utilizado na regressão, m e b são os coeficientes da recta de
ajuste, Yi é o valor do caudal mássico experimental de CO2 obtido através do método do
deslocamento positivo e Xi o valor da posição do flutuador no rotâmetro.
Assim as incertezas dos caudais mássicos de CO2 obtidos através do rotâmetro, estão
representadas na figura seguinte.
30%
UmCO2/mCO2 (%)
25%
20%
15%
10%
5%
0%
0
1
2
3
4
5
6
7
8
9
10
Posição do flutuador
Figura A.II.10 Incerteza do caudal mássico de CO2 para cada posição do rotâmetro
Placa orifício – Propano
Tendo sido o mesmo método do deslocamento positivo usado na calibração desta placa
orifício, os valores experimentais dos caudais de propano foram também obtidos pela equação
A.II.11. Então o cálculo da incerteza relativa à medida do caudal de propano considerou-se o
erro relativo à calibração da placa orifício, dado pela equação (A.II.15) e foi também
contabilizada a incerteza associada à leitura da tensão, obtida através do sistema de aquisição
de dados, que utiliza uma placa analógica/digital (A/D) de 16 bits de resolução, para um sinal
de ±15 V . A incerteza que resulta da digitalização do sinal é igual a metade do menor bit
significativo (LSB). Para uma placa de 16 bits, 1 LSB é igual a:
10 10
= 16 = 1,53 × 10−4 V
n
2
2
(A.II.19)
1
⋅1.53 × 10−4 = 7, 63 ×10 −5 V
2
(A.II.20)
1 LSB =
BA / D =
227
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
O erro aleatório considerado foi o associado à linha de tendência, utilizada para obter a
curva de calibração da placa orifício do propano, que é dado pela seguinte expressão
1/ 2
P.
m Propano
2
 N
3
2
 ∑ ( yi − a ⋅ X i − b ⋅ X i − c ⋅ X i − d ) 

= 2 ⋅  i =1
Np − 2




(A.II.21)
Assim as incertezas dos caudais mássicos de propano estão representadas na figura seguinte:
60%
Umpro/mpro [%]
50%
40%
30%
20%
10%
0%
3.5
3.7
3.9
4.1
4.3
4.5
4.7
4.9
Tensão (V)
Figura A.II.11 Incerteza do caudal mássico de propano
A.II.2.2 Calibração da placa orifício para o ar
Esta placa está apertada entre duas flanges soldadas a dois tubos de aço galvanizado
com de 3/8 polegada (diâmetro interior 17,2 mm e diâmetro exterior 21,4 mm). A placa
orifício é feita em chapa de latão com um furo de 5 mm, chanfrado a jusante. As tomas de
pressão para o transdutor foram posicionadas nos dois tubos a 35 mm quer a montante quer a
jusante da placa orifício. Os comprimentos dos tubos antes e depois da placa orifício são
respectivamente 965 mm e 465 mm.
Esta placa orifício foi calibrada para 1 bar relativo e também para 200 mbar e 400 mbar,
com um analisador de CO2, que por já se encontrar calibrado não foi necessário proceder a
uma calibração prévia.
Para isso recorreu-se à seguinte instalação experimental:
228
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
TP
PO
+
V4
R2
M2
Ar Comprimido
PA
Analisador
CO2
C
V3
Atmosfera
RO
R1
M1
V1
R1/R2 - Redutor de pressão variável
M 1/M2 - Manómetro
V1, V4 - Válvulas de corte
V2/V3 - Válvula de regulação de caudal
RO - Rotâmetro
PO - Placa orifício
TP - Transdutor de pressão
PA - Placa de aquisição
C - Computador
CO2
Figura A.II.12- Esquema da instalação usada para calibrar as placas orifício correspondente ao ar
usando um analisador de CO2
Procedimento experimental:
- Anotar a temperatura e pressão ambiente;
- O regulador de pressão R2 foi regulado de modo que a pressão relativa do ar no
manómetro M2 fosse igual a 1 bar;
- O caudal de ar foi regulado através da abertura e fecho da válvula de agulha V3;
- A pressão efectiva do dióxido de carbono foi fixada com ajuda do regulador R1 no valor
de 1 bar (condição de calibração do rotâmetro);
- O caudal de CO2 foi regulado à custa da válvula V2. Tendo em atenção a posição do
flutuador no rotâmetro RO, o caudal é já conhecido uma vez que a calibração deste
rotâmetro foi previamente feita e está apresentada na Figura A.II.7;
- Para uma posição definida da válvula V3 e para uma posição do flutuador do rotâmetro
de CO2 também fixa, anota-se a leitura do analisador de CO2 que se refere à fracção
volúmica seca de dióxido de carbono, na mistura de ar mais dióxido de carbono que aí
chega.
229
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
- Para cada ensaio feito activa-se o sistema de aquisição de dados e a tensão média lida
pelo transdutor de pressão que está ligado à placa de orifício, fica registada;
- Este procedimento é repetido para várias posições da válvula V3, mantendo o flutuador
do rotâmetro RO numa mesma posição.
Repetiu-se todo este procedimento tendo o cuidado de abrir o regulador de pressão R2
para que a pressão relativa do ar no manómetro M2 fosse agora de 400 mbar.
Um balanço de massa feito ao ponto de mistura das duas correntes permite então,
determinar o caudal volúmico de ar nas condições de calibração da referida placa. A equação
de balanço é:
Qar + QCO2 = %CO2 × Qt
(A.II.22)
Qt = Qar + QCO2
(A.II.23)
e
Combinando as equações A.II.22 e A.II.23 obtém-se:
Qar =
1 − %CO2
QCO2
%CO2
(A.II.24)
O valor de QCO2 è determinado recorrendo à respectiva curva de calibração, Figura
A.II.7, tendo o cuidado de converter o valor do caudal mássico daí retirado em caudal
volúmico, pelas condições de pressão e temperatura ambiental. Só então é introduzido na
equação A.II.24, determinando assim o caudal volúmico de ar nas mesmas condições de
pressão e temperatura. A conversão para caudal mássico de ar é feita também recorrendo às
condições de pressão e temperatura ambiente que são as do ponto de mistura das duas
correntes. A este caudal mássico corresponde uma tensão média do transdutor de pressão
diferencial que se encontra ligado à referida placa de orifício.
Apresentam-se de seguida as duas curvas de calibração obtidas para a placa orifício
correspondente ao ar às diferentes pressões.
230
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
16.0
caudal de ar (kg/h)
14.0
12.0
10.0
8.0
y = -0.42x4 + 8.78x3 - 69.78x2 + 250.19x - 333.15
R2 = 1.00
6.0
4.0
2.0
1ºensaio
2ºensaio
5
5.5
3ºensaio
4º ensaio
0.0
3.5
4
4.5
6
6.5
7
Tensão(V)
Figura A.II.13.- Curva de calibração da placa orifício com dor=5 mm para ar à pressão relativa de 1 bar
recorrendo ao analisador de CO2
10.0
9.0
caudal de ar (kg/h)
8.0
7.0
6.0
5.0
4.0
y = -4.14x4 + 72.71x3 - 479.09x2 + 1407.79x - 1553.47
R2 = 1.00
3.0
2.0
1ºensaio
1.0
2ºensaio
3ºensaio
0.0
3.4
3.6
3.8
4
4.2
4.4
4.6
4.8
5
5.2
Tensão(V)
Figura A.II.14.- Curva de calibração da placa orifício com dor=5 mm para ar à pressão relativa de
400 mbar recorrendo ao analisador de CO2
Todas as figuras apresentadas correspondem a calibrações feitas antes do arranque da
instalação e de acordo com estimativas previstas para caudais de ar a serem usados no
decorrer dos ensaios experimentais.
Como se pode verificar pelas Figuras A.II.13 e A.II.14, quanto mais alta for a pressão de
calibração maior é a gama de caudais com que se pode trabalhar aumentando sobretudo o
limite máximo do caudal.
Quando a instalação ficou pronta, e se começaram a fazer os primeiros ensaios de
arranque, rapidamente se verificou que a potência de aquecimento era muito baixa para
231
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
conseguir aquecer os caudais de ar necessários à auto-ignição do propano. Deste modo optouse por se usar a curva correspondente à Figura A.II.14 que permite obter caudais de ar mais
baixos. A curva de calibração apresentada na Figura A.II.13 poderá vir a ser útil em trabalhos
futuros se o objectivo for a circulação efectiva de sólidos, desde que seja possível aumentar a
potência térmica do reactor.
Passou-se em seguida a fazer a análise de incertezas correspondente à calibração da
placa orifício para o ar, representada na Figura A.II.14.
Tendo em consideração a equação A.II.24 através da qual se obteve o caudal
volumétrico de ar, o cálculo da incerteza sistemática é dado pela seguinte expressão:
2
BQar
2
 ∂ Qar
  ∂ Qar
B% CO2  + 
B
=
 ∂ % CO
  ∂QCO QCO2

 
2
2



2
(A.II.25)
Os erros sistemáticos que foram identificados são:
•
erro relativo à leitura da percentagem de CO2 pelo o analisador, correspondente a 5%
do máximo da escala do analisador que é 25%.
(B
% CO2
•
)
2
 0, 005 × 25 
−6
=
 = 1,56 × 10
 100

2
erro relativo ao caudal volúmico de CO2 é obtido através das Figura A.II.10 para a
posição 5 do flutuador
BQCO = 2,50 × 10 −6 m3 s
2
O erro aleatório considerado, foi o associado a linha de tendência utilizada para obter a
curva de calibração da placa orifício do ar que é dado pela seguinte expressão
232
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
1/ 2
PQAr
2 
 N
4
3
2
 ∑ ( yi − a ⋅ X i − b ⋅ X i − c ⋅ X i − d . X i − e ) 

= 2 ⋅  i =1
Np − 2




(A.II.26)
Assim as incertezas dos caudais volumétricos do ar obtidos através da placa orifício
correspondente a Figura A.II.14 estão representadas na figura seguinte.
10%
UQar/Qar (%)
9%
8%
7%
6%
3
3.5
4
4.5
5
5.5
Tensão (V)
Figura A.II.15.- Incerteza do caudal volumétrico do ar
Esta curva apresenta o mesmo comportamento para o caso dos caudais mássicos de ar
devido ao facto de não se ter considerado nenhuma incerteza na massa volúmica do ar à
temperatura ambiente.
A.II.3 Calibração dos aparelhos de medida para o caudal de água
A.II.3.1 Debitómetro de turbina
O processo de calibração deste aparelho é feito ligando o debitómetro directamente à
rede de água e ligando-o também ao sistema de aquisição de dados. A fonte de alimentação
usada é de 24 Volt.
O caudal de água que circula na parede de membrana do permutador, é controlado
através de uma válvula de agulha instalada no final da instalação.
233
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
O processo de calibração é o seguinte:
- Ligar a água da rede;
- Abrir a válvula de regulação para selec\cionar o caudal pretendido;
- Colocar um balde previamente tarado à saída do tubo e fazer a recolha da água com a
contagem simultânea do tempo;
- Durante o processo anterior accionar o dispositivo que permite a leitura e
armazenamento da tensão que sai do debitómetro de turbina correspondente ao caudal
de água que circula;
- Pesar o balde e anotar o seu valor (magua);
- Anotar o tempo de recolha da água (∆t);
- Seleccionar um novo caudal de água e repetir o procedimento anterior tantas vezes
quantas as necessárias para obter a curva de calibração.
O caudal de água é determinado pela expressão:
•
m ag =
M ag
(A.II.25)
∆t
A figura seguinte representa o resultado da calibração efectuada
caudal de água (kg/min)
16.0
14.0
12.0
y = 11.03x - 18.00
R2 = 1.00
10.0
8.0
6.0
4.0
Pontos experimentais
2.0
0.0
1.50
1.80
2.10
2.40
2.70
3.00
Tensão (V)
Figura A.II.16- Curva de calibração do debitómetro de turbina para medição do caudal de água
234
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Este aparelho usado para medição do caudal de água tinha como principal vantagem o
facto de se poder ligar ao sistema de aquisição de dados. Contudo, além de se obter sempre
muito ruído na aquisição do sinal a gama de trabalho era demasiado alta. Como se pode ver
pela figura A.II.16 o caudal mínimo de água era de 2 kg/min que corresponde a 120 kg/h .
A.II.3.2 Rotâmetro
Durante os primeiros ensaios verificou-se que os caudais de água medidos com o
equipamento anterior eram sujeitos a grandes flutuações e além disso a gama de caudais com
que permitia trabalhar era demasiado elevada. Por estes motivos optou-se por instalar um
rotâmetro cuja curva de calibração se apresenta de seguida. Para que não se estivesse sujeito
às flutuações da água da rede, foi colocado um redutor de pressão no ponto da abastecimento
da água ao sistema que por sua vez foi regulado para a pressão de 1,5 bar relativos.
O processo de calibração de um rotâmetro para líquidos consiste apenas no seguinte:
1.
Abrir totalmente a torneira da água da rede;
2.
Com a ajuda da válvula agulha, colocada depois do rotâmetro e neste caso na saída da
água da camisa de arrefecimento, posicionar a parte mais larga da cabeça do flutuador
numa dada cota;
3.
Recolher a água para um “goblé” previamente tarado medindo simultaneamente o tempo
com ajuda de um cronómetro;
4.
Repetir este procedimento de maneira a ter valores concordantes;
5.
Passar para outra posição do flutuador, por manipulação da válvula agulha e repetir o
procedimento experimental a partir do ponto 3.
O caudal de água é calculado novamente pela expressão
•
m ag =
M ag
∆t
(A.II.25)
Apresentando-se na figura seguinte o resultado da calibração
235
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
caudal de água (kg/h)
250
200
y = 1.99x + 3.12
R2 = 1.00
150
100
pontos experimentais
50
0
0
20
40
60
80
100
120
Posição do flutuador
Figura A.II.17.-Curva de calibração do rotâmetro para a Prel =1.5 bar para medição do caudal de água.
Como foi esta a calibração usada em todos os ensaios experimentais fez-se de seguida a
análise da respectiva incerteza.
Rotâmetro de água
Para a análise da incerteza da calibração do rotâmetro de água foram consideradas
também as incertezas sistemáticas e aleatórias.
Tendo como referência a equação A.II.25, as incertezas sistemáticas são dadas por
 B.
 mag
 m.
 ag
2
 B
 =  M ag
 M
  ag
2
  B ∆t  2
 + 

  ∆t 
(A.II.26)
As incertezas dadas pelo tempo e pela massa da água são as mesmas que foram
consideradas para o cálculo da incerteza do rotâmetro e placa orifício para o propano.
A incerteza aleatória considerada, foi a associada à linha de tendência obtida para a
curva de calibração, e vem dada por:
P.
mag
236
 N
2 
 ∑ (Yi − m ⋅ X i − b ) 

= 2 ⋅  i =1
Np − 2




0,5
(A.II.27)
Apêndice II – calibração dos aparelhos de medida e respectivas incertezas
Contabilizando então as duas componentes das incertezas (sistemática e aleatória), o
valor para Umag é de 5,17 kg/h e a curva da incerteza relativa para cada posição do flutuador
está representada na figura seguinte,
25%
Umag/mag (%)
20%
15%
10%
5%
0%
0
20
40
60
80
100
120
Posição do flutuador
Figura A.II.18- Incerteza do caudal mássico de água
237
Apêndice III – Análise de incertezas dos parâmetros experimentais calculados
Apêndice III. Análise de incertezas dos parâmetros experimentais
calculados
A equação que permitiu determinar o coeficiente global de transferência de calor
experimental baseou-se na variação da entalpia da água e é a seguinte,
exp
hglo
=
mag c p (Tags − Tage )
Ap (TL − Tgscorr )
 TL − Tw 
ln  corr
 Tgs − Tw 


(A.III.1)
A incerteza total associada a esta expressão é dada pela seguinte equação
U
2
hglo
 ∂m
=  ag U mag
 ∂h
 glo
2
2
2
  ∂Tags
  ∂T
  ∂A
U Tags  +  age U Tage  +  p U Ap
 + 
 
 
  ∂hglo
  ∂hglo
  ∂hglo
2
2
  ∂TL
  ∂Tgscorr

U TL  + 
U Tgs 
 + 
 

  ∂hglo
  ∂hglo

(A.III.2)
e não se entra com o erro associado à temperatura da parede que aparece na equação A.III.1
porque esta foi uma temperatura estimada.
É então preciso analisar os erros associados às seguintes variáveis:
- Caudal de água;
- Temperatura;
- Área.
Os erros associados ao caudal de água são apenas as incertezas da calibração
apresentadas na Figura A.II.18, e como já aí foi referido o valor é, Umag = 5,17 kg/h.
239
2
Apêndice III – Análise de incertezas dos parâmetros experimentais calculados
Os erros associados à temperatura são,
- erros sistemáticos identificados como:
erros associados aos termopares usados na leitura de todas as temperaturas, termopares
tipo K, sendo o erro fornecido pelo fabricante o seguinte,
BT = 0,4% Tlida
erro de conversão analógico/digital da placa de aquisição UPC601-T
1LSB =
10 10
= 14 = 6,10 × 10−4
n
2
2
BA / D =
1
⋅ 6,10 × 10−4 = 3, 05 × 10 −4
2
- erros aleatórios
Estes erros são associados ao número de leituras feitas em cada ensaio e são calculados
recorrendo às Tabelas t de Student, considerando um limite de confiança de 95% e n-2 graus
de liberdade, sendo n o número de leituras efectuadas, σ o desvio padrão e t o parâmetro de
Student que neste caso é igual a 1,96.
PT =
t ⋅σ
n
Contabilizando todos estes erros o valor da incerteza total associada à temperatura vem dada
pela seguinte expressão,
2
2
2
 U T   BT   BA / D   PT 

 =   +
 + 
 T   T   tensao   T 
2
(A.III.3)
O erro associado à determinação da área é apenas um erro sistemático, referente a metade
da menor divisão do aparelho de medida, que neste caso foi uma fita métrica.
BA =
0, 001
m
2
Tendo em atenção a equação A.III.2 e os vários erros referidos, calculou-se a incerteza
total relativamente ao coeficiente global determinado experimentalmente. Esse cálculo foi
apenas feito para dois dos ensaios correspondentes a cada granulometria estudada, sendo o
240
Apêndice III – Análise de incertezas dos parâmetros experimentais calculados
critério de escolha, a temperatura máxima e mínima do leito com que se trabalhou nos ensaios
sem combustão e o caudal de ar de 1kg/h.
Apresenta-se então a tabela dos resultados obtidos,
Tabela A.III.1 Incerteza relativa nos valores de hgloexp
dp
(µm)
107,5
142,5
180
282,5
357,5
TL
hglo
2
Uhglo/hglo
(ºC)
(W/m K)
(%)
400
11,31
18,49
660
15,67
18,23
400
6,68
38,08
700
11,98
18,31
400
6,94
19,56
700
7,56
18,42
400
7,45
37,92
700
8,94
18,55
400
4,86
20,22
700
7,40
18,29
241
Apêndice IV - Propriedades da mistura gasosa
Apêndice IV. Propriedades da mistura gasosa
As propriedades da mistura gasosa podem influenciar a hidrodinâmica do escoamento,
bem como a transferência de calor do leito para a água de arrefecimento. Nos ensaios com
combustão, tem de ser feita uma análise dessas mesmas propriedades, tendo em atenção a
temperatura do leito à qual se dá a reacção e a riqueza da mistura, definida pelo parâmetro, r.
As propriedades da areia não vão ser contabilizadas para o cálculo das propriedades finais da
mistura gasosa, já que, devido às condições de borbulhamento no leito, a porosidade na zona
de transporte é muito próxima de um.
As propriedades da mistura gasosa a estimar para cada ensaio de combustão, são as
seguintes:
- massa volúmica - ρg ;
- viscosidade - µg ;
- calor específico a pressão constante - cpg ;
- condutibilidade térmica - kg
A.IV.1 Estimativa da composição da mistura gasosa
Nas condições de operação, os valores de riqueza da mistura, r com que se trabalhou
situaram-se na gama: 1,6 < r < 1,8. Estes valores de r, obtidos de acordo com a equação 4.23
apresentada no Capítulo 4, permitem classificar a reacção como uma combustão redutora, que
nas condições reais é voluntária e não se deve a uma má regulação do equipamento de queima
Nesta região borbulhante de um queimador circulante, ou mesmo de um queimador
borbulhante, o caudal de ar é frequentemente inferior ao estequiométrico, de modo que a
243
Apêndice IV - Propriedades da mistura gasosa
queima é redutora. Este tipo de combustão redutora é muitas vezes usado quando se visa a
produção de calor, que foi também o um dos objectivos deste trabalho experimental.
A reacção de combustão a considerar é a que já foi referida no Capítulo 4, e que de novo
se volta a escrever,
5
5
C3 H 8 + (O2 + 3, 76 N 2 ) → n1CO2 + n2CO + n3 H 2O + n4 H 2 + × 3, 76 N 2
r
r
(4.23)
onde:
r =1/(1-d), sendo d o defeito de ar.
Os valores de r são determinados de acordo com a equação 4.24 do Capítulo 4,
r=
( A / C )est
( A / C )real
(4.24)
sendo (A/C)est =15.64 e os valores de (A/C)real obtidos de acordo com a gama de operação para
os caudais de ar e propano usados.
O caudal de ar e de propano situaram-se na seguinte gama,
0,85 < mar(kg/h) < 1,2
então
e
0,1 < mpro (kg/h) < 0,12
8,5 < (A/C)real < 10
o que permite através da equação 4.24 calcular os valores de r acima referidos.
Para saber os valores correspondentes a n1, n2, n3, e n4, é necessário dispor de 4 equações;
ora os balanços de massa aos elementos presentes: C, O, H e N apenas conduzem a 3
equações, já que o azoto é inerte. Há pois necessidade de recorrer a uma equação de
dissociação. Como se supôs inicialmente que não existia O2 livre nos produtos, ver equação
4.23, a reacção de equilíbrio do gás de água é a mais adequada para se aplicar neste caso
CO2 ( g ) + H 2 ( g ) ↔ H 2O( g ) + CO( g )
com a constante de dissociação Kp dada por
244
(A.IV.1)
Apêndice IV - Propriedades da mistura gasosa
Kp =
pCO pH 2O
pH 2 pCO2
e definindo a pressão parcial de cada componente como:
pi =
ni
P
nt
(A.IV.2)
então a constante de dissociação, kp´, correspondente à reacção A.IV.1., em termos de moles
dos componentes, é dada pela expressão
k p′ =
n2 n3
n4 n1
(A.IV.3)
A equação de dissociação A.IV.1. é obtida a partir das reacções químicas em paralelo
que se estão a dar nos produtos e que caracterizam muitas vezes as reacções incompleta. São
elas:
com K p =
(A.IV.4)
CO( g ) + 1 2 O2 ( g ) → CO2 ( g )
(A.IV.5)
pH 2O
pO2 1 2 pH 2
e
com K p =
H 2 ( g ) + 1 2 O2 ( g ) → H 2O( g )
pCO2
pO2 1 2 pCO
O balanço de massa a cada um dos três elementos de acordo com a estequiometria da
equação 4.23, permite obter as seguintes equações algébricas:
C:
3 = n1 + n2
(A.IV.6)
H:
8 = 2n3 + 2n4
(A.IV.7)
O:
10/r = 2n1+ n2 + n3
(A.IV.8)
Estas três equações, juntamente com a equação a A.IV.3 são as que se vão utilizar para
estimar a composição da mistura gasosa e assim poder determinar as propriedades físicas da
referida mistura.
245
Apêndice IV - Propriedades da mistura gasosa
Para os ensaios feitos com as partículas de dp =107,5 µm e dp =142,5 µm, a temperatura
média do leito durante o processo de combustão foi de TL=720ºC. Para as partículas de
dp=180 µm essa temperatura média variou entre 780ºC para um caudal de ar de 1 kg/h, e,
730 ºC para uma caudal de ar de 1,2 kg/h. Para as outras duas granulometrias, dp= 282,5 µm e
dp=357,5 µm, e em condições de combustão semelhantes a todas as outras partículas, a
temperatura média do leito situou-se sempre entre 790 ºC e 800 ºC.
Para cada valor de temperatura média do leito foram determinados os valores de kp´,
recorrendo a valores fornecidos por Pinho (2005). A tabela seguinte refere os valores obtidos:
Tabela A.IV.1 Variação da constante de dissociação kp´ com a temperatura do leito
TLmédia
k p´
(ºC)
700
0,61
730
0,70
780
0,86
800
0,93
Considerando agora, as equações (A.IV.3), (A.IV.6), (A.IV.7) e (A.IV.8) , os valores de
kp´ apresentados na tabela A.IV.1 e ainda o facto de o valor da riqueza da mistura se situar
entre 1,6 < r < 1,8, referem-se nas tabelas seguintes os valores obtidos para n1, n2, n3, n4, nN2 e
nt para cada valor de r correspondente aos limites inferior e superior respectivamente .
Tabela A.IV.2 Número de moles de cada componente correspondente à reacção(4.23) para
r =1,6 e às diferentes temperaturas médias do leito
r =1,6
TLmedio(ºC)
nCO2
nCO
nH2O
nH2
nN2
nt
700
1,61
1,39
1,64
2,36
11,75
18,75
730
1,55
1,46
1,71
2,29
11,75
18,75
780
1,46
1,54
1,79
2,21
11,75
18,75
800
1,42
1,58
1,83
2,17
11,75
18,75
246
Apêndice IV - Propriedades da mistura gasosa
Tabela A.IV.3 Número de moles de cada componente correspondente à reacçaõ (4.23) para
r =1,8 e às diferentes temperaturas médias do leito
r =1,8
TLmedio (ºC)
nCO2
nCO
nH2O
nH2
nN2
nt
700
1,24
1,76
1,19
2,81
10,22
17,22
730
1,18
1,82
1,25
2,75
10,22
17,22
780
1,10
1,90
1,33
2,67
10,22
17,22
800
1,07
1,93
1,36
2,64
10,22
17,22
Os valores apresentados mostram pequenas diferenças nos vários valores de ni obtidos, já
que o número de moles que existe em maior quantidade é sempre o correspondente ao azoto.
Assim tomou-se o valor médio para cada componente tendo em conta a sua variação no caso
de r =1,6 e r =1,8, para cada temperatura média do leito. Como mais uma vez, esses cálculos
conduziram a valores muito próximos e tendo consciência que esses valores correspondem
apenas a uma estimativa relativamente às reacções previstas, então optou-se por considerar o
número de moles de cada componente constante e independente da temperatura média do leito.
Esses valores, bem como as fracções molares respectivas são apresentados na tabela que
se segue:
Tabela A.IV.4 Número de moles e fracção molar de cada componente a usar na avaliação das
propriedades da mistura gasosa
Total
Componentes
Nº de moles
ni
Fracçã molar
xi
CO2
CO
H2O
H2
N2
∑ni e ∑xi
1,4
1,6
1,4
2,6
11
18
0,08
0,09
0,08
0,14
0,61
1
247
Apêndice IV - Propriedades da mistura gasosa
A.IV.2 – Propriedades dos componentes puros
As propriedades dos componentes puros aqui apresentadas foram retiradas de várias
fontes bibliográficas conhecidas, nomeadamente:
1. Tabelas Termodinâmicas - Raznjevic (1970);
2. Incropera (1990);
3. Çengel (1998);
4. Howell (1984).
Propriedades para Dióxido de Carbono - CO2
0.1
k (W/mºC)
0.08
0.06
y = 7.58E-05x + 1.61E-02
R2 = 9.98E-01
0.04
0.02
0
0
200
400
600
800
1000
1200
T(ºC)
Figura A.IV.1.- Variação da condutibilidade térmica com a temperatura para o CO2 – Ref1
viscosidade (Pa.s)
6.00E-05
4.00E-05
2.00E-05
y = -1.10E-11x2 + 4.35E-08x + 1.45E-05
R2 = 9.97E-01
0.00E+00
0
200
400
600
800
1000
1200
T (ºC)
Figura A.IV.2.- Variação da viscosidade com a temperatura para o CO2 – Ref1
248
Apêndice IV - Propriedades da mistura gasosa
Para determinação do calor específico a pressão constante recorreu-se à equação
apresentada em Howell (1984), e é a seguinte:
cpg = 22,26 + 5,981x10-2T-3,501x10-5T 2+7,469x10-9T 3
273< T(K)< 1800
Nesta equação cpg vem em [kJ/kmol.K] e T em [K]
Propriedades para Monóxido de Carbono - CO
0.06
0.05
k (W/mK)
0.04
0.03
y = -1.43E-08x2 + 6.88E-05x + 2.32E-02
R2 = 1.00E+00
0.02
0.01
0
0
100
200
300
400
500
600
T(ºC)
Figura A.IV.3.- Variação da condutibilidade térmica com a temperatura para o CO – Ref2
4.00E-05
viscosidade(Pa.s)
3.50E-05
3.00E-05
2.50E-05
y = -1.76E-11x2 + 4.20E-08x + 1.69E-05
R2 = 1.00E+00
2.00E-05
1.50E-05
1.00E-05
0
100
200
300
400
500
600
T(ºC)
Figura A.IV.4.- Variação da viscosidade com a temperatura para o CO – Ref1
249
Apêndice IV - Propriedades da mistura gasosa
Para determinação do calor específico a pressão constante recorreu-se à equação
apresentada em Howell (1984),
cpg = 28,16 + 0,1675x10-2T+0,5372x10-5T2-2,222x10-9T3
273< T(K)< 1800
Nesta equação cpg vem em [kJ/kmol.K] e T em [K]
Propriedades para vapor de água - H2O
0.07
k (W/mK)
0.06
0.05
0.04
y = 3.22E-08x2 + 6.34E-05x + 1.69E-02
R2 = 9.99E-01
0.03
0.02
0
100
200
300
400
500
600
700
T(ºC)
Figura A.IV.5.- Variação da condutibilidade térmica com a temperatura para H2O – Ref1
3.50E-05
viscosidade(Pa.s)
3.00E-05
2.50E-05
2.00E-05
y = 3.57E-08x + 9.12E-06
R2 = 1.00E+00
1.50E-05
1.00E-05
0
100
200
300
400
500
600
700
T(ºC)
Figura A.IV.6.- Variaçaõ da viscosidade com a temperatura para o H2O – Ref1
250
Apêndice IV - Propriedades da mistura gasosa
Para determinação do calor específico a pressão constante recorreu-se à equação
apresentada em Howell (1984),
cpg = 32,24 + 0,1923x10-2T+1,055x10-5T2-3,595x10-9T3
273< T(K)< 1800
Nesta equação cpg vem em [kJ/kmol.K] e T em [K]
Propriedades para o Hidrogénio - H2
0.6
k (W/mºC)
0.5
0.4
0.3
0.2
y = 3.46E-04x + 1.77E-01
R2 = 1.00E+00
0.1
0.0
0
200
400
600
800
1000
T(ºC)
Figura A.IV.7- Variação da condutibilidade térmica com a temperatura para H2 – Ref3
2.50E-05
Viscosidade (Pa.s)
2.00E-05
1.50E-05
1.00E-05
y = -4.55E-12x2 + 1.92E-08x + 8.43E-06
R2 = 1.00E+00
5.00E-06
0.00E+00
0
100
200
300
400
500
600
700
800
900
T(ºC)
Figura AIV.8.- Variação da viscosidade com a temperatura para o H2 – Ref1
251
Apêndice IV - Propriedades da mistura gasosa
Para determinação da calor específico a pressão constante recorreu-se à equação
apresentada em Howell (1984):
cpg = 29.11 - 0,1916x10-2T+0,4003x10-5T2-0,8704x10-9T3
273< T(K)< 1800
Nesta equação cpg vem em [kJ/kmol.K] e T em [K]
Propriedades para o Azoto - N2
0.1
k(W/mºC)
0.08
0.06
0.04
y = 5.60E-05x + 2.63E-02
R2 = 9.98E-01
0.02
0
0
200
400
600
800
1000
1200
T(ºC)
Figura A.IV.9- Variação da condutibilidade térmica com a temperatura para N2 – Ref1
4.80E-05
viscosidade(Pa.s)
4.00E-05
3.20E-05
2.40E-05
y = -1.28E-11x2 + 4.07E-08x + 1.69E-05
R2 = 1.00E+00
1.60E-05
8.00E-06
0.00E+00
0
100
200
300
400
500
600
700
800
900
T(ºC)
Figura A.IV.10.- Variação da viscosidade com a temperatura para o N2 – Ref1
252
Apêndice IV - Propriedades da mistura gasosa
Para determinação da calor específico a pressão constante recorreu-se à equação
apresentada Howell (1984),
cpg = 28,90 - 0,1571x10-2 T+0,8081x10-5 T2-2,873x10-9 T3
273< T(K)< 1800
Nesta equação cpg vem em [kJ/kmol.K] e T em [K]
A.IV.3- Cálculo das propriedades da mistura gasosa
Apresentam-se agora as expressões que permitiram o cálculo das propriedades da
mistura gasosa . Todas estas propriedades à excepção da massa molecular vão ser avaliadas à
temperatura do filme Tf , tal como foi feito no caso dos ensaios sem combustão. Nessa fase de
ensaios as propriedades físicas referiram-se apenas ao ar e são apresentadas no ponto A.IV.4
deste mesmo Apêndice.
Nos ensaios com combustão e para todas as granulometrias, a temperatura do filme
variou entre os seguintes limites:
219 < Tf (ºC) < 278
• Determinação da massa molecular - Mg
5
∑M x
i i
i =1
•
= 24, 75kg / Kmol
(A.IV.9)
Determinação da massa volúmica - ρg
ρg =
PM g
RT f
(A.IV.10)
De acordo com a gama de valores para a temperatura do filme o valor de ρg variou:
0,55 < ρg (kg/m3) < 0,61
•
Determinação da calor específico a pressão constante- cpg
5
c pg = ∑ xi c pi
(A.IV.11)
i =1
253
Apêndice IV - Propriedades da mistura gasosa
De acordo com a gama de valores para a temperatura do filme o valor de cpg variou:
1262 < cpg (J/kg.K) < 1278
•
Determinação da condutibilidade térmica da suspensão - kg
De acordo com Bird et al (1960), a expressão usada para cálculo da condutibilidade
térmica da suspensão foi a seguinte:
n
k =∑
i =1
xi ki
(A.IV.12)
n
∑ xiφij
j =1
em que
M
1 
φij =
1 + i
8 Mj



−1/ 2
 k
1 +  i
  k j

1/ 2



1/ 4
Mj  

 
 M i  
2
(A.IV.13)
Para determinar o valor da condutibilidade térmica, usando estas expressões foi necessário
construir uma matriz para cada temperatura do filme dentro dos limites em que esta variou,
tendo em atenção as composições da mistura apresentadas na Tabela A.IV.4 . O resultado foi o
seguinte:
Tabela A.IV.5.- Variação da condutibilidade térmica da mistura gasosa com a temperatura do filme
•
Tf
kg
(ºC)
(W/mºC)
220
3,93x10-2
250
4,34x10-2
278
4,16x10-2
Determinação da viscosidade da suspensão - µg
De acordo com Bird et al (1960) a expressão usada para cálculo da viscosidade dinâmica
da suspensão foi a seguinte:
254
Apêndice IV - Propriedades da mistura gasosa
n
µ=∑
i =1
xi µi
(A.IV.14)
n
∑ xiφij
j =1
em que
M
1 
φij =
1 + i
8 Mj



−1/ 2
 µ
1 +  i
  µ j

1/ 2



1/ 4
Mj  

 
M
 i  
2
(AIV.15)
Também neste caso, para o cálculo do valor da viscosidade a diferentes temperaturas do
filme foi necessário construir uma matriz para cada temperatura, tendo em atenção as
composições da mistura apresentadas na Tabela AIV.4 . O resultado foi o seguinte:
Tabela AIV.6.- Variação da viscosidade da mistura gasosa com a temperatura do filme
Tf
µg
(ºC)
(Pa.s)
220
3,30x10-5
250
2,42x10-5
278
2,51x10-5
AIV.4 - Expressões usadas para cálculo das propriedades físicas do ar
Nos ensaios feitos na primeira fase deste trabalho experimental, em que se estudou a
transferência de calor na ausência de combustão apenas foi necessário saber as propriedades
do ar às diferentes temperaturas.
• Massa molecular do ar - Mar
Mar=28,74 kg/kmol
•
Massa volúmica do ar - ρar (expressão apresentada no Apêndice I)
ρ ar =
PM ar
RT f
(A.I.7)
255
Apêndice IV - Propriedades da mistura gasosa
•
Determinação da calor específico a pressão constante do ar- cpar
De acordo com a expressão apresentada em Howell (1984), o valor do calor específico a
pressão constante para o ar, foi determinado pela seguinte expressão
cpar = 28,11 - 0,1967x10-2T+0,4802x10-5T2-1,966x10-9T3
273< T(K)< 1800
Nesta equação cpar vem em [kJ/kmol.K] e T em [K]
•
Determinação da condutibilidade térmica do ar – kar
Para o cálculo da condutibilidade térmica do ar recorreu-se às tabelas termodinâmicas,
Raznjevic (1970). Apresenta-se em baixo a figura que mostra a variação de kar com a
temperatura bem como a função de ajuste respectiva.
0.12
0.10
k (W/mK)
0.08
0.06
0.04
y = -8.97E-09x2 + 6.16E-05x + 2.45E-02
R2 = 9.99E-01
0.02
0.00
0
500
1000
1500
2000
T(ºC)
Figura AIV.11- Variação da condutibilidade térmica com a temperatura para o ar – Ref1
•
Determinação da viscosidade do ar – µar (expressão apresentada no Apêndice I)
Para determinação da viscosidade para o ar recorreu-se à expressão apresentada por
White (1991) que é a seguinte:
32
µ  T  T0 + S
= 
µ0  T0  T + S
210 < T(K) < 1900
em que para o ar se tem: T0 = 273 K; µ0 = 1,716x10-5 Pa.s; S = 111 K
256
(A.I.8)
Apêndice V – Tabelas de dados e resultados experimentais
Apêndice V. Tabelas de dados e resultados experimentais
Neste Apêndice apresentam-se todas as tabelas de dados e resultados experimentais
relativamente a todos os ensaios feitos, com e sem combustão para todas as granulometrias.
As Tabelas de 1 a 5 referem-se aos dados experimentais, de temperaturas do leito, do ar
e da água, do caudal de ar e da pressão do leito. Também se apresenta o valor experimental do
caudal de água e o resultado da respectiva potência térmica. A temperatura da parede é
também registada depois de ser calculada de acordo com o calor recebido pela água e tendo
em atenção o valor do coeficiente de convecção estimado pela equação 4.4 que vem expressa
em termos do número de Nusselt. Todas as variáveis apresentadas referem-se a valores
médios de cada ensaio. Nestas mesmas tabelas são apresentados os valores das temperaturas
corrigidas do lado dos gases devido ao efeito da radiação, e a variação da entalpia do ar
calculada à custa dessas temperaturas.
Nas Tabelas numeradas de 6 a 10 são apresentados os resultados obtidos na primeira
fase do trabalho, sem reacção de queima, no que diz respeito a todos as variáveis envolvidas
na determinação da correlação correspondente à equação 5.17. Mais uma vez, se refere a
temperatura do leito e a temperatura do filme à qual são avaliadas as propriedades do ar,
referidas no Apêndice IV.
Nas Tabelas de 11 a 15 são apresentados também todos os dados experimentais
referidos atrás mas respeitantes aos ensaios com combustão de propano comercial pelo que se
acrescenta o caudal médio de propano usado.
Nas Tabelas numeradas de 16 a 20, são apresentados os resultados correspondentes aos
ensaios com combustão do propano. Também aqui se referem todos as variáveis envolvidas
na determinação da correlação correspondente à equação 7.2, bem como a temperatura do
leito e a do filme à qual são também avaliadas as propriedades da mistura gasosa referidas no
Apêndice IV.
Para a correlação geral apresentada no capítulo 8, correspondente à equação 8.1, foram
usadas todas as variáveis apresentadas nas Tabelas de A.V.6 a A.V.10 , considerando r = 1, e
as variáveis apresentadas nas Tabelas A.V.16 a A.V.20 considerando o valor de r respeitante
a cada ensaio.
257
258
Tabela A.V.1- Dados experimentais obtidos nos ensaios sem combustão e para as partículas com dp=107,5µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qar
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
400
14
0,82
251,6
277
43,9
45
54
73
23,6
24,7
26
90
400
12
1,0
319,9
364
118,1
129
76
73
22,0
25,3
30
330
400
12
1,0
327,2
374
140,6
156
70
140
21,7
23,6
27
304
400
15
1,25
334,3
383
137,2
151
86
73
25,2
29,5
34
365
500
12
0,82
292,5
328
44,8
46
71
73
25,1
26,8
29
148
500
12
1.0
387,8
457
119,8
131
98
140
22,3
24,2
30
404
500
12
1.0
395,0
467
140,2
155
100
35
23,6
32,4
37
356
500
14
1,0
384,0
452
105,4
114
103
73
23,3
28,4
34
428
500
15
1,25
412,3
493
221,9
259
89
73
25,0
33,1
42
680
550
14
0,82
330,2
378
52,5
55
82
73
23,8
25,7
28
158
550
14
1,0
433,6
525
133,9
147
115
73
23,4
30,0
37
549
550
15
1,0
438,4
532
156,6
174
111
35
24,8
36,8
43
486
550
14
1,0
428,0
517
132,9
146
112
140
23,5
26,7
33
512
550
15
1,25
450,1
550
287,3
352
75
73
25,9
36,4
48
885
600
13
0,82
342,3
394
47,2
49
89
73
25,1
27,2
30
178
600
13
1,0
472,5
587
255,2
306
86
140
22,2
26,6
35
711
600
13
1,0
475,2
591
244,9
290
90
73
22,6
30,9
40
706
600
14
1,0
473,1
587
172,5
194
126
73
23,7
31,9
41
693
650
11
0,82
364,6
424
49,5
51
96
73
25,0
27,3
30
195
660
13
1,0
514,7
657
260,4
311
102
35
24,4
47,7
59
947
660
13
1,0
514,5
657
258,3
309
104
73
23,3
34,2
46
922
660
14
1,0
518,3
664
231,3
271
121
73
23,9
34,2
46
877
660
14
1,0
517,8
663
225,2
263
122
73
23,7
34,5
47
912
700
9
0,82
391,1
462
51,6
54
111
73
24,9
27,5
30
217
Tabela A.V.2- Dados experimentais obtidos nos ensaios sem combustão para as partículas com dp=142,5µm
259
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qar
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
400
11
0,82
269,3
299
44,5
46
64
73
23,3
24,5
26
102
400
11
1
269,1
299
75,6
80
67
35
23,3
27,0
29
153
400
13
1
284,0
317
79,3
85
70
140
23,3
24,0
26
128
400
13
1
278,6
310
75,5
80
71
73
23,1
24,8
27
147
400
14
1,25
307,0
347
121,2
133
81
73
23,6
26,2
29
225
400
15
1,5
324,5
370
177,8
202
77
73
24,1
28,1
33
343
500
14
0,82
300,9
339
46,6
48
76
73
24,2
25,6
27
117
500
15
1
350,0
404
102,8
111
88
35
24,8
29,9
33
211
500
15
1
343,2
395
95,0
102
90
73
24,4
26,7
29
193
500
16
1,25
386,0
454
164,3
185
101
73
25,5
29,5
34
341
500
15
1,5
400,7
475
277,8
338
63
73
26,2
33,7
42
632
600
14
0,82
345,8
399
50,1
52
89
73
24,5
26,2
28
138
600
16
1
421,6
507
115,1
125
120
73
24,7
27,9
32
270
600
15
1
429,8
519
141,6
156
113
35
25,5
33,5
38
328
600
15
1,25
461,1
568
261,7
315
98
73
25,7
32,7
41
594
700
14
0,82
395,0
468
59,1
62
105
73
24,6
26,8
29
188
700
15
1
497,7
628
178,0
213
131
35
26,0
37,5
43
468
700
15
1
504,3
640
195,7
224
134
73
25,3
31,1
38
495
260
Tabela A.V.3- Dados experimentais obtidos nos ensaios sem combustão para as partículas com dp=180 µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qar
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
400
10
1
300,6
339
64,9
69
80
73
21,8
23,6
26
151
400
10
1
272,8
304
69,3
73
67
35
21,1
25,2
27
165
400
17
1,25
297,9
335
86,7
93
89
73
21,4
23,4
26
165
400
10
1,5
322,9
368
107,3
117
112
73
21,9
24,7
28
231
500
9
1
362,4
421
74,0
79
84
73
21,5
24,0
27
210
500
11
1
319,6
364
89,6
96
79
35
21,2
26,0
28
196
500
13
1,25
341,5
393
112,0
122
101
73
21,9
24,7
28
234
500
12
1,5
363,2
423
159,2
179
112
73
22,1
25,5
29
295
600
10
0,82
367,1
428
50,6
53
98
73
22,0
24,2
27
181
600
11
1
369,4
431
117,0
128
91
73
21,1
24,6
29
296
600
10
1
365,8
426
118,1
129
89
35
21,6
28,1
31
263
600
10
1
370,1
432
116,3
127
91
140
21,1
22,9
26
289
600
11
1
393,3
465
86,7
93
115
73
21,8
24,9
28
262
600
12
1,25
408,3
487
162,5
183
110
73
22,3
26,0
30
308
700
12
0,82
400,2
475
55,9
59
102
73
22,0
24,4
27
206
700
10
1
414,9
497
160,6
180
95
35
22,2
30,8
35
349
700
11
1
417,1
500
158,6
178
98
73
21,6
26,0
31
370
700
10
1
414,5
497
155,5
174
100
140
21,5
23,7
28
369
700
13
1
429,0
518
110,0
119
129
73
21,9
25,3
29
314
700
13
1,25
475,2
591
221,5
259
122
73
22,5
27,3
33
409
Tabela A.V.4- Dados experimentais obtidos nos ensaios sem combustão para as partículas com dp=282,5 µm
261
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qar
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
400
10
1
300,6
339
66,8
71
82
35
21,3
25,3
27
163
400
10
1
305,9
346
67,8
72
83
73
21,8
24,0
26
185
400
9
1,25
288,9
324
87,4
94
84
73
21,2
23,3
26
195
400
9
1,5
290,6
326
117,8
129
86
73
21,1
24,0
27
243
500
13
0,82
310,5
352
43,7
45
75
73
20,9
22,4
24
131
500
9
1
357,2
414
79,3
84
101
35
21,9
24,7
30
224
500
9
1
354,6
411
75,8
81
104
73
21,4
24,1
27
233
500
15
1,25
347,0
400
109,3
119
106
73
20,9
24,0
28
268
500
15
1,5
350,7
405
151,0
169
110
73
21,0
24,5
28
296
600
15
0,82
352,3
408
48,5
51
89
73
20,5
22,6
25
174
600
8
1
400,3
475
91,5
98
117
35
21,6
28,0
31
257
600
8
1
401,3
477
87,8
94
117
73
21,4
24,9
29
296
600
15
1,25
393,8
466
134,0
148
118
73
20,7
24,3
28
306
600
15
1,5
402,8
479
221,0
258
100
73
21,5
26,1
31
386
700
8
0,82
372,5
436
50,0
52
96
73
20,3
22,4
25
183
700
9
1
433,9
526
103,3
112
126
35
21,8
29,1
33
298
700
9
1
442,7
540
100,7
109
131
73
21,3
25,0
29
309
700
9
1,25
411,2
492
198,8
229
97
73
21,0
25,5
31
382
262
Tabela A.V.5- Dados experimentais obtidos nos ensaios sem combustão para as partículas com dp=357,5 µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qar
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
400
9
1
241,2
265
56,3
59
63
35
20,0
22,6
24
108
400
9
1
259,4
287
58,6
62
69
73
19,7
21,0
22
104
400
12
1,25
313,8
356
84,1
90
101
73
19,4
21,3
23
156
400
14
1,5
296,7
334
109,7
120
98
73
19,9
22,3
25
204
500
14
0,82
315,0
358
44,9
47
79
73
19,2
20,9
23
139
500
9
1
318,4
362
69,1
73
89
35
20,1
24,2
26
167
500
9
1
328,7
376
68,9
73
91
73
19,8
20,3
24
170
500
14
1,25
335,9
385
116,1
127
97
73
19,5
22,6
26
266
500
15
1,5
327,9
375
176,4
200
83
73
20,2
23,8
28
307
600
12
0,82
347,8
402
47,7
50
88
73
18,7
20,7
23
174
600
9
1
385,0
453
83,5
89
111
35
20,4
25,9
29
224
600
8
1
388,1
458
80,6
86
113
73
20,4
23,2
26
239
600
12
1,25
374,9
439
170,0
192
94
73
19,0
22,9
27
330
600
12
1,5
363,1
422
224,3
263
69
73
19,6
24,0
29
375
700
12
0,82
390,8
462
54,5
57
101
73
19,0
21,4
24
208
700
8
1
435,7
529
95,1
102
135
35
20,7
27,4
31
272
700
8
1
436,6
530
91,0
98
136
73
20,2
23,5
27
274
700
12
1,25
403,7
480
217,0
253
84
73
19,2
23,7
29
387
700
12
1,5
391,5
463
284,8
349
49
73
19,7
25,6
32
495
Tabela A.V.6- Resultados experimentais das variáveis usadas na correlaçâo 5.17 para as partículas com dp=107,5 µm
Ap = 0,1421 m2 ; dp/di = 0.001972
263
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
DTadim
400
400
400
400
500
500
500
500
500
550
550
550
550
550
600
600
600
600
650
660
660
660
660
700
124,25
147,25
152,5
154,75
151
172,75
182,25
170,5
210,75
165,25
192,75
202,5
190,5
249,5
177,25
244
242,5
219
190,25
272,25
265,25
255,75
254,25
203,5
0,82
1
1
1,25
0,82
1
1
1
1,25
0,82
1
1
1
1,25
0,82
1
1
1
0,82
1
1
1
1
0,82
90
330
304
365
148
404
356
428
680
158
549
486
512
885
178
711
706
693
195
947
922
877
912
217
119,13
205,55
229,81
218,33
136,68
239,98
252,37
219,05
322,64
167,13
261,72
277,84
265,67
394,76
162,00
400,16
384,39
313,34
176,95
401,53
413,99
387,49
380,60
194,04
5,32
11,30
9,31
11,76
7,62
11,85
9,93
13,75
14,83
6,65
14,76
12,31
13,56
15,78
7,73
12,50
12,92
15,56
7,75
16,60
15,67
15,93
16,86
7,87
9,04
18,43
15,04
18,94
12,35
18,49
15,25
21,55
21,78
10,52
22,30
18,31
20,56
21,85
11,98
17,46
18,09
22,56
11,76
22,26
21,22
21,86
23,20
11,69
233,77
273,86
271,47
338,07
223,16
262,74
258,90
263,67
310,33
218,02
254,84
251,22
255,70
294,48
213,94
237,27
237,74
245,41
209,75
228,93
230,92
233,70
234,15
205,70
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
18
22
22
27
23
28
27
28
35
25
30
30
30
38
28
34
34
34
31
37
37
37
37
33
0,052
0,311
0,424
0,385
0,037
0,242
0,294
0,188
0,642
0,053
0,241
0,299
0,247
0,930
0,034
0,653
0,591
0,320
0,034
0,544
0,559
0,456
0,434
0,036
264
Tabela A.V.7- Resultados experimentais das variáveis usadas na correlaçâo 5.17 para as partículas com dp=142,5 µm
AP = 0,1421 m2 ; dp/di = 0,002615
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
DTadim
400
124,5
0,82
102
120,88
5,94
10,09
233,66
0,73
9
0,055
400
134,5
1
153
161,26
6,68
11,14
279,93
0,73
10
0,148
400
134,25
1
128
170,57
5,28
8,82
280,05
0,73
10
0,172
400
133,5
1
147
163,99
6,31
10,54
280,42
0,73
10
0,153
400
147,75
1,25
225
209,94
7,54
12,29
342,04
0,73
13
0,329
400
167
1,5
343
255,33
9,45
14,90
397,71
0,73
16
0,617
500
150,5
0,82
117
145,12
5,67
9,20
223,35
0,73
11
0,045
500
169,25
1
211
217,36
6,83
10,73
264,19
0,73
13
0,183
500
165
1
193
213,47
6,36
10,06
265,99
0,73
13
0,168
500
188,25
1,25
341
279,53
8,58
13,06
320,70
0,73
16
0,392
500
230,5
1,5
632
371,13
11,98
17,07
362,35
0,73
20
1,039
600
177
0,82
138
172,81
5,62
8,71
214,02
0,73
13
0,043
600
197,25
1
270
262,50
7,24
10,86
253,15
0,73
16
0,179
600
208
1
328
284,47
8,11
11,96
249,24
0,73
16
0,236
600
249,25
1,25
594
399,71
10,46
14,49
294,57
0,73
20
0,674
700
205
0,82
188
211,80
6,25
9,25
205,26
0,73
15
0,050
700
249,75
1
468
360,24
9,14
12,66
235,50
0,73
19
0,299
700
250
1
495
374,95
9,29
12,86
235,43
0,73
19
0,330
Tabela A.V.8- Resultados experimentais das variáveis usadas na correlaçâo 5.17 para as partículas com dp=180 µm
AP = 0,1421 m2 ; dp/di = 0,003303
265
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
DTadim
400
400
400
400
500
500
500
500
600
600
600
600
600
600
700
700
700
700
700
700
130,25
131,75
136,25
143,25
158,25
163
169,5
184,25
176,75
196,5
197,75
194,75
187,25
210,75
203,25
237,5
235
232,5
219,25
256,25
1
1
1,25
1,5
1
1
1,25
1,5
0,82
1
1
1
1
1,25
0,82
1
1
1
1
1,25
151
165
165
231
210
196
234
295
181
296
263
289
262
308
206
349
370
369
314
409
153,02
156,24
178,53
197,87
190,68
208,52
234,25
280,54
176,86
269,36
267,78
272,23
233,13
317,06
210,44
341,42
344,47
344,54
289,20
407,48
6,94
7,43
6,50
8,22
7,75
6,61
7,03
7,40
7,20
7,73
6,91
7,47
7,91
6,84
6,89
7,19
7,56
7,54
7,64
7,06
11,68
12,46
10,82
13,49
12,40
10,50
11,03
11,33
11,17
11,61
10,36
11,25
12,05
10,04
10,23
10,14
10,70
10,70
11,07
9,69
282,04
281,29
348,84
413,59
268,91
266,85
330,11
387,18
214,11
253,43
252,97
254,09
256,95
310,33
205,78
239,31
240,11
240,92
245,32
291,94
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
0,73
11
11
13
16
13
13
17
20
13
16
16
16
16
21
16
19
19
19
19
24
0,122
0,132
0,197
0,273
0,116
0,156
0,222
0,383
0,046
0,190
0,189
0,194
0,121
0,313
0,049
0,246
0,248
0,245
0,144
0,414
266
Tabela A.V.9- Resultados experimentais das variáveis usadas na correlaçâo 5.17 para as partículas com dp=282,5 µm
AP = 0,1421 m2 ; dp/di = 0,005183
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
DTadim
400
131,25
1
163
153,93
7,45
12,51
281,54
0,73
3
0,126
400
131
1
185
156,52
8,32
13,97
281,66
0,73
3
0,131
400
136,5
1,25
195
179,50
7,64
12,71
348,69
0,73
4
0,201
400
145,75
1,5
243
209,01
8,18
13,38
411,84
0,73
5
0,319
500
148,25
0,82
131
145,79
6,32
10,30
224,19
0,73
3
0,045
500
161
1
224
192,26
8,20
13,06
267,71
0,73
4
0,122
500
158,75
1
233
193,08
8,49
13,58
268,69
0,73
4
0,121
500
168,75
1,25
268
231,45
8,15
12,81
330,50
0,73
5
0,214
500
181,25
1,5
296
273,96
7,60
11,70
388,95
0,73
6
0,355
600
175,25
0,82
174
177,31
6,91
10,74
214,61
0,73
4
0,046
600
190
1
257
234,67
7,71
11,69
255,89
0,73
5
0,125
600
188
1
296
232,86
8,94
13,62
256,66
0,73
5
0,121
600
201
1,25
306
289,44
7,44
11,09
314,71
0,73
6
0,235
600
230
1,5
386
372,17
7,30
10,40
362,60
0,73
8
0,509
700
200,5
0,82
183
201,31
6,40
9,54
206,60
0,73
5
0,041
700
219,5
1
298
275,62
7,61
11,02
245,24
0,73
6
0,126
700
216,75
1
309
277,89
7,82
11,38
246,18
0,73
6
0,127
700
247,75
1,25
382
386,85
6,95
9,65
295,14
0,73
8
0,351
Tabela A.V.10- Resultados experimentais das variáveis usadas na correlaçâo 5.17para as partículas com dp=357,5 µm
AP= 0,1421 m2 ; dp/di = 0,00656
267
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
DTadim
400
126,75
1
108
143,62
5,29
8,96
283,80
0,73
2
0,098
400
126,5
1
104
150,49
4,86
8,23
283,93
0,73
2
0,112
400
134
1,25
156
179,44
6,12
10,22
350,22
0,73
3
0,196
400
142,5
1,5
204
203,93
7,04
11,58
414,12
0,73
3
0,292
500
148,25
0,82
139
151,53
6,45
10,51
224,19
0,73
2
0,052
500
156,25
1
167
184,76
6,36
10,21
269,79
0,73
3
0,104
500
155,25
1
170
187,81
6,37
10,24
270,24
0,73
3
0,109
500
169,75
1,25
266
241,25
7,76
12,17
329,98
0,73
4
0,240
500
189
1,5
307
297,18
7,27
11,05
384,41
0,73
4
0,453
600
174
0,82
174
179,62
6,82
10,62
215,03
0,73
3
0,048
600
186,75
1
224
226,80
6,95
10,60
257,14
0,73
3
0,111
600
184,5
1
239
227,61
7,39
11,31
258,02
0,73
3
0,110
600
211,5
1,25
330
327,73
7,09
10,39
310,00
0,73
4
0,340
600
230,25
1,5
375
377,77
6,99
9,95
362,48
0,73
5
0,527
700
201,25
0,82
208
212,94
6,87
10,24
206,37
0,73
3
0,050
700
216
1
272
266,59
7,18
10,46
246,44
0,73
4
0,112
700
213
1
274
267,67
7,20
10,54
247,48
0,73
4
0,111
700
252,75
1,25
387
407,43
6,68
9,22
293,25
0,73
5
0,406
700
278,25
1,5
495
470,90
7,40
9,84
340,89
0,73
6
0,644
268
Tabela A.V.11- Dados experimentais obtidos nos ensaios com combustão e para as partículas com dp=107,5 µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
mpro
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qgas
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
722
9,0
0,85
0,095
560,5
741
93,7
100
219
73
25,4
324
40
597
719
4,4
1,0
0,1
571,8
762
238,3
281
192
73
26,7
39,0
53
1043
723
18
0,85
0,09
574,2
767
95,9
102
226
73
25,3
32,9
41
618
709
11
1,0
0,09
602.7
822
300,0
370
179
73
27,0
42,7
60
1300
715
14
0,98
0,1
586,7
790
300,9
371
165
35
27,2
51,9
64
1003
728
9
0,83
0,09
571,7
761
107,1
116
216
73
19,7
27,2
36
630
729
12
0,82
0,098
537,4
699
68,7
73
210
73
18,7
24,1
30
458
720
9,5
0,9
0,098
580,1
778
140,7
155
226
73
19,3
29,3
40
853
725
10
0,83
0,099
566,4
752
100,1
108
218
73
18,7
26,3
35
642
Tabela A.V.12- Dados experimentais obtidos nos ensaios com combustão para as partículas com dp=142,5 µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
mpro
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qgas
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
717
10
1,0
0,1
585,9
789
224,3
262
210
73
25,2
35,1
46
843
714
11
0,97
0,1
584,3
786
204,0
234
215
35
26,8
46,5
56
800
719
15
0,83
0,09
543,9
710
89,2
95
206
35
24,0
34,5
40
424
712
11
0,83
0,1
582,8
783
174,4
195
231
35
25,9
45,7
56
806
718
14
0,84
0,09
514,8
658
73,7
77
196
35
24,3
33,0
37
252
713
11
0,98
0,09
598,1
813
173,5
194
240
35
26,3
45,7
58
786
732
16
0,83
0,10
537,6
699
80,9
86
206
73
18,9
23,9
30
429
720
13
0,98
0,098
603,6
825
216,8
252
224
73
19,8
29,9
41
857
Tabela A.V.13- Dados experimentais obtidos nos ensaios com combustão para as partículas com dp=180 µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
mpro
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qgas
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
791
738
777
727
786
748
770
737
720
724
718
9
7
12
7
8
4
7
5
9
9
7
1,0
1,2
1,0
1,2
1,0
1,2
1,0
1,0
1,0
1,2
1,2
0,1
0,12
0,096
0,12
0,098
0,13
0,11
0,12
0,12
0,12
0,12
554,8
581,5
547,7
592,2
581,1
581,3
550,1
494,7
600,0
600,5
607,0
730
781
717
802
780
780
722
624
818
819
832
107,8
192,3
105,2
181,8
122,3
192,0
117,0
124,7
132,8
196,5
213,5
117
219
114
206
133
219
128
136
146
225
247
242
270
236
295
263
264
243
202
275
276
284
73
73
73
73
73
73
73
73
73
73
73
21,4
21,9
22,0
22,6
22,3
23,2
19,7
19,8
21,0
21,6
21,8
27,1
31,5
27,4
31,8
26,9
31,4
25,6
28,1
28,4
31,4
31,8
33
42
33
42
36
41
32
37
37
42
43
480
813
457
766
560
698
497
703
628
827
850
Tabela A.V.14- Dados experimentais obtidos nos ensaios com combustão para as partículas com dp=282,5 µm
269
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
mpro
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qgas
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
805
763
793
735
804
781
731
811
778
783
743
723
775
745
9
8
10
10
9
9
9
9
9
10
10
10
9
9
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1.2
1,2
0,12
0,12
0,12
0,12
0,095
0,095
0,095
0,1
0,1
0,12
0,13
0,14
0,12
0,12
469,5
322,8
447,5
321,2
409,3
288,7
336,5
470,7
307,9
469,0
342,1
414,5
571,8
434,4
583
367
548
354
491
323
385
585
348
582
393
496
764
527
104,6
137,4
95,9
142,2
94,7
118,2
121,2
102,9
125,8
102,4
134,4
166,3
160,8
183,4
113
150
103
155
102
127
131
111
137
110
147
186
180
207
197
87
181
81
155
76
101
189
85
194
103
163
284
162
73
73
73
73
73
73
73
73
73
73
73
73
140
140
19,9
21,9
20,1
21,9
20,7
21,9
22,1
20,1
21,1
21,4
22,8
23,3
24,0
24,8
26,3
36,7
26,8
38,4
26,9
34,7
36,4
26,3
33,1
27,8
36,2
35,9
29,7
33,1
33
55
34
57
34
49
52
33
47
35
51
50
41
50
539
1320
571
1397
531
1084
1210
525
1020
537
1134
1064
922
1353
270
Tabela A.V.15- Dados experimentais obtidos nos ensaios com combustão para as partículas com dp=357,5 µm
corr
corr
TL
(ºC)
PL
(cm)
mar
(kg/h)
mpro
(kg/h)
Tge
(ºC)
Tge
(ºC)
Tgs
(ºC)
Tgs
(ºC)
qgas
(W)
mag
(kg/h)
Tage
(ºC)
Tags
(ºC)
Tw
(ºC)
qag
(W)
765
9
1,0
0,11
461,1
570
96,6
104
195
73
20,1
26,8
34
566
750
9
1,0
0,1
332,3
379
128,2
139
98
73
21,4
36,5
53
1276
818
9
1,0
0,1
437,9
534
105,2
114
168
73
19,9
26,5
34
560
720
9
1,0
0,1
286,4
319
154,3
169
59
73
23,6
42,6
64
1607
825
9
1,2
0,12
470,0
585
141,2
157
199
73
20,8
28,2
36
625
785
9
1,2
0,12
314,2
355
162,0
179
81
73
23,9
40,0
58
1366
784
13
1.0
0,1
475,9
594
109,5
118
191
73
20,1
28,2
37
682
717
13
1,0
0,1
376,8
441
131,5
143
122
73
21,7
37,9
56
1367
779
10
1,0
0,1
502,8
640
118,8
130
208
73
19,9
25,9
33
508
721
10
1,0
0,1
301,9
339
155,6
172
66
73
22,1
37,9
56
1343
790
15
1,2
0,12
559,6
742
174,8
198
266
73
20,7
28,6
38
672
732
15
1,2
0,12
431,8
522
196,8
224
144
73
23,6
39,6
58
1356
806
11
1,0
0,12
458,2
565
103,1
111
189
73
19,2
25,6
33
539
754
11
1,0
0,11
315,1
357
160,4
178
74
73
22,2
38,8
58
1407
809
13
1,0
0,11
476,1
593
101,2
109
198
73
19,3
25,0
31
481
752
13
1,0
0,1
308,3
348
155,2
171
72
73
22,6
39,8
59
1460
836
11
1,25
0,11
509,5
650
151,6
169
234
73
21,2
28,3
36
607
769
11
1,25
0,11
326,8
372
177,4
199
84
73
24,4
41,0
59
1408
Tabela A.V.16- Resultados experimentais das variáveis usadas na correlaçâo 7.2 para as partículas com dp=107,5 µm
AP = 0,1421 m2 ; dp/di = 0,001972
271
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
mpro
(kg/h)
r
qag
(W
DtlnL-W
(ºC)
hglo
2
(W/m ºC
Nuexp
Re
Pr
vo/vmf
Ln(dTadim)
722
225,50
0,85
0,095
1,75
597
255,89
16,42
22,77
265,48
0,74
35
0,092
719
276,50
1
0,1
1,56
1043
408,60
17,96
22,56
284,40
0,74
40
0,419
723
226,75
0,85
0,09
1,66
618
257,23
16,91
23,44
264,07
0,74
35
0,094
709
299,75
1
0,09
1,41
1300
458,81
19,94
25,06
281,81
0,74
40
0,649
715
303,50
0,98
0,1
1,60
1003
457,65
15,42
19,37
279,23
0,74
40
0,638
728
229,00
0,83
0,09
1,70
630
283,65
15,63
21,67
258,46
0,74
34
0,123
729
215,50
0,82
0,098
1,87
458
235,26
13,70
19,00
257,89
0,74
34
0,063
720
238,75
0,9
0,098
1,70
853
317,92
18,88
26,18
280,37
0,74
37
0,185
725
225,75
0,83
0,1
1,88
642
274,68
16,45
22,81
261,27
0,74
34
0,112
272
Tabela A.V.17- Resultados experimentais das variáveis usadas na correlaçâo 7.2 para as partículas com dp=142,5 µm
AP = 0,1421 m2 ; dp/di = 0,002615
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
mpro
(kg/h)
r
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
Ln(dTadim)
717
267,75
1
0,1
1,56
843
401,41
14,78
19,36
294,98
0,74
19
0,388
714
265,00
0,97
0,1
1,61
800
367,13
15,33
20,09
286,93
0,74
18
0,315
719
223,50
0,83
0,09
1,70
424
248,28
12,02
16,66
258,46
0,74
16
0,084
712
254,75
0,98
0,1
1,60
806
333,19
17,02
22,30
289,61
0,74
18
0,238
718
217,25
0,84
0,09
1,68
352
226,13
10,95
15,19
261,27
0,74
16
0,061
713
255,75
0,98
0,09
1,44
786
330,16
16,75
21,95
286,93
0,74
18
0,233
732
219,50
0,83
0,1
1,88
429
255,48
11,82
16,39
261,27
0,74
16
0,083
720
263,50
0,98
0,098
1,56
857
400,42
15,06
19,73
289,08
0,74
19
0,372
Tabela A.V.18- Resultados experimentais das variáveis usadas na correlaçâo 7.2 para as partículas com dp=180 µm
AP = 0,1421 m2 ; dp/di = 0,003303
273
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
mpro
(kg/h)
r
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
Ln(dTadim)
791
243,50
1
0,1
1,56
480
306,38
11,02
14,44
294,98
0,74
22
0,117
738
260,25
1,2
0,13
1,69
813
379,05
15,09
19,77
356,65
0,74
24
0,293
777
239,25
1
0,096
1,50
457
298,97
10,76
14,09
293,90
0,74
21
0,115
727
254,25
1,2
0,12
1,56
766
364,45
14,79
19,38
353,97
0,74
25
0,274
786
247,75
1
0,098
1,53
560
319,26
12,34
16,17
294,44
0,74
23
0,138
748
262,25
1,2
0,13
1,69
698
383,54
12,81
16,78
356,65
0,74
24
0,290
770
240,50
1
0,11
1,72
497
314,77
11,11
14,56
297,66
0,74
22
0,139
737
236,75
1
0,12
1,88
703
307,27
16,10
21,09
300,34
0,74
21
0,152
720
235,00
1
0,12
1,88
628
312,78
14,13
18,51
300,34
0,74
20
0,174
724
258,25
1,2
0,12
1,56
827
379,31
15,34
20,10
353,97
0,74
23
0,312
718
262,75
1,2
0,12
1,56
850
393,62
15,20
19,91
353,97
0,74
23
0,360
274
Tabela A.V.19- Resultados experimentais das variáveis usadas na correlaçâo 7.2 para as partículas com dp=282,5 µm
AP = 0,1421 m2 ; dp/di = 0,005183
1
exp
TL
(ºC)
Tf
(ºC)
mar
(kg/h)
mpro
(kg/h)
r
qag
(W
DtlnL-W
(ºC)
hglo
2
(W/m ºC
Nuexp
Re
Pr
805
246,00
1
0,12
1,88
539
305,25
12,43
16,28
300,34
0,74
7
0,109
763
255,75
1
0,12
1,88
1320
305,19
30,44
39,87 *
300,34
0,74
7
0,144
793
241,00
1
0,12
1,88
571
287,75
13,96
18,29
300,34
0,74
8
0,095
735
251,00
1
0,12
1,88
1397
299,87
32,78
42,95 *
300,34
0,74
8
0,156
804
243,50
1
0,095
1,49
531
289,26
12,92
16,92
293,64
0,74
7
0,092
781
251,50
1
0,095
1,49
1084
292,09
26,12
34,21 *
293,64
0,74
7
0,113
731
241,50
1
0,095
1,49
1210
278,92
30,53
39,99 *
293,64
0,74
6
0,124
811
247,00
1
0,1
1,56
525
304,35
12,14
15,90
294,98
0,74
7
0,106
778
252,25
1
0,1
1,56
1020
306,02
23,45
30,73 *
294,98
0,74
7
0,131
783
240,75
1
0,12
1,88
537
292,62
12,91
16,92
300,34
0,74
7
0,106
743
248,00
1
0,13
2,03
1134
301,74
26,45
34,65 *
303,02
0,74
7
0,149
723
252,25
1,3
0,14
1,68
1064
335,82
22,30
29,21 *
1
386,15
0,74
8
0,226
vo/vmf Ln(dTadim)
Os pontos assinalados com * não foram incluídos na correlação final porque como já foi explicado correspondem a uma fase diferente de combustão.
Tabela A.V.20- Resultados experimentais das variáveis usadas na correlaçâo 7.2 para as partículas com dp=357,5 µm
AP = 0,1421 m2 ; dp/di = 0,00656
Tf
(ºC)
mar
(kg/h)
mpro
(kg/h)
r
qag
(W)
DtlnL-W
(ºC)
hglo
2
(W/m ºC)
Nuexp
Re
Pr
vo/vmf
Ln(dTadim)
765
750
234,25
248,75
1
1
0,11
0,1
1,72
1,56
566
1276
281,77
292,00
14,14
30,75
18,52
40,28 *
297,66
294,98
0,74
0,74
4
4
0,101
0,132
818
250,00
1
0,1
1,56
560
308,45
12,78
16,74
294,98
0,74
5
0,108
720
254,25
1
0,1
1,56
1607
300,73
37,60
49,26 *
294,98
0,74
4
0,174
825
263,50
1,2
0,12
1,56
625
356,27
12,34
16,17
353,97
0,74
6
0,166
785
270,00
1,2
0,12
1,56
1366
337,96
28,44
37,26 *
353,97
0,74
5
0,182
784
244,00
1
0,1
1,56
682
299,78
16,01
20,97
294,98
0,74
5
0,115
717
243,00
1
0,1
1,56
1367
283,06
33,98
44,52 *
294,98
0,74
4
0,141
779
243,75
1
0,1
1,56
508
318,13
11,24
14,72
294,98
0,74
5
0,139
721
251,25
1
0,11
1,72
1343
314,40
30,06
39,38 *
297,66
0,74
4
0,192
790
266,00
1,2
0,12
1,56
672
382,54
12,36
16,19
353,97
0,74
6
0,239
732
268,00
1,2
0,12
1,56
1356
362,54
26,32
34,48 *
353,97
0,74
5
0,283
806
245,75
1
0,12
1,88
539
303,02
12,52
16,40
300,34
0,74
5
0,106
754
262,00
1
0,11
1,72
1407
327,67
30,22
39,59 *
297,66
0,74
5
0,189
809
245,00
1
0,11
1,72
481
304,35
11,12
14,57
297,66
0,74
5
0,106
752
260,25
1
0,1
1,56
1460
318,79
32,23
42,22 *
294,98
0,74
4
0,176
836
269,25
1,2
0,11
1,43
607
371,74
11,49
15,05
351,29
0,74
6
0,182
351,29
0,74
6
0,220
769
2
exp
TL
(ºC)
271,50
1,2
0,11
1,43
1408
351,07
28,22
36,97 *
2
Os pontos assinalados com * não foram incluídos na correlação final 7.2 porque como já foi explicado correspondem a uma fase diferente de combustão.
275