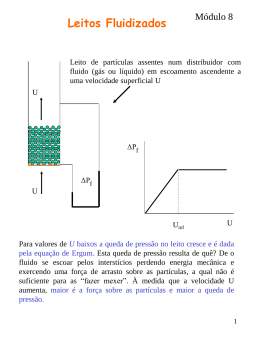
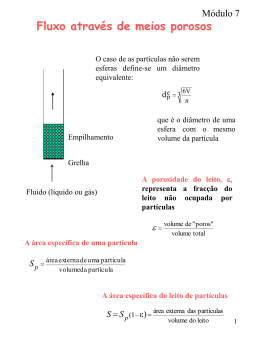
TA 631 – OPERAÇÕES UNITÁRIAS I
Aula 20: 01/06/2012
Escoamento em leitos porosos
•
•
•
•
•
•
Lei de Darcy
Porosidade, Diâmetro equivalente
Equação de Blake-Kozeny
Equação de Burke-Plummer
Equação de Ergun
Leitos fixos e fluidizados
1
1. Lei de Darcy
Henry Darcy em 1856 demonstrou que a
velocidade média (v) de um fluido newtoniano
quando escoa em regime laminar dentro de um leito
poroso é proporcional ao gradiente de pressão e
inversamente proporcional à distância percorrida.
(P)
v f leito  K
L
v = velocidade média do fluido no leito poroso
K = constante que depende das propriedades
do fluído e do leito poroso
(-P) = queda de pressão através do leito
L = percurso realizado no leito poroso
2
A equação de Darcy também pode ser escrita
da seguinte maneira:
(P)
v f leito  B
f L
B = coeficiente de permeabilidade,
que depende apenas das
propriedades físicas do leito poroso
μf = viscosidade do fluído.
3
2. Equação de Poiseuille
Explica o escoamento em regime laminar de um
fluido newtoniano dentro de um tubo.
 P 32 v
 2
L
D
Onde:
∆p é a o gradiente de pressão (N/m2)
v é a velocidade do fluido no tubo (m/s)
D é o diâmetro do tubo (m)
L é o comprimento do tubo (m)
µ é a viscosidade do fluido (Pa.s)
D (P)
v
32  L
2
Colocando a equação em termos da
velocidade média do fluido no tubo:
4
Comparando as equações:
Poiseuille
Darcy modificada
(P)
D (P)
v canal  B

32  L
L
tortuoso
2
vno tubo
Considerando o “canal tortuoso” como um tubo, relaciona-se as duas
equações e obtém-se uma expressão para “B” :
D2
B   k D2
32
k = f(, Dp, Φp, etc.)
Logo, é necessário uma equação “mais robusta”.
5
3. Dedução de um modelo para descrever a
passagem de um fluido em um leito particulado
Quais são as variáveis que atuam no escoamento de um
fluido newtoniano em um leito de partículas sólidas rígidas?
Precisamos de uma equação
para descrever como varia a
velocidade do fluido com a
pressão aplicada, a distância
percorrida (altura do leito),
a viscosidade e a densidade do
fluido, o diâmetro das partículas
e sua esfericidade, a porosidade
do leito.
Primeiro para leitos fixos e
(P)
v canal  f (
,  ,  , Dp ,  p ,  ) depois em leitos móveis
L
tortuoso
(ou fluidizados)
6
Considerações para as equações que
serão desenvolvidas a seguir:
• Fluido Newtoniano
• As partículas se distribuem de forma homogênea,
o que permite a formação de canais de
escoamento contínuos, uniformes e em paralelo
• Um leito de percurso curto (L pequeno)
7
3.1. Porosidade
Lembrando que em um leito poroso existem espaços vazios
(zonas sem partículas).
A porosidade () é definida como
a razão entre o volume do leito que
não está ocupado com material sólido
e o volume total do leito.
Volume vazio
ε
Volume total do leito
v0
8
Volume vazio

Volume totaldo leito
v0
No caso do fluxo através do
leito de partículas:
s = densidade da partícula sólida
f = densidade do fluido
Fração
Vazio
Sólido
ε
(1 ε)
Volume
ε (SL b )
(1  ε) (SL b )
Massa
m  V 
ε (SL b )ρf
(1 ε) (SL b )ρs
9
Equação pra correlacionar a porosidade com as
densidades do leito, das partículas e do fluido:
mtotal
 leito 
Vtotal
(densidade aparente)
massa total = massa de sólidos + massa de fluido
mtotal  (1  ε) (SL b ) s  ε (SL b )f
Vtotal  SL b
Substituindo os termos, tem-se:
leito  (1   ) s   f
leito  s   ( f  s )
v0
leito   s

 f  s
[1]
10
3.2. Volumes no leito
SLb  volume total do leito
 SLb  volume disponível para o fluxo(volume de vazios)
(1   )SLb  volume ocupado pelas particulas sólidas
Volume
total do
leito
Conjunto de partículas
Volume = soma dos
volumes unitários
Leito
particulado
Volume
total de
vazios
Volume
total de
sólidos
11
3.3. Relação entre “velocidade superficial” (fora do leito)
do fluido e velocidade média do fluido no leito
A vazão mássica do fluido fora do leito
é igual a vazão dentro do leito:
Balanço de
massa


m fora  mleito


 f Q fora   f Q leito
 f v0 S   f vleito S 
v0  vleito [2]
Quando o leito não tem partículas:
Se a porosidade for 50%:
v0
Área de
vazios
 1
  0,5
vleito  v0
vleito  2  v0
12
3.4. Diâmetro equivalente
Como não se trata do escoamento em
uma tubulação cilíndrica (pois tem-se
um canal tortuoso), devemos usar o
conceito de diâmetro equivalente e de
raio hidráulico, cuja definição é:
 área transversal de fluxo

Deq  4 RH  4  
 perimetro molhado

v0
Multiplicando por (Lb/Lb) tem-se:


volume disponível para o fluxo do fluido

Deq  4  
 área de atrito entre o fluido e as partículas sólidas 
A área de atrito entre o fluido e as partículas sólida
corresponde a área externa das partículas sólidas.
13


volume disponível para o fluxo do fluido

Deq  4  
 área de atrito entre o fluido e as partículas sólidas 
Sabemos que:
 SLb  volume disponível para fluxo(volume de vazios)
(1   )SLb  volume ocupado pelas particulas sólidas
Se as é a área superficial por unidade de volume sólido:
no de partículas área externa de uma partícula sólida
as  o

n de partículas
volume de uma partícula sólida
Área de atrito = volume ocupado pelas partículas sólidas x as
Substituindo essas relações no “Deq” acima tem-se:


 SLb

Deq  4  
 1    SLb as 
 


Deq  4  
 1    as 
14
 


Deq  4  
 1    as 
Para partículas esféricas tem-se:
área superficial do sólido
as 
volume do sólido
D
6
as 

 3 Dp
D
2
p
6
4  
 D p
Deq  
6  1    
p
[3]
15
3.5. Leito particulado fixo
A perda de pressão no leito particulado
é obtida com o Balanço de Energia:
^
Ef
P1
v12 Wˆ
P2
v22
 z1 
 
 z2 

f g
2g g  f g
2g g
v0
 L
 E f  2 fF 
D
f
 eq.canal
P
^

2
vleito


[4]
Substituindo fF para fluido Newtoniano em regime laminar tem-se:
16
16
fF 

Re Deq.canal vleito  f
f
P
f

32Lvleito f
D
eq.canal

[5]
2
f
16
P
f

1
2 ( P)
[6]
vleito  Deq.canal 
32
f L
32Lvleito f
D
eq.canal

2
v0  vleito
f
[2]
4  
 D p [3]
Deq  
6  1    
Substituindo [3] e [6] em [2], obtém-se:
Equações [7] e [8]
válidas para
partículas
esféricas, fluido
Newtoniano em
regime laminar.

(P)
v0 
2
72 (1   )  f L
D
2
p
3
[7]
ou
72  f Lvo 1   2
P 
[8]
2
3
Dp

17
Regimes de escoamento
Número de Reynolds
4  
 D p
Deq  
6  1    
 f .v f leito.Deq.canal
Re 
f
v0  vleito
Substituindo Deq [3] e vleito [2] em Re tem-se:
4 Dp v0  f
Re 
6 (1   )  f
[9]
Definição do regime do fluxo de fluido:
 Laminar quando Re < 10
 Turbulento quando Re > 100
18
3.5.1. Regime Laminar
72  Lvo 1   
P 
2
3
Dp

2
De [8]
Os dados experimentais revelam que o valor da
constante (72) em [8] geralmente é maior, como
mostra a equação abaixo:
Equação de Blake-Kozeny;
válida para <0,5 e Re<10
150  Lv0 1   
P 
2
3
Dp

2
19
Laminar
Fator de Fanning
k1
fF 
Re
Turbulento
f F  k2
Re
20
3.5.2. Regime Turbulento
Para o regime turbulento pode propor-se:
fF  k
Agora, substituindo [2] e [3] em [4] tem-se:
v0  vleito
[2]
4  
 D p [3]
Deq  
6  1    
 L
 E f  2 fF 
D
f
 eq.canal
P
^
P 
Equação de
Burke-Plummer
(k=0,583)

vleito2
[4]


3 k  f v02 L 1   
Dp
3
1,75 f v L 1    [10]
P 
3
Dp

2
0
21
Somando os dois regimes (laminar de Blake-Kozeny e turbulento de
a equação geral de Ergun
Burke-Plummer ), tem-se
que descreve a queda de pressão de um fluido deslocando-se em
um leito poroso fixo:
150 f v0 L 1   2 1,75 f v02 L 1    [11]
P 

2
3
3
Dp

Dp

Rearranjando tem-se:
P Dp 
150


1
,
75
2
 f v0 L 1    Re
3
[12]
22
3.6. Partículas não esféricas
A equação de Ergun [11] inclui a esfericidade quando as
partículas não são esféricas. Para isso, o diâmetro da
partícula é multiplicado pela esfericidade (phi):
150 f v0 L 1   2 1,75 f v02 L 1   
P 

[13]
2
2
3
3
 p Dp

 p Dp

23
4. Resposta ao fluxo superficial (velocidade v0 do fluido)
Baixa velocidade
O fluido não possui uma força de arraste suficiente para se sobrepor a força
da gravidade e fazer com que as partículas se movimentem: Leito fixo.
Alta Velocidade
Se o fluido tem alta força cinética, as forças de arraste e empuxo superam
a da gravidade e o leito se expande e se movimenta: Leito fluidizado.
P e o aumento da velocidade
superficial v0
Enquanto se estabelece a fluidização
o P cresce, depois se mantém constante.
Comprimento do leito quando
aumenta v0
A altura (L) é constante até que se
atinge o estado de fluidização depois
começa a crescer.
24
5. Fluidização
A fluidização ocorre quando
um fluxo ascendente de
fluido escoa através de um
leito de partículas e adquire
velocidade suficiente para
manter as partículas em
suspensão, sem que sejam
L2
2
L1
1
Sem fluxo
Com fluxo
arrastadas junto com o
fluido.
http://www.youtube.com/watch?feature=fvwp&NR=1&v=3_ILu2Ye8gQ
http://www.youtube.com/watch?v=e5u9oW-PSy0&feature=related
25
A fluidização
é empregada
em:
• Secagem
• Mistura
• Revestimento de
•
•
•
•
•
partículas
Aglomeração de pós
Aquecimento e
resfriamento de sólidos
Congelamento
Torrefação de café
Pirólise
Vantagens da Fluidização:
 Alta mistura dos sólidos (homogeneização rápida)
 A área superficial das partículas sólidas fica completamente
disponível para transferência de calor e de massa
26
5.1. Etapas da fluidização
OA: Aumento da velocidade e da queda de pressão do fluído;
AB: O leito está iniciando a fluidização;
BC: Com o aumento da velocidade, há uma queda leve da
pressão devido à mudança repentina da porosidade do leito;
CD: O log(-∆P) varia linearmente com log(v) até o ponto D.
D∞: Após o ponto D, as partículas começam a ser carregadas pelo
fluído e perde-se a funcionalidade do sistema.
Transporte
pneumático
Leito fluidizado
vmf = velocidade
mínima de
fluidização
Leito fixo
va = velocidade
de arraste
27
Exemplo da aplicação de fluidização em resfriamento de sólidos
Saída de ar
Entrada de sólidos quentes
Água quente
Água fria
Entrada
de ar
Leito
fluidizado
distribuidor
Entrada
de ar
Saída de
sólidos frios
http://www.youtube.com/watch?v=CGXr_GKhksE&feature=related
28
5.2. Tipos de fluidização
(A) Fluidização particulada:
Ocorre quando a densidade das
partículas é parecida com a do
fluido e o diâmetro das partículas
é pequeno.
Video sobre fluidização particulada:
http://www.youtube.com/watch?v=waohqAsKCxU&feature=related
29
(B) Fluidização agregativa:
Ocorre quando as densidades das partículas e do fluído são
muito diferentes ou quando o diâmetro das partículas é
grande.
Video sobre fluidização agregativa:
http://www.youtube.com/watch?v=NXJhjhQFBNk&NR=1
http://www.youtube.com/watch?v=8n78CDI3GoU&feature=related
30
5.3. Altura do leito poroso
Quando inicia-se a fluidização, há um aumento da
porosidade e da altura do leito. Essa relação é dada pela
seguinte expressão:
S L1 (1  1 )  S L2 (1   2 )
volume de sólidos
no leito fixo
volume de sólidos
no leito fluidizado
[14]
S
S
L2 (1  1 )

L1 (1   2 )
L2
2
L1
1
31
Sem fluxo
Com fluxo
5.4. Velocidade mínima de fluidização
O leito somente fluidizará a partir de um certo valor de
velocidade do fluido ascendente. Essa velocidade é
definida como a velocidade mínima de fluidização (vmf).
Fp
Quando atinge-se vmf , a força da
pressão (Fp) e a de empuxo (Fe) se
igualam a força do peso das
partículas do leito (Fg).
Fe
Logo,
Fp + Fe = Fg
Fg
http://www.youtube.com/watch?v=nGovDPNvSDI&feature=related
32
Sabe-se que
Fe
Fp
Fp  P. S
Fg  msólidos g   p SL(1   ) g
Fe  m fluido deslocado g   f SL(1   ) g
Fazendo
L
Fp + Fe = Fg tem-se:
P
 (  p   f )(1   ) g
L
[15]
Fg
33
5.4.1. vmf para regime laminar
Para esse regime, a parte final da equação de Ergun
[13] é insignificante em relação à primeira, logo temos:
(1   ) 2  f
(1   )  f 2
P
 150 2 3 2 v0  1,75
v0
3
L
 p  Dp
 p  Dp
Rearranjando com a equação [15] tem-se:
vmf
2
3

(

)
p   f
1
p
mf

g.Dp2
150 (1   mf )
f
[16]
34
5.4.2. vmf para regime turbulento
Para esse regime, a parte inicial da equação de Ergun
[13] é insignificante em relação à segunda, logo temos:
(1   ) 2  f
(1   )  f 2
P
 150 2 3 2 v0  1,75
v0
3
L
 p  Dp
 p  Dp
Rearranjando com a equação [15] tem-se:
vmf
p   f

3
 0,756
g  p ( mf ) Dp
  f

1/ 2
[17]
35
5.5. Porosidade mínima de fluidização
 Para determiná-la, usam-se as seguintes relações:
 mf 
Vvazios mf
Vleito mf

Vleito mf  Vtotal de partículas sólidas
Vleitomf
 Experimentalmente:
 p .
3
mf
1

14
36
Exercícios
de
Fluidização
37
Ex. 1: Um leito fluidizado possui 80 kg de partículas de diâmetro 60 µm
( = 0,8) e densidade 2500 kg/m3. O diâmetro do leito é 40 cm e a altura
mínima de fluidização é 50 cm. O fluido ascendente é ar ( = 0,62 kg/m3),
que flui em regime turbulento no leito. Calcule:
(a) A porosidade mínima de fluidização.
(b) A perda de carga na altura mínima de fluidização.
(c) A velocidade mínima de fluidização
(a) Volume de sólidos = 80kg / 2500 kg/m3 = 0,032 m3. Para uma
porosidade de 0 (1= zero), a altura do leito considerando apenas sólidos
seria de: L1=Volume/Área=0,032m3/0,1256m2=0,2548 m
Usando [14] tem-se:
S L1 (1  1 )  S L2 (1   2 )  0,2548m(1  0)  0,5m(1   2 )
 2  0,49
No início da fluidização, o leito possui 49% de seu volume
ocupado com ar e os 51% restantes com partículas sólidas
Também poderia ser resolvido por:
 mf 
Vvazios mf
Vleito
mf

Vleito mf  Vtotal de partículas sólidas
Vleito mf
38
(b) De [15] tem-se:
P
 (  p   f )(1   mf ) g
Lmf
P  0,50(2550 0,62)(1  0,49)9,8  6246Pa
Na altura mínima de fluidização, a perda de carga no leito poroso será de 6,3kPa
(c) De [13] tem-se:
150 f vmf Lmf 1   2 1,75 f vmf2 Lmf 1   
P 

2
2
3
 p Dp
 mf
 p Dp
 mf3
vmf  _______m / s
Quando o fluido atingir Vmf se iniciará a fluidização do leito.
39
4 Dp v0  f
Re 
6 (1   )  f
f 
f 

Dp 
vmf 
v0  vmf   0,175
Re  ?
Tipo de escoamento
Consistência?
40
Exercício 2: Velocidade mínima de fluidização
Partículas sólidas possuindo diâmetro de 0,12mm, esfericidade de
0,88 e densidade de 1000kg/m3 irão ser fluidizadas com ar a 2 atm
e 25ºC (=1,84.10-5 Pa.s; =2,37kg/m3). A porosidade mínima de
fluidização é 0,42. Com essas informações encontre:
(a) A altura mínima de fluidização considerando a seção transversal
do leito vazio de 0,30m2 e que o leito contém 300kg de sólidos.
(b) Encontre a queda de pressão nas condições de fluidização
mínima.
(c) Encontre a velocidade mínima de fluidização
(a) Volume de sólidos = 300kg / 1000 kg/m3 = 0,3 m3
Para uma porosidade de 0 (1= zero), a altura do leito
considerando apenas sólidos seria de: L1=0,3m3/0,3m2=1m
Usando [14] tem-se:
S L1 (1  1 )  S L2 (1   2 )  L2 
1m(1  0)
 1,72m
(1  0,42)
No início da
fluidização, o leito
terá 1,72m
41
(b)
De [15] tem-se:
P
 (  p   f )(1   mf ) g
Lmf
P  1,72(1000 2,37)(1  0,42)9,8  9753Pa
Na altura mínima de fluidização, a perda de carga no leito será 9,7kPa
(c) De [15](condições de mínima fluidização) em [13] (Ergun) tem-se:
9753Pa 
9753Pa 
150 f vmf Lmf 1   mf
 D
2
p
 mf
2
p

2

3
150(1,84.105 )vmf (1,72) 1  0,422
2
(0,88) (0,00012)
2
3
0,42
1,75 f vmf2 Lmf 1   mf
 p Dp


 mf 3
1,75(2,37)vmf2 (1,72) 1  0,42
0,88(0,00012)
0,423
Resolvendo tem-se: vmf = 0,00504 m/s
Quando o fluido atingir 0,00504 m/s, a fluidização do leito será
iniciada.
42
Exercício 3: Velocidade mínima de fluidização e expansão do
leito
Partículas sólidas possuindo diâmetro de 0,10mm, esfericidade de
0,86 e densidade de 1200kg/m3 irão ser fluidizadas com ar a 2atm
e 25ºC (=1,84.10-5 Pa.s; =2,37kg/m3). A porosidade mínima de
fluidização é 0,43. O diâmetro do leito é de 0,60m e contém 350kg
de sólidos. Com essas informações encontre:
(a) A altura mínima de fluidização.
(b) Encontre a queda de pressão nas condições de fluidização
mínima.
(c) Encontre a velocidade mínima de fluidização.
(d) Utilizando 4 vezes a velocidade mínima, estime a porosidade do
leito.
Itens (a), (b) e (c) são resolvidos da mesma maneira que o exercício
anterior.
Respostas:
(a) 1,81m;
(b) 12120Pa;
43
(c) 0,004374m/s.
(d) De [15] em [13] (Ergun) tem-se:
(  p   f )(1   ) g 
150 f v 1  
 D
2
p
2
p


2
3
150(1,84.105 )(4 * 0,004374) 1  
(1200 2,37)(1   ) g 
(0,86) 2 (0,0001) 2
3


1,75 f v 2 1  
 p Dp
2



3
1,75(2,37)(4 * 0,004374) 2 1  
0,86(0,0001)


3
Resolvendo tem-se:  = 0,605
Quando o fluido atingir quatro vezes a velocidade mínima de
fluidização, a porosidade do leito será de 0,605, ou seja,
60,5% do volume do leito ocupado com fluido e
39,5% do volume do leito ocupado com as partículas sólidas.
44
Exercício 4: Fluidização em um filtro de areia
Para limpar um filtro de areia, ele é fluidizado à condições mínimas
utilizando água a 24ºC. As partículas arredondadas de areia
possuem densidade de 2550 kg/m3 e um tamanho médio de
0,40mm. A areai possui as seguintes propriedades: esfericidade de
0,86 e porosidade mínima de fluidização de 0,42.
(a) O diâmetro do leito é 0,40m e a altura desejada do leito para as
condições mínimas de fluidização é 1,75m. Calcule a
quantidade de sólidos necessários (massa de areia).
(b) Encontre a queda de pressão nessas condições, e a velocidade
mínima de fluidização.
(c) Utilizando 4 vezes a velocidade mínima de fluidização, estime a
porosidade e altura do leito expandido.
(a) 325,08kg
Respostas:
(b) 15418Pa; 0,00096 m/s
(b)  = 0,536; 2,16m
45