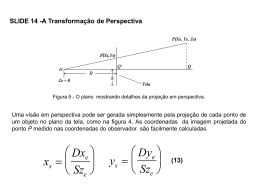
Realidade Virtual
Aula 5
Remis Balaniuk
Objetivo
• Nessa aula vamos aprender como criar
hierarquias de objetos tridimensionais.
Recapitulando
• Como visto na aula passada, as transformações rígidas
dos objetos tridimensionais (translações e rotações) são
controladas por matrizes de transformação homogêneas.
• Tipicamente, numa aplicação em RV, cada objeto tem
associado a ele uma matriz de transformação, que é
inicializada com a matriz identidade.
• É como se essa matriz configurasse um sistema de
coordenadas específico para o objeto.
• Uma transformação rígida ao manipular a matriz de
transformação do objeto manipula na verdade o sistema de
coordenadas do objeto com relação ao mundo, fazendo
com que o objeto mude de posição no mundo sem ter de
mudar de posição dentro do seu sistema de coordenadas.
• Sucessivas transformações rígidas podem ser aplicadas
ao objeto como um todo manipulando só a matriz de
transformação do objeto.
Exemplo
cubo=criaCubo(0.5,world,cVector3d(0,0,0));
braco1->setShowFrame(true);
world->addChild(braco1);
braco1->translate(cVector3d(0.5,0.5,0.5));
braco1->rotate(cVector3d(0.5,0.5,0.5),0.5);
Recapitulando
• Um vértice ao ser criado tem uma posição no espaço
definida.
• Ao ser adicionado a um objeto (mesh), a posição do
vértice passa a ser considerada no sistema de
coordenadas desse objeto, e não mais no do mundo.
• Uma transformação rígida do objeto, ao transformar o
sistema de coordenadas do objeto com relação ao do
mundo, faz com que a posição de todos os vértices do
objeto mudem de posição com relação ao mundo,
mesmo que as posições desses vértices continuem as
mesmas dentro do sistema de coordenadas do objeto.
• Um sequência de transformações concatenadas pode
ser obtida multiplicando sucessivamente a matriz de
transformação do objeto pelas matrizes de cada
transformação .
• O cálculo da posição final de um vértice no mundo é
feita só no momento do render, ou seja, no momento de
apresentar o objeto na tela.
Hierarquias
• Um modelo em RV é tipicamente
construído como uma hierarquia.
Mundo 3D
Objeto 1
Objeto 1.1
Objeto 2
... Objeto 1.n
Objeto 1.n.1 ... Objeto 1.n.m
...
Objeto n
Hierarquias
• Na prática, a hierarquia significa que o sistema de
coordenadas local a um objeto é preso a uma posição e
orientação no sistema de coordenadas do seu pai.
• Uma transformação no sistemas de coordenadas do pai
(sua matriz de transformação) leva junto todos os filhos.
• Uma transformação no filho só afeta o filho e os filhos
desse filho.
• Um objeto pode ser filho do mundo ou de outro objeto.
• Exemplo:
– O objeto1 é filho do mundo
• world->addChild(objeto1);
– O objeto2 é filho do objeto1
• objeto1->addChild(objeto2);
Hierarquias
• Na prática o que acontece é um empilhamento de
matrizes de transformação.
• O algoritmo de render percorre a árvore da hierarquia e
a cada descida para tratar um filho ele acrescenta sua
matriz de transformação à pilha (glPushMatrix()).
• Cada vértice do objeto nm (um neto do mundo) do
exemplo abaixo ao ser apresentado pelo render terá sua
posição calculada como:
– (px’,py’,pz’) = (px,py,pz).M.Mn.Mnm
Matriz do objeto nm (Mnm)
Matriz do objeto n (Mn)
Matriz do mundo (M)
Estratégias de modelagem
• Para fazer uso das hierarquias na
composição de objetos complexos é
preciso levar em consideração a
“semântica” das ligações das partes de
um objeto entre sí.
• A seguir veremos dois exemplos práticos:
Exemplo 1
• Objetos articulados:
– O projeto ‘aula4.bpr’
implementa um braço
articulado com dois
segmentos.
– Cada segmento é um
objeto (cMesh).
– O primeiro segmento é
filho do mundo, o
segundo é filho do
primeiro.
Exemplo 1
// cMesh* criaParalelepipedo(float largura, float altura,
float profundidade, cWorld *world, cVector3d centro);
braco1=criaParalelepipedo(1.0,0.2,0.2,world,cVector3d(0.5,0,0));
braco1->setShowFrame(true);
world->addChild(braco1);
braco2=criaParalelepipedo(0.8,0.1,0.1,world,cVector3d(0.4,0,0));
braco1->addChild(braco2);
braco2->translate(cVector3d(1.0,0,0));
braco2->setShowFrame(true);
• note que são criados dois paralelepípedos, o primeiro mais
grosso ligado à origem do mundo e o segundo mais fino conectado
à extremidade do primeiro.
•duas configurações são importantes nesse exemplo:
• o ponto de pivoteamento da articulação (em torno de que
ponto o segmento gira)
• em que ponto do segmento anterior o segmento seguinte se
liga
Exemplo 1
• ambos os segmentos têm como pivô o centro da face esquerda
• essa definição se faz coincidindo o ponto de pivô com a origem (0,0,0) e
calculando a posição dos demais vértices em função desse ponto.
• a ligação do segundo segmento com o primeiro (articulação) é na extremidade
direita do primeiro segmento.
• essa definição foi feita deslocando o segundo segmento (seu sistema de
coordenadas) de forma a fazer coincidir o ponto de pivô do segundo segmento
com o ponto de articulação no primeiro segmento:
braco2->translate(cVector3d(1.0,0,0));
Exemplo 2
• Sistema planetário:
– o projeto “aula5.bpr” implementa um sistema
composto de 4 esferas que orbitam em diferentes
trajetórias
– o objetivo desse projeto é mostrar como implementar
movimentos compostos baseados em hierarquias.
Exemplo 2
• O problema consiste em definir para cada esfera um
movimento desejado.
• A esfera lilás deve rodar em torno de sí mesma a uma
velocidade de uma volta a cada 2 segundos, e está
posicionada na origem do sistema planetário (sol).
• O planeta verde deve rodar em torno de sí mesmo a uma
velocidade de uma volta a cada 3 segundos e em torno
da origem a uma velocidade de uma volta a cada 4
segundos.
• O planeta azul deve rodar em torno de sí mesmo a uma
velocidade de uma volta a cada 4 segundos e em torno
da origem a uma velocidade de uma volta a cada 6
segundos.
• As rotações do sol e dos planetas são em torno do eixo Y.
• A esfera azul tem uma lua estacionária que gira somente
em torno de sí mesma ao redor do eixo X a uma
velocidade de 1 volta a cada 2 segundos.
Exemplo 2
• A solução do problema exige uma organização de
sistemas de coordenadas para permitir compor todos os
movimentos desejados.
• O movimento do “sol” é uma simples rotação em torno
do eixo Y.
• Como os planetas não rodam na mesma velocidade do
sol, e tem cada um uma velocidade diferente de rotação
em torno do centro, não é possível colocá-los como
filhos do sol.
• Eles também não podem ser filhos do mundo pois o
método cShapeSphere define uma esfera centrada na
origem do sistema de coordenadas. Sendo filhos do
mundo eles poderiam só rodar em torno de sí mesmos.
Exemplo 2
• A solução proposta foi criar um sistema de
coordenadas intermediário para cada planeta
por meio de um cGenericObject vazio.
• Esses sistemas são filhos do mundo, sendo os
planetas filhos desses sistemas.
• Para fazer o planeta girar em torno do sol basta
posiciona-lo na sua órbita e então rotacionar o
sistema ao qual esse está ligado.
• A rotação do planeta em torno de sí mesmo é
obtido através de um rotate básico.
Exemplo 2
• A lua do planeta azul foi colocada como
sua filha pois sendo essa estacionária vai
girar junto com a rotação do planeta azul
em torno de sí mesmo.
• (observação: as explicações sobre as
classes cMaterial e cShapeSphere serão
feitas em outra aula).
Câmeras
• Note que a implementação das câmeras
também se faz através de transformações,
chamadas de “transformações de
visualização”
• Os comandos de posicionamento da
câmera são usados para definir a matriz
de transformação de visualização dessa
câmera.
Câmeras
• Na prática é como se na base da pilha de
matrizes de transformação estivesse a
matriz relativa à transformação de
visualização, que define onde cada vértice
do mundo aparece na tela.
Matriz do objeto nm (Mnm)
Matriz do objeto n (Mn)
Matriz do mundo (M)
Matriz da câmera
Exercícios
1) Altere o projeto “aula4.bpr” de forma a
estender o braço ajuntando uma pinça
que pode girar (como um pulso) e abrir e
fechar.
Exercícios
2) Estender o projeto “aula5.bpr” de forma
que a lua do planeta azul possa também
rodar em torno do planeta ao redor do
eixo z a uma velocidade de uma volta a
cada 5 segundos.
Exercícios
3) Implemente o objeto abaixo. Ele é composto
por uma base quadrada giratória, dois pilares
presos à base, uma viga presa aos pilares, uma
haste presa a viga e uma esfera presa à haste.
O conjunto viga, haste e esfera gira em torno do
eixo da viga.