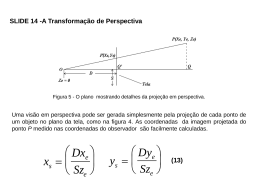
SLIDE 14 -A Transformação de Perspectiva
Figura 5 - O plano mostrando detalhes da projeção em perspectiva.
Uma visão em perspectiva pode ser gerada simplesmente pela projeção de cada ponto de
um objeto no plano da tela, como na figura 4. As coordenadas da imagem projetada do
ponto P medido nas coordenadas do observador são facilmente calculadas.
 Dxe 

xs  
 Sze 
 Dye 

ys  
 Sze 
(13)
SLIDE 15 -A Transformação de Perspectiva
Alternativamente, podemos converter para coordenadas de tela, incluindo uma especificação
da localização da janela pela qual a imagem é mostrada
 Dxe 
 Vsx  Vcx
xs  
 Sze 
 Dye 
 Vsy  Vcy
ys  
 Sze 
(14)
Os quatro parâmetros são dados em notação “center-size”: a janela está centrada em , tem
unidades de altura e unidades de largura. Estes quatro parâmetros podem ser determinados
a partir dos parâmetros da janela de visualização.
A transformação de perspectiva é fundamentalmente diferente daquela para rotação,
translação e mudança de escala: ela envolve divisão pelo valor da coordenada , enquanto as
outras envolvem apenas multiplicações e adições. Gerar uma imagem em perspectiva
verdadeira, requer divisão pela profundidade de cada ponto.
S
Imagem
Vista 2
Vista 1
D1
D2
. Se a razão D/S for pequena, abertura será “ampla” e produzirá imagens
similares àquelas de ângulo aberto.
. Uma razão D/S grande especifica uma abertura “estreita”
correspondendo a vistas do tipo “telefoto”
Uma razão D/S grande especifica uma
abertura “estreita” correspondendo a
vistas do tipo “telefoto” como a foto
acima
Se a razão D/S for pequena, abertura será
“ampla” e produzirá imagens similares
àquelas de ângulo aberto como a foto
acima
SLIDE 16 – Clipping tridimensional
É possível demonstrar que:
D
 ze    xe   ze
S
D
 ze    ye   ze
S
(14)
SLIDE 17 – Clipping tridimensional
Por conveniência da tarefa de recorte, definiremos um novo sistema de
coordenadas, “o sistema de coordenadas de clipping”, em função do sistema
de coordenadas do observador
xc
yc
zc 1  xe
Onde
ye
ze 1N
D / S
 0
N 
 0

 0
c
 zc  xc   zc
e
 zc  yc   zc
0
0 0
D / S 0 0
0
1 0

0
0 1
(14)
SLIDE 17 – Clipping tridimensional
Reescrevedo a equação 14
 xc 
xs   Vsx  Vcx
 zc 
(14)
c
 yc 
y s   Vsx  Vcx
 zc 
SLIDE 18 - Visão em perspectiva de um cubo
Considere um cubo centrado na origem do sistema de coordenadas do “mundo”, definido
pelos seguintes pontos e linhas
Linhas
Pontos
x
y
z
AB, BC,
A
-1
1
-1
CD, DA,
B
1
1
-1
EF, FG,
C
1
-1
-1
GH, HE
D
-1
-1
-1
AE, BF,
E
-1
1
1
CG, DH
F
1
1
1
G
1
-1
1
H
-1
-1
1
Vamos observar este cubo a partir do ponto (6,8,7.5), com o eixo de visualização apontando
diretamente para a origem do sistema de coordenadas do “mundo”. Existe ainda um grau de
liberdade sobrando, que é uma rotação arbitrária em torno do eixo : vamos assumir que o eixo
está no plano z = 7.5.
SLIDE 19 - Visão em perspectiva de um cubo
Figura 10 - Cinco passos para realizar a transformação de visualização: (a) Translação; (b) Rotação em
torno do eixo x; (c) Rotação em torno do eixo y; (d) Rotação em torno do eixo x; (e) Invertendo o eixo z.
1) O sistema de coordenadas é transladado para (6,8,7.5), como mostrado
na figura (a). O ponto (6,8,7.5) no sistema de coordenadas original
passa a ser a origem:
x
y z  1  x
Operação desejada
y
1
0
z 1
0

Tx
0
0
1
0
0
1
Ty
Tz
Matriz Translação
Resultando
Note que usamos a operação inversa (-6, -8, -7.5)
0
0
 1
 0
1
0

T1 
 0
0
1

 6  8  7.5
0
0

0

1
0
0
0

1
2) Rotação de -90 do sistema de coordenadas em torno do eixo “x’”, como
mostrada na figura (b). Observe que, devido à utilização da transformação
inversa, substituímos  = 90 na equação de rotação em torno do eixo “x”.
 x
y z 1   x
0
 sin
cos 
0
Matriz de Rotação de um ângulo ,
em torno de do eixo X
Operação desejada
Resultando
0
1
0 cos 
y z 1
0 sin
0
0
1
0
T2  
0

0
0 0
0 1
1 0
0 0
0
0

0

1
0
0

0
1
3) Rotação em torno do eixo y’ , de um ângulo , tal que o eixo z’ fique na
direção do eixo z (embora no sentido contrário), como mostrado na figura (c).
Novamente devemos utilizar a transformação inversa.
x
y
0 sin
1
0
0 cos
0
0
Matriz de Rotação de um ângulo ,
em torno de do eixo Y
Operação desejada
Resultando
y z 1  x
 cos
 0
z 1
 sin

 0
 0.8
 0
T3  
 0.6

 0
0 0.6
1
0
0  0.8
0
0
0
0
0

1
0
0
0

1
4) Rotação em torno do eixo X’ , de um ângulo , tal que a origem do sistema de
coordenadas original fique sobre o eixo , como mostrado na figura (d).
Novamente devemos utilizar a transformação inversa.
 x
Operação desejada
y z 1   x
0
1
0 cos 
y z 1
0 sin
0
0
0
 sin
cos 
0
0
0

0
1
Matriz de Rotação de um ângulo ,
em torno de do eixo X
0
0 0
1
Resultando
0 0.8 0.6 0

T4  
0  0.6 0.8 0


0
0 1
0
5) Finalmente, invertendo o sentido do eixo z , de modo a criar um sistema de
coordenadas de “mão-esquerda”, de acordo com as convenções do sistema de
coordenadas do observador, como mostrado na figura (e). Uma matriz de
mudança de escala é utilizada. Esta operação completa as cinco
transformações primitivas necessárias para estabelecer a transformação de
visualização.
 x
Operação desejada
Resultando
y z 1   x
 Sx
0
y z 1
0
 0
0
Sy
0
0
0
0
Sz
0
Matriz de Mudança de escala
1
0
T5  
0

0
0 0
1 0
0 1
0 0
0
0
0

1
0
0

0
1
Suponha que desejamos preencher uma tela de 30 cm x
30 cm, desenhada para ser vista de uma distância de
60 cm, e cujo o sistema de coordenadas da tela vai de 0
a 1023. Assim, D = 60, S = 15, e a transformação
resultante será
SLIDE 21 - Visão em perspectiva de um cubo
4
0
N 
0

0
0
4
0
0
0
0
1
0
0
0

0

1
e a equação 18 passa a ser
x 
xs  5115
.  c z   5115
.
c
y 
ys  5115
.  c z   5115
.
c
(23)
Todos os detalhes das transformações já foram especificados. Cada vértice do cubo é
transformado pela matriz VN, sofre um processo de “clipping”, e convertido para
coordenadas de tela usando-se a equação 23.
 3.2  1.44  0.48
 2.4  1.92  0.64
V  T1T2 T3T4 T5 N  
 0
3.2
 0.6

0
12.5
 0
0
0

0

1
SLIDE 22 - Visão em perspectiva de um cubo
Podemos agora aplicar esta transformação aos oito vértices do cubo:
xc
yc
zc
A
5.6
-3.68
12.94
B
-0.8
-6.56
11.98
C
-5.6
-2.72
13.26
D
0.8
0.16
14.22
E
5.6
2.72
11.74
F
-0.8
-0.16
10.78
G
-5.6
3.68
12.06
H
0.8
6.56
13.02
SLIDE 23 - Visão em perspectiva de um cubo
Apesar da necessidade da rotina de “clipping” ser aplicada a cada linha no cubo, está
aparente na tabela que todos os vértices estão dentro da pirâmide de visualização, e o
algoritmo de “clipping” irá aceitar trivialmente todas as linhas. As coordenadas de tela das
extremidades das linhas são calculadas com a equação 23, e as linhas são desenhadas
como mostrado na figura 11.
Figura 11 - A visão em perspectiva do cubo, gerada pelos cálculos do exemplo do texto.