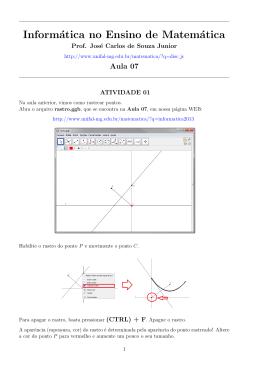
Tecnologias no Ensino de Matemática
Profa. Andréa Cardoso
ROTEIRO DA ATIVIDADE PRÁTICA 2
Data da realização: 10 de março de 2015
Objetivo da atividade: Explorar funcionalidades do GeoGebra.
ATIVIDADE 01: CONSTRUÇÃO DE UM TRIÂNGULO EQUILÁTERO
Nesta atividade, usaremos os recursos aprendidos para criar um triângulo equilátero.
Passo 01: Abra um novo arquivo com a disposição Geometria.
Passo 02: Use a ferramenta que constrói segmentos para desenhar a base do triângulo equilátero.
Passo 03: Use agora a ferramenta que constrói cı́rculos. Desenhe um cı́rculo de centro no ponto
A, passando pelo ponto B.
Passo 04: Em seguida, construa um cı́rculo de centro no ponto B e que passa pelo ponto A.
1
Passo 05: Para marcar um ponto de interseção dos dois cı́rculos, que será o terceiro vértice
do triângulo equilátero, basta selecionar a opção Interseção de Dois Objetos, na segunda
janela da Barra de Ferramentas. Em seguida, clique nas duas circunferências.
Passo 06: Com o terceiro vértice construı́do, podemos desenhar os dois lados do triângulo que
faltam! Selecione a ferramenta Segmento definido por Dois Pontos e crie os segmentos
AC e BC.
Passo 07: Um recurso muito útil é o de esconder construções auxiliares, como é o caso dos dois
cı́rculos. Isso ajuda a manter a construção “limpa”.
Para esconder um objeto, primeiro posicione o apontador do mouse sobre ele. Depois, clique
com o botão direito do mouse e desmarque a opção Exibir Objeto.
2
Após esconder os cı́rculos e o ponto D, ficamos com a seguinte figura:
É importante ter em mente que os dois cı́rculos não foram apagados! Eles estão apenas escondidos!
Passo 08: Mova os pontos livres, os objetos dependentes se moverão de acordo, mas sempre
produzindo um triângulo equilátero!
Passo 09: Caso você queira exibir os objetos que foram escondidos, ative a ferramenta Exibir/Esconder Objeto e então, clique nos objetos que você quer recolocar na construção!
Depois selecione a opção Mover. Pronto! Irão aparecer as construções desejadas!
ATIVIDADE 02: RETAS PERPENDICULARES
Abra um arquivo novo e escolha a disposição Geometria. Vamos aprender a usar a ferramenta
que traça retas perpendiculares.
Usaremos essa ferramenta para construir um quadrado dado um de seus lados.
Passo 01: Vamos começar desenhando um lado do quadrado. Selecione a ferramenta Segmento
definido por Dois Pontos e crie um segmento de reta.
Passo 02: Vamos ativar a ferramenta que traça retas perpendiculares a retas, semirretas e
segmentos.
3
Para construir a perpendicular, você deve especificar primeiro, o segmento ao qual a reta será
perpendicular e depois, um ponto por onde ela passará.
Passo 03: Usaremos agora a ferramenta que constrói cı́rculos.
4
Crie dois cı́rculos. O primeiro, com centro em A e passando pelo ponto B. E o segundo, com
centro em B e passando por A.
Passo 04: Usaremos agora a ferramenta que constrói pontos para marcar as interseções dos
cı́rculos com as retas perpendiculares.
Passo 05: Agora que acabamos de construir os outros vértices do quadrado, vamos esconder
as construções auxiliares, usando a ferramenta Exibir/Esconder Objeto. Oculte as duas
circunferências, as retas perpendiculares e os pontos C e E.
Passo 06: Pronto. Só resta agora desenhar os lados que faltam! Trace os segmentos AD, DF e
BF .
5
Passo 07: Mova os pontos livres! Os outros vértices e segmentos se moverão também, mas
sempre formando um quadrado!
ATIVIDADE 02: SELEÇÃO MÚLTIPLA.
Exiba todas as construções auxiliares realizadas na parte 11.
Agora veremos um outro modo de esconder vários objetos! Em nosso exemplo, esconderemos
as duas retas, os dois cı́rculos e os pontos C e E da construção!
Passo 01: Selecione a opção Mover na primeira janela da barra de ferramentas e, então, com
um clique do botão esquerdo do mouse, selecione o primeiro objeto.
Passo 02: Agora, com a tecla CTRL pressionada, selecione os outros objetos com cliques do
botão esquerdo do mouse. Note que os objetos selecionados mudam de aparência, conforme a
figura anterior.
6
Passo 03: Agora é só clicar com o botão direito do mouse sobre um dos objetos selecionados e,
então, desmarcar a opção “Exibir Objeto”.
Obtendo assim,
ATIVIDADE 03: RETAS PARALELAS
Abra um arquivo novo e escolha a disposição Geometria. Vamos aprender a usar a ferramenta
que traça retas paralelas.
Usaremos essa ferramenta para construir um paralelogramo, dado dois de seus lados.
Passo 01: Use a ferramenta Segmento definido por Dois Pontos, localizado na terceira
janela da barra de ferramentas, para desenhar dois lados adjacentes do paralelogramo.
7
Passo 02: Selecione a ferramenta Reta Paralela e trace as retas paralelas ao segmentos,
passando pelos pontos B e C. Para construir uma reta paralela, você deve especificar primeiro
o segmento ao qual a reta será paralela e, depois, um ponto por onde ela passará.
Passo 03: Use a ferramenta Interseção de Dois Objetos para marcar a interseção das duas
retas construı́das.
Passo 04: Use a ferramenta Exibir/Esconder Objeto para ocultar as construções auxiliares.
Esconda as retas paralelas!
8
Passo 05: Use a ferramenta Segmento definido por Dois Pontos para desenhar os lados
que faltam.
Passo 06: Vamos agora, usar uma ferramenta decorativa que permite desenhar polı́gonos coloridos. Primeiro, selecione a ferramenta Polı́gono. Depois, selecione os vértices do polı́gono,
sendo que o último vértice selecionado deve coincidir com o primeiro!
Se você mover os pontos livres, os outros vértices e segmentos se moverão também, mas sempre
formando um paralelogramo!
ATIVIDADE 04: CONSTRUÇÃO DE UM HEXÁGONO REGULAR.
Você já viu como construir um triângulo equilátero e um quadrado no GeoGebra. Neste
exercı́cio você é convidado a construir um hexágono regular, dado um de seus lados! Seu
desenho final deve exibir apenas os 6 lados e os 6 vértices do hexágono regular (esconda todas as construções auxiliares). Mais ainda, os 6 vértices devem estar rotulados pelas letras
A, B, C, D, E e F , em sequência.
Nesta atividade não é permitido o uso da ferramenta Polı́gono Regular!
Dica: Observe a seguinte propriedade do hexágono regular:
9
ATIVIDADE 05.
Desenhe um quadrilátero ABCD e, em seguida, marque os pontos médios X, Y, W e Z do
segmentos AB, BC, CD e DA, respectivamente. Não é necessário renomear os pontos em sua
construção (você aprenderá como renomear objetos em uma próxima aula).
(a) Implemente esta construção no GeoGebra. Quais são os pontos livres?
(b) Que propriedade marcante o quadrilátero XY W Z possui? Faça uma conjectura e prove-a!
ATIVIDADE 06.
Dados dois pontos livres A e B, construa um retângulo cuja base é o segmento AB e cuja altura
tenha medida igual a metade da medida da base. O retângulo deve estar preenchido com a cor
amarela, com transparência de 50%. Os vértices e as arestas do retângulo devem estar todos
na cor azul. Os vértices devem estar rotulados com os nomes A, B, C e D. Sua construção
deve manter todas essas propriedades indicadas mesmo quando os pontos livres são movidos de
lugar.
ATIVIDADE 07.
Construa um quadrado ABCD em seguida construa também um um quadrilátero EFGH
inscrito no quadrado.
10
(a) Em que condições o quadrilátero é um retângulo?
(b) De quantas formas distintas você consegue verificar a existência de um retângulo?
Dica: Para fazer com que o quadrilátero inscrito seja um retângulo, construa o quadrilátero
inscrito fixando retos três de seus ângulos.
ATIVIDADE 08.
Agora que você conhece um pouco mais sobre o funcionamento do GeoGebra, leia estes dois
artigos que discutem o potencial didático dos softwares de geometria dinâmica:
1. George de Souza Alvez e Adriana Benevides Soares. “Geometria Dinâmica : um estudo de
seus recursos, potencialidades e limitações através do software Tabulae”, XXIII Congresso
da Sociedade Brasileira de Computação, Campinas, 2003.
2. Maria Alice Gravina. “Geometria Dinâmica: Uma Nova Abordagem para o Aprendizado
da Geometria”, Anais do VII Simpósio Brasileiro de Informática na Educação, pp. 1-13,
Belo Horizonte, 1996.
Estes artigos estão disponı́veis no link “Biblioteca” na página WEB:
http://www.unifal-mg.edu.br/matematica/?q=informatica2013
Faça uma análise destes textos, procurando contrapor as ideias expostas com a sua experiência
pessoal com um software de geometria dinâmica, no caso, o GeoGebra. Procure explicar, com
suas próprias palavras, o significado de “invariante geométrico”.
Envie a sua resposta por e-mail, com assunto “Atividade Prática 2”anexe seu arquivo nomeado
de acordo com o modelo “AT 2 nome”.
11