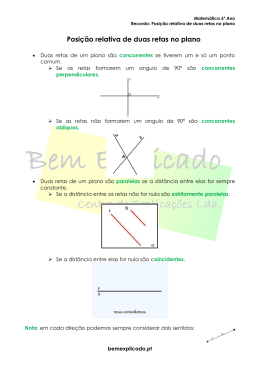
Resumo de Geometria Analítica (terceirão)
1. Distância entre os pontos A( x A , y A ) e B( xB , y B )  d 
xB  x A 2  ( y B  y A ) 2 .
2. Distância entre o ponto P( x0 , y0 ) e a reta r : ax  by  c  0  d 
ax0  by0  c
a2  b2
.
 x  xB y A  y B 
3. Ponto médio de A( x A , y A ) e B( xB , y B )  M  A
,
.
2
 2

4. Equação da reta que passa por A( x A , y A ) e B( xB , y B ) :

xA
Forma geral: x B
x
yA 1
y B 1  0  ax  by  c  0 .
y 1
yB  y A
.
xB  x A

Forma reduzida: y  mx  n , onde m  tg ou m 

“Iô-iô mi xô-xô”  y  y0  m( x  x0 ) .

Forma segmentária:

Forma paramétrica: x e y são dados em função de um parâmetro.
x y
  1 , quando a reta passa por P( p,0) e Q(0, q) .
p q
5. Posições relativas das retas r : y  mr x  nr e s : y  ms x  ns :

nr  ns  retas paralelas coincidentes.
mr  m s  
nr  ns  retas paralelas distintas.

mr  ms  1  retas concorrentes.
mr  m s  
mr  ms  1  retas perpendiculares.
xA
1
6. Área do triângulo de vértices A( x A , y A ) , B( xB , y B ) e C ( xC , yC ) : A  x B
2
xC
7. Equação da circunferência de centro C (a, b) e raio R: ( x  a) 2  ( y  b) 2  R 2 .
yA 1
yB 1 .
yC 1