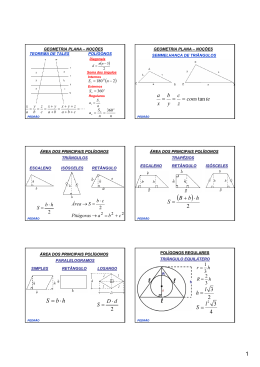
MATRIZES
L i Co
( )mxn
A = aij
PEDRÃO
PEDRÃO
− Bt
+ B) ⋅ B t
c) ( A
d) B
e)
t
⋅A
A ⋅B
PEDRÃO
a) 5
b) 6
c) –6
d) 4
e) 0
PRODUTO DE MATRIZES
Li
Am x p
Co
x
Bp x n
=
Cmxn
PEDRÃO
Se A e B são matrizes do tipo 2x3, qual das
seguintes operações não pode ser efetuada?
a) A + B
t
⎧i − j, se i = j
aij = ⎨
⎩2i + j, se i ≠ j
PEDRÃO
Dadas At = [10 6 5], Bt = [8 2 2] e Ct = [−6 0 −4],
tal que 2A − B + 2M + C = 0, a matriz Mt é igual a:
a) [– 3 5 2]
b) [– 3 – 5 – 2]
c) [– 3 – 5 2]
d) [ 3 – 5 – 2]
e) [ 3 5 – 2]
b) A
Sendo A uma matriz de ordem 3x3, cujos
elementos são dados pela função abaixo, a soma
dos elementos da diagonal principal é:
Considere as matrizes de elementos reais abaixo.
Sabendo-se que A . B = C , pode-se afirmar que o
produto dos elementos de A é:
⎡1 x⎤
A=⎢
⎥
⎣y z⎦
⎡1 1⎤
B=⎢
⎥
⎣1 2⎦
⎡3 5 ⎤
C=⎢
⎥
⎣9 14⎦
a) 20
b) 30
c) 40
d) 50
PEDRÃO
1
MATRIZ INVERSA
A ⋅ A −1 = A −1 ⋅ A = In
Dada a matriz
A−1.
⎡ 1 2⎤
A=⎢
⎥ , encontre sua inversa
⎣3 4⎦
PEDRÃO
⎣y⎦
PEDRÃO
⎡1000 ⎤
a) 10 4 ⎢
⎥
⎣1600 ⎦
Um construtor tem contratos para construir 2 estilos
de casa: moderno e colonial. A quantidade de
material empregado em cada tipo de casa é dada
pela matriz abaixo. Suponha que o construtor vá
construir 2 casas do tipo moderno e 3 do tipo
colonial. Se os preços por unidade de ferro, madeira
e tijolo são, respectivamente, R$15,00, R$8,00 e
R$10,00, então o custo total do material empregado
é igual a
a) R$1923,00.
b) R$1602,00.
c) R$1973,00.
d) R$1932,00.
⎡1020 ⎤
b) 10 6 ⎢
⎥
⎣1680 ⎦
⎡1200 ⎤
c) 10 4 ⎢
⎥
⎣1800 ⎦
⎡ 980 ⎤
d) 10 6 ⎢
⎥
⎣1400 ⎦
⎡1000 ⎤
e) 10 6 ⎢
⎥
⎣1580 ⎦
PEDRÃO
PEDRÃO
Linha e Coluna
Matriz, do LiCo, eu vou lembrar,
Na oposta o sinal vai trocar,
A tabela 1 mostra as quantidades de grãos dos
tipos G1 e G2 produzidos, em milhões de
toneladas por ano, pelas regiões agrícolas A e B.
A tabela 2 indica o preço de venda desses grãos.
Sendo x o total arrecadado com a venda dos
grãos produzidos pela
⎡x⎤
região A e y pela região B, a matriz ⎢ ⎥ é
DETERMINANTES
–A
E linha por coluna, se for transpor.
2ª ORDEM (Regra de Sarrus)
Sarrus)
At
Matriz, na identidade, a diagonal principal,
Meu caro, é tudo um, é igual,
Mas fora dela, zeros vou pôr.
⎡1 0 0⎤
I = ⎢⎢0 1 0⎥⎥
⎢⎣0 0 1⎥⎦
Saiba que com a mesma ordem, eu posso
igualar,
1 2
⎛1 2 ⎞
⎟⎟ → det(A) =
matriz A = ⎜⎜
3 4
⎝3 4⎠
d.s.
d.s.
Diminuir, e até somar,
d.p.
d.p.
Deixou de lado a divisão.
det(A) = 1.4 – 2.3 = 4 – 6 = – 2
E pra uma por outra multiplicar,
Quero na ordem de todas o “meio” igualar,
A mxp x Bpxn = Cmxn
Se pegar os “de fora”, me dão a solução.
Matriz, eu sei que a inversa enche o saco,
A ⋅ A −1 = A −1 ⋅ A = In
Mas todo produto fica chato,
Com sistema muito pior então.
PEDRÃO
PEDRÃO
2
Marcando-se, sobre uma reta real, os pontos
correspondentes às raízes da equação abaixo,
obtém-se um segmento cujo comprimento mede:
a) 1
x x
b) 2
=3
c) 3
2 x
d) 4
PEDRÃO
Dadas as matrizes abaixo, o produto das raízes da
equação det(A+B) = 0 é:
a) 1
⎛a − a⎞
⎛ 3a 2 ⎞
b) 2
⎟⎟
A = ⎜⎜
⎟⎟
B = ⎜⎜
c) – 1/2
1
a
1
1
⎠
⎝
⎝
⎠
d) 3/2
e) – 1
PEDRÃO
DETERMINANTES
MATRIZ INVERSA (regra prá
prática)
3ª ORDEM
⎡1
A=⎢
⎣1
2⎤
1
→ det( A) =
3⎥⎦
1
2
3
1
4
det( A) = 3 − 2 = 1
⎡1
A=⎢
⎣1
ss
⎡ 3
⎢ det( A)
A =⎢
⎢ −1
⎢ det( A)
⎣
−1
2⎤
3⎥⎦
→
⎡3
⎢− 1
⎣
− 2⎤
1 ⎥⎦
2 −3 −2
pp
−2 ⎤
det( A) ⎥
⎥ →
1 ⎥
det( A) ⎥⎦
−1 0
3 −4
⎡ 3 − 2⎤
A−1 = ⎢
⎥
⎣− 1 1 ⎦
PEDRÃO
O determinante a seguir é igual a:
PEDRÃO
1 −1
1
3
2
2
0
2
1
1
1
Resolvendo a equação 1
x
1
−2
x
1
3 = 0 , obtemos:
2
9
a) –21
b) –3
c) 1
d) 5
e) 21
PEDRÃO
PEDRÃO
3
DETERMINANTES – Principais propriedades
DETERMINANTES – Principais propriedades
Quando todos os elementos de uma fila forem
nulos, o determinante vale zero
det(At) = det(A)
Quando os elementos de uma fila forem iguais
ou proporcionais aos de outra fila paralela, o
determinante vale zero
Quando multiplicamos os elementos de uma fila
por um número, o valor do determinante ficará
multiplicado por este número.
PEDRÃO
PEDRÃO
DETERMINANTES – Principais propriedades
A tem ordem n, então det(k.A) =
kn.det(A)
Dadas as matrizes abaixo, a soma das raízes da
equação det(A x B) = – 28 é:
⎛1 x⎞
⎟⎟
A = ⎜⎜
⎝ 5 1⎠
⎛ 2 1⎞
⎟⎟
B = ⎜⎜
⎝4 x⎠
det(A.B) = det(A).det(B)
det(A-1) =
1
det( A )
PEDRÃO
PEDRÃO
Considere as matrizes reais 3×3 abaixo, em que c
é um número real. Sabendo-se que o valor do
determinante da matriz produto A⋅B é −60, calcular
o valor de c.
⎛ 1 2 3⎞
⎜
⎟
A = ⎜0 − 1 2⎟
⎜0 0 3⎟
⎝
⎠
PEDRÃO
⎛c 1 0⎞
⎜
⎟
B = ⎜0 2 0⎟
⎜ 0 0 1⎟
⎝
⎠
PEDRÃO
4