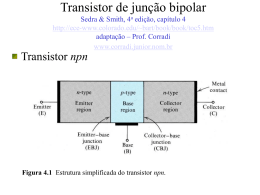
O inversor lógico básico empregando TJB
Livro texto, item 4.14 (4a edição)
Vimos como vantagens do uso do TJB
para implementação do inversor:
A dissipação de potência no circuito é
relativamente baixa, tanto no corte quanto
na saturação: no corte todas as correntes
são zero (exceto pelas pequenas correntes
de fuga); em saturação a tensão sobre o
transistor é muito pequena (VCEsat).
Os níveis de tensão de saída (VCC e VCEsat)
são bem definidos. Em contraposição, se o
transistor opera na região ativa, vO = VCC –
RC iC = VCC – b iB RC , que é fortemente
dependente do parâmetro b do transistor,
que por sua vez é pouco controlável.
A característica de transferência de tensão
Característica de transferência 
Aproximada por 3 segmentos de reta
(retas assintóticas) correspondentes à
operação do TJB nas regiões de corte,
ativa e saturação, conforme indicado.
Determinar as coordenadas
dos pontos notáveis da
característica de transferência,
para: RB = 10 kW, RC = 1 kW,
b = 50 e VCC = 5 V.
A característica de transferência de tensão (2)
 vI  VOL  VCEsat  0,2 V  vO  VOH  VCC  5 V.
 vI  VIL : o transistor inicia a condução  VIL  0,7 V
 VIL  vI  VIH : o transisto r está na região ativa : amplificad or.
RC
vo
 Ganho para pequenos sinais : A v    b
vi
RB  r
Ganho A v  depende do valor de r  determinado por IC e,  ,
pelo valor de vI .
RC
1
Se  IC   r  RB >> r  A v   b
 50   5 V/V
RB
10
 vI  VIH : o transistor inicia a saturação  VIH é o valor de vI para :
I B  I B ( EOS ) 
(VCC  VCEsat ) / RC
b
A característica de transferência de tensão (3)
Para os valores aqui utilizados:
I B (EOS)  0,096 mA  VIH  I B (EOS) RB  VBE  1,66 V
 vI  VOH  5 V : o transisto r está fortemente saturado :
vO  VCEsat  0,2 V e b
forçado

VCC  VCE  RC
sat
VOH  VBE  RB
4,8

 1,1
0,43
As margens de ruído podem agora ser determinadas por (reveja a
seção 1.7 do livro texto):
MRH  VOH  VIH  5  1,66  3,34 V
MRL  VIL  VOL  0,7  0,2  0,5 V
As duas margens de ruído são muito diferentes  este circuito é
pouco ideal (por que?).
A característica de transferência de tensão (4)
O ganho na região de transição pode ser determinado a partir das
coordenadas dos pontos notáveis X e Y:
Ganho de tensão  
5  0,2
 5 V/V
1,66  0,7
Observe que o fato de ser exatamente o mesmo valor encontrado
anteriormente é uma coincidência.
Circuitos TTL: transistor – transistor logic.  Circuitos lógicos com
TJB saturado.
Limitação de velocidade de operação em razão dos tempos de atraso
relativamente longos necessários para cortar um transistor saturado.
Para atingir velocidades de resposta elevadas, o TJB não deve entrar na
saturação.
Armazenamento de cargas portadoras minoritárias na base de um
transistor saturado.  Leiam com cuidado este item do livro texto, para
melhor entender a limitação de velocidade de operação.
Características estáticas completas
Livro texto, item 4.15 (4a edição)
Capacitâncias internas e efeitos de segunda ordem.
iC – vCB: Características de base comum - (npn).
vCB < 0 : JCB  diretamente polarizada  iC diminui, iE const.
 iB aumenta em um valor igual à diminuição em iC (saturação).
Características de base comum
Observe que, na região ativa, as curvas características
apresentam uma pequena inclinação  Indica que, na
configuração BC, iC depende um pouco da tensão vCB (uma
manifestação do efeito Early).
No entanto, a inclinação das curvas iC – vCB medidas para uma
corrente iE constante é muito menor que a inclinação das curvas
iC – vCE medidas para uma tensão vBE constante.  Isto é, a
resistência de saída da configuração BC é muito maior do que a
do circuito EC com vBE constante (i.e, ro).
Outro ponto importante: uma vez que iC – vCB é medida para iE
constante, um aumento de iC com vCB implica uma
correspondnete redução em iB.  A dependência de iB com vCB:
adição de um resistor rm entre C e B no modelo -híbrido 
modelo expandido.
Características de base comum (2)
rm
Figura 4.64 O modelo -híbrido,
incluindo a resistência rm , que
modela o efeito de vc em ib .
 rm é tipicamente maior que b ro .
Este modelo -híbrido expandido pode ser usado para
determinar a resistência de saída Rsaída da configuração BC = o
inverso da inclinação das linhas das curvas características iC –
vCB
B aterrada; E em aberto (iE é constante); aplique uma tensão
entre C e o terra e determine a corrente drenada da tensão de
teste.  Rsaída  rm // b ro (muito elevada)
Características de emissor comum
Figura 4.65
Características
de
emissor comum. Note
que a escala horizontal
foi expandida em torno
da origem para mostrar
a região de saturação
em mais detalhe.
iB é mantida constante para cada curva iC  vCE (diferentemente
da figura 4.15, em que vBE era mantida constante).  A
inclinação na região ativa é diferente de 1 / ro . No caso, a
inclinação é maior.
Características de emissor comum (2)
Pode-se mostrar (vide problema 4.47) que a resistência de saída da
configuração EC para iB constante é aproximadamente igual a [ro //
(rm/b].
Na região ativa: o transistor atua como uma fonte de corrente com uma
resistência de saída elevada (mas finita).
Na região de saturação: o transistor se comporta como uma “chave
fechada” com uma pequena “resistência de fechamento” RCEsat.
Na saturação, as curvas não se diritem para a origem.  Para um dado
valor de iB, a característica iC  vCE na saturação pode ser aproximada
por uma linha reta que intercepta o eixo vCE em um ponto VCEoff – tensão
residual (offset) da chave transistorizada. Transistores de efeito de
campo (FET) não apresentam tais tensões residuais e, portanto, se
apresentam como chaves mais ideais.
FETs, no entanto, apresentam valores maiores de resistência de
fechamento.
Características de emissor comum (3)
Figura 4.66 Uma visão expandida das
características de EC na região de
saturação.
Figura 4.67 Uma das curvas características
iC – vCE na região de saturação. Note que a
característica pode ser modelada por uma
tensão residual VCEoff e por uma resistência
de pequeno valor RCEsat.
O comportamento do TJB na saturação – figura 4.67 – segue de
perto o previsto pela equação 4.114 (VCEsat), obtida a partir do
modelo de Ebers-Moll.
O b do transistor
Transistor: operando com uma corrente de base IBQ, uma corrente
de coletor ICQ e uma tensão C–E VCEQ .  Definido o ponto de
operação Q.
 A razão entre ICQ e IBQ é chamada de b cc ou hFE (parâmetro h
direto na configuração emissor comum – vide Apêndice B –
Parâmetros de quadripolos).
I CQ
hFE  b cc 
I BQ
Transistor – usado como um amplificador  é primeiramente
polarizado em um ponto Q.  Sinais aplicados ao circuito causam
mudanças incrementais em iB, iC e vCE em torno de Q.
 Pode-se definir um b incremental ou ca mantendo a tensão C-E
constante em VCEQ (a fim de eliminar o efeito Early) e variando iB
de um incremento DiB. Se iC variar em um incremento DiC:
O b do transistor (2)
DiC
h fe  b ca 
DiB
vCE = constante  vce = 0
 hfe: ganho de corrente
de curto-circuito.
Análises para pequenos
sinais: b = b ca (hfe).
Análise ou projeto de um
circuito de chaveamento:
b = b cc (hFE).
Observe que o valor de b
depende do nível de
corrente no dispositivo –
Figura 4.68.
vCE  constante
Figura 4.68 Dependência típica de b com IC e
com a temperatura em um moderno transistor npn
de silício empregado em circuitos integrados
projetado para operar em torno de 1 mA.
Os parâmetros H – quadripolos (Apênd. B)
Rede
linear de
dois
acessos
2 variáveis de excitação (ex: V1 e V2 )
2 variáveis de resposta (ex: I1 e I2 )
 A caracterização híbrida (ou parâmetros h) da rede de dois
acessos é baseada na excitação da rede por I1 e V2 (variáveis
independentes):
V1  h 11 I1  h12 V2
I 2  h 21 I1  h22 V2
 h11: a impedância de entrada no acesso 1 com o acesso 2 curto-circuitado
 h12: a razão de tensão reversa ou de realimentação da rede, medida com
o acesso de entrada em circuito aberto.
Os parâmetros H – quadripolos (2)
 h21: o ganho de corrente da rede com o acesso de saída curto-circuitado
(ganho de corrente em curto-circuito).
 h22: a admitância de saída com o acesso de entrada em circuito aberto.
Os parâmetros H – quadripolos (3)
FONTE: http://engphys.mcmaster.ca/~glen/2e4/lab6.pdf
- Equivalente Norton no acesso de saída;
- Equivalente Thevenin no acesso de entrada.
(1) hie: Impedância de entrada (Vin / Iin), quando Vout = 0 (em curto).
(2) hre: Relação entre a tensão de entrada e a tensão de saída (Vin / Vout),
forçando Iin a zero (circuito aberto).
(3) hfe: Ganho de corrente (Iout / Iin) com Vout = 0 (em curto).
(4) hoe: Condutância de saída (Iout / Vout) com Iin = 0 (circuito aberto).
Observação: correntes e tensões ac. Modelo linear  variações pequenas
em torno do ponto de operação.
Os parâmetros H – quadripolos (4)
FONTE: http://engphys.mcmaster.ca/~glen/2e4/lab6.pdf
Aplicações:
 Resistor série:
 TJB 2N3904 (polarizado com IC = 1 mA) – (configuração EC):
Os parâmetros H – quadripolos (5)
FONTE: http://engphys.mcmaster.ca/~glen/2e4/lab6.pdf
 Circuito amplificador integrado – Motorola, part # MC1590
(15 transistores, diodos e resistores – caracterização de quadripolo)
 Os parâmetros (Y) são complexos, de modo a levar em
consideração os efeitos das altas freqüências.
TJB: região de saturação – análise gráfica
Q
Reta de carga
Figura 4.69 Expansão da região de saturação das curvas características juntamente
com uma reta de carga que resulta na operação em um ponto Q na região de saturação
 Nesse caso, variações na corrente de base resultam em variações muito pequenas
em iC e vCE e o b incremental (bca) é muito pequeno.
A ruptura do transistor
As tensões máximas que podem ser aplicadas ao TJB são
limitadas pelos efeitos de ruptura nas junções EB e CB
(mecanismo de avalanche).
Configuração BC: Característica iC – vCB (Figura 4.63) 
Para iE = 0 (emissor em aberto), a junção CB se rompe para
uma tensão denominada BVCBO (Breakdown Voltage between
Collector and Base with emitter Open). – Tipicamente,
BVCBO > 50V.
Configuração EC: Característica iC – vCE (Figura 4.65) 
Ruptura ocorre para uma tensão BVCEO (às vezes chamado de
tensão de manutenção LVCEO (sustaining voltage) –
Tipicamente, BVCEO é metade de BVCBO .
A ruptura do transistor (2)
Ruptura da JCB (configurações BC e EC) não é destrutiva,
enquanto a dissipação de potência no dispositivo for mantida
dentro de limites seguros.
Ruptura da JEB: A JEB rompe-se por avalanche para uma
tensão BVEBO muito menor que BVCBO . – Tipicamente, BVEBO
está na faixa de 6 a 8 V, e a ruptura é destrutiva  O b do
transistor é permanentemente reduzido.
Esta redução do b não é preocupante quando da utilização da
JEB como um diodo zener para gerar tensões de referência
em projetos de CIs.
A ruptura do transistor e a máxima dissipação de potência
admissível são parâmetros importantes no projeto de
amplificadores de potência.
A ruptura do transistor (3)
Exercício 4.42: Qual a tensão de saída do
circuito da figura se o BVBCO do transistor é
de 70V?
Resp: – 60 V
Capacitâncias internas no TJB
Lembrem-se que a junção pn exibe efeitos de armazenamento
de cargas que podem ser modelados como capacitâncias.
A capacitância de difusão ou de carregamento de base
Cde.
Quando o transistor está operando no modo ativo ou de
saturação, cargas devidas aos portadores minoritários são
armazenadas na região de base:
Constante do dispositivo,
dimensão de tempo
W2
Qn 
iC  t F iC
2 Dn
com
Aplicável a grandes sinais
tF: tempo de trânsito de base direto (forward base-transit time) 
Representa o tempo médio que um portador de carga (elétron) leva
para atravessar a base.  Tipicamente: faixa de 10 a 100 ps. (No
modo ativo reverso: tR >> tF ).
Capacitâncias internas no TJB (2)
W2
Qn 
iC  t F iC
2 Dn
iC: exponencialmente relacionada a vBE  Qn depende de vBE
da mesma forma  Efeito capacitivo não-linear.
Para pequenos sinais: capacitância de difusão Cde:
Cde
dQn
diC
IC

tF
 Cde  t F g m  t F
dvBE
dvBE
VT
A capacitância da junção base-emissor ou da camada de
O valor de Cje para tensão zero
depleção Cje :
C je 
C je0
 VBE
1 
 V0e
Tensão interna da JEB (tipicamente, 0,9 V)



m
Coeficiente de graduação da JEB
(tipicamente, 0,5)
Capacitâncias internas no TJB (3)
A capacitância da junção coletor-base ou de depleção C m:
No modo ativo de operação, a JCB está reversamente
polarizada e sua capacitância de junção ou de depleção:
Cm 
O valor de Cm para tensão zero
Cm 0
 VCB 
1 

 V0c 
m
Coeficiente de graduação da JCB
(tipicamente, 0,2 – 0,5)
Tensão interna da JCB (tipicamente, 0,75 V)
O modelo -híbrido para altas freqüências:
C = Cde + Cje : capacitância de EB (tipicamente, na faixa de
alguns pF até algumas dezenas de pF).
Cm: a capacitância de CB (tipicamente, na faixa de uma
fração de pF até alguns poucos pF).
O modelo -híbrido para altas freqüências
Resistência rm omitida (mesmo em freqüências médias, a reatância de Cm
é muito menor que rm.
Adicionou-se a resistência rx: para modelar a resistência do silício da
região de base entre o terminal de base B e um terminal de base interno
(ou intrínseco) fictício B’, que está posicionado exatamente sobre a
região do emissor.  Tipicamente, rx é da ordem de algumas dezenas de
ohm e seu valor depende do nível de corrente de uma maneira
relativamente complicada. Como rx << rp, seu efeito é desprezível em
baixas freqüências. No entanto, sua presença é importante em altas
freqüências.
Comportamento de chaveamento do TJB
FONTE: http://ece-www.colorado.edu/~bart/book/book/chapter5/pdf/ch5_6_2.pdf
td,1: initial delay time (carregamento da capacitância da JBE).
trise: tempo de subida da corrente de coletor.
td,2: delay time (descarregamento da capacitância da JBE – enquanto houver
carga significativa armazenada na região da base, a corrente de coletor
continuará a existir.).
A freqüência de corte
As especificações do TJB fornecidas pelo fabricante
normalmente não especificam o valor de C. 
Normalmente é fornecido o comportamento de b ou hfe em
função da freqüência. (Para determinar C e Cm, deve-se
deduzir expressões para hfe em função da freqüência em
termos dos parâmetros -híbridos).
I c  ( g m  sCm )V :
corrente de coletor de curto - circuito.
Figura 4.71 Circuito para determinar uma expressão para hfe(s)  Ic / Ib.
A freqüência de corte (2)
V  I b (r // C // Cm )
Impedância vista entre B’ e E
g m  s Cm
Ic
 h fe  
I b 1 / r  s (C  Cm )
Para as freqüência s em que este modelo é válido, g m   Cm :
g m r
b 0 Valor de b para baixas
freqüências
h fe 
 h fe 
1  s (C  Cm ) r
1  s (C  Cm ) r
A freqüência de corte (3)
h fe 
b0
1  s (C  Cm ) r
 b 
T  b 0 b
: Resposta de pólo simples com uma
freqüência de corte em  = b.
1
C  Cm  r
: freqüência de ganho
unitário.
gm
 T 
C  Cm
gm
 fT 
2 C  Cm 
 A faixa de passagem de ganho unitário
fT é usualmente incluída pelo fabricante
do transistor em suas especificações
(tipicamente na faixa de 100 MHz até
dezenas de GHz).
A freqüência de corte (4)
 Em alguns casos, fT é fornecida em função de IC e VCE.
gm: diretamente proporcional a IC ;
C: apenas uma parte (a capacitância de difusão Cde) é diretamente
proporcional a IC .
fT diminui para baixas freqüências.
Diminuição de fT para altas correntes: mesmo fenômeno que reduz b0
para altas correntes.
Na região em que fT é praticamente constante: C é dominada pela
componente de difusão.
A freqüência de corte (5)
Observações importantes:
• O modelo -híbrido da figura 4.71 caracteriza a operação do
transistor com razoável precisão até freqüências de cerca de 0,2 T.
• Para freqüências mais altas deve-se adicionar outros elementos
parasitários no modelo, além de refinar esse modelo para considerar
que o transistor se torna uma rede de parâmetros distribuídos que
estamos tentando modelar através de um circuito com componentes
concentrados.
• No modelo da figura 4.71, para freqüências acima de 5 a 10 b,
pode-se ignorar a resistência r.  Nesse caso, rx torna-se a única
parte resistiva da impedância de entrada.  Uma determinação
precisa de rx deve ser feita a partir de medidas em altas freqüências.
A resposta em freqüência do
amplificador EC
Figura 5.71 (5a edição) (a) Amplificador EC acoplado por capacitores. (b) Esboço da
magnitude do ganho do amplificador EC pela freqüência. O gráfico define três bandas de
freqüência relevantes à determinação da resposta em freqüência.
Figura 5.72 (5a edição) Determinação da resposta em alta freqüência do amplificador EC: (a)
circuito equivalente; (b) o circuito em (a) simplificado tanto no lado de entrada quanto no lado de
saída; (c) circuito equivalente com Cm substituído no lado da entrada pela capacitância
equivalente Ceq; (d) esboço do gráfico da resposta em freqüência, a qual é a resposta de um
circuito passa-baixas STC (constante de tempo única).
Figura 5.73 (5a edição) Análise da resposta em baixa freqüência do amplificador
EC: (a) circuito amplificador com as fontes dc removidas; (b) o efeito de CC1 é
determinado assumindo-se que CE e CC2 atuam como curtos perfeitos;
Figura 5.73 (Continuação) (c) o efeito de CE é determinado assumindo-se que CC1 e
CC2 atuam como curtos perfeitos; (d) o efeito de CC2 é determinado assumindo-se que
CC1 e CE atuam como curtos perfeitos;
Figura 5.73 (Continuação) (e) esboço do ganho em baixas freqüências
assumindo-se que CC1, CE e CC2 não interaem e que suas freqüências de
quebra (ou pólos) encontram-se bastante separados.