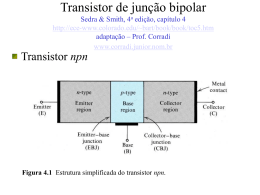
Estudos dos Transistores
Tivemos a oportunidade de acompanhar com detalhes, a construção e aplicações
do elemento PN, o que tornará simples a compreensão desta parte.
Consideremos duas junções PN polarizadas como segue:
Como podemos notar, a junção 1 está diretamente polarizada, enquanto que a
junção 2, acha-se reversamente polarizada. A junção 1 estando diretamente polarizada, terá
uma corrente (Id) de portadores majoritários (positivos por convenção) enquanto que a
junção 2, estando reversamente polarizada, terá apenas a corrente devido aos portadores
minoritários (também positivos e localizados no lado N da junção), e representada por (Is).
Caso combinar ambas as junções de acordo com a representação a seguir, teremos
como resultado dois tipos de transistores, um NPN e outro PNP.
As representações anteriores nos dão uma idéia do que realmente ocorre, porém há
uma observação a fazer quanto a região intermediária, que deverá ser a mais estreita
possível, de modo a evitar a recombinação dos pares elétron-lacuna. Passamos então a
representação a seguir, que nos dá os elementos NPN e PNP já polarizados com os
respectivos sentidos de tensão.
1
Considerações Gerais
E
B
C
IE
IB
IC
VBE
VCB
VEB
VBC
VCE
VEC
=
=
=
=
=
=
=
=
=
=
=
=
Emissor
Base
Coletor
Corrente de Emissor
Corrente de Base
Corrente de Coletor
Tensão Base-Emissor
Tensão Coletor-Base
Tensão Emissor-Base
Tensão Base-Coletor
Tensão Coletor-Emissor
Tensão Emissor-Coletor
Analisaremos ambos os transistores apresentados e seu funcionamento.
Tal qual no estudo dos díodos, existirá em cada junção do transistor uma barreira
de potencial. Podemos observar também que nosso elemento apresenta 3 terminais: o
Emissor, a Base e o Coletor. A junção Base-emissor será, em ambos os tipos, polarizada
diretamente e a junção Base-coletor será reversamente polarizada, o que facilmente
notamos nas duas ilustrações anteriormente apresentadas.
Ao polarizarmos diretamente a junção PN, teremos como já visto anteriormente
uma conseqüente redução da barreira de potencial e uma resistência de pequeno valor
devido à polarização direta desta junção. Ao polarizarmos reversamente a junção PN,
teremos um aumento na barreira de potencial e uma resistência de elevado valor devido a
tal polarização. Na ilustração a seguir, notamos claramente o acima exposto.
2
Faremos nosso estudo considerando elétrons como portadores majoritários,
portanto os portadores positivos já adotados em convenção terão sentido contrário ao dos
elétrons.
Os elétrons que são os portadores majoritários do material tipo N, correspondente
ao Emissor, são injetados na região da Base, devido à polarização direta da junção BaseEmissor. Como a junção Coletor-Emissor possui polarização inversa, os elétrons injetados
na região da Base provenientes do Emissor são atraídos para o Coletor, devido à elevada
tensão presente nos terminais do Coletor. Esse mecanismo de condução ficará melhor
compreendido se nos ativermos à figura seguinte.
P1 - Placa Polarizada Positivamente
P2 - Placa Polarizada Negativamente
e - Elétron
E - Campo elétrico formado no interior das placas.
Pela ilustração da figura 5, notamos que um campo elétrico (E) é formado no
interior de duas placas polarizadas, separadas por uma distancia d, e que esse campo dirigese do maior para o menor potencial. Uma carga negativa (1 elétron) colocada no interior
desse campo, dirigir-se-á ao ponto de maior potencial.
Se voltarmos agora ao transistor NPN, facilmente compreenderemos o fluxo de
corrente pelo mesmo.
Quanto à região da Base, comentamos que essa deveria ser a mais estreita
possível, de modo a diminuir a possível recombinação dos pares elétrons-lacuna. As
lacunas que se recombinarem com os elétrons, serão fornecidas por IB.
3
Resumo:
A junção Base-Emissor sendo diretamente polarizada, possue uma pequena
barreira de potencial, consequentemente pequena resistência, acelerando os elétrons em
relação a região da Base, que por sua vez é suficientemente estreita de modo a evitar as
recombinações dos pares elétrons-lacunas. As lacunas que possivelmente se recombinarem,
serão fornecidas por IB. O coletor sendo positivo em relação à Base, atrairá os elétrons nela
injetados, estabelecendo-se assim três fluxos de corrente: IE, IB e IC, de onde podemos
tirar as seguintes relações:
IE = IC + IB
e
VCE = VCB + VBE
Interpretação das expressões acima:
- Aplicando a Lei de Kirchhoff ao nó F, teremos que a corrente que entra num nó é
igual a corrente que sai. Logo, se entra IE e sai IB + IC, podemos concluir que IE = IC +
IB.
Como as baterias que determinam a polarização nas junções estão em série,
podemos somá-las, de modo que entre o Coletor e Emissor, teremos uma tensão
correspondente a soma das duas tensões VBE + VCB, obtendo a relação: VCE = VCB +
VBE.
A mesma análise pode ser feita para os transistores PNP.
Polarização de um Transistor NPN com Emissor aberto
Caso, tenhamos por algum motivo a representação abaixo, examinemos seu efeito.
Pelo que podemos notar, temos uma junção PN reversamente polarizada, de modo
que circulará pela mesma uma corrente devido aos portadores minoritários, como já visto
anteriormente, e denominada por ICO ou ICBO. Comumente é designada apenas por
corrente de fuga. O valor máximo da corrente ICO, para a temperatura ambiente é
especificada pelo fabricante do transistor. Para que tenhamos uma idéia do valor da mesma,
embora seja este função da temperatura e do tipo de transistor, daremos um exemplo
abaixo:
Para transistores de baixa potência, por exemplo de silício, ela assume valores em
torno de 0,0l µ A, enquanto que para elementos de germânio, assume valores da ordem de
l0 µ A à temperatura ambiente (250C). Podemos através de uma relação aproximada, uma
vez que ICO aumenta com a temperatura, afirmar o seguinte:
4
- A corrente ICO, dobra de valor para cada 100C de aumento da temperatura.
Consideremos o seguinte exemplo:
Um transistor apresentava uma corrente ICO de l0 µA na temperatura de 400C,
qual será o valor de ICO se o mesmo atingir 500C ?
Solução:
Se para cada 100C de aumento na temperatura ICO dobra de valor, passando de T1
= 400C para T2 = 500C, tivemos uma variação ∆T = T2 – T1 de 100C, logo a corrente
resultante será 2 x l0 µA = 20 µA . Concluímos, então, que a variação da temperatura é um
fator importante e deve ser controlada através do uso de dissipadores, assunto que
trataremos mais adiante. Até agora, representamos o transistor como um bloco, porém,
daqui em diante, passaremos a utilizar apenas símbolo, como vemos nas representações
seguintes:
Símbolos
Apesar de colocarmos os sentidos de corrente nos elementos NPN e PNP sem
termos uma polarização que determine a existência dos mesmos, isto deve-se apenas para
melhor interpretarmos os símbolos apresentados. Como regra prática, para identificarmos
qual elemento é NPN e qual é PNP, lancemos mão do seguinte artifício:
- Transistor NPN (Emissor Base Coletor)
Como adotamos por convenção que a corrente que circula é a de portadores
positivos (do elemento P para o elemento N), 1ogo ela sairá pelo Emissor, vinda da Base
(elemento P).
- Transistor PNP (Emissor Base Coletor)
5
Como adotamos por convenção que a corrente que circula é a de portadores
positivos (do elemento P para o elemento N), logo ela entrará pelo Emissor, indo para a
Base (elemento N).
Podemos notar pelos símbolos apresentados, que no Emissor existe uma flecha que
indica o sentido em que circula a corrente.
Configuração em que se apresentam os Transistores
Como podemos verificar pelas montagens apresentadas pelas figuras 8 e 9, temos
três circuitos básicos, que na ordem são:
Configuração Emissor Comum, Base Comum e Coletor Comum. Representamos
as três configurações para os transistores NPN e PNP. O tipo de configuração está
relacionado com o terminal de entrada e saída, e o termo Comum deve-se ao fato de que,
em cada configuração, possuímos um elemento Comum à Entrada e à saída .
Cada configuração, como podemos notar na figura 10, apresenta características
diferentes com relação às outras, resultando com isso diversas oportunidades de escolha
relativas a uma dada situação.
Configuração
E.C.
B.C.
C.C.
Características
Gi
elevado
<1
elevado
Gv
elevado
elevado
≤1
Rin
média
baixa
muito elevada
Fig. 10
E.C - Emissor Comum
B.C - Base Comum
Gv - Ganho de Tensão
Rin - Resistência de Entrada
6
Rout
alta
alta
muito baixa
C.C - Coletor Comum
Gi - Ganho de Corrente
Rout - Resistência de Saída
A tabela da figura 10 será utilizada quando tratarmos da parte relativa a casamento
de impedância dos diversos estágios amplificadores, por enquanto exemplifica a
diferenciação dos três tipos de montagens.
Correntes de Fuga do Transistor
Como podemos notar pela figura 11, teremos 3 situações distintas para o transistor,
Coletor Aberto, Base Aberta e Emissor Aberto. Verificamos também, que nos três casos
temos uma junção PN inversamente polarizada, logo teremos portadores minoritários
circulando pela junção, assunto já abordado na parte referente a junções PN.
Analisemos rapidamente cada uma das três situações:
a) Fig. 11a
IEBO - Corrente entre emissor e base com coletor em aberto: Não é normal termos tal
situação, uma vez que a junção Base-Emissor de um transistor é sempre
polariza da diretamente.
b) Fig. 11b
ICEO - Este componente ao contrário do anterior é de elevado significado, e para tanto
expresso em termos de β e ICBO, I CEO = (1 + β )I CBO . Embora não tenhamos
definido o parâmetro β , rapidamente podemos dizer que o mesmo determina a
amplificação de um circuito, e que será detalhado completamente nas partes
seguintes.
c) Fig. 11c
ICBO - Este componente varia com a temperatura, apresentando valores maiores para
transistores de germânio e valores menores para transistores de silício.
7
Considera-se de um modo geral, que este componente dobra de valor para cada
100C de aumento na temperatura assunto já abordado anteriormente.
Tensão de Ruptura de um Transistor
Fig. 12a
Fig. 12b
Fig. 12c
BVCBO - Tensão de ruptura entre Coletor e Base quando o Emissor está aberto.
BVCEO - Tensão de ruptura entre Coletor e Emissor quando a Base está aberta.
BVCES - Tensão de ruptura entre Coletor e Emissor quando a Base está ligada ao Emissor.
Num transistor, quando aplicarmos uma tensão inversa na junção Coletor-Base, a
condição de ruptura corresponde à ruptura de um díodo sob polarização inversa, assunto já
detalhado na parte referente à polarização inversa de uma junção PN. De um modo geral, a
tensão de ruptura depende do circuito, por segurança, nunca devemos ultrapassá-la.
Gostaria de frisar que o fabricante do elemento em estudo fornece todas as
informações possíveis sobre o mesmo, incluindo uma série de outras ainda não citadas,
como teremos oportunidade de verificar mais adiante.
Até o presente momento, para polarizarmos um transistor utilizamos duas baterias,
o que é anti-econômico do ponto de vista prático, de modo que de agora em diante,
passaremos a polarizá-lo com uma única fonte.
Polarização utilizando apenas uma Fonte
Configuração Emissor-Comum
8
Como podemos notar nas figuras 13a e 13b, com uma única fonte conseguimos
polarizar nosso transistor. Por simples análise do circuito, chegaremos às seguintes
relações:
Transistor NPN
IE = IB + IC, para tanto basta analisarmos o que ocorre no nó F, aplicando a Lei
de Kirchhoff:
- A soma das correntes que chegam a um nó é igual a soma das que saem.
Aplicando a Lei de Kirchhoff ao nó G, teremos
I4 = I1 + I2 + I3
Se aplicarmos o mesmo raciocínio ao nó F, teremos (fig.13a):- Chega ao nó F a corrente IE, saindo do mesmo IB + IC, logo IE = IB + IC.
VCE = VBE + VCB, esta é outra expressão de fácil compreensão pois as tensões VBE e
VCB, acham-se no mesmo sentido, e como tal podemos somá-las resultando portanto que
VBE + VCB = VCE.
Antes de prosseguirmos com comentários acerca do circuito da figura 13a,
gostaríamos de recordar determinados detalhes que facilitarão o completo entendimento do
mesmo.
Pela convenção de elemento passivo (Receptor) temos que:
- Corrente e tensão num receptor terão sentidos contrários.
- A seta da tensão indica o ponto de maior potencial.
- Pela Lei de ohm, VAB = RAB x I.
Outro detalhe refere-se ainda a Lei de Kirchhoff, que diz o seguinte:
9
A somatória das tensões em uma malha fechada será igual a zero, o que
provaremos com a maior facilidade, conforme o exemplo da figura 16.
Pela Lei de Ohm
VR1 = Rl x I
VR2 = R2 x I
Como podemos notar, VR1 e VR2 estão no mesmo sentido, e quando somadas
resultarão:
VRI + VR2 = VAB.
Se adotarmos um sentido de percurso para a malha da figura 16, notaremos o
seguinte:
- VCC e VAB estão em oposição de sentidos, logo quando somadas anular-se-ão.
Com essas considerações, podemos voltar ao circuito da figura 13a.
Passemos então a determinar as equações das malhas I e II.
Equação da Malha I
As tensões VAC, VCE e VRE acham-se no mesmo sentido, e quando somadas
resultarão no valor de VCC.
VCC = VRC + VCE + VRE
VCC = RC x IC + VCE + RE x IE
Equação da Malha II
Utilizando o mesmo raciocínio teremos:
VRB = VCB + VRC
RA x IB = VCB + RC x IC, onde VCB sai da relação VCB = VCE - VBE
10
Equação da Malha Externa
VCC = VRB + VBE + VRE
VCC = RB.IB + VBE + RE.IE
Tais expressões também podem ser obtidas para o elemento PNP e para todos as
outras configurações de modo análogo ao já citado, cujo objetivo foi demonstrar que com
uma única fonte podemos obter diferentes tensões em diferentes pontos, o que fica
evidenciado pelas equações de malha apresentadas.
Configuração Base Comum
Configuração Coletor Comum
Obs.:- A configuração Coletor-Comum também é denominada de seguidor de Emissor.
Tipos de Polarização
Daremos a seguir circuitos básicos utilizados na polarização de transistores.
a) Polarização com Corrente de Emissor Constante
11
Como já comentamos anteriormente, a variação na temperatura implica na
variação de IC, e consequentemente IE. Para que a mesma mantenha-se constante,
introduzimos no circuito o resistor RE, que embora reduzindo o ganho estabiliza em parte a
corrente IE.
b) Polarização com corrente de emissor constante e divisor de tensão na base.
c) Polarização com corrente de emissor constante e realimentação negativa na base.
Quando num circuito fazemos uma realimentação negativa, o ganho é reduzido,
porém ganha-se em estabilidade.
12
Definição dos Parâmetros alfa e beta
O parâmetro α é a relação entre a Corrente de Coletor e a Corrente de Emissor,
determinando a eficiência do mesmo.
α=
IC
IE
(eficiência)
O parâmetro β é a relação entre a Corrente de Coletor e a Corrente de Base,
sendo o ganho em C.C.
β=
IC
IB
(ganho de C.C.).
Obs.:
O parâmetro β é definido apenas para a montagem Emissor-Comum.
Podemos então expressar o parâmetro β em função de α , como segue:
- Do transistor tiramos a relação: IE = IC + IB
IC
→ IC = β ⋅ IB
- O parâmetro β é definido como: β =
IB
IC
IC
→ IE =
- O parâmetro α é definido como: α =
IE
α
(1)
(2)
(3)
Substituindo (2) e (3) em (1), temos:
IC
= βIB + IB .
α
(4)
Substituindo (2) em (4) temos
βIB
= βIB + IB ,
α
βIB
= IB(1 + β ) ,
α
β
α=
.
β +1
E, por processo análogo, determinamos a expressão de β em função de α , logo
teremos:
β=
α
.
1−α
13
Processos para Polarização de um Transistor
Daremos a seguir, um processo analítico para determinação de um ou mais
elementos relativos à polarização de um transistor.
Nota:
Este processo é apenas uma ferramenta auxiliar, pois finda a parte teórica,
introduziremos aos poucos recursos práticos utilizando as curvas do transistor, parâmetros
de estabilidade e outros que facilitarão a correta polarização do transistor. Esta parte agora
introduzida visa dar ao leitor alguma prática na solução de equações de malha, de grande
ajuda no processo final de polarização e projetos.
Para o circuito da figura 22, determinar os seguintes valores :
a) RC
b) RB
Dados
VCC = 12 Volts
IB = 20 µ A
β = 100
VCE = 4 Volts
RE = 800 Ω
VBE = 0,6 Volts
Obs.:No momento, não nos preocuparemos com o fato de determinados valores de
componentes utilizados, serem ou não serem comerciáveis, pois, estamos apenas de um
modo simples tentando recordar o processo de análise de malhas, Lei de Ohm, Leis de
Kirchhoff que já temos certeza de que o leitor conheça. Portanto, não estranhem se o valor
de RC, RB, RE, etc., calculados não se encontrarem dentro de padrões comerciáveis, pois
nosso objetivo será aos poucos encaminhar o leitor a decisões, e não simplesmente habituálo a cópias.
14
Resolução do Exercício
Você verá como é simples a resolução do mesmo, para tanto leia com atenção cada
parte em desenvolvimento.
Equação da Malha I
- A somatória de tensões em uma malha fechada é igual a zero. Aplicando esta
definição à malha I, teremos:
VCC - VRC - VCE - VRE = 0.
(1)
Ainda podemos escrever a equação (1) como:
VCC = VRC + VCE + VRE
(2)
Sabendo que:
VRC = RC.IC e VRE = RE.IE,
então
VCC = RC.IC + VCE + RE.IE
(3)
De uma simples análise da equação (3), verificamos os elementos não conhecidos
e partimos em busca dos mesmos, portanto, teremos de determinar IC, RC e IE, pois os
demais são conhecidos.
Quando definimos o parâmetro β dissemos o seguinte:
β=
IC
.
IB
É o ganho em C.C, e com este parâmetro que é conhecido, pois o fabricante do
transistor o fornece para cada diferente elemento fabricado, temos:
IC = β ⋅ IB ,
e calculamos o valor de IC.
IC = 100.20.10-6 = 2 000. 10-6 = 2. 10-3 = 2 mA.
Do transistor, tiramos a relação seguinte já conhecida:
IE = 2 mA + 20 µ A, reduzindo à mesma grandeza para que possamos efetuar a
soma temos :
15
IE = 2.10-3 + 20.10-6 = 2.10-3 + 2.10-5
IE = 2. 10-3 (1,01) = 2,02.10-3 = 2,02 mA ≅ 2 mA.
Como podemos verificar, IE é aproximadamente igual a IC e isto verificar-se-á
sempre que o valor de β for maior ou igual a 100. Como regra geral, podemos adotar
sempre em nossos cálculos:
Para β ≥ 100, temos que IE ≅ IC.
Após calcularmos IC e IE, voltamos novamente a equação (3) e calculamos o valor
de RC.
Equação (3) : VCC = RC x IC + VCE + RE x IE
Facilmente verificamos ter uma equação com uma única incógnita, que é RC.
Determinemos então o valor do mesmo.
Isolando RC da equação teremos:
VCC - VCE - RE x IE = RC x IC
(VCC - VCE - RE.IE) /IC = RC = (12-4-800.2.10-3) / 2.10-3 = (12-4-1,6) / 2.10-3
RC = 6,4 . 103 / 2 = 3,2 K Ω .
Equação da Malha II
Por processo já descrito, temos:
VRB = VCB + VRC
RB.IB = VCB + RC.IC
(4)
(5)
Da mesma maneira que no caso anterior, partimos em busca dos elementos
desconhecidos, que no nosso caso são RB e VCB.
Lembrando da equação do transistor já conhecida temos:
VCE = VBE + VCB, de onde facilmente isolamos VCB
VCB = VCE - VBE = 4 - 0,6 = 3,4 Volts.
Novamente, voltamos a ter uma equação a uma incógnita e determinamos o valor
da mesma.
Equação (5) :
RB.IB = VCB + RC.IC
RB = (VCB + RC x IC) IB = (3,4 + 3,2.103.2.10-3) / 20.10-6
RB = (3,4 + 6,4) / 2.10-5 = 4,9.105 = 490 K Ω .
Desta forma, conseguimos determinar os valores de RC e RB, com relativa
facilidade.
Gostaríamos de frisar, que em poucas linhas poderíamos determinar IC, IE, RC e
RE, e que o fato de parecer tão extenso deve-se unicamente a abordagem nos mínimos
16
detalhes do processo de resolução do problema. Estude bem o mesmo, pois no exercício
que virá a seguir usaremos todas as considerações já enunciadas, e em poucas linhas, e com
facilidade, determinaremos os elementos que faltam.
Dados
VCC = 25 Volts
VCE = 5 Volts
RC = 4 K Ω
IB = 20 µ A
β = 200
VBE = 0,6 Volts
Calcular
RE e RB
Equação da Malha I
VCC = VRC + VCE + VRE
VCC = RC x IC + VCE + RE x IE
Da equação acima, falta determinarmos os valores de IC, IE e RE. Da teoria
temos:
IC = β .IB = 200.20.10-6 = 4000. 10-6 = 4 mA.
Para β ≥ 100, IE ≅ IC, logo IE ≅ 4 mA.
Cálculo de RE:
VCC = RC x IC + VCE + RE x IE
VCC = RC x IC - VCE = RE x IE → (VCC - RC x IC - VCE) / IE = RE
RE = (25 - 4.103.4.10-3 - 5) / 4.10-3 = (25-16-5) / 4.10-3 = 4 / 4.10-3 =1.103 = 1 K Ω .
17
Equação da Malha II
VRB = VCB + VRC
RB x IB = VCB + RC x IC
Da equação acima, falta determinarmos os valores de VCB e RB. Do transistor
temos:
VCE = VBE + VCB,
VCE - VBE = VCB = 5 - 0,6 = 4,4 V.
RB x IB = VCB + RC x IC
RB = (VCB + RC x IC) / IB = (4,4 + 4.103.4.10-3) / 20.10-6
RB = (4,4 + 16) / 2.10-5 = 10,2.105 = 1,02 M Ω ≅ 1 M Ω .
Existe outro modo mais simples de calcularmos RB, que é através da equação da
Malha externa.
Equação da Malha Externa
Se olharmos entre os pontos A e B da figura 23, temos: As 3 tensões VRB, VBE e
VRE estão no mesmo sentido, e quando somadas resultarão na tensão VCC, que é a tensão
aplicada entre os pontos A e B, logo teremos:
VCC = VRB + VBE + VRE
VCC = RB x IB + VBE + RE x IE a única incógnita é o RB, basta calculá-lo.
VCC - VBE - RE x IE = RB x IB
(VCC - VBE - RE x IE) / IB = RB = (25-0,6-103.4.10-3) / 20.10-6
RB = 10,2.105 = 1,02 M Ω ≅ 1 M Ω .
Exercício
Calcular:
RC, RE e RB
Dados:
VCC = 20 Volts
VCE = 3 Volts
Trans. de silício
18
β = 100
IB = 40 µA
RC = 4.RE
Equação da Malha I
VCC = RC.IC + VCE + RE,IE
IC = β .IB = 100.40.10-6 = 4000.10-6 = 4.103. 10-6 = 4.10-3A= 4.0 mA
Para β > 100, IE ≅ 4mA
VCC = RC.IC + VCE + RE.IE
 VCC = 4 RE.IC + VCE + RE.IC
RC = 4RE

 VCC = RE.IC (4 + 1) + VCE = 5.IC.RE + VCE
IE = IC

VCC - VCE = 5.IC.RE → (VCC - VCE) / 5.IC = RE = (20 - 3) / 5.4.10-3
RE = 17 / 2.10-2 = 17.102 / 2 = 8,5.102 = 850 Ω .
Como RC = 4.RE, temos: RC = 4.850 = 3400 Ω =3,4K Ω .
Equação da Malha Externa
VCC = VRB + VBE + VRE = RB.IB + VBE + RE.IE
VCC - VBE - RE.IE = RB.IB → (VCC - VBE - RE.IE) / IB = RB
RB = (20-0,6-850.4.10-3 ) / 40.10-6 = (20-0,6-3,4) / 4.10-5 = (16/4).105 = 400K Ω .
Método Prático para Polarização de Transistores com Divisor de Tensão na Base
Considerações
a)
Aqui vamos desprezar a influência da corrente de fuga ICBO devido ao seu
pequeno valor, e também pelo fato do tipo de polarização empregado compensar
termicamente o circuito.
b)
Considerando β ≥ 100, poderemos desprezar a influencia do pequeno valor de IB,
de modo que a equação:
19
IE = IC + IB ficará reduzida a IE ≅ IC
c)
Escolha da Alimentação do Circuito
Esta solução é das mais simples, pois dependerá unicamente do local a ser
empregado, onde podemos contar com fontes padronizadas.
d)
Determinação de IC
Normalmente o valor de IC é obtido em função da carga, ou escolhida de acordo
com instruções fornecidas pelo fabricante do transistor em suas publicações sobre
seu produto.
e)
Cálculo de VRE
Vamos considerar VRE como sendo 10% da tensão de alimentação, consideração
que garantir-nos-á uma estabilidade à variações de temperatura e ganho de
corrente β
VRE = 10%VCC = 0,1.VCC = RE.IE = RE.IC
0,1.VCC = RE.IE → RE = (0,1.VCC) / IE.
f)
Determinação de VBE
VBE dependerá do tipo de transistor, pois para os de Germânio seu valor será ≅
0,3V, e para os de Silício, seu valor será ≅ 0,6V.
g)
Cálculo de I
Embora esta aproximação que aqui faremos pareça grosseira, ela resultará em
valores práticos e de fácil cálculo para Rbl e Rb2 .
I = 10% IC = 0,1.IC
h)
Cálculo de Rb2
Pela equação de malhas III temos:
Rb2 . I = VBE + RE . IE
Rb2 = (VBE + RE . IE) / I
i)
Cálculo de Rbl
Pela equação da malha externa temos:
VCC = Rbl . I + Rb2 . I
Rbl = (VCC - Rb2 . I) / I
Rbl = VCC / I - Rb2
j)
Cálculo de VC
Aqui novamente faremos uma imposição, garantindo que VC seja ≥ 50% de VCC,
de modo que VC será ≥ 0,5.VCC
(Pode-se trabalhar com a condição VC = 0,5.VCC).
20
k)
Cálculo de RC
RC = VC / IC
Como VC = 0,5.VCC temos:
RC = 0,5.VCC / IC
1) Exemplo
De acordo com as considerações feitas, vamos supor seguinte situação:
- ICBO desprezível
- β = 100 (o que equivale a dizer IE = IC)
- VCC = 12V
- IC = 10 mA
a) Cálculo de RE
VRE = 10% VCC = 0,1.VCC = 0,1.12 = 1,2V
RE.IE = VRE
RE = VRE / IE = VRE / IC =1,2 / 10.10-3 = 1,2 . 102 = 120 Ω .
b) Determinação de VBE
Transistor de Silício
VBE = 0,6V
c) Cálculo de I
I = 10% . IC = 0,1.IC = 0,1.10.10-3 = 10-3 A = 1mA.
d) Cálculo de Rb2
Rb2 = (VBE + VRE) / I = (0,6 + 1,2) / 10-3 = 1,8.103 = 1,8 K Ω .
e) Cálculo de Rbl
Rbl = VCC / I - Rb2 = 12 / 10-3 - 1,8.103 = 103 (1,2 - 1,8) = 10,2K Ω .
f) Cálculo de VC
VC = 50% VCC = 0,5 x 12 = 6V.
g) Cálculo de RC
21
RC = 0,5 x VCC / IC = 6 / (10 x 10-3) = 0,6.103 = 600 Ω .
2) Exemplo
Dados
VCC = 9 Volts
β = 100
IC = 3mA
Transistor de Silício
a) Cálculo de RE
VRE = 10% VCC = 0,1 x VCC = 0,9 Volts
VRE = RE x IE onde IE ≅ IC, pois β ≥ 100
RE =
VRE 9 ⋅ 10 −1
=
= 3 ⋅ 10 2 = 300Ω
IE
3 ⋅ 10 −3
b) Determinação de VBE
VBE = 0,6Volts
c) Cálculo de I
I = 10% IC = 0,1 x 3mA = 0,3mA
d) Cálculo de Rb2
Rb2 =
VBE + VRE 0,6 + 0,9 1,5 ⋅ 10 3
=
=
= 5KΩ
I
0,3
0,3 ⋅ 10 −3
e) Cálculo de Rbl
22
Rb1 =
VCC
9
− Rb2 =
− 4 ⋅ 10 −3 = 30 ⋅ 10 3 − 4 ⋅ 10 3 = 26KΩ
I
0,3 ⋅ 10 −3
f) Cálculo de VC
VC = 50% VCC = 0,5 x 9 = 4,5 Volts
g) Cálculo de RC
RC =
0,5 ⋅ VCC 0 ,5 ⋅ 9
4 ,5
=
=
⋅ 10 3 = 1,5KΩ
−3
IC
3
3 ⋅ 10
3) Exemplo
Vamos supor agora RC conhecido e igual a 600
VCC disponível igual a 6 Volts
Transistor de Silicio
β ≥ 100
a) Cálculo de VC
VC = 50% VCC = 0,5 x 6 = 3 Volts.
b) Cálculo de IC
VRC = 50% VCC = 3 Volts.
VRC = RC x IC,
IC = VRC/RC = 3/600 = 5 x 10-3 = 5mA.
c) Cálculo de RE
VRE = 10% VCC = 0,1 x 6 = 0,6 Volts.
VRE = RE x IE
onde IE ≅ IC para β ≥ 100
RE = VRE / IE = 0,6 / 5.10-3 = 120 Ω .
d) Determinação de V
VBE = 0,6 V.
e) Cálculo de I
I = 10% IC = 0,1 x 5mA = 0,5mA.
f) Cálculo de Rb2
Rb2 = (VBE + VRE) / I = (0,6 + 0,6) / 0,5.10-3 = 2,4K Ω .
23
g) Cálculo de Rbl
Rbl = VCC / I - Rb2 = 6 / 0,5.10-3 - 2,4.103 = 9,6K Ω .
Fig. 27
Dados
PDRC = 25mW
PDRE = 5mW
Tr.Si e IC = 5mA
β ≥ 100
VCE = 6Volts
Calcular
RC, RE, Rbl e Rb2
a) Cálculo de RC
PDRC = RC x IC2
RC = PDRC / IC2 = 25.10-3 / 25.10-6 = 1 K Ω .
b) Cálculo de RE
IE ≅ IC, pois β ≥ 100
PDRE = RE x IE2;
2
-3
RE = PDRE / IC = 5.10 / 25.10-6 = 0,2.103 = 200 Ω .
c) Cálculo de VCC
VCC = RC x IC + VCE + RE x IE = 103 .5 . 10-3 + 6 + 0,2.103. 5. 10-3 = 12 Volts.
d) Cálculo de I
I = 10% IC = 0,1 x IC = 0,5mA.
e) Determinação de VBE
24
Tr.Silício, VBE = 0,6Volts.
f)
Cálculo de Rb2
Rb2 = (VBE + VRE ) / I = (0,6 + 1) / 0,5.10-3 = 3,2K Ω .
g)
Cálculo de Rbl
Rbl = VCC / I - Rb2 = 12 / 0,5.10-3 - 3,2.103 = 20,8K Ω .
Fig. 28
Dados
PDRC = 32mW
PDRE = 8mW
PCmãx = VCE.IC = 20mW ( Potência máxima dissipada no transistor)
IC = 4mA
β ≥ 100
Calcular
RC, RE, VCE e VCC
a) Cálculo de RC
PDRC = RC.IC2 → RC = PDRC / IC2 = 32.10-3 / 16.10-6 = 2.103 = 2K Ω .
b) Cálculo de RE
PDRE = RE.IE2 = RE.IC2 (para β ≥ 100)
RE = PDRE / IC2 = 8.10-3 / 16.10-6 = 0,5.103 = 500 Ω .
c) Cálculo de VCE
PCmáx = VCE x IC → VCE = Pcmáx / IC = 20.10-3 / 4.10-3 = 5 Volts.
25
d) Cálculo de VCC
VCC = RC x IC + VCE + RE x IE = 2.103 . 4.10-3 + 5 + 0,5.103 .4.10-3 = 15V.
Obs.:Até o presente momento, para a polarização do transistor, não fizemos menção
alguma quanto ao cálculo da potência dissipada nos resistores que compõem a polarização
do mesmo, porém, este fator é de relevada importância, pois na polarização de um
transistor, devemos levar em conta a potência que cada resistor irá dissipar, caso contrário
incorreremos no risco da danificação de um ou mais dos componentes da polarização.
6) Exemplo
Dados,
VCC = 12 Volts
VCE = 7 Volts
IB = 100 µ A
β = 100
Tr.Si
a) Cálculo de IC
IC = β x IB = 100.100.10-6 = 10-2 A = 10 mA.
b) Cálculo de RE
Da malha (I) temos VRE = VCC - VCE = 5 Volts.
RE x IE = RE x IC ( β =100) = 5 Volts.
RE = 5 / IC = 5 x 102 = 500 Ω .
c) Cálculo de Rb
Da equação de malhas (II), temos
26
VRb = VCE - VBE = 7 - 0,6 = 6,4 Volts.
RB.IB = 6,4 Volts → Rb = 6,4 / 10-4 = 64K Ω .
d) Cálculo da Potência Dissipada em RE
PDRE = RE x IE2 = RE x IC2 = 0,5.103 .100.10-6 = 50mW.
e) Cálculo da Potência Dissipada em Rb
PDRb = Rb.IB2 = 64.103.10-8 = 64.10-5 = 0,64mW.
Modelo de Ebers-Moll para Transistores
Faremos a seguir, de uma forma bem resumida, o estudo de um modelo geral do
transistor, que poderá ser utilizado para baixas freqüências ou polarização DC. Na figura
30, temos representada a convenção de Ebers-Moll para tensões e corrente para um
transistor NPN.
IEF = Corrente de Emissor Direta
IER = Corrente de Emissor Reversa
ICF = Corrente de Coletor Direta
ICR = Corrente de Coletor Reversa
IE = IEF + IER
IC = ICF + ICR

 q.VBE
IEF = IES  e KT −1 ,


(1)
onde a expressão (1) vem da física dos semicondutores, e os componentes da mesma têm o
seguinte significado:
27