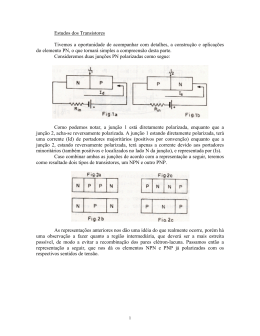
Transistor de junção bipolar
Sedra & Smith, 4a edição, capítulo 4
http://ece-www.colorado.edu/~bart/book/book/toc5.htm
adaptação – Prof. Corradi
www.corradi.junior.nom.br
Transistor npn
Figura 4.1 Estrutura simplificada do transistor npn.
Transistor de junção bipolar (2)
Transistor pnp
Figura 4.2 Estrutura simplificada do transistor pnp.
Dependendo da polaridade da tensão aplicada em cada
junção, obtém-se diferentes modos de operação do TJB.
Modos de operação do TJB npn
http://ece-www.colorado.edu/~bart/book/book/chapter5/ch5_3.htm e Sedra.
A função do emissor e do coletor
são invertidas (TJB não são normalmente
simétricos).
 “Ligado” – baixa impedância
 Saturado
 Liga/Desliga: circuitos lógicos
 “Desligado” – elevada impedância
 Amplificadores com TJB
 Cortado (vBC e vBE reversam. pol.)
 Pequena corrente reversa.
Modo
JEB
JCB
Cortado
Reverso
Reverso
Ativo
Direto
Reverso
Saturação
Direto
Direto
Operação do transistor npn na região ativa
Figura 4.3 Fluxo de corrente em um transistor npn polarizado de modo a operar na
região ativa. (Componentes de corrente reversa devido ao movimento de deriva de
portadores minoritários gerados termicamente não estão mostrados.)
 Estão mostrados apenas os componentes da corrente de difusão.
Concentração dos portadores minoritários
ncoletor = 0  JBC diretamente
polarizada
n p (0)  n p 0evBE / VT
Figura 4.4 Perfis das concentrações de portadores minoritários na base e no
emissor de um transistor npn operando no modo ativo: vBE > 0 and vCB  0.
A corrente de coletor iC
 Corrente de difusão de elétrons In :
 dn p ( x) 
 n p (0) 
  AE q Dn  

I n  AE q Dn 
 dx 
 W 
IS: fator de escala de corrente
 A corrente de coletor iC = In :
iC  I S e vBE / VT
 I S  AE q Dn
n p 0 (0)
W
ni2
 AE q Dn
W NA
 Observe que a magnitude de iC independe de vCB
(contanto que seja  0).
A corrente de base iB
 Componente iB1 (lacunas injetadas da base para a região do
emissor):
iB1 
AE q D p ni2
N D LP
e vBE / VT
Dp: difusividade das lacunas no emissor;
Lp: comprimento de difusão de lacunas no emissor;
ND: concentração de dopantes no emissor.
 Componente iB2 (lacunas que devem ser fornecidas pelo
circuito externo de modo a repor as lacunas perdidas na base pelo
processo de recombinação):
iB 2
1 AE q W ni2 vBE / VT


e
b 2 bN A
Qn
 b: tempo de vida do portador minoritário
Qn: carga do portador minoritário na base.
A corrente de base iB (2)
 iB  iB1  iB 2
 I S  vBE / VT
  e
b b
iC
 Dp N A W 1 W 2 

b  1 


D
N
L
2
D

n
D
P
n
b


 Constante para um transistor
em particular (no caso ideal)
b: ganho de corrente com emissor comum (usualmente,
100 < b < 200).
 Para obter um elevado valor de b (desejável), a base
deve ser fina (W pequeno) e levemente dopada e o
emissor fortemente dopado (NA / ND pequeno).
A corrente de emissor iE
 b  1
 b  1
vBE / VT
i

i

i

i

I
e




C
S
 E C B
b
b




iC  a iE
b
a
, a
, b
b 1
1a

I 
iE   S  evBE / VT
a 
a: constante para um transistor em particular
(idealmente), < 1 (se, por ex., b = 100  a  0,99).
 Pequenas variações em a correspondem a grandes
variações em b.
a: ganho de corrente em base comum.
Transistor npn na região ativa
Tensão direta vBE : corrente iC (dependência exponencial
com vBE ) flui no terminal de coletor.
iC independe da tensão do coletor contanto que vCB  0.
 Na região ativa de operação, o terminal de coletor
comporta-se como uma fonte de corrente constante
ideal, em que o valor da corrente é determinada por vBE .
iB = iC / b ; iE = i C + iB
iB << iC (b >>1)  iE  iC (iC = a iE , a < 1, mas  1)
Modelos de circuitos equivalentes
Diodo DE : fator de escala de corrente = IS / a  fornece a corrente
iE relacionada a vBE conforme as equações anteriores.
 Fonte de corrente não-linear controlada por tensão (grandes sinais).
Pode-se convertê-la em uma fonte de corrente controlada por
corrente expressando-se a corrente da fonte controlada por a iE.
B: terminal comum (terra)  a: ganho de corrente de E para C.
Estrutura física simplificada
Figura 5.6 Seção transversal de um TJB npn.
Fazer os exercícios 4.1 a 4.5 do livro texto.
O transistor pnp
Figura 4.7 Fluxo de corrente em um transistor pnp polarizado de modo a operar no
modo ativo.
O transistor pnp – circuitos
equivalentes (grandes sinais)
E
iE
+
vEB
iB –
DB
I S / b 
I S e vEB / VT
B
Figura 4.8 Dois modelos de grandes sinais para o transistor pnp operando no modo
ativo.
iC
C
Símbolos de circuito e convenções
iC
iE
 Indica a direção da
polarização direta da
junção BE.
Figura 4.10 Polaridade das tensões
e fluxo de corrente nos transistores
polarizados no modo ativo de
operação ( vBE (ou vEB ) >0 e vCB (ou
vBC )  0 ).
Relações corrente-tensão do TJB no
modo ativo de operação
iC  I S e
a
b
1a
vBE / VT
 I S  vBE / VT
iB     e
b b
a
iC
VT  tensão térmica 
 I S  vBE / VT
iE     e
a a 
iC
iB  1  a  iE 
iC  b iB
iE  b  1 iB
b 1
kT
q
 25 mV na temperatu ra ambiente
Obs: Para o transisto r pnp, substitua vBE por vEB .
iC  a iE
b
iE
b 1
Exemplo 4.1
O transistor na figura tem b = 100 e exibe uma tensão vBE de 0,7V
com iC = 1 mA. Projete um circuito de modo que uma corrente de 2
mA flua através do coletor e que uma tensão de + 5V apareça no
coletor.
Exemplo 4.1 - solução
VC = +5 V  VRC = 15 – 5 = 10 V
IC = 2 mA  VRC = 10 V / 2 mA = 5 kW
 vBE = 0,7 V com iC = 1 mA
 vBE com iC = 2 mA é dado por:
2
VBE  0,7  VT ln   0,717 V
1
 VB = 0  VE = – 0,717 V
b = 100  a = 100/101
 IE = IC / a = 2 / 0,99 = 2,02 mA
 RE = (VE – (– 15)) / IE = 7,07 kW
Representação gráfica das
características do transistor
iC  I S e vBE / VT
Figura 4.12 A característica iC –vBE de um transistor npn
(igual à curva i-v do diodo, exceto pelo valor da constante
n).
As características iE-vBE e iB-vBE são também
exponenciais, mas com diferentes correntes de escala: IS
/a para iE e IS /b para iB.
Para análises dc rápidas de primeira
normalmente assume-se que VBE  0,7V.
ordem,
Para um transistor pnp, a característica iC –vEB será
idêntica à da figura.
A tensão na junção emissor-base decresce de,
aproximadamente, 2 mV para cada acréscimo de 1oC na
temperatura (para uma corrente de junção constante).
Figure 4.13 Efeito da temperatura na característica iC–
vBE. Para uma corrente de emissor constante (linha
tracejada), vBE varia na taxa de –2 mV/C.
Transistor npn: i C  v CB (por iE)
Modo ativo de operação (vCB  0).
iC  a iE
Figura 4.14 A característica iC – vCB de um transistor npn.
Dependência de i C com a tensão de
coletor – o efeito Early
Modo ativo de
operação  TJBs
mostram uma certa
dependência com
da corrente de
coletor
com
a
tensão de coletor.
 Suas características
iC – vCB não são
linhas
retas
horizontais.
Figura 4.15 (a) Circuito conceitual para a medição da característica iC –vCE do TJB.
(b) A característica iC –vCE de um TJB usual.
Dependência de i C com a tensão de
coletor – o efeito Early (2)
vBE > 0.
vCE pequeno (vC < vB)  JCB:
polarização direta  região de
saturação.
 vCE  vCB < 0  JCB: pol.
reversa   espessura da região
de depleção na JCB   WEFETIVA DA
BASE   IS   iC : efeito Early.
 Relação linear de iC com vCE : assumindo que IS permanece constante:
iC  I S e
vBE / VT
 vCE 
1 

 VA 
 Inclinação não-nula das linhas
retas iC – vCE : a impedância de
saída do coletor não é infinita
Dependência de i C com a tensão de
coletor – o efeito Early (3)
Inclinação não-nula das linhas retas iC – vCE  a impedância de
saída do coletor é finita e definida por:
 i
ro   C
 vCE


vBE constante 

1
Da equação anterior: ro  VA / IC
IC : o nível da corrente correspondendo ao valor constante de
vBE próximo à fronteira da região ativa.
Esta dependência de iC com vCE no projeto e análise do circuito de
polarização normalmente não é considerada; no entanto, a
resistência de saída finita ro pode ter um efeito significativo no
ganho de amplificadores a transistores.
Análise dc de circuitos com transistores
Modelo da tensão constante VBE  assuma que VBE = 0,7V
independentemente do valor exato da corrente iC .
Exemplo 4.2: Considere o circuito da figura. Deseja-se analisar
este circuito de modo a determinar as tensões em todos os nós e as
correntes em todos os ramos. Assuma b = 100.
Exemplo 4.2 – análise
O transistor está na região ativa?
 VB (em relação ao terra) = 4V ; VE = VRE < 4V (assumindo o modo
ativo de operação, há uma queda VBE de 0,7 na JBE)  A junção
BE está diretamente polarizada.
 VE = 4 – VBE  4 – 0,7 = 3,3 V
 VRE = VE = 3,3 V  IE = VE / RE = 1 mA .
 VC = 10 V – IC RC ; VB = 4V
 Vamos assumir que VBC < 0: região ativa de
operação (juntamente com a condição VBE > 0).
 Assim: IC = a IE = b / (b+1) = 100/101  0,99
 IC = 0,991 = 0,99 mA.
 VC = 10 – IC RC = 10 – 0,99  4,7  +5,3 V: VBC = – 1,3V ()
Exemplo 4.2 – análise (2)
VBE > 0 , VBC < 0: O transistor está na região ativa?
 IB = IE / (b + 1) = 1 / 101  0,01 mA.
 Condições consistentes  O transistor está na região ativa!
Exemplo 4.3
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.
O transistor está na região ativa? Assuma, inicialmente, operação
na região ativa.
 O transistor está
no modo de saturação
(visto mais adiante).
Exemplo 4.4
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.
O transistor está na região ativa?  VB = 0V  JBE não conduz
(VBE < 0)  iE = 0 ; VC = 10  IC  4,7k > VB = 0  JBC não
conduz (VBC = 0 – VC < 0)  iC = 0  iB =  iC – iE = 0
 O transistor está no modo cortado de operação.
Exemplo 4.5
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.
Observe que o transistor agora é pnp!
Exemplo 4.6
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.
O transistor está no modo ativo?
Exemplo 4.7
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.
O transistor está no modo ativo?
Exemplo 5.9 – 5a edição do Sedra&Smith
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.
Exemplo 4.8
Analise o circuito da figura e determine as tensões em todos
os nós e as correntes em todos os ramos. Assuma b = 100.