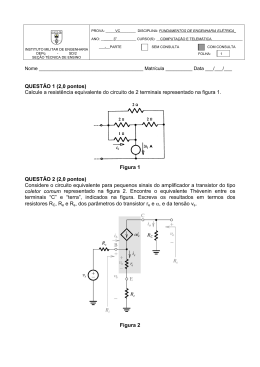
Estudo sobre as técnicas de
identificação de sistemas SISO
Nathali de Farias Ono -Bolsista de iniciação científica do CNPq - PIBITI
Prof. Dr. Alexandre Brincalepe Campo (orientador)
Prof. Dr. Álvaro Romanelli (co-orientador)
Centro Federal de Educação Tecnológica de São Paulo – CEFET-SP
Palavras-Chave: modelagem experimental, método determinístico, método de mínimos quadrados.
Objetivo
Método determinístico
Este trabalho tem como objetivo aplicar
métodos de identificação em sistemas dinâmicos
lineares que possuam uma entrada e uma saída
(SISO "Single-Input Single-Output").
Este método permite encontrar os parâmetros
da função de transferência de primeira ordem
através da medição de dois valores obtidos da
resposta transitória.
Introdução
As técnicas de identificação têm o propósito de
obter parâmetros a fim de encontrar um modelo
que represente o comportamento dinâmico do
sistema original.
Figura 7: Gráfico das respostas dos modelos com a aplicação do sinal de onda triangular
Figura 1: Etapas da modelagem experimental
Experimentos
Foram realizados experimentos com diversos
sistemas. Um sistema escolhido para a aplicação
dos métodos foi um circuito composto por dois
resistores e dois capacitores, em uma configuração
em cascata do tipo RC-RC. Na entrada do circuito
foram aplicados sinais de onda quadrada, de onda
triangular e de onda senoidal.
Figura 2: Circuito RC-RC
As amostras da entrada e da saída do circuito
foram recolhidas utilizando uma placa de aquisição
de dados e o software LabVIEW.
Foram construídas as respostas transitórias do
sistema utilizando o software MATLAB. As
respostas mostram que a função de transferência
possui características de um sistema sobreamortecido, ou seja, possui dois pólos reais e
diferentes, sendo que um deles é dominante no
comportamento da resposta transitória do sistema.
Figuras 4 e 5: Aplicação do método determinístico na resposta transitória
Método de Mínimos Quadrados
O Método de Mínimos Quadrados permite o
cálculo de uma aproximação do sistema de tal
forma a obter a melhor curva de aproximação
quando o erro envolvido é a soma dos quadrados
das diferenças entre os valores obtidos na
aproximação e os valores reais, sendo que o
Método de Mínimos Quadrados minimiza esse
valor. Este método foi aplicado com as amostras
adquiridas pelo circuito RC-RC através da
elaboração de um programa em linguagem
MATLAB.
Resultados
Os modelos calculados através dos métodos
acima descritos foram simulados com a aplicação
dos sinais reais de onda quadrada, onda triangular
e onda senoidal.
Figura 8: Gráfico das respostas dos modelos com a aplicação do sinal de onda senoidal
Através dos gráficos observa-se que os
modelos apresentam um comportamento dinâmico
muito próximo ao do sistema original, sendo que o
erro quadrático médio calculado foi muito
pequeno para todos os modelos construídos.
Outras aplicações
As técnicas de identificação apresentadas
também foram aplicadas em um circuito RLC com
características de um sistema sub-amortecido.
Conclusão
Os modelos obtidos pelo procedimento
experimental foram validados, comprovando que
as técnicas envolvidas são eficazes para identificar
parâmetros de um sistema SISO. Cabe lembrar
que os modelos são de grande utilidade prática,
pois poderão ser utilizados para o projeto dos
controladores dos sistemas dinâmicos.
Agradecimentos
A bolsista agradece ao CNPq pelo apoio
financeiro através do programa PIBITI.
Bibliografia
AGUIRRE,L.A. Introdução à Identificação de
Sistemas – Técnicas Lineares e Não-lineares
Aplicadas a Sistemas Reais. 2a. Edição: Belo
Horizonte. Editora UFMG, 2004.
Figura 3: Gráficos dos sinais de entrada e das respectivas respostas do sistema
Figura 6: Gráfico das respostas dos modelos com a aplicação do sinal de onda quadrada
OGATA, K. Engenharia de Controle Moderno.
4a. Edição: São Paulo. Pearson, 2003.