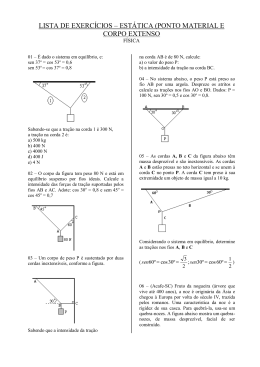
www.fisicaexe.com.br
Para o sistema em equilíbrio ao lado, determine as trações nas
cordas A e B sabendo que o corpo C tem 100,0 N.
Esquema do problema
As forças que agem no sistema são a força peso no
bloco C que aponta para baixo.
A corda A faz um ângulo de 60º com o teto, traçando
uma linha horizontal que passa pelo ponto onde está preso o
r
corpo C, temos que a tração T A também forma um ângulo de
60º com a horizontal, pois estes ângulos são alternos internos.
A corda B faz um ângulo de 60º com a parede vertical, o
r
ângulo entre a tração T B e a corda que prende o bloco C
também é 60º, estes ângulos são alternos internos, o ângulo
r
entre a linha horizontal onde está preso o corpo C e a tração T B
é de
30º com a horizontal, pois estes ângulos são
complementares, devem somar 90º.
figura 1
Dado do problema
•
peso do corpo C:
100,0 N;
Solução
Em primeiro lugar vamos decompor as forças que agem
no sistema em suas componentes num sistema de eixos
r
coordenados como mostrado na figura ao lado. A força peso P
r
tem apenas a componente P y ao longo do eixo y na direção
r
r
r
negativa; a tração T A possui as componentes T A x e T A y nas
direções de x positivo e de y positivo, respectivamente, e a
r
r
tração TB possui a componente T B x na direção de x negativo e
r
a componente T B y na direção de y negativo.
Como o sistema está em equilíbrio a resultante das
forças que agem sobre ele deve ser igual a zero, para isso
devemos ter
r
∑F = 0
direção x:
direção y:
r
r
− TBx + T A x = 0
r
r
r
− Py − T By + T A y = 0
em módulo teremos
−T B .cos 30° + T A .cos 60° = 0
− P − T B .sen 30° + T A .sen 60° = 0
1
figura 2
www.fisicaexe.com.br
com estas expressões podemos montar um sistema de duas equações a duas incógnitas (T A e
T B)
−
3
1
TB + T A = 0
2
2
1
3
− 100 − T B +
TA = 0
2
2
(I)
(II)
da equação (I) tiramos o valor de T A
1
3
TA =
TB
2
2
TA =
3 TB
substituindo (III) em (II) temos o valor de T B
3
1
. 3 TB = 0
− 100 − T B +
2
2
1
3
− T B + T B = 100
2
2
T B = 100 N
substituindo o valor encontrado acima em (III) obtemos o valor de T A
TA =
3 .100
T A ≅ 173 N
2
(III)