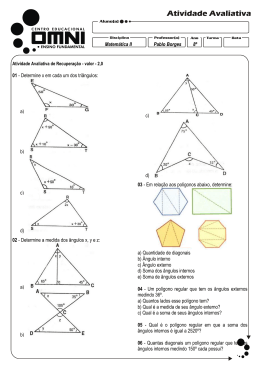
▼
Questão 62
Em um plano, é dado um polígono convexo de seis lados, cujas medidas dos ângulos internos, dispostas em
ordem crescente, formam uma progressão aritmética. A medida do maior ângulo é igual a 11 vezes a medida
do menor. A soma das medidas dos quatro menores ângulos internos desse polígono, em graus, é igual a
a) 315
b) 320
c) 325
d) 330
e) 335
Resolução
Sendo a a medida do menor ângulo, e r (r . 0) a razão da progressão aritmética citada no enunciado, temos:
(1)A soma das medidas dos seis ângulos do polígono é igual a (6 – 2) ⋅ 180°, ou seja, 720°. Assim, a soma dos
termos da progressão é:
(a + 11a) ⋅ 6
= 720° ∴ a = 20°
2
(2)a + 5r = 11a ∴ r = 2a
De (1) e (2), segue que r = 40°. Assim, as medidas dos ângulos desse polígono são:
20°, 60°, 100°, 140°, 180°, 220°.
Essas medidas contradizem o enunciado, uma vez que:
• as medidas dos ângulos internos de um polígono convexo são menores do que 180°.
• um polígono, convexo ou não, não pode ter um ângulo interno medindo 180°.
Assim, não existe um polígono nas condições do enunciado.
Sem resposta