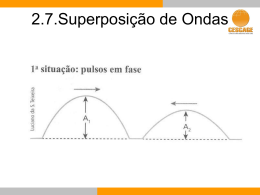
INTERFERÊNCIA
BIDIMENSIONAL
• Se 2 fontes de ondas bidimensionais
(fontes que produzem ondas na superfície
da água, por exemplo) produzirem ondas
coerentes (cada uma produz um pico e
um vale no mesmo instante), de mesma
frequência e amplitude, a superfície da
água será preenchida por ondas que
interferem provenientes das 2 fontes.
Teremos uma situação parecida com a da
figura a seguir.
Observa-se na figura as 2 fontes na parte inferior da mesma e a superfície da
água preenchida pelas ondas produzidas por ambas as fontes.
• Em algumas regiões da superfície do líquido os
picos e vales das ondas produzidas chegarão
sempre no mesmo instante, havendo, portanto,
nestas regiões, interferência construtiva.
• Em outras regiões chegarão simultaneamente o
pico de uma onda produzida por uma fonte e o
vale produzido pela outra. Nestas regiões ocorrerá
sempre interferência destrutiva.
• Visto de cima, teremos uma situação semelhante
a representada abaixo, onde os pontos escuros
representam as interferências construtivas
(chegada simultânea dos picos ou vales), e os
pontos claros representam as interferências
destrutivas (chegada simultânea dos picos de
uma fonte e vales da outra).
• Podemos expandir um pouco a figura anterior
para explorá-la um pouco mais. Observe a figura
a seguir.
• Nesta figura há linhas cheias unindo os pontos de
interferência construtiva. Estas são chamadas de linhas
ventrais. Nelas encontram-se os pontos Q e R, por
exemplo. Há também linhas pontilhadas (não as confunda
com as pontilhadas que representam os vales das ondas)
que unem os pontos de interferência destrutiva. Elas são
chamadas de linhas nodais e os pontos S e T, por
exemplo, estão sobre 2 delas.
• É possível estabelecer uma condição para determinarmos onde se
encontram os pontos de interferência construtiva e de interferência
destrutiva. Se você reparar bem, onde ocorrer interferência
construtiva, a diferença de caminho entre as ondas produzidas pelas
fontes 1 e 2 deverá ser sempre um múltiplo inteiro de λ (comprimento
de onda). Tente ver isso para os pontos R e P. No caso dos 2, qual a
diferença de caminho percorrido pelas 2 ondas?
• Para a interferência destrutiva, a condição é que a
diferença corresponda a um múltiplo ímpar de  .
2
Tente verificar isso para os pontos T e S.
•
De uma forma geral, temos a seguinte situação que podemos obter a partir da
figura abaixo:
Para que haja interferência construtiva, teremos que satisfazer a condição
que PF2 – PF1 = n(λ/2), onde n deve ser 0, 2, 4, 6,...par.... Para o caso do
ponto P, veja que n = 2.
•
Para a interferência destrutiva, devemos ter a diferença de caminho escrita da
seguinte forma: QF1 – QF2 = n(λ/2), onde n = 1, 3, 5, 7, ...ímpar. Observe que para
o caso do ponto Q, n = 3.
• Para ver se você compreendeu de fato,
tente resolver os 3 exercícios a seguir. A
resolução encontra-se mais a frente, mas
tente resolvê-los antes de seguir para a
solução.
Exercício 1
Exercício 2
Exercício 3
SOLUÇÕES
Solução do exercício 1.
Solução do exercício 2.
Solução do exercício 3.
Exercícios resolvidos e algumas figuras retiradas do site:
http://www.ciencia-cultura.com/Pagina_Fis/vestibular00/vestibular_IntroduOndulatoria003.html