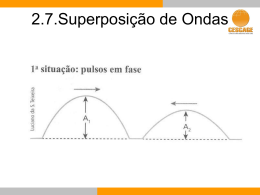
Ondulatória
Revisão -5- Ondulatória
Interferência
Superposição de Ondas
a
Pelo princípio da Superposição de Ondas cada ponto tem uma
amplitude igual à soma algébrica das amplitudes dos pulsos
componentes, ou seja:
a = a1 + a2
Revisão -5- Ondulatória
Superposição de Ondas
Agora os pulsos estão em oposição de fase e a superposição ocorre no
ponto P.
De acordo com princípio da superposição, no ponto P, tem-se:
a = a1 - a2
Revisão -5- Ondulatória
Ondas Estacionárias

2
Nó
Nó
Ventre
Nó
Ventre

2
Em uma onda estacionária não há o transporte de
energia. A distância entre nodos ou ventres sucessivos
correspondem a meio comprimento de onda  .
2
Revisão -5- Ondulatória
Interferência
Nas regiões em que há interseção de duas linhas cheias (duas cristas) ou
de duas linhas tracejadas (dois vales) tem-se uma interferência construtiva.
Na superposição de uma linha cheia (crista) com uma linha tracejada (vale)
obtém-se uma interferência destrutiva.
Ponto (A)  Interferência Construtiva
Ponto (B)  Interferência Destrutiva
Revisão -5- Ondulatória
Condições de Interferência
Fontes F1 e F2 emitindo ondas em fase.
Fonte 1
d1
d2
Fonte 2
Como as fontes estão em
fase no ponto P tem-se uma
interferência, construtiva ou
destrutiva se:
d = n

2
d=d2-d1 (diferença de caminho)
Para n(par) n=0,2,4,6... a interferência é construtiva.
Para n(ímpar) n=1,3,5,7... A interferência é destrutiva.
Revisão -5- Ondulatória
Fontes F1 e F2 emitindo ONDAS EM OPOSIÇÃO DE FASE
Fonte 1
d1
d2
d = n

2
Fonte 2
d=d2-d1 (diferença de caminho)
Para n(par) n=0,2,4,6... a interferência é destrutiva.
Para n(ímpar) n=1,3,5,7... A interferência é construtiva.
Revisão -5- Ondulatória
Batimentos
Agora observe a superposição de duas ondas de
freqüências f1 e f2 muito próximas uma da outra.
Cada passagem
da amplitude
resultante por um
máximo ou por
um mínimo
denomina-se de
batimento.
Freqüência resultante do batimento
f1  f 2
2
O número de batimentos na unidade de tempo (N) é igual a diferença entre as
freqüências das ondas que se superpõem.
fr 
N=|f1-f2|