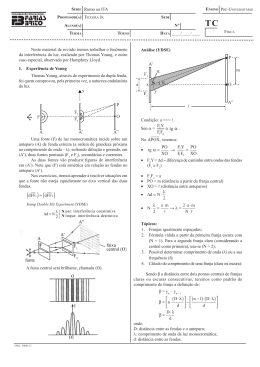
Capítulo 36
Interferência
36.1 Interferência
Luz solar (branca)
composta (cores)
Bolha de sabão
Arco-íris
=
refração
interferência
Interferência  superposição
construtiva
destrutiva
Óptica ondulatória
Aplicações
Filmes anti-reflexivos para
lentes, espelhos dielétricos,
filtros de interferência, etc
36.2 A luz como uma onda
Christian Huygens (1678)
teoria ondulatória
Princípio de Huygens:
Frente de onda
Fontes pontuais
Nova frente (tangente)
A lei da refração
l1
e
q1
h
l2
l1
q1
l2 q2
g
q2
c
A lei da refração
Definição índice de refração:
Nosso caso:
ou
Lei de Snell
Verificação
A figura abaixo mostra um raio de luz monocromática atravessando
um material inicial (a), materiais intermediários (b) e (c) e voltando
a atravessar um material a. Coloque os materiais na ordem das
velocidades com que a luz se propaga em seu interior, da maior
velocidade para a menor.
a
b
c
a
Comprimento de onda e
índice de refração
l varia
Veloc. varia
veloc.
n
E a freqüência?
não muda!
Relembrando:
Interferência  superposição
construtiva
destrutiva
Depende da fase
dif. caminhos ópticos  dif. de fase
Diferença de caminho óptico
n2
n1
L
N
número de l no meio
Diferença de caminho óptico
n2
n1
n2 > n1
L
Diferença de caminho óptico
n2
n1
N
número de l no meio
L
Destrutiva
(p)
Construtiva (2p)
Verificação
As ondas luminosas dos raios da figura abaixo têm o mesmo
comprimento de onda e estão inicialmente em fase. (a) Se o material
de cima comporta 7,60 comprimentos de onda e o material de baixo
comporta 5,50 comprimentos de onda, qual é o material com maior
índice de refração? (b) Se os raios luminosos forem levemente
convergentes, de modo que as ondas se encontrem em uma tela
distante, a interferência produzira um ponto muito claro, um ponto
moderadamente claro, um ponto moderadamente escuro ou um
ponto escuro?
n2
n1
L
36.3 Difração
onda + obstáculo = difração
Sem distinção entre interferência e difração
Pelo princípio de Huygens
http://www.paulisageek.com/school/cs348b/HuygensDiffraction.jpg
36.4 O experimento de Young
Thomas Young (1801)
luz é onda
sofre interferência
- mediu lméd = 570 nm luz solar (hoje 555 nm)
O experimento de Young
Figura de interferência
A localização das franjas
q
D
D >> d
S1
q
q
q
d
tela
q
S2
Intensidade

DL
DL
(franjas claras)
(franjas escuras)
A localização das franjas
Verificação
Na figura abaixo, qual é o valor de DL (em número de comprimentos
de onda) e a diferença de fase (em comprimentos de onda) para os
dois raios se o ponto P corresponde (a) a um máximo lateral de
terceira ordem e (b) a um mínimo de terceira ordem?
q
D
D >> d
S1
q
q
q
d
tela
q
S2
DL
ordem
(franjas claras)
(franjas escuras)
Exercícios e Problemas
36-14E. Em um experimento de Young, a distância entre as
fendas é de 100 vezes o valor do comprimento de onda da luz
usada para iluminá-las. (a) Qual é a separação angular em
radianos entre o máximo de interferência central e o máximo
mais próximo? (b) Qual é a distância entre estes máximos se a
tela de observação estiver a 50,0 cm de distância das fendas?
36.5 Coerência
interferência
coerência
intensidade das franjas
Fontes coerentes
Maioria das fontes
dif. de fase não varia com t
parcialmente coerentes (ou incoerentes)
Sol: parcialmente coerente
Laser: coerente
Exp. de Young: 1a. fenda essencial se fonte não coerente
36.6 Intensidade das franjas de
interferência
No ponto P:
dif. de fase
fonte
Se f = cte.
ondas coerentes
Campo elétrico, representação
senoidal e fasores
http://en.wikipedia.org/wiki/File:Unfasor.gif
Combinando campos: fasores
w
w
+
w
=
E
b
b
2b = f (ang. ext.)
Como:
Logo:
intens. por apenas 1 fenda
Onde:
dif. de
fase
dif. de
dist. percorrida
Máximos em:
Então:
Ou:
Mínimos em:
Ou:
I
5p
2
2
p
3p
1
1
0
4I0
0
0
p
3p
1
0
2
1
2
2,5 2 1,5 1 0,5 0 0,5 1 1,5 2 2,5
Se fontes incoerentes f
Interferência

f
5p
m máx.
m mín.
DL/l
f(t)  I = 2 I0 (toda tela)
não cria nem destrói energia luminosa
Coerentes ou não
Imed = 2 I0
+ de 2 ondas ?
w
Usar fasores !!!
Verificação
Cada um dos quatro pares de ondas luminosas chega num certo
ponto de uma tela. As ondas tem o mesmo comprimento de onda.
No ponto de chegada, suas amplitudes e diferenças de fase são
(a) 2E0, 6E0 e p rad; (b) 3E0, 5E0 e p rad; (c) 9E0, 7E0 e 3p rad;
(d) 2E0, 2E0 e 0 rad. Ordene de forma decrescente os quatro
pares segundo a intensidade da luz nesses pontos.
Exercícios e Problemas
36-27P. S1 e S2 na Fig. 36.29 são fontes pontuais de ondas
eletromagnéticas com um comprimento de onda de 1,00 m. As
fontes estão separadas por uma distância d = 4,00 m e as ondas
emitidas estão em fase e têm intensidades iguais. (a) Se um detector
for deslocado para a direita ao longo do eixo x a partir da fonte S1, a
que distância de S1 serão detectados os três primeiros máximos de
interferência? (b) A intensidade do mínimo mais próximo é
exatamente zero? (Sugestão: O que acontece com a intensidade da
onda emitida por uma fonte pontual quando nos afastamos da
fonte?)
S1
x
d
S2
Fig. 36.29
a)
36.7 Interferência em filmes finos
Cores
interf. reflex. 2 interfaces
Espessura aprox. comprim. de onda (l)
Espessura >
 coerência < (da fonte)
r2
refletido 1
n2
n1
n3
incidente
r1
q
refletido 2
filme
q
c
b
a
i
transmitido
Claro ou escuro?
Se r1 e r2 em fase
Se r1 e r2 fora de fase
L
clara
escura
Se q  0
dif. de caminho  2L
So saber 2L não basta!
1) DL em meio diferente do ar  dif. l
2) Reflexão  mudança fase ?
Mudanças de fase causadas por
reflexão
Refração
Reflexão
fase não muda
fase pode mudar ou não
antes
depois
antes
depois
Caso da óptica:
Reflexão
Meio com n menor
Meio com n maior
mudança de fase
0
0,5 l
(ou p)
Retomando a figura:
r2
n2
n1
n3
r1
q
q
i
c
b
não inverte
a
inverte
Supondo: n2 > n3 e n2 > n1 !!!!
Equações para a interferência em
filmes finos
f causado por:
1. Reflexão 1 das ondas
2. Diferença de percurso
3. Propagação em meios com n diferentes
Supondo: n2 > n3 e n2 > n1 !!!!
Reflexão
Dist. percorrida
n dist. Percorrida
r1
0,5 l
r2
0
2L
n2
Equações para a interferência em
filmes finos
 Em fase: 2L=(número impar/2) (l/n2)
fora:
2L=(número inteiro) (l/n2)
Logo:
(max-claro)
(min-escuro)
ATENÇÃO: Ainda supondo: n2 > n3 e n2 > n1 !!!! Caso contrário as
equações podem ser invertidas.
Exercícios e Problemas
36-34E. Uma lente com índice de refração maior que 1,30 é
revestida com um filme fino transparente de índice de refração 1,25
para eliminar por interferência a reflexão de uma luz de
comprimento de onda l que incide perpendicularmente a lente.
Qual é a menor espessura possível para o filme?
36.8 O interferômetro de
Michelson
1881
1o. modelo de interf.
Esquemático
M2
Despreza-se a espessura de M
Dif. de trajeto: 2d2 – 2d1
Se existe meio L, n no caminho:
d2
s
M
(meio)
M1
d1
(antes)
observador
Mud. de fase l
desl. 1 franja
Metro: linha do tempo
•1790 — A Assembléia Nacional da França decide que a medida do novo metro seria igual a medida do
comprimento de um pêndulo com a metade do período com duração de um segundo.
•1791 — A Assembléia Nacional da França aceita a proposta da Academia Francesa de Ciências da nova definição
do metro ser igual a um décimo de milionésimo do comprimento do meridiano terrestre ao longo do quadrante
passando por Paris, o qual é a distância entre o equador e o pólo norte.
•1795 — Barra métrica construída em latão.
•1799 — A Assembléia Nacional da França especifica a barra métrica de platina, construída em 23 de Junho de 1799
e depositada nos Arquivos Nacionais, como o padrão.
•1889 — A primeira Conferência Geral sobre Pesos e Medidas define o metro como a distância entre duas linhas
numa barra padrão de uma liga de platina com 10% de irídio, medida na temperatura de fusão do gelo.
•1927 — A sétima Conferência Geral sobre Pesos e Medidas ajusta a definição de metro como sendo a distância, a
0 °C, entre os eixos de duas linhas centrais marcadas numa barra protótipo de platina-irídio, esta barra estando
sujeita a pressão padrão de uma atmosfera e suportada por dois cilindros de pelo menos um centímetro de diâmetro,
simetricamente colocados no mesmo plano horizontal a uma distância de 571 milímetros um do outro.
•1960 — A décima primeira Conferência Geral sobre Pesos e Medidas define o metro como igual a 1.650.763,73
comprimentos de onda no vácuo da radiação correspondente à transição entre os níveis quânticos 2p10 e 5d5 do
átomo de criptônio-86.
•1983 — A décima sétima Conferência Geral sobre Pesos e Medidas define o metro como igual a distância
percorrida pela luz durante o intervalo de tempo de 1⁄299.792.458 de segundo.
•2002 — O Comitê Internacional de Pesos e Medidas recomenda que esta definição seja restrita a “distâncias, as
quais são suficientemente curtas para que os efeitos preditos pela teoria geral da relatividade sejam desprezíveis
com respeito às incertezas da medida."
1875 – [m] padrão metal Sèvres
Michleson: m = 1.553.163,5 lCd
Nobel 1907
Exercícios e Problemas
36-57P. Uma câmara selada, com 5,0 cm de comprimento e janelas
de vidro, é colocada em um dos braços de um interferômetro de
Michelson, como na Fig. 36.36. Uma luz de comprimento de onda
l = 500 nm é usada. Quando a câmara é evacuada, as franjas se
deslocam de 60 posições. A partir destes dados, determine o índice
de refração do ar a pressão atmosférica.