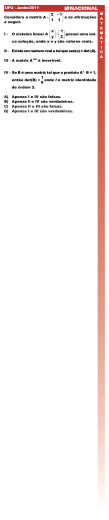Álgebra Linear Numérica 2012.1
Prova teórica - 9 de Abril de 2012
Escolher três questões para montar sua prova, respostas referente à questão
não escolhida não serão corrigidas. Todas as questões devem ser justificadas
de forma clara. Tempo: 1h50.
Nome:
Matrı́cula:
Questão
1
2
3
4
Total
Pontos
6
5
5
51/2
211/2
Correção
Prova P1
Álgebra Linear Numérica 2012.1
Nessa prova, E é um espaço vetorial de dimensão finita n sobre K.
1. A um polinômio P ∈ Kn [X], unitário de grau n, associamos
de matriz companheira de P da seguinte forma:

0 0
1 0

0 1

P = a0 + a1 X + · · · + an−1 X n−1 + X n ⇒ MP = 0 0

 .. ..
. .
0 0
1 pto
a matriz MP , chamada
0
0
0
1
..
.
···
···
···
···
...
0 ···
0
0
0
0
..
.
−a0
−a1
−a2
−a3
..
.
1 −an−1









(a) Mostre que o polinômio caracterı́stico det(X · id − MP ) de MP é P .
pto
(b) Mostre que existe um vetor v ∈ E tal que o endormorfismo representado pela matrix MP na base (e0 , . . . , en ) que seja cı́clico de ordem n (i.e. (v, MP v, . . . , MPn−1 )
é uma base de E).
1 pto
(c) Deduzir que P é o polinômio mı́nimizador de M (i.e. o polinômio unitário de
menor grau tal que P (MP ) = 0).
2 ptos
(d) * Mostre que, para um endomorfismo qualquer f ∈ L(E), se o polinômio caracterı́stico de f coincide com o polinômio minimizador de f , então existe uma
base onde a matriz de f tem a forma de uma matriz companheira. Poderá usar
a decomposição de Jordan e as propriedades de matreizes de Van der Monde.
1/
2
pto
(e) Mostre que, se λ é raı́z de P , então o vetor [1, λ, . . . , λn−1 ]T é autovetor da
matriz (MP )T . Deduzir que, se P admite n raı́zes λ0 , . . . , λn−1 em K, então
temos V · MP = V · Diag(λ0 , . . . , λn−1 ), com V sendo a matriz de Van der
Monde dos λi ’s : V = [λji ]n−1
i,j=0 .
1 pto
(f) Deduzir que se P admite n raı́zes distintas em K, então MP é diagonalizável.
Mostre um contre-exemplo caso as raı́zes não sejam distintas.
1/
2
2. Lembramos que k.k : E → R+ é uma norma em E, com K = R, se e somente se:
1. ∀(λ, v) ∈ R × E, kλ · vk = |λ| kvk.
2. ∀(v, w) ∈ E2 , kv + wk ≤ kvk + kwk.
3. ∀v ∈ E, kvk = 0R ⇒ v = 0E .
Considere L = L(E, F) o espaço vetorial das aplicações lineares de E em F, ou de
forma equivalente E = Mm×n (R) o espaço vetorial das matrizes m × n. Sejam k.kE
e k.kF umas normas sobre os espaços E e F, de dimensões respectivas n e m.
2 ptos
(a) Mostre que a aplicação k.kL : L → R, definida por kf kL = max{kf (x)kF , x ∈
E, kxkE = 1} é uma norma de L.
Consideramos agora que E = F tem uma estrutura Euclideana, com produto interno
<, >.
2 ptos
1 pto
(b) Mostre que k.k2 : L → R, que ao endomorfismo f associa a raı́z do maior autovalor de f T ◦ f é uma norma.
√
(c) Mostre que, se kvkE = kvkF = < v, v >, então k.k2 = k.kL .
Página 2 de 3.
Álgebra Linear Numérica 2012.1
Prova P1
3. Seja f ∈ L(E, F) uma aplicação linear, sendo n e m as dimensões respectivas de E e
F.
11/2 ptos
(a) Mostre
que existe umasbases de E e de F tal que a matriz de f nessas bases
idl×l
0l×k
seja
onde id é a matriz da identidade, e as dimensões k e
0(m−l)×l 0(m−l)×k
l são a precisar e a relacionar.
Consideramos agora que F tem uma estrutura Euclideana e definimos g o endomorfismo de E por g = f T ◦ f .
11/2 ptos
(b) Deduzir
queexiste uma base ortonormal BE de E na qual a matriz de g seja
Dl×l 0l×k
, onde D é uma matriz diagonal com elementos estritamente po0k×l 0k×k
sitivos1 .
2 ptos
(c) Deduzir que existe uma
√ base ortonormal
BF de F tal que a matriz de f nas
√
Dl×l
0l×k
bases BE e BF seja
, onde D é a matriz diagonal tendo,
0(m−l)×l 0(m−l)×k
na diagonal, as raı́zes dos elementos diagonais de D2 .
4. Consideramos que E tem uma estrutura euclideana com o produto interno <, >, w
um vetor unitário de E e denotamos por E0 o sub-espaço vetorial de dimensão n − 1
E0 = w⊥ e π a projeção sobre E0 . Sejam u e v dois vetores de E0 .
1/
2
(a) Mostre que a aplicação g : E0 → E0 definida por g(x0 ) = x0 + < v, x0 > ·u é
um endomorfismo. Dada as representações em coordenada de u e v numa base
ortonormal (b0 , . . . , bn−2 ), determine a representação matricial de g nessa mesma
base.
pto
11/2 ptos
(b) Sejam os endomorfismos f0 , f1 , f2 , f3 de E definidos por:
f0 (x) = π(x)+ < w, x > ·u + (< w, x > + < v, u > < w, x >) · w
f1 (x) = π(x) + (< v, π(x) > + < w, x >) · w
f2 (x) = g ◦ π(x)+ < w, x > ·u+ < w, x > ·w
f3 (x) = π(x) + (− < v, π(x) > + < w, x >) · w
Mostre que f0 = f1 ◦ f2 ◦ f3
1 pto
(c) Determine as representações matriciais desses endomorfismos na base ortonormal
(b0 , . . . , bn−2 , w), e deduzir que det(g) = 1+ < v, u >.
1 pto
(d) Seja a um automorfismo de E0 , e ga : E0 → E0 definido por ga (x0 ) = a(x0 )+ <
v, x0 > ·u. Deduzir3 que det(ga ) = det(a) (1+ < v, a−1 (u) >).
11/2 ptos
(e) Generalize o resultado anterior da seguinte forma: sejam A uma matriz quadrada
de dimensão n inversı́vel, U e V matrizes n por m, então det(A + U · V T ) =
det(I + V T A−1 U ) det(A).
1
Esses elementos são chamados de valores singulares de f .
Essa decomposição é chamada de decomposição em valores singulares - SVD.
3
Esse resultado é chamado de Lema do determinante de matrizes
2
Página 3 de 3.