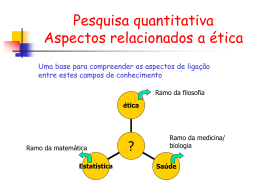
Quantificação de Fases por
Difração de Raios-x
40
Moissanite 6H
Moissanite 4H
Moissanite 3C
Moissanite 15R
Corundum
Garnet
Silicon
30
20
10
0
23.82 %
0.40 %
44.25 %
7.49 %
17.74 %
5.50 %
0.80 %
-10
-20
25
30
35
40
45
50
55
60
65
70
75
80
Determinação Qualitativa
de Fases
• Medidas relativamente rápidas => 1 hora
para medidas de rotina
• Comparação automática com banco de
dados JCPDS
• Alto grau de complexidade para amostras
com número de fases superior à 3
Análise Quantitativa de Fases
• Cada fase distinta em uma mistura possui
um coeficiente de absorção diferente
• Coeficiente de absorção também depende
da concentração das fases
• Expressão geral derivada do fator de
estrutura para uma única fase
Análise Quantitativa de Fases
• Método Externo
– Limitado a mistura de duas fases
– Dependente do tipo de amostra
– Conhecimento dos coeficientes de absorção
Análise Quantitativa de Fases
• Método por Comparação Direta
– Limitado a mistura de três fases
Análise Quantitativa de Fases
• Método do Padrão Interno
• Colocação de uma fase conhecida com
concentração conhecida
• Curva de calibração
Análise Quantitativa de Fases
• Dificuldades práticas
–
–
–
–
Superposição de picos
Orientação preferencial
Microabsorção
Extinção
Método de Rietveld
•
•
•
•
Hugo Rietveld (1964)
Difração de neutrons
Pouca disponibilidade computacional
Aplicação em difração de raios-x (1977)
Método de Rietveld
Método de Rietveld
• Processo de ajuste por mínimos quadrados
Método de Rietveld
• Programas livres
–
–
–
–
–
DBWS (1981)
GSAS (1991)
RIETAN
XRS-82
FullProof
Método de Rietveld
Ajuste Analítico de Curvas
• Uso de funções Gaussian, Lorentzian, somas de
Gaussianas ou Lorentzcianas, Voigt, pseudo-Voigt
e PearsonVII
• Descrição das simetrias e assimetrias dos picos
• Uso direto
• Grande número de variáveis, gerando os seguintes
problemas
– Correlação entre variáveis
– Perda de unicidade de solução
– Instabilidade nos cálculos de refinamento
×
-
0
E m issio n P ro file
ta n (  )
+
×
-
0
Ta rge t
+
×
-
0
S lit W idth
+
×
-
0 +
H o rizo ntia l
D ive rg en ce
2
 co t(  )
×
-
0 +
A xial
D ive rg en ce
2
S L co t(  )
-
0
C rysta llite S ize
1 / cos(2  ) C S
+
Método de Rietveld
Ajuste Analítico de Curvas
• Necessidade de uma estratégia de liberação
de variáveis
Método de Rietveld
• Qualidade de Ajuste pela avaliação dos
parâmetros:
– Rwp
– GOF (entre 1,0 e 1,3)
Método de Rietveld
• Parâmetros Fundametais
– Tese de doutorado de Alan Coelho (1997)
• Programas Livres
– X-Fit
– Koalariet
• www.ccp14.ac.uk
Método de Rietveld
Parâmetros Fundamentais
• Separação das contribuições da fonte de
emissão, do equipamento e da amostra
• Convolução destas funções
Y(2) = (W ´ G) ´ S
• Estabilidade e convergência mais robusta
• Não necessita de estratégica de ajuste
Método de Rietveld
Parâmetros Fundamentais
• Parâmetros de Emissão
– Tipo de fonte de raios-x
– Número de raias de emissão
• Parâmetros do Equipamento
– Comprimento dos braços primário e secundário
do goniômetro
– Fendas de divergência fixas e reguláveis
– Fendas soller primárias e secundárias
Método de Rietveld
Parâmetros Fundamentais
• Parâmetros do Equipamento
– Monocromador
– Perfil do ruído de fundo (Background)
Método de Rietveld
Parâmetros Fundamentais
• Parâmetros da Amostra
–
–
–
–
–
Correção do alinhamento
Deslocamento da amostra
Rugosidade superficial
Tamanho geométrico
Absorção
Método de Rietveld
Parâmetros Fundamentais
• Variáveis de Ajuste
•
•
•
•
•
•
•
Parâmetros de rede
Tamanho de cristalito
Orientação preferencial
Tensão residual
Deformação
Posições atômicas
Ocupação atômica
Método de Rietveld
Parâmetros Fundamentais
• Parâmetros Indiretos
– Densidade molecular
– Volume da célula
– Grupo espacial
1.400
Moissanite 6H
Corundum
Y2O3
Moissanite 4H
Moissanite 3C
Moissanite 15R
Quartz low
Silicon
1.200
1.000
800
600
73.26 %
9.36 %
2.69 %
5.83 %
2.25 %
4.62 %
1.05 %
0.94 %
400
200
0
-200
-400
-600
-800
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
40
Moissanite 6H
Moissanite 4H
Moissanite 3C
Moissanite 15R
Corundum
Silicon
YAG
30
20
10
0
25.65 %
4.94 %
55.74 %
2.42 %
9.92 %
1.11 %
0.22 %
-10
-20
-30
25
30
35
40
45
50
55
60
65
70
75
80
Método de Rietveld
Parâmetros Fundamentais
– Posições dos Picos
• Parâmetros de rede
• Grupos espaciais
– Intensidades dos Picos
• Estrutura cristalina
• Análise quantitativa
• Textura
Método de Rietveld
Parâmetros Fundamentais
– Largura e perfil dos Picos
• Contribuições do instrumento
• Microsestrutura (forma e tamanho dos
cristalitos, concentração de discordâncias)
– Ruído de Fundo (“Background”)
• Espalhamentos (ar, porta amostra,…)
• Ordem/desordem local
• Presença de fase amorfa
Método de Rietveld
Parâmetros Fundamentais
• Precisão na quantificação de fases
• Número máximo de fases
• Parâmetros experimentais não levados em
conta
– Umidade
– Variação do erro do ajuste em relação a
proporção das fases
– Preparação da amostra
Referências Bibliográficas
• The Rietveld Method – R. A. Young 2aEdição – Oxford Science Publications 1995
• Elements of X-Ray Diffraction – B.D.
Cullity – 2aEdição – Addison Wesley, 1978.