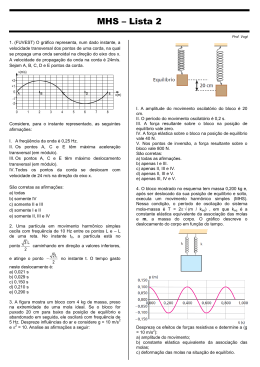
UECE 2014.1 – 2ª Fase
Para aquecer os motores vamos
dar uma pequena treinada?
Professor Vasco Vasconcelos
[email protected]
01.Dois vetores de módulos iguais são tais que o módulo da
soma deles vale (x) e , o módulo da diferença vale(y). Podese afirmar que cada um deles vale:
a) (x + y) / 2
b) (x2 + y2) /2
c) (x2 + y2) /2
d) (x2 - y2) /2
 



02. A soma dos vetores a e b é dada por S = 11 i + 2 j
e a diferença entre eles, nessa mesma ordem, é dada por





D = 5 i + 10 j . Os módulos de a e de b, medem, respectivamente:
a) 10 e 5
b) 16 e 12
c) 25 e 4
d) 8 e 6
03. Duas velas, v1 de comprimento L1=30cm e v2, de
comprimento L2 = 10 cm, são tais que a primeira v1, é
totalmente consumida em 2h e a segunda v2, em 6h.
Considerando que o consumo das velas ocorre uniformemente
no tempo e que ambas são acesas simultaneamente, determine
quanto tempo, em min, após o início da queima, as duas velas
terão um mesmo comprimento.
a) 15
b) 30
c) 60
d) 90
04. O olho humano retém durante 1/24 de segundo as
imagens que se formam na retina. Essa memória visual
permitiu a invenção do cinema. A filmadora bate 24
fotografias (fotogramas) por segundo. Uma vez revelado, o
filme é projetado à razão de 24 fotogramas por segundo.
Assim, o fotograma seguinte é projetado no exato instante em
que o fotograma anterior está desaparecendo de nossa
memória visual, o que nos dá a sensação de continuidade.
Filma-se um ventilador cujas pás estão girando no sentido
horário. O ventilador possui quatro pás simetricamente
dispostas, uma das quais pintadas de cor diferente, como
ilustra a figura. Ao projetarmos o filme, os fotogramas
aparecem na tela na seguinte sequência:
Isso nos dá a sensação de que as pás estão girando no sentido
anti-horário. Calcule quantas rotações por segundo, no
mínimo, as pás devem estar efetuando para que isto ocorra.
a) 12Hz
b) 15Hz
c) 18Hz
d) 20Hz
05. Um batalhão de infantaria sai do quartel para uma
marcha de exercícios às 5 horas da manhã, ao passo de
5km/h. Depois de uma hora e meia, uma ordenança sai do
quartel de jipe para levar um equipamento ao comandante
da marcha, ao longo da mesma estrada e a 80km/h. Quantos
minutos a ordenança levará para alcançar o batalhão?
a) 11
b) 1
c) 6
d) 3,5
06. Socorro! Socorro! Você está em dificuldades no meio
de um rio e vê duas bóias: uma na sua frente, a 3 metros
na direção da correnteza e outra a 3 metros atrás. Qual
é a melhor opção?
a)Nadar para a bóia da frente.
b) Nadar para a bóia de trás.
c) Tanto faz.
d) ficar flutuando que a de trás te pega.
07.O gordo e o magro estão nas extremidades de uma prancha
sobre rodas e resolvem trocar de posições. Não há atrito. O
que acontece com a prancha?
a) Move-se para a direita e para.
b) Move-se para a esquerda e para.
c) Move-se para a direita e continua se movendo com velocidade
constante nessa direção.
d) Move-se para a esquerda e continua se movendo com velocidade constante nessa direção.
Solução:
O centro de massa do
conjunto
(prancha
e
comediantes),
assinalado
pela linha pontilhada, não
deve se mover, pois não
existem forças externas.
Ficará, portanto, sempre um
pouco mais perto do gordo.
Logo, quando os dois trocam
posições, a prancha move-se
para a direita e pára,
mantendo o centro de massa
fixo.
Interessante e importante! Não
esqueça!
MHS - complemento
Definição de MHS
É um movimento de oscilação repetitivo,
ideal, que não sofre amortecimento, ou
seja, permanece com a mesma amplitude
ao longo do tempo.
Exemplos de MHS
Energia do MHS
Cinemática do MHS
Deslocamento em função do tempo X(t)
x(t )  A. cos(.t   )
Amplitude
Frequência
agular
Fase inicial
Instante
1
K


T
m
  2. . f
m
T  2
2
K

T
f 
Cinemática do MHS
MassaMola
Velocidade em função do tempo v(t)
v(t )  . A.sen(.t   )
Amplitude
Frequência
agular
Fase inicial
Instante
1
f 
T
  2. . f
2

T

K
m
m
T  2
K
Cinemática do MHS
MassaMola
Aceleração em função do tempo a(t)
a(t )   . A. cos(.t   )   .x(t )
2
Amplitude
2
Frequência
angular
Fase inicial
Instante
1
f 
T
  2. . f
2

T

K
m
m
T  2
K
Resumo – Cinemática do MHS
x(t )  A. cos(.t   )
v(t )  . A.sen(.t   )
a (t )   2 . A. cos(.t   )
SISTEMA MASSA MOLA
m
T  2
k
Pêndulo Simples
Período de oscilação para
pequenas amplitudes :
q
q ≤ 10°
L
T = 2..
m
L
g
e)  3 x0/7
Num sistema massa-mola, conforme a figura (superfície
horizontal sem atrito) onde k é a constante elástica da mola, a
massa é deslocada de uma distância x0, passando a oscilar. Em
que pontos a energia cinética da massa é igual a 7/9 da energia
potencial do sistema?
a)  3 x0/5
b)  2 x0/5
c)  2 x0/7
d)  3 x0/4
Vamos praticar um pouco?
Observe as quatro representações gráficas da elongação
em função do tempo, para movimentos harmônicos
simples. Em cada caso, expresse analiticamente a
elongação em função do tempo [x = f(t)].
Determine a constante elástica equivalente às seguintes
associações de molas ideais:
Duas molas iguais e um mesmo bloco participam das
duas montagens ilustradas nas figuras I e II:
Qual a diferença entre elas?
Muito cuidado!
A mola helicoidal (figura 1), de constante elástica k=12N/m,
foi partida em 3 partes iguais. Em seguida, essas 3 partes
foram associadas em paralelo (figura 2) e em série (figura 3).
As massas das figuras 2 e 3 são iguais e valem 100g. Adote
g=10m/s2 e determine:
a) a constante elástica de cada parte.
b) o período de oscilação do conjunto quando as três molas
estão associadas em paralelo.
c) o período de oscilação do conjunto quando as três molas
estão associadas em série.
Um pêndulo simples é preso ao teto de um elevador, conforme mostra a figura.
Muito importante!
Observe as seguintes situações:
I. O elevador permanece em repouso ou move-se verticalmente
com velocidade constante.
II. O elevador acelera para cima.
III. O elevador acelera para baixo.
Pode-se afirmar que:
a) o período do pêndulo em II é maior do que em I
b) o período do pêndulo III é maior do que em I
c) a frequência do movimento oscilatório em II é menor do que
em III
d) somente em I o pêndulo pode oscilar
"Destino é uma desculpa tola para o
fracasso."
Ambrose Bierce *
*Ambrose Gwinnett Bierce foi um crítico satírico, escritor e jornalista estadunidense,
particularmente conhecido pela sua obra O Dicionário do Diabo.