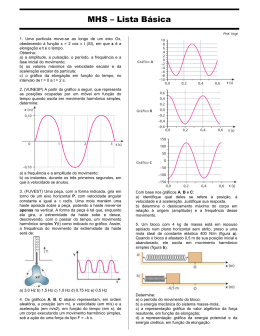
MHS – Lista 2
Prof. Vogt
1. (FUVEST) O gráfico representa, num dado instante, a
velocidade transversal dos pontos de uma corda, na qual
se propaga uma onda senoidal na direção do eixo dos x.
A velocidade de propagação da onda na corda é 24m/s.
Sejam A, B, C, D e E pontos da corda.
v(m/s)
+2
+1
0 A
-1
-2
B
0
1
2
C
3
4
D
5
6
E
7
x(m)
8
Considere, para o instante representado, as seguintes
afirmações:
I. A freqüência da onda é 0,25 Hz.
II. Os pontos A, C e E têm máxima aceleração
transversal (em módulo).
III. Os pontos A, C e E têm máximo deslocamento
transversal (em módulo).
IV. Todos os pontos da corda se deslocam com
velocidade de 24 m/s na direção do eixo x.
São corretas as afirmações:
a) todas
b) somente IV
c) somente II e III
d) somente I e II
e) somente II, III e IV
2. Uma partícula em movimento harmônico simples
oscila com frequência de 10 Hz entre os pontos L e – L
de uma reta. No instante t0, a partícula está no
ponto
3L
2
I. A amplitude do movimento oscilatório do bloco é 20
cm.
II. O período do movimento oscilatório é 0,2 s.
III. A força resultante sobre o bloco na posição de
equilíbrio vale zero.
IV. A força elástica sobre o bloco na posição de equilíbrio
vale 40 N.
V. Nos pontos de inversão, a força resultante sobre o
bloco vale 800 N.
São corretas:
a) todas as afirmações.
b) apenas I e III.
c) apenas II, III e IV.
d) apenas II, III e V.
e) apenas III, IV e V.
4. O bloco mostrado no esquema tem massa 0,200 kg e,
após ser deslocado da sua posição de equilíbrio e solto,
executa um movimento harmônico simples (MHS).
Nessa condição, o período de oscilação do sistema
mola-massa é T = 2√m / keq) , em que keq é a
constante elástica equivalente da associação das molas
e m, a massa do corpo. O gráfico descreve o
deslocamento do corpo em função do tempo.
caminhando em direção a valores inferiores,
2L
no instante t. O tempo gasto
2
neste deslocamento é:
a) 0,021 s
b) 0,029 s
c) 0,150 s
d) 0,210 s
e) 0,290 s
e atinge o ponto 
3. A figura mostra um bloco com 4 kg de massa, preso
na extremidade de uma mola ideal. Se o bloco for
puxado 20 cm para baixo da posição de equilíbrio e
abandonado em seguida, ele oscilará com frequência de
2
5 Hz. Despreze influências do ar e considere g = 10 m/s
2
e  = 10. Analise as afirmações a seguir:
Despreze os efeitos de forças resistivas e determine a (g
2
= 10 m/s ):
a) amplitude do movimento;
b) constante elástica equivalente da associação das
molas;
c) deformação das molas na situação de equilíbrio.
0
5. Um bloco suspenso por uma mola oscila verticalmente
em movimento harmônico simples, como representa a f
igura 1. No instante t = 0, ele está passando pela sua
posição de equilíbrio (y = 0). A velocidade escalar v
desse bloco varia com o tempo t, conforme o gráfico
apresentado na figura 2.
9. O período de um relógio tem período T 0 a 20 C. Esse
0
relógio é levado a um local onde a temperatura é 40 C.
Sabendo que o material que constitui o pêndulo tem
coeficiente de dilatação linear α, pode-se afirmar que o
novo período desse pêndulo vale:
a) T0 (1  20)
T0
1  20
c) 2T0 5
b)
d)
T0
(1  20)1 2
e) T0 (1  20)1 2
10. Considere que a maré em um porto oscile em
movimento harmônico simples. Num certo dia, sabe-se
que a profundidade máxima será de 12m às 12h30min e
a profundidade mínima será de 8,0m às 18h30min.
a) O período de oscilação das ondas.
b) A pulsação de oscilação das ondas.
c) Calcule o intervalo de horário, antes do por do Sol,
em que um navio de 8,5m de calado poderá entrar neste
porto, com uma margem de segurança mínima de 0,50m
de água entre o fundo do navio e o fundo do mar.
a) Determine a função horária da elongação, y = f(t),
desse movimento.
b) Considerando  = 3, quanto vale a “área” destacada
na figura 2?
Respostas
6. A figura representa um pêndulo simples, de período
igual a T. Colocando-se um prego (P) na posição
indicada, o pêndulo, na máxima elongação para a
esquerda, fica com a configuração indicada pela linha
pontilhada, voltando depois à sua configuração inicial.
Qual é o período de oscilação desse sistema?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
7. Um corpo de massa m, preso a uma mola de
constante elástica K, executa um movimento harmônico
simples ao longo de um eixo horizontal Ox. As
elongações do corpo variam de x = – A até x = A.
Determine a elongação quando a energia cinética do
bloco iguala-se à energia potencial elástica, indicando o
resultado num gráfico dessas energias em função da
posição.
8. Um pequeno objeto executa MHS com período de 8s
entre os pontos R e –R de uma reta. No instante inicial t0
o referido objeto encontra-se no ponto R/2 deslocandose em direção a valores inferiores e chega ao ponto –R
no instante t. Pede-se:
a) O deslocamento angular efetuado.
b) O tempo gasto neste deslocamento.
2
C
B
A
a) 0,1 m; b) 50 N/m; c) 0,04 m.
a) y = (3 / 2 cos [2 . t / 3 +  / 2] b) 0,5 m
3T / 4
x = ± A√2
a) 135º b) 3s
E
a) 12h b) /6 rad/s c) das 8h30min até às 16h30min