Probabilidade II
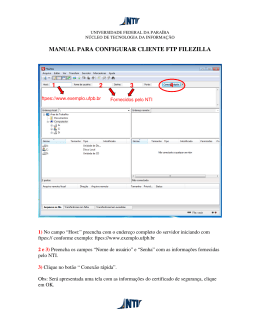
Departamento de Estatística
Universidade Federal da Paraíba
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
1/1
Variáveis Bidimensionais
Até o momento, consideramos apenas o caso de variáveis aleatórias
unidimensionais.
Em muitas situações, no entanto, estamos interessados em observar duas ou
mais características simultaneamente.
É muito comum estarmos interessados no comportamento conjunto de várias
variáveis.
Inicialmente vamos tratar de duas variáveis.
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
2/1
Variáveis Bidimensionais
Estudar peso e altura de um grupo de pessoas.
Avaliar a relação entre a nota do vestibular e o número de reprovações em
alunos do curso de estatística.
Estudar o tamanho do tumor e o tipo de tratamento em pacientes com
Câncer.
Um dado é lançado e simultaneamente é girada a roda de uma roleta.
Estamos interessado no resultado do lançamento do dado e no número
observado na roleta.
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
3/1
Variáveis Bidimensionais
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
4/1
Variáveis Bidimensionais
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
5/1
Normal Bivariada
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
6/1
Variáveis Bidimensionais Discretas
Definição 10.1 (X , Y ) será uma variável discreta bidimensional se os valores
possíveis de (X , Y ) forem finitos ou infinitos enumeráveis.
Isto é, os valores possíveis de (X , Y ) possam ser representados por (xi , yj ),
i = 1, 2, . . . , n, . . .; j = 1, 2, . . . , m, . . ..
Definição 10.2 (Função de probabilidade conjunta) Seja (X , Y ) uma variável
aleatória discreta bidimensional. A cada resultado possível (xi , yj ) associaremos
um número p(xi , yj ) representando P (X = xi , Y = yj ) e satisfazendo ás seguintes
condições:
i) p(xi , yj ≥ 0)
ii)
P∞ P ∞
j =1
i =1
p(xi , yj ) = 1
Definição 10.3 A distribuição de probabilidade da variável aleatória (X , Y ) é uma
tabela que associa a cada valor dessa variável sua correspondente probabilidade.
Ela é denominada também distribuição conjunta de X , Y .
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
7/1
Variáveis Bidimensionais Discretas
Exemplo 1 Foi perguntado aos alunos de Probabilidade II se eles estão em um
relacionamento sério (namoro, casamento,...), variável representada por X , e a
religião, variável representada por Y . Construa a distribuição de probabilidade
conjunta de (X , Y ).
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
8/1
Variáveis Bidimensionais Discretas
Exemplo 1
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
9/1
Variáveis Bidimensionais Discretas
Podemos associar a cada variável aleatória bidimensional (X , Y ) duas variáveis
aleatórias unidimensionais, X e Y individualmente.
Isto é, podemos estar interessados na distribuição de probabilidade de X e/ou Y
separadamente.
A distribuição de probabilidade de X , denominada distribuição de probabilidade
marginal de X é obtida calculando-se:
p(xi ) = P (X = xi ) =
∞
X
P (X = xi , Y = yj )
j =1
A distribuição de probabilidade de Y , denominada distribuição de probabilidade
marginal de Y é obtida calculando-se:
p ( yi ) = P ( Y = yj ) =
∞
X
P ( X = xi , Y = yj )
i =1
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
10 / 1
Variáveis Bidimensionais Discretas
Exemplo 2 Obtenha as distribuições marginais de X e Y para o Exemplo 1.
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
11 / 1
Variáveis Bidimensionais Discretas
Exemplo 2
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
12 / 1
Variáveis Bidimensionais Discretas
Exemplo 3: Uma empresa atende encomendas de supermercados dividindo os
pedidos em duas partes de modo a serem atendidos, de forma independente,
pelas suas duas fábricas. Pode haver atraso no cronograma de entrega da
fábrica I com probabilidade 0.1 e na fábrica II com probabilidade 0.2. Suponha
que para um certo pedido, a indústria recebe R $200, 00 pela encomenda total
entregue, mas paga uma multa de R $20, 00 para cada fábrica que atrasar sua
parte. Considere que o supermercado que fez a encomenda, criou um índice
relacionado à pontualidade da entrega. Este índice, atribui 10 pontos para cada
parte da encomenda entregue dentro do cronograma previsto. Vamos denotar por
X o valor recebido pelo pedido e Y o índice obtido. Encontre a distribuição
conjunta de (X , Y ) e as distribuições marginais.
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
13 / 1
Variáveis Bidimensionais Discretas
Exemplo 3
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
14 / 1
Variáveis Bidimensionais Discretas
Exemplo 3
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
15 / 1
Variáveis Bidimensionais Contínuas
Definição 10.4 (X , Y ) será uma variável contínua bidimensional se (X , Y ) puder
tomar todos os valores em algum conjunto não-enumerável do plano euclidiano.
Por exemplo, se (X , Y ) puder tomar todos os valores no retângulo
{ (x , y )| a ≤ x ≤ b , c ≤ y ≤ d } .
Definição 10.5 (Função densidade de probabilidade conjunta) Seja (X , Y ) uma
variável aleatória contínua bidimensional tomando todos os valores em alguma
região R do plano euclidiano. A função densidade de probabilidade conjunta f é
uma função que satisfaz às seguintes condições:
i) f (x , y ) ≥ 0
ii)
RR
R
f (x , y )dxdy = 1
Dessa forma, P (a < X < b, c < Y < d ) =
Prof. Tarciana Liberal (UFPB)
RbRd
a
c
f (x , y )dxdy .
Aula Variáveis Aleatórias Bidimensionais
11/13
16 / 1
Variáveis Bidimensionais Contínuas
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
17 / 1
Variáveis Bidimensionais Contínuas
Exemplo 4 Seja (X , Y ) uma variável aleatória bidimensional cuja densidade de
probabilidade é dada por: f (x , y ) = c (x 2 + xy ) para 0 ≤ x ≤ 2 e 0 ≤ y ≤ 4 sendo
zero no complementar desse retângulo. Calcule a probabilidade P (X + Y ≤ 3)
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
18 / 1
Variáveis Bidimensionais Contínuas
Exemplo 4
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
19 / 1
Variáveis Bidimensionais Contínuas
Dada a densidade conjunta das variáveis X e Y , podemos determinar as
densidades de X e Y separadamente.
Essas densidades são denominadas densidades marginais de X e de Y e
denotadas por fX (x ) e fY (y ).
∞
Z
f (x , y )dy
fX (x ) =
−∞
Z
∞
fY (y ) =
f (x , y )dx
−∞
Quando não houver menção explícita ao conjunto de valores ondef (x , y ) > 0,
suporemos que esse conjunto é o plano
(R 2 = {(x , y ) : −∞ < x < ∞, −∞ < y < ∞}).
Note que fX (x ) e fY (y ) são de fato densidades deRprobabilidade,
pois são
R
não-negativas e sua integral na reta é igual a um (
f (x , y )dxdy = 1).
R
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
20 / 1
Variáveis Bidimensionais Contínuas
Exemplo 5 Seja (X , Y ) uma par de variáveis aleatórias cuja densidade conjunta
é dada por: f (x , y ) = 8xy para 0 < x < y < 1 sendo zero no complementar.
Determine as densidades marginais de probabilidade de X e de Y e calcule a
probabilidade P (0 < X < 0.5, 0 < Y < 0.5).
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
21 / 1
Variáveis Bidimensionais Contínuas
Exemplo 5
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
22 / 1
Exemplo 6
Dois característicos do desempenho do motor de um foguete são X e Y . Suponha
que (X , Y ) seja uma variável aleatória contínua bidimensional com fdp conjunta:
f (x , y ) = 2(x + y − 2xy ) para 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 sendo zero no complementar.
Determine as densidades marginais de probabilidade de X e de Y .
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
23 / 1
Variáveis Bidimensionais Contínuas
Exemplo 6
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
24 / 1
Função de distribuição acumulada
Definição 10.6 A função de distribuição de uma variável aleatória bidimensional
(X , Y ) é dada por:
F (x , y ) = P (X ≤ x , Y ≤ y ),
−∞ < x < ∞ e
−∞<y <∞
Para o caso discreto:
F (x , y ) = P (X ≤ x , Y ≤ y ) =
X X
P ( X = xi , Y = yj )
i :xi ≤x j :yj ≤y
Para o caso contínuo:
Z
x
y
Z
F (x , y ) = P (X ≤ x , Y ≤ y ) =
f (u , v )dudv
−∞
−∞
Se F é a função de distribuição de uma V.A. bidimensional com f.d.p f , então
f (x , y ) =
∂ 2 F (x ,y )
.
∂ x∂ y
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
25 / 1
Função de distribuição acumulada
Para o caso discreto:
P (X ≤ x ) =
x X
∞
X
P (X = xi , Y = yj )
i =1 j =1
P (Y ≤ y ) =
y
∞ X
X
P (X = xi , Y = yj )
i =1 j =1
Para o caso contínuo:
x
Z
∞
Z
P (X ≤ x ) =
f (u , v )dudv
−∞
.
Z
∞
−∞
Z
y
P (Y ≤ y ) =
f (u , v )dudv
−∞
.
Prof. Tarciana Liberal (UFPB)
−∞
Aula Variáveis Aleatórias Bidimensionais
11/13
26 / 1
Função de distribuição acumulada
Propriedades:
i) limx →−∞,y →−∞ F (x , y ) = 0 e limx →∞,y →∞ F (x , y ) = 1
ii) F (x , y ) é contínua à direita em cada uma das variáveis x e y .
iii) F (x , y ) é não-decrescente em cada uma das variáveis.
Estas propriedades são extensões naturais para o caso bidimensional das
propriedades da função de distribuição de uma variável aleatória unidimensional
X.
O intervalo (−∞, x ] é substituído pelo retângulo (−∞, x ] × (−∞, y ].
Quando fazemos x → −∞, este retângulo tende ao conjunto vazio no plano e sua
imagem inversa tende ao conjunto vazio no espaço amostral que tem
probabilidade zero.
Quando x → ∞ e y → ∞, o retângulo em questão tende para o plano todo, cuja
imagem inversa é o espaço amostral que tem probabilidade 1.
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
27 / 1
Função de distribuição acumulada
Para uma variável aleatória unidimensional X verificamos que:
P (a < X ≤ b) = F (b) − F (a).
No caso bidimensional vimos que o análogo a um intervalo da forma (a, b] é um
retângulo da forma {(x , y ) : a1 < x ≤ b1 , a2 < y ≤ b2 }.
A probabilidade dos valores de X e de Y pertencerem a esse retângulo é dada
por:
P (a1 < X ≤ b1 , a2 < Y ≤ b2 ) = F (b1 , b2 ) − F (a1 , b2 ) − F (a2 , b1 ) + F (a1 , a2 )
DEMONSTRAÇÃO
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
28 / 1
Exemplo 7
Determine a função de distribuição da variável aleatória do exemplo 4.
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
29 / 1
Variáveis Bidimensionais Contínuas
Exemplo 7
Prof. Tarciana Liberal (UFPB)
Aula Variáveis Aleatórias Bidimensionais
11/13
30 / 1