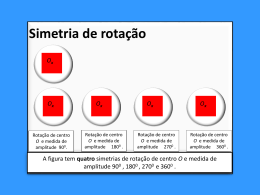
Programa de Formação Contínua em
Matemática para Professores do 2º Ciclo
Escola Básica do 2º e 3º Ciclos Professor Gonçalo Sampaio
Rosáceas
“A geometria, presente nas civilizações mais primitivas, constitui-se num
importante instrumento de leitura, conhecimento e domínio da natureza.
Esta, em suas infinitas estruturas, serve como fonte de inspiração para as
criações que expressam as representações imaginárias das distintas
culturas. Um bom exemplo dessa relação são os desenhos das “mandalas”,
encontradas nas mais antigas inscrições e grafismos da humanidade.”
(Roberto Alcarria do Nascimento, Maria Antonia Benutti,
Aniceh Farah Neves, 2007)
Construções com areia colorida
Navajo
Tibete
Yin Yang
“Enquanto uso sagrado aparece na construção de templos, que adornam
catedrais. A denominação “rosácea”, forma circular com elementos
internos que lembram rosas, deve-se a uma não aceitação dos elementos
pagãos pelo cristianismo.”
(Roberto Alcarria do Nascimento, Maria Antonia Benutti,
Aniceh Farah Neves, 2007)
“rosáceas”, propriedades:
• nâo têm translações nem reflexões deslizantes;
• têm apenas um ponto fixo;
• grupo de simetria finito;
• algumas têm apenas rotações;
• não há nenhuma que só tenha reflexões;
• C n ou D n sempre!?
Tipos de rosáceas


Cn (cíclicas)

A sua construção obtémse apenas pela rotação
do elemento base.

Dn (diedral)
A sua construção obtémse pela rotação e pela
reflexão em relação a um
eixo.
Com n finito
n=
1
2
3
4
5
6
n=
1
2
3
4
5
6
Rosáceas Diedrais
Considera agora apenas as rosáceas do tipo D (diedrais). Como as
podemos caracterizar relativamente ao seu grupo de simetria?
Observa a imagem abaixo. Repara que ela tem três eixos de simetria
(abaixo assinalados).
Observa agora a seguinte rosácea:
Rodando o disco anterior e colocando o ponto vermelho em cada uma das
3 posições indicadas abaixo, é possível sobrepor a imagem de cima à de
baixo. Esta rosácea tem 3 simetrias de rotação.
Repara que o número de simetrias de reflexão é sempre igual ao número de
simetrias de rotação. Isso não é coincidência! Uma rosácea com n simetrias de
reflexão tem exactamente n simetrias de rotação! Tal rosácea é representada
por Dn.
C2
D3
C6
D4
C8
D8
Bibliografia
MANDALAS E ROSÁCEAS: EM BUSCA DE NOVAS ABORDAGENS PARA ANTIGOS
CONTEÚDOS
Roberto Alcarria do Nascimento; Maria Antonia Benutti; Aniceh Farah Neves
UNESP - Universidade Estadual Paulista “Júlio de Mesquita Filho”, Departamento de
Artes e Representação Gráfica, 2007.
http://www.mandalaproject.org/What/Index.html
http://www.matematita.it
Veloso; Universidade Lusófona Complementos de Geometria 2003-2004
Programas informáticos:
Kali (freeware)
Tess (shareware)
FIM
Trabalho realizado pelo grupo de Formação Contínua de
Matemática - 2º Ciclo – E.B.2/3 Prof. Gonçalo Sampaio
Ano lectivo 2008-2009