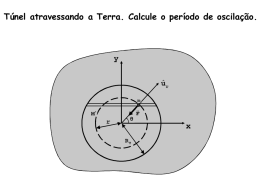
MHS 01) UNITAU- Uma partícula oscila ao longo do eixo x com movimento harmônico simples, dado 3 por x=3,0cos( t + ), onde x é dado em cm e 2 2 t em segundos. Nessas condições, pode-se afirmar que a amplitude, a freqüência e a fase inicial valem, respectivamente: a) 3,0cm, 4Hz, (3π/2)rad b) 1,5cm, 4Hz, (3π/2)rad c) 1,5cm, 4Hz, 270° d) 3,0cm, 0,5Hz, (3π/2)rad e) 3,0cm, 0,25Hz, (3π/2)rad 02) UFV- Uma partícula presa a uma mola executa um movimento harmônico simples. É CORRETO afirmar que o módulo da velocidade da partícula é: a) máximo quando a elongação é máxima. b) mantido constante. c) máximo quando ela apresenta a aceleração máxima. d) mínimo quando a elongação é mínima. e) mínimo quando ela apresenta a aceleração máxima. 03) MACKENZIE- Um corpo de 100g, preso a uma mola ideal de constante elástica 2.103 N/m, descreve um MHS de amplitude 20cm, como mostra a figura. A velocidade do corpo quando sua energia cinética é igual à potencial, é: a) 20 m/s b) 16 m/s c) 14 m/s d) 10 m/s e) 5 m/s 04) MACKENZIE- Um corpo C, de massa 1,00.10-1 kg, está preso a uma mola helicoidal de massa desprezível e que obedece à Lei de Hooke. Num determinado instante, o conjunto se encontra em repouso, conforme ilustra a figura 1, quando então é abandonado e, sem atrito, o corpo passa a oscilar periodicamente em torno do ponto O. No mesmo intervalo de tempo em que esse corpo vai de A até B, o pêndulo simples ilustrado na figura 2 realiza uma oscilação completa. Sendo g = 10 m/s2, a constante elástica da mola é: a) 0,25 N/m b) 0,50 N/m c) 1,0 N/m d) 2,0 N/m e) 4,0 N/m 05)UFC- Uma partícula, de massa m, movendose num planohorizontal, sem atrito, épresa a um sistema de molasde quatro maneiras distintas, mostradas a seguir. Com relação às freqüências de oscilação da partícula,assinale a alternativa correta. a) As freqüências nos casos II e IV são iguais. b) As freqüências nos casos III e IV são iguais. c) A maior freqüência acontece no caso II. d) A maior freqüência acontece no caso I. e) A menor freqüência acontece no caso IV 06) UFPR-A figura abaixo mostra um gráfico da força aplicada sobre uma mola em função da deformação apresentada por ela. Com base nesse gráfico, a constante elástica da mola é: a) 5,0 × 10-3 N/m. b) 2,0 × 102 N/m. c) 32 N/m. d) 8,0 × 10-2 N/m. e) 8,0 N/m. a) M.R.U.(movimento retilíneo uniforme). b) M.R.U.A.(movimento retilíneo uniformementeacelerado). c) M.R.U.R.(movimento retilíneo uniformementeretardado). d) M.C.U.V. (movimento circular uniformentevariado). e) M.H.S. (movimento harmônico simples). 08) UEM-A função horária da posição de uma partícula querealiza um Movimento Harmônico Simples (MHS) éx= A.cos (ωt+ φ0) . Sabe-se que: • xrepresenta a posição assumida pela partícula em função do tempo t, a partir de t0= 0 ; • Arepresenta a amplitude do movimento; •φ0representa a fase inicial do movimento; • ω representa a freqüência angular do movimento. A figura a seguir apresenta o gráfico da funçãohorária da posição de uma partícula que descreveum MHS segundo um certo referencial. 07) MACKENZIE- Uma partícula descreve um movimento circular uniformesobre uma mesa horizontal, conforme a figuraa seguir. O movimento exibido pela projeção ortogonal das posiçõesassumidas pela partícula, num anteparo dispostoperpendicularmente à mesma, é um: A função horária da posição dessa partícula com dados no Sistema Internacional (SI) de unidades é a) x = 0,10 cos( t + )m. 2 2 b) x = 0,20 cos( t + )m. 2 2 3 c) x= 0,10 sen( t + )m. 2 2 d) x= 0,20 cos( t)m. 2 3 e)x= 0,10 cos( t + )m. 2 2 09) ACAFE- O gráfico apresentado mostra a elongação em função do tempo para um movimento harmônico simples. A alternativa que contém a equação horária correspondente,no SI, é: Gabarito: d 10) MACKENZIE- Um corpo de 50g, preso à extremidade de uma mola ideal (constante elástica=3,2N/m) comprimida de 30cm, é abandonado do repouso da posição A da figura. A partir desse instante, o corpo inicia um movimento harmônico simples. Despreze os atritos e adote o eixo x com origem no ponto de equilíbrio do corpo (ponto O) e sentido para a direita. A função que mostra a velocidade desse corpo em função do tempo, no Sistema Internacional, é: a)v = -2,4 sen (8.t + π) b) v = -0,3 sen (3,2.t + π/2) c) v = -7,2 sen (4.π.t + π) d) v = -2,7 sen (4.t + π) e) v = -1,2 sen (2.t + π/4) 11) UFG- Uma mola de constante elástica k = 50 N/m e massa desprezível tem uma extremidade fixa no teto e a outra presa a um corpo de massa m=0,2kg. O corpo é mantido inicialmente numa posição em que a mola está relaxada e na vertical. Ao ser abandonado, ele passa a realizar um movimento harmônico simples, em que a amplitude e a energia cinética máxima são, respectivamente:Dado: g = 10 m/s2 a)4 cm e 0,04 J b) 4 cm e 0,08 J c) 8 cm e 0,04 J d) 8 cm e 0,08 J e) 8 cm e 0,16 J 12) UEM- Duas molas idênticas de constante elástica K sãoconectadas em paralelo (figura 1) e em série (figura 2) a um bloco de massa M. Qual a razão entre o período de oscilação das molas conectadas em paralelo e o período de oscilação das molasconectadas em série? a) 2 b) 4 c) 1/2 d) 1 e) 3/4 13) PUCPR- Uma partícula move-se em MHS numa trajetória retilínea. A figura mostra a energia potencial da partícula em função de sua coordenada X. A energia total da partícula é constante e vale 20 Joules. Considere as afirmações: 15) UFSM- Uma partícula de massa m, presa a uma mola, executaum Movimento Harmônico Simples (MHS) com operíodo de 16 s. Uma partícula de massa 4 m, presaà mesma mola, executará um MHS com o período(em s) de: a) 4 b) 8 c) 16 d) 32 e) 64 16) UEL- A partícula de massa m, presa à extremidade deuma mola, oscila num plano horizontal de atrito desprezível,em trajetória retilínea em torno do ponto deequilíbrio, O. O movimento é harmônico simples, deamplitude x. I - Na posição X0 a energia cinética da partícula é máxima. II - Entre as posições X1 e X2 a energia cinética é constante. III - Nas posições X1 e X2 a energia cinética da partícula é nula. IV - Na posição X0 a energia cinética da partícula é nula. a) Somente I é correta. b) Somente II é correta. c) I e III são corretas. d) III e IV são corretas. e) II e IV são corretas. 14) UTFPR- O período do Movimento Harmônico Simples (MHS) de um sistema massa-mola: a)depende da massa do ponto material em movimento. b) depende da amplitude de oscilação. c) independe da massa do ponto material. d) independe da constante elástica. e) independe da freqüência de oscilação. Considere as afirmações: I. O período do movimento independe de m. II. A energia mecânica do sistema, em qualquer pontoda trajetória, é constante. III. A energia cinética é máxima no ponto O. É correto afirmar que somente: a) I é correta. b) II é correta. c) III é correta. d) I e II são corretas. e) II e III são corretas. 17) UFPR-Com relação a um pêndulo simples, constituído por uma pequena esfera de metal de massa m, suspensa por um fio inextensível de comprimento L e que oscila com pequena amplitude, considere as seguintes afirmativas: I.O período desse pêndulo depende da massa da esfera. II. A freqüência aumentará se o comprimento do fio for aumentado. III. Se o pêndulo completar 100 oscilações em 50 s, sua freqüência será 2 Hz. IV. Medindo-se o período de oscilação do pêndulo, é possível determinar a aceleração da gravidade local. Assinale a alternativa correta. a)Somente as afirmativas III e IV são verdadeiras. b) Somente a afirmativa I é verdadeira. c) Somente a afirmativa II é verdadeira. d) Somente as afirmativas I e III são verdadeiras. e) Somente as afirmativas II e IV são verdadeiras. 18) UEM- O peso de um objeto na Lua é 1/6 de seu peso na Terra. Um relógio de pêndulo que oscila com umperíodo de 1s na Terra oscilará, sobre a Lua, comum período de: a) (1/ 6 ) s. b) 1,6 s. c) 6,0 s. d) 1,0 s. e) 6 s. 19) UTFPR-Um relógio de pêndulo é construído com umfino fio de aço de 70 cm de comprimento e massapendular 100 g. O pêndulo do relógio é posto a scilar com período de 2s num local onde aemperatura é de 20ºC.arque a afirmativa INCORRETA. a) Durante o verão (θ = 35ºC) ou o inverno (θ = 5ºC) haverá uma alteração no período deoscilação. b) Se este relógio for levado para um local comvalores de latitude e altitude diferentes da inicial, registraremos alteração no período deoscilação. c) Se a massa pendular for aumentada ou reduzida em 10 g, não observaremos alteração no valor do período de oscilação. d) Se variarmos a amplitude de oscilação em pequenos valores, de forma que o ângulo de abertura em relação à posição de equilíbrionão ultrapasse 10º, não observaremos variaçãono período de oscilação. e)Se o comprimento do fio for reduzido em 5% do seu valor inicial, não registraremos alteração no período de oscilação 20) UTFPR-Dado um pêndulo formado por um fio de comprimento L = 1m, com massa desprezível, ao qual é ligada uma pequena esfera de massa m = 1Kg. Uma extremidade do pêndulo é presa ao teto de modo que a massa presa à outra extremidade possa oscilar sujeita à atração gravitacional. Dispõe-se de um relógio para efetuar medidas do período de oscilação, T. Nota-se que, para ângulos pequenos em relação à posição de equilíbrio, T=T0, com T0 constante. É correto afirmar que: a) o pêndulo realiza um movimento harmônico e, para L=1m; se a massa original for substituída por outra de 4Kg, o período será alterado para T = 4T0. b) o pêndulo realiza um movimento periódico e, para L=1m; se a massa original for substituída por outra de 16Kg, o período será alterado para T = 4T0. c) o período de oscilação do pêndulo depende do módulo da aceleração da gravidade local, g, sendo diretamente proporcional a g. d) o pêndulo realiza um movimento harmônico e, para m=1Kg; se o comprimento do fio for alterado para L=2m, o período será alterado para T = 2T0. e)o pêndulo realiza um movimento periódico e, para m=1Kg; se o comprimento do fio for alterado para L=4m, a freqüência de oscilação 1 será modificada para . 2T0 21) UFRS- A figura a seguir representa seis pêndulos simples, que estão oscilando num mesmo local. O pêndulo P executa uma oscilação completa em 2 s. Qual dos outros pêndulos executa uma oscilação completa em 1 s? a) I. b) II. c) III. d) IV. e) V. 22) UEM- Tomando-se como base a conservação da energiamecânica, assinale o que for correto. 01. Em qualquer circunstância, a energia mecânicade uma partícula é constante. 02. A energia potencial não pode ser transformadaem energia cinética. 04. Não é possível determinar a energia potencial deuma partícula quando a sua energia cinética énula. 08.Durante a queda de um corpo no vácuo, aenergia mecânica do corpo permanececonstante. 16.A energia mecânica de uma partícula emmovimento harmônico simples (MHS) éproporcional ao quadrado da amplitude domovimento. 32.Joga-se uma pedra verticalmente para cima. Aenergia cinética da pedra é máxima no momentoem que ela sai da mão. 64. Em qualquer circunstância, o tempo empregadopor uma partícula para se deslocar de umaposição para outra pode ser determinadodiretamente a partir da expressão que caracterizaa conservação da energia mecânica. Gabarito: 56 23) UEM-Suponha que um pequeno corpo, de massa m, estejapreso na extremidade de um fio de peso desprezível,cujo comprimento é L, oscilando com pequenaamplitude, em um plano vertical, como mostra afigura a seguir. Esse dispositivo constitui umpêndulo simples que executa um movimentoharmônico simples. Verifica-se que o corpo, saindode B, desloca-se até B' e retorna a B, 20 vezes em 10s. Assinale o que for correto. 02.A frequência de oscilação do pêndulo é 0,5 Hz. 04.Se o comprimento do fio L for 4 vezes maior, operíodo do pêndulo será dobrado. 08. Se a massa do corpo suspenso for triplicada, suafreqüência ficará multiplicada por 3 . 16. Se o valor local de g for 4 vezes maior, afreqüência do pêndulo será duas vezes menor. 32.Se a amplitude do pêndulo for reduzida àmetade, seu período não modificará. Gabarito: 36 24) UEM - Considere um ponto material de massa m que oscila emtorno de uma posição de equilíbrio, em trajetóriaretilínea, livre de forças dissipativas. Assinale a(s)alternativa(s) correta(s). 01.A função x = f (t) , na qual x é o deslocamento doponto material e t é o tempo, é bem representada pelográfico abaixo. 02. O gráfico abaixo representa a velocidade v do pontomaterial em função do tempo t. 04. A força restauradora que atua sobre o ponto materialé inversamente proporcional à amplitude domovimento. 08.O gráfico do período T de oscilação em função damassa m do ponto material é bem representado pelográfico abaixo. 01. O período deste pêndulo é 2,0 s. 16.A força restauradora, que atua sobre o ponto material,em relação ao deslocamento do mesmo, érepresentada por uma função linear. Gabarito: 25 25) UEM -Considere uma onda mecânica que se propaga em uma corda homogênea de acordo com a função horária y = 2cos2π(2t - 4x) , para x e y dados em centímetros e t dado em segundos, e assinale o que for correto. 01.A amplitude da onda é 2 cm. 02. O comprimento de onda da onda é 4 cm. 04.O período de oscilação da onda é 0,5 s. 08. A velocidade de propagação da onda no meio é2 cm/s. 16.A onda que se propaga na corda é progressiva. Gabarito: 21 26) UEM - Um corpo de massa M é mantido em repouso, na posição i indicada na figura abaixo, por meio de duas linhas inextensíveis e de massa desprezível, 1 e 2. Corta-se a linha 2 e a massa inicia uma oscilação pendular. Despreze a resistência do ar e assinale o que for correto. 01.Quando o corpo está na posição A ou na posição C, o módulo da tração na linha 1 é o mesmo. 02. Quando o corpo está na posição B, a tração na linha 1é igual ao seu próprio peso. 04. O espaço percorrido pelo corpo de massa M pode sercalculado por meio da equação S(t) = at2/2 (a é omódulo da aceleração resultante do corpo e t é otempo). 08.Quando o corpo está na posição B, sua aceleraçãocentrípeta é máxima. 16.Quando o corpo está na posição A ou na posição C, omódulo de sua velocidade é o mesmo. Gabarito: 25 27) UEM - Considerando a função posição 𝜋 𝑥 𝑡 = 2 cos(0,4 𝜋 𝑡 + 6 ), com x dado em centímetros e t em segundos, de um corpoem movimento harmônico simples, assinale o que forcorreto. 01.Nas mesmas unidades acima, podemos tambémexpressar x(t) na forma 3 cos (0,4 π t) − sen (0,4 π t), em que t ≥ 0 . 2 02. O período do movimento é segundos. 𝜋 04)O primeiro instante t em que x(t) = 2 cm é t= 55 segundos. 08.A amplitude do movimento é 2 cm. 16. No intervalo de tempo [0,6], o corpo passa somenteduas vezes pela posição em que x(t) = 0. Gabarito: 13 12 28) A figura a seguir representa um sistema constituído por uma partícula de massa m, ligada a extremidade de uma mola de constante elástica k. A partícula é puxada desde a posição de equilíbrio 0 até a posição x e em seguida abandonada, realizando movimentos harmônicos simples, na ausência de forças dissipativas. Nessas condições, é correto afirmar 01. Surge, no sistema, uma força igual akx/2. 02. O período do movimento depende da massa da partícula e da constante elástica k. 04. Nos pontos de inversão do sentido do movimento, a aceleração da partícula é nula. 08. A energia mecânica do sistema é igual a 1 kx2/2. 16. Associando-se a mola em série com uma outra, de constante elástica k2, a freqüência de oscilação da partícula será igual a f 1 2 kk 2 k k 2 m Gabarito: 26 29) Uma partícula de massa m se move sobre um eixo em movimento harmônico simples, tendo sua elongação x dada por x =Asen(ωt) onde A é a amplitude, ω a pulsação e t o tempo de movimento. É correto afirmar que 01. (-1 < x/A < 1). 02. A elongação máxima da partícula é Aω. 04. O período de movimento da partícula é ω/2π 2 08. A energia da partícula é m.A2.ω /2. 2 16. A aceleração máxima da partícula é A2.ω . Gabarito: 09 30)Um sistema constituído por um bloco preso à extremidade de uma mola oscila livremente em um plano horizontal, e o valor algébrico da força resultante que atua no bloco varia com abscissa x, de acordo com o gráfico da figura abaixo. 01. A amplitude do movimento é 20 cm. 02.A constante elástica da mola é 3 N/cm. 04.Se o bloco tem massa de 3 Kg, podemos afirmar que a freqüência angular do movimentoé 10 rad/s. 08. A energia do sistema é 3 J. 16. A velocidade máxima ocorre no instante em que a aceleração é máxima, e vale 30cm/s. Gabarito: 06
Download