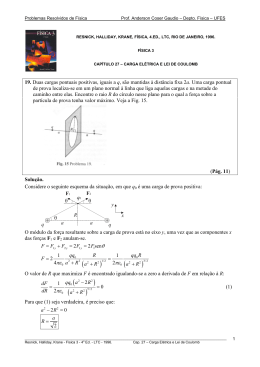
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 1
CAPÍTULO 8 – CONSERVAÇÃO DE ENERGIA
21. A mola de um revólver de brinquedo tem constante elástica de 7,25 N/cm. O revólver é
inclinado de 36,0o acima da horizontal e dispara uma bola de 78 g à altura de 1,9 m acima da
boca do revólver. (a) Qual a velocidade de saída da bola? (b) De quanto deve ter sido
comprimida inicialmente a bola?
(Pág. 161)
Solução.
Considere o seguinte esquema da situação:
C
y
vC
g
v0
B
h
θ
θ
x
A
m
d
k
Como o sistema é conservativo, vamos aplicar o princípio da conservação da energia mecânica aos
pontos B e C.
EB = EC
K B + U gB =K C + U gC
No ponto C o projétil tem velocidade vertical igual a zero e velocidade horizontal (que é a
velocidade do projétil) igual a v0 cos θ.
1 2
1
2
mv0 + 0
m ( v0 cos θ ) + mgh
=
2
2
=
v02 v02 cos 2 θ + 2 gh
v0
=
2 gh
10,3874 m/s
=
1 − cos 2 θ
v0 ≈ 10 m/s
(b) Aplicando-se o princípio da conservação da energia mecânica aos pontos A e B:
E A = EB
K A + U gA + U eA = K B + U gB + U eB
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 1 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação de Energia
1
Problemas Resolvidos de Física
1 2 1 2
=
0 − mgd sen θ + kd
mv0 + 0 + 0
2
2
Prof. Anderson Coser Gaudio – Depto. Física – UFES
 2
× 
 k
mv 2
2mg sen θ
0
d− 0 =
k
k
As raízes desta equação são:
d1 = 0,108364
d2 −
d 2 = −0,107123
Como d > 0:
d1 ≈ 0,11 m
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 1 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação de Energia
2