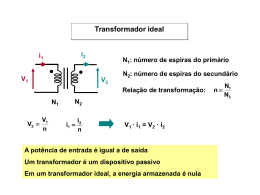
Transformadores monofásicos
 Motivações.
 Introdução.
 Transformador ideal.
 Transformador real.
 Circuito equivalente.
 Determinação dos parâmetros do circuito equivalente.
 Rendimento.
Motivações
 Por que precisamos estudar este tópico?
 Os transformadores permitem a transmissão a grandes
distâncias usando altos níveis de tensão e reduzindo as perdas
elétricas dos sistemas.
 Entender os aspectos básicos do campo magnético que
estabelecem os fundamentos da operação dos transformadores.
 Desenvolver circuitos equivalentes que representem o
comportamento dos transformadores.
Fotos
Fotos
Transformador utilizado para realizar casamento de impedância em
circuito impresso.
Fotos
Transformador utilizado em sistemas de distribuição (alimentação
da rede secundária)
Fotos
Corte em um transformador
(bobinas, buchas, radiador)
Fotos
Transformador utilizado em subestação de sistemas de distribuição
(cerca de 3,5 metros de altura)
Fotos
Transformador utilizado em
subestação de sistemas
industriais
Fotos
Transformador
utilizado em
sistemas de
transmissão
Fotos
Transformadores utilizado em sistemas de transmissão
Introdução (1/6)
 O transformador é comumente utilizado em sistemas de conversão
de energia e em sistemas elétricos.
 Seu princípio de funcionamento é baseado nas leis desenvolvidas
para análise de circuitos magnéticos.
 Transformadores são utilizados para transferir energia elétrica
entre diferentes circuitos elétricos através de um campo
magnético, usualmente com diferentes níveis de tensão.
Introdução (2/6)
 As principais aplicações dos transformadores são:
 Adequar os níveis de tensão em sistemas de geração,
transmissão e distribuição de energia elétrica.
 Isolar eletricamente sistemas de controle e eletrônicos do
circuito de potência principal (toda a energia é transferida
somente através do campo magnético).
 Realizar casamento de impedância de forma a maximizar a
transferência de potência.
 Evitar que a corrente contínua de um circuito elétrico seja
transferida para o outro circuito elétrico.
 Realizar medidas de tensão e corrente. Um transformador
pode fornecer isolação entre linhas de distribuição e
dispositivos de medição.
Introdução (5/6)
símbolo
 O transformador tem a função de transformar energia elétrica em c.a. de um
determinado nível de tensão para um outro nível de tensão através da ação de
um campo magnético.
 Esse dispositivo consiste de duas ou mais bobinas enroladas em um núcleo
ferromagnético.
 Normalmente, a única conexão entre essas bobinas é o fluxo magnético que
circula pelo núcleo ferromagnético (com exceção do autotransformador).
Exemplo da necessidade do uso de transformadores em sistemas de potência
Seja um gerador com tensão terminal de 10 kV e capacidade de 300 MW, e que se
deseja transmitir esta potência (energia) para um carga situada a um distância de 20
km.
Tem-se que:
If = Pf` / Vf
Sabemos que:
A
Pf = 300,0 MW
Vf = 10,0 kV
Assim, temos:
If = 300,0/10,0 = 30,0 kA
Exemplo da necessidade do uso de transformadores em sistemas de potência
 Sendo a resistividade do cobre  = 1,75 10-8 /m, a resistência será:
RL =  l/A

 Para l = 20 km e considerando que o condutor tem uma bitola de 25 mm2, temos:
RL = (1,75 10-8  20  103)/((25  10-3)2) = 0,1783 
 Assim, a perda ôhmica de potência (dissipada na LT) será:
Ploss = RL I 2 = 0,1783 (30,0)2= 160 MW
 Esta perda representa:
(160/300,0)  100 = 53,3%
Ou seja, mais da metade da potência (energia) gerada seria perdida na transmissão.
Uso de transformadores em sistemas de potência
Revisão (1/6)
 Produção de um campo magnético.
i
André-Marie Ampère
“Quando um condutor é percorrido por uma corrente elétrica surge
em torno dele um campo magnético”
 Lei circuital de Ampère.
  n
 H .dl   ik
c
k 1
Revisão (2/6)
Michael Faraday
Constatações:
 Ocorre um deslocamento do ponteiro do galvanômetro no instante
em que a chave é fechada ou aberta (fonte CC).
 Para corrente constante (chave fechada), independentemente de
quão elevado seja o valor da tensão aplicada, não há deslocamento
do ponteiro.
Revisão (3/6)
 Lei de Faraday.
fluxo 
e
Michael Faraday
Constatações:
 Ao se aproximar ou afastar o ímã do solenóide (bobina) ocorre um
deslocamento do ponteiro do galvanômetro.
 Quando o ímã está parado, independentemente de quão próximo
este esteja do solenóide, não há deslocamento do ponteiro do
galvanômetro.
Revisão (4/6)
 Lei de Faraday.
fluxo 
e
Michael Faraday
d
e
dt
 A lei de Faraday declara que:
“Quando um circuito elétrico é atravessado por um fluxo magnético
variável, surge uma fem (tensão) induzida atuando sobre o mesmo.”
 A lei de Faraday também declara que:
“A fem (tensão) induzida no circuito é numericamente igual à
variação do fluxo que o atravessa.”
Revisão (5/6)
 Lei de Faraday.
fluxo 
e
Michael Faraday
d
e
dt
Formas de se obter uma tensão induzida segundo a lei de Faraday:
 Provocar um movimento relativo entre o campo magnético e o
circuito.
 Utilizar uma corrente variável para produzir um campo magnético
variável.
Revisão (6/6)
 Lei de Lenz.
d
e
dt
Heinrich Lenz
“A tensão induzida em um circuito fechado por um fluxo magnético
variável produzirá uma corrente de forma a se opor á variação do
fluxo que a criou”
Principio de funcionamento (1/4)
 O que acontece se energizamos a bobina 1 com uma fonte de
corrente continua?
 O que observa a bobina 2?
Principio de funcionamento (2/4)
 O que acontece se energizamos a bobina 1 do transformador com
uma fonte de corrente alternada?
 O que observa a bobina 2 do transformador?
Principio de funcionamento (3/4)
 Pela lei de indução de Faraday, surge uma tensão induzida na
bobina 2 do transformador.
Principio de funcionamento (4/4)
 Se uma carga é conectada na bobina 2 do transformador, uma
corrente i2 circulará pelo mesmo.
 Pela lei de Lenz, o sentido da corrente i2 é de forma a se opor á
variação do fluxo magnético que a criou.
Transformador ideal
+
v1
–
+
e1
–
+
e2
–
+
v2
–
 Transformador ideal (sem perdas):
 A resistência dos enrolamentos são desprezíveis
 A permeabilidade do núcleo é infinita (portanto a corrente de magnetização
é nula)
 Não há dispersão
 Não há perdas no núcleo
Equação fundamental do transformador
 Equação fundamental do transformador
d

 v1  e1  N1 dt

v  e  N d 
2
2
 2
dt
 Em valor eficaz temos:
d
e1  N1
dt

E1  4,444 . N1 . f . Bm . A
d
dt

E 2  4,444 . N 2 . f . Bm . A
e2  N 2
E  4,444. N . f . Bm . A
Relação de transformação
 Considerando o transformador ideal em vazio (i2 = 0)
d

 v1  e1  N1 dt

v  e  N d 
2
2
 2
dt
 Desta forma temos:
d
v1 e1
N1
dt



a
v2 e2 N d N 2
2
dt
N1
Em que, a é relação de espiras do transformador, denominada
relação de transformação.
Primeira equação do transformador
 Tal relação é denominada relação de transformação.
 Para tensões senoidais, em termos de fasores, temos a primeira eq.
do transformador
V1 E1 N1


a
V2 E 2 N 2
Portanto:
V1  aV2
a 1

V2  V1

transformador elevador
a 1

V2  V1

transformador abaixador
Transformador - Princípio de Funcionamento
http://www.youtube.com/watch?v=CUllT-wEExU
Segunda equação do transformador
 Considerando uma carga no secundário, existirá uma corrente i2
no mesmo que cria uma força magneto – motriz N2i2 que tende a
alterar o fluxo no núcleo (desmagnetizando o núcleo).
 Portanto, o equilíbrio entre as forças magneto – motrizes será
perturbado.
 A segunda equação do circuito magnético de um transformador é
dada por:
N1i1  N 2i2  0
N1i1  N 2i2
Segunda equação do transformador
 Visto que N1i1 = N2i2, a única maneira do balanço se manter, é a
corrente i1 variar com o aumento de i2. Pode-se dizer que uma
fmm adicional é exigida do primário. Assim, temos:
i1 N 2 1


i2 N1 a
 Em termos fasoriais:
I1 N 2 1


I2 N1 a
2
I
I1 
a
 Obs: na análise acima, desprezamos a corrente de magnetização
(permeabilidade infinita), mas na prática é necessário uma
pequena corrente de magnetização no enrolamento primário para
estabelecer o fluxo no núcleo.
Balanço de potências
 A potência instantânea no primário é dada por:
p1 (t )  v1  i1
 A potência instantânea no secundário é dada por:
p2 (t )  v2  i2
 Sabemos:
i2
p1 (t )  v1  i1  av2   v2  i2  p2 (t )
a
 O que era esperado, visto que todas as perdas foram desprezadas.
Em termos fasoriais, temos:
*

I
S1  V1  I1*  aV2  2  V2  I2*  S 2
a
Em que S é a potência aparente (VA).
Valores referidos
 Ao se conectar uma impedância no secundário, qual a impedância
vista pelo primário?
I1
V1
I2
E1
E2
V2
 Temos que a impedância nos terminais do secundário é dada por:
V2
Z2 
I2
 Analogamente, a impedância equivalente vista dos terminais do
primário (vista pela fonte) é:

V1 aV2
2 V2
Z1  
a
 a 2 Z 2  Z 2
I1 I2 a
I2
Valores referidos
 A impedância conectada ao terminal do secundário produz no
primário o mesmo efeito que o produzido por uma impedância
equivalente Z 2 conectada aos terminais do primário. Z 2 é chamada
de impedância do secundário refletida ao primário.
I2
I1
I1
N :N
1
V1
Z 2'  a 2 Z 2
2
V1
Z 2  a 2 Z 2
 De maneira similar, as correntes e tensões podem ser refletidas de
um lado para o outro através da relação de espiras:
  N 2  I2
 I1  N I 2  a
1

V  N1 V  aV
2
 1 N 2 2
Exemplo: Casamento de impedância via transformador
Um auto falante tem uma impedância resistiva de 9 , o qual é conectado a uma fonte
de 10 V com impedância resistiva interna de 1 , como mostrado na figura abaixo:
9
1
auto
falante
10 V
(a) Determine a potência entregue pela fonte ao auto falante.
(b) Para maximizar a transferência de potência para o auto falante, um transformador
com uma relação de espira de 1:3 é usado para conectá-lo a fonte como mostrado
na figura abaixo. Determine a potência entregue pela fonte ao auto falante neste
caso.
1:3
1
10 V
9
auto
falante
Exemplo: Casamento de impedância via transformador
(a)
I = V/RT = 10/(1+9) = 1 A
P = R I2 = 9 12 = 9 W
9
1
auto
falante
10 V
(b) A impedância refletida ao primário é dada por:
R’2 = a2 . R2 = (1/3)2  9 = 1 
Portanto, temos:
I = V/RT = 10/(1+1) = 5 A
P = R I2 = 1  52 = 25 W
1:3
1
10 V
9
auto
falante
Transformador real (1/2)
 Um transformador ideal não apresenta perdas e toda potência
aplicada ao primário é entregue a carga. Algumas perdas são:
 Potência dissipada nos enrolamentos.
 Perdas por aquecimento do núcleo do transformador (por correntes
parasitas e histerese).
 Fluxo de dispersão (i.e., parte do fluxo deixa o núcleo e não concatena o
primário com o secundário).
 No transformador real:
 As resistências dos enrolamentos não são desprezíveis.
 A permeabilidade do núcleo é finita (haverá uma corrente de magnetização
não nula e a relutância do núcleo é diferente de zero).
 Há dispersão.
 Há perdas no núcleo (por correntes parasitas, histerese, ruído, magneto
estricção...).
Transformador real (2/2)
I1
V1
R1
X1
Ic
I
Rc
Im
I2

X m E1
R2
E 2
 R1  resistência do enrolamento do primário.
 R2  resistência do enrolamento do secundário.
 X1  reatância de dispersão do primário.
 X2  reatância de dispersão do secundário.
 Rc  representa as perdas no núcleo.
 Xm  reatância de magnetização (produz o fluxo).
 I  corrente de excitação
X 2 I2
V2
Circuito equivalente (1/8)
 Definindo-se:
Z1  R1  jX l1

impedância interna do primário
Z 2  R2  jX l 2

impedância interna do secundário
 Tem-se:
E1  V1  Z1 I1

E2  V2  Z 2 I2
 Portanto:
E1 N1

a
E2 N 2
 A relação de espiras é igual a relação entre as tensões induzidas
pelo fluxo mútuo nos enrolamentos primário e secundário.
Circuito equivalente (3/8)
I1
V1
R1
X1
Ic
Rc
I
Im
I2

X m E1
R2
X 2 I2
E 2
V2
 Em que:
E12
Rc 
: representa as perdas no núcleo
Pc
E12
Xm 
: reatância de magnetizaç ão (produz o fluxo)
Qm
Pc : perdas no núcleo (ferro) em W
Qc : potência reativa necessária para produzir o fluxo mútuo em VAr
Circuito equivalente (4/8)
 O modelo final é igual ao transformador ideal mais as
impedâncias externas representando as perdas.
 O circuito elétrico equivalente T é dado por:
I1
V1
R1
X1
Ic
Rc
I
Im
I2

X m E1
R2
E 2
X 2 I2
V2
Circuito equivalente (5/8)
 Refletindo as quantidades do secundário para o primário.
I1
R1
X1
V1
 Em que:
V2  aV2

  I2
I2 
a

 R  a 2 R
2
 2
 X 2  a 2 X 2
Ic
Rc
I
Im
Xm
R2
X 2' I2
V2
Polaridade dos enrolamentos do transformador
 Dois terminais são considerados de mesma polaridade quando
correntes entrando nesses terminais produzem fluxo na mesma
direção no núcleo magnético.
 Os terminais “1” e “3” têm polaridades iguais pois correntes que entram por
esses terminais produzem fluxo na mesma direção (sentido horário).
 Os terminais “2” e “4” também tem polaridades iguais, as correntes que entram
por esses terminais produzem fluxo na mesma direção (sentido anti-horário).
 Os enrolamentos de um transformador podem ser marcados para indicar os
terminais de mesma polaridade
Polaridade dos enrolamentos do transformador
 Convenção de pontos: Usualmente coloca-se um ponto nos
terminais das bobinas que sejam de mesma polaridade indicando a
forma como as bobinas estão enroladas no núcleo.
 Significa que um fluxo mútuo variável através das duas bobinas
produz tensões induzidas e12 e e34 em fase, ou seja:
e12 E12

a

e34 E34
Polaridade de Transformadores
http://www.youtube.com/watch?v=S4HfYKukF1Y
Rendimento (1/2)
 Os transformadores são projetados para operarem com alto
rendimento.
 Os seguintes aspectos contribuem para que os transformadores
apresentem valores baixos de perdas:
 O transformador é uma máquina estática, ou seja, não tem partes rotativas,
não apresentando, portanto, perdas por atrito no eixo e por resistência do ar
no entreferro.
 O núcleo é constituído por placas laminadas e dotadas de materiais de alta
resistência elétrica, as quais têm o objetivo de minimizar as perdas por
correntes parasitas.
 Materiais com alta permeabilidade magnética são utilizados para diminuir
as perdas por histerese.
 Transformadores de alta potência apresentam rendimento maior que 99 %.
Rendimento (2/2)
 O rendimento de um transformador pode ser definido por.
PSAIDA
PSAIDA


PENTRADA PSAIDA  PPERDAS
PENTRADA
TRAFO
PSAIDA
PPERDAS = PENTRADA  PSAIDA
 As perdas no transformador incluem:
 Perdas no núcleo (ferro) – PC (perdas por correntes parasitas e perdas por
histerese), podem ser determinadas pelo teste em vazio, ou a partir dos
parâmetros do circuito equivalente.
 Perdas no cobre – PCu (perdas ôhmicas), podem ser determinadas se os
parâmetros do transformador forem conhecidos (corrente nos enrolamentos
e resistência dos enrolamentos)

PSAIDA
PSAIDA

PENTRADA PSAIDA  PC  PCu
Regulação de tensão (1/1)
 Um dos critérios de desempenho de um transformador projetado
para suprir potência com tensão aproximadamente constante para
uma carga é o de regulação de tensão.
 Tal critério indica o grau de constância da tensão de saída quando
a carga é variada.
 A regulação de tensão do transformador é definida como sendo a
variação da tensão do secundário em condições de plena carga
e em vazio, tomada como porcentagem da tensão a plena carga,
com tensão do primário mantida constante, ou seja:
Regulação em % 
V2, vazio  V2,plena carga
V2,plena carga
100
Exercicios
1. Explique forma simples a lei de indução de Faraday e para que é
utilizado.
2. Usando lei circuital de Ampère e a lei de indução de Faraday,
explique o principio de funcionamento de um transformador.
3. Por que é importante o transformador em um sistema de energia
elétrica.
4. Por que é importante desenvolver um circuito equivalente que
represente o comportamento do transformador em regime
permanente.
5. Desenhe o circuito equivalente T do transformador, identifique e
explique o que representa cada um de seus componentes.
Determinação dos parâmetros do circuito equivalente (1/4)
 Os parâmetros do circuito equivalente podem ser determinados
através de dois testes chamados teste em vazio e teste de curtocircuito.
 Teste em vazio:
 No teste em vazio, o lado de alta tensão do transformador é deixado em
aberto e uma tensão nominal na freqüência nominal é aplicada no lado de
baixa tensão.
 Usualmente, a tensão nominal é aplicada ao lado de baixa tensão no teste
em vazio por este ter um menor valor de tensão nominal.
 Então, mede-se a tensão, a corrente e a potência ativa nos terminais do lado
de baixa tensão.
 Neste caso, a corrente do lado de baixa tensão é composta somente pela
corrente de excitação.
Determinação dos parâmetros do circuito equivalente (2/4)
A
I0
W
P0
V V0
 Portanto temos:
I
Ic
Im
Rc
R1  R2
Xm

V02
 Rc  P
0

V0

I c  R
c

I  I 2  I 2
0
c
 m

V0
X m  I

m
X 1  X 2
Determinação dos parâmetros do circuito equivalente (3/4)
 Teste em curto-circuito:
 No teste de curto-circuito, o lado de baixa tensão é curto-circuitado e a
tensão aplicada ao lado de alta tensão é gradualmente aumentada até se
obter a corrente nominal no lado de alta tensão.
 Usualmente, uma corrente nominal é aplicada ao lado de alta tensão no
teste de curto-circuito por este ter um menor valor de corrente nominal
 Então, mede-se a tensão, a corrente e a potência ativa nos terminais do lado
de alta tensão.
 Visto que foi curto-circuitado o lado de baixa tensão o ramo de excitação
pode ser desprezado.
Determinação dos parâmetros do circuito equivalente (4/4)
R1  R2
Rc
Xm
X 1  X 2 I2
Req  R1  R2
X eq  X 1  X 2
 Portanto temos:

2 Pcc
 Req  a I 2
cc


2 Vcc
Z eq  a
I cc

X  Z 2  R2
eq
eq
 eq

V2
I2
V2 Vcc V
W
Pcc
A
I cc
Exemplo
A partir de testes realizados em um transformador monofásico de 10 kVA, 2200/220 V,
60 Hz, os seguintes resultados são obtidos:
teste em vazio
teste de curto-circuito
Voltímetro:
220 V
150 V
Amperímetro:
2,5 A
4,55 A
Wattímetro:
100 W
215 W
(a) calcule os parâmetros dos circuito equivalente referidos ao lado de baixa e alta
tensão.
(b) expresse a corrente de excitação em termos da corrente nominal.
Exemplo
(a) O teste em vazio foi realizado aplicando-se tensão nominal ao lado de baixa tensão.
Assim, temos:
- Perdas no núcleo:
V02
V02 2202
P0 
 Rc 

 484 
Rc
P0
100
- Corrente de perdas:
Ic 
V0 220

 0,45 A
Rc 484
- Corrente de magnetização:
I   I 0  2,5
A
I m  I 2  I c2  2,5 2  0,452  2,46 A
- Reatância de magnetização:
Xm 
V0
220

 89,4 
I m 2,46
Exemplo
Referido ao lado de baixa:
Rc = 484  e Xm = 89,4 
Referido ao lado de alta (a = VH/VL = 2200/220 = 10):
Rc = 48.400  e Xm = 8.940 
O teste de curto-circuito foi realizado aplicando-se tensão no lado de alta tensão até
obter corrente nominal (10 kVA/2.2 kV = 4,55 A). Assim, temos:
2
Pcc  Req I cc
 Req 
Z eq 
Pcc
2
I cc

215
2
4,55
 10,4 
Vcc 215

 32,97 
I cc 4,55
2
2
X eq  Z eq
 Req
 32,972  10,4 2  31,3 
Referido ao lado de alta:
Req = 10,4  e Xeq = 31,3 
Referido ao lado de baixa (a = VL/VH = 220/2200 = 0,1):
Req = 0,104  e Xeq = 0,313 
Exemplo
Referido ao lado de alta:
10,4 
48.400 
Referido ao lado de baixa:
484 
31,3 
8.940 
0,104 
89,4 
0,313 
Exemplo
(b) expresse a corrente de excitação em termos da corrente nominal
No teste em vazio, a corrente medida é igual a corrente de excitação. Além disso, o
teste é realizado do lado de abaixa, assim, temos:
I
In

2,5
2,5
 100 
100  5,5%
(10.000VA / 220V)
45,5