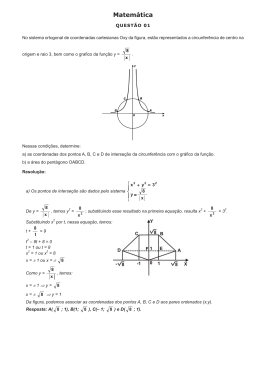


 


















COMENTÁRIO DA PROVA - MATEMÁTICA
 
 
 
 



COMENTÁRIO - ASSUNTO: GEOMETRIA PLANA



Considere a figura:
























Como o trapézio ABCD é isósceles, segue que:
• PQ = CD = 9 m
15 − 9
• AP = BQ =
m=3m
2
Por outro lado, observe que o triângulo BDT é retângulo em T de lados:
• BD = 15 m
• BT = h (altura do trapézio)
• DT = DC + CT = DC + BQ = 12 m
Logo, pelo Teorema de Pitágoras, temos:
(BD)2 = (BT)2 + (DT)2
152 = h2 + 122
h2 = 81 ∴ h = 9 m.
Assim, a área do trapézio ABCD é:
(AB + CD) . BT (15 + 9) . 9
= 108m2
=
[ ABCD] =
2
2

Item: C


