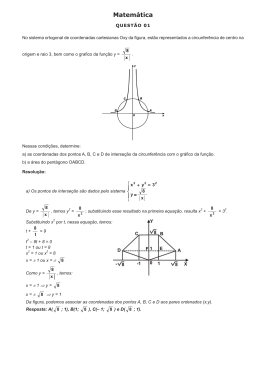
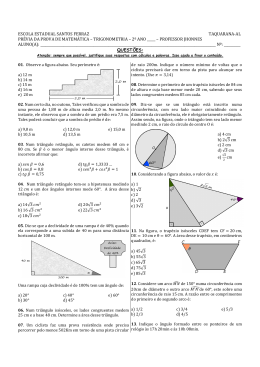
▼
Questão 4
— —
A figura representa um trapézio ABCD de bases AB e CD, inscrito em uma circunferência cujo centro O está no
interior do trapézio.
Sabe-se que AB = 4, CD = 2 e AC = 3 2.
C
D
O
B
A
a) Determine a altura do trapézio.
b) Calcule o raio da circunferência na qual ele está inscrito.
c) Calcule a área da região exterior ao trapézio e delimitada pela circunferência.
Resolução
Do enunciado, temos a figura, em que o trapézio ABCD é isósceles:
2
D
C
AC = 3 2;
h
O
α
A
E
1
B
F
2
DE = CF = h;
DA = CB;
0º α 90º.
1
a) Aplicando o teorema de Pitágoras no triângulo retângulo CAF, temos:
(CF)2 + (AF)2 = (AC)2 ∴ h2 + 32 = (3 2 )2
∴ h=3
Resposta: 3
b) No triângulo retângulo ACF, temos:
CF
3
(I)
∴ tgα = = 1 ∴ α = 45º
AF
3
Aplicando o teorema de Pitágoras no triângulo retângulo CFB, temos:
tgα =
(CB)2 = (CF)2 + (FB)2 ∴ (CB)2 = 32 + 12 ∴ CB =
10
(II)
Sendo r a medida do raio da circunferência de centro O e aplicando o teorema dos senos ao triângulo CAB, temos:
CB
(III)
senα
De (I), (II) e (III), temos:
2r =
2r =
10
10
∴ 2r =
sen 45º
2
2
Resposta:
∴ r= 5
5
1
c) A área S pedida pode ser obtida fazendo-se a área do círculo de centro O e raio medindo
do trapézio ABCD. Logo:
( 4 + 2) ⋅ 3
S = π ⋅ ( 5 )2 –
∴ S = 5π – 9
2
Resposta: 5π – 9
2
5 menos a área