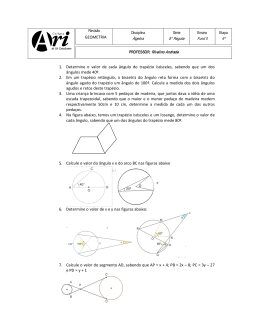
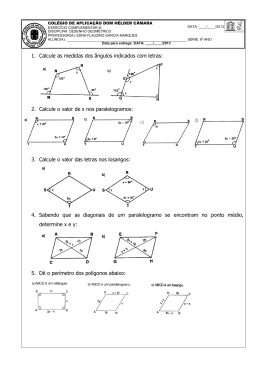
Plantão de Matemática
Fabrízio
8º
19 e 20/MAI
Lista de exercícios nº 13
1. Dados os polinômios A  5 x 2  3x  4 , B  2 x 2  4 x  3 e C  x 2  3x , calcule:
a) A – B
b) B – A
c) A + C – B
2. Dados os polinômios A  2 y 3  4 y 2  10 e B  y 3  y 2  4 y  8 , calcule o polinômio X, de modo que:
a) A – B = X
b) X = A + B
c) X – A = B
d) X + B = A
3. Calcule os produtos.
a) (2x + 3) . (3x + 5)
b) (2y + 1) . (2y – 1)
c) (5x2 – 7x + 8) . (– 4x – 3)
d) (x + 1) . (x2 – x + 1)
R.:
R.:
R.:
R.:
6x2 + 19x + 15
4y2 – 1
– 20x3 + 13x2 – 11x – 24
x3 + 1
4. Determine o polinômio P que, dividido por (x – 2), tenha por quociente exato (2x + 3).
5. Determine os quocientes abaixo:
a) (12x2 + 9x) : 3x
b) (21x3 – 14x2 + 7x) : 7
c) (6a2x – 9ax2 – 12a) : 3a
d) (12x2y – 9xy2 + 15xy) : (– 3xy)
R.: 2x2 – x – 6
R.: 4x + 3
R.: 3x3 – 2x2 + x
R.: 2ax – 3x2 – 4
R.: – 4x + 3y – 5
6. Um dos ângulos agudos de um trapézio isósceles mede 55º. Calcule a medida dos demais ângulos desse
trapézio. R.: 55º, 125º e 125º
7. As bases de um trapézio medem 20 cm e 12 cm. Quanto mede a base média do trapézio? R.: 16 cm
8. O maior ângulo de um trapézio retângulo tem por medida o dobro da medida do menor ângulo. Calcule as
medidas dos ângulos internos desse trapézio. R.: 60º, 90º, 90º e 120º
9. A base média de um trapézio isósceles mede 30 cm. Cada um dos lados congruentes mede 10 cm. Calcule o
perímetro desse trapézio. R.: 80 cm