Colégio Naval
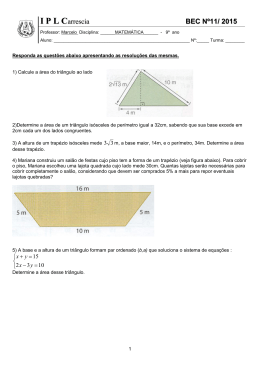
Matemática - 1987
1. Representando-se por n(X) o número de elementos de
um conjunto X, considere dois conjuntos A e B tais que n
(A  B) = 4, n(A – B) = 5 e n(A x B) = 36. Podemos afirmar
que n(A  B) é igual a:
(A) 4
(B) 6
(C) 7
(D) 9
(E) 10
2. Considere os conjuntos X = {x  IN/ x  4} e y, y  x. O
número de conjuntos y tais que 4  y e 0  y é:
(A) 6
(B) 7 (C) 8
(D) 15
(E) 16
3. A media harmônica entre as raízes da equação
2
340x – 13x – 91 = 0 é:
340
1
(A) 7
(B) –7
(C)
(D)
(E) – 14
7
7
4. O número máximo de divisores do número natural
2
48. 2-x 2x , x   , é
(A) 12
(B) 10
5. O valor de x no sistema
(C) 24
(D) 6
(E) 18
16x  y  1
é:

4
 x  2  x  33  1
(A) 15 + 14 2
(B) 15 + 12 2
(C) 15 + 10 2
(D) 15 + 8 2
(E) 15 + 6
2
6. Uma mercadoria foi comprada por Cr$ 20.000. Para que
haja um lucro de 60% sobre o preço de venda, essa
mercadoria deve ser vendida por:
(A) Cr$ 32.000
(B) Cr$ 50.000
(C) Cr$ 48.000
(D) Cr$ 45.000
(E)
Cr$
58.000
3
a
7. O valor da expressão E = 9a – 3 , para
1

51.(33  32 ( 2)3 )  2
a   0,2666... 

(0,333...)3.(5) 

(A)
3
(B)

2
(C)
5
5
5
4
(D) 0
3
2
(E) 1
8. O resto da divisão de ( x + x – 5x – x + 9x – 8) por (x
+ x – 3) é:
(A) independente de x e não nulo
5
(B) positivo para x <
2
(C) nulo
(D) par, para x  N
(E) igual a 21, para x = 13
2
9. O número
(A) 1 e 1,5
(D) 2, 5 e 3
1  3 4  3 16
(B) 1, 5 e 2
(E) 3,5 e 4
está situado entre:
(C) 2 e 2,5
10. Sendo P e Q dois polinômios de mesma variável e de
graus respectivamente iguais a m e n, e sendo m  n,
podemos afirmar que:
(A) a soma de P e Q é de grau m + n
(B) o produto de P por Q é de grau m.n
(C) a soma de P e Q é de grau m
(D) o quociente entre P e Q. caso existe é de grau m – n
(E) a diferença entre P e Q é de grau n
11. Duas pessoas constituíram uma sociedade entrou com
um capital de Cr$ 5.000.000 e a Segunda com Cr$
6.000.000. Um ano depois, admitiram um terceiro sócios,
que entrou com um capital de Cr$ 10.000.000. Decorridos
18 meses desde o início da sociedade, a firma teve um
lucro de Cr$12.000.000. A parte do lucro que caberá ao
terceiro sócio é
Obs: o lucro é dividido proporcionalmente ao capital e ao
tempo, não se levando em conta outros fatores, como por
exemplo a inflação.
(A) Cr$ 1.000.000(B) Cr$ 2.000.000
(C) Cr$ 3.000.000 (D) Cr$ 4.000.000
(E) Cr$ 5.000.000
y  x2
12. O sistema 
y  x  2

(A) não tem solução
(B) tem solução contida no 4º quadrante
(C) tem solução que contém o 2º quadrante
(D) é satisfeito por apenas um ponto do plano cartesiano
(E) tem solução apenas para y 2
13. Um vendedor de refresco acondiciona o seu produto
numa caixa de isopor com as seguintes dimensões
internas: 1m x 60cm x 40cm. Cada copo de refresco de
300ml é vendido por Cr$ 400. Nessas condições, ao
término de um dia de trabalho, pela venda de uma
3
quantidade de refresco correspondente a
da
4
capacidade da caixa, o vendedor apurou.
(A) Cr$ 360.000
(B) Cr$ 300.000
(C) Cr$ 270.000
(D) Cr$ 330.000
(E) Cr$ 240.000
14. o retângulo ABCD da figura abaixo tem base igual a x +
2
2
2
y. O segmento AF tem medida z. Sabe-se que x + y + z =
3,54 e que xz + yz – xy = 0,62. A área do quadrado FBCE é:
1|Projeto Futuro Militar – www.futuromilitar.com.br
(A)
(B)
(C)
(D)
(E)
16
14
12
8
20
E
D
A
20. Em um triângulo os lados de medidas m e n são
opostos, respectivamente, aos ângulos de 60º e 40º. O
segmento da bissetriz do maior ângulo interno do
triângulo é dado por:
C
(A) m
mn
n
(B) n
(D) n
m
mn
(E)
B
F
15. Na figura abaixo, as retas r, s e t são tangentes à
circunferência de diâmetro AB . O segmento AC mede 4
cm. A medida, em centímetros, do segmento CD é:
(A) 16
(B) 14
D
(C) 12
60º
C
(D) 8
(E) 20
t
A
mn
m
(C) m
n
mn
m
n
21. Considere um ponto P interno a um hexágono regular
de lado igual a 6 cm. A soma das distâncias de P a cada
uma das retas suportes dos lados desse hexágono.
(A) depende da localização de P
(B) é igual a 36 cm
(C) é igual a 18 cm
B
(D) é igual a 12 3 cm
(E) é igual a 18 3 cm.
r
22. A figura abaixo tem-se: QB e QA são tangentes ao
s
16. O trapézio ABCD da figura é retângulo. A bissetriz do
ângulo  intercepta BC no seu ponto médio M. A altura
do trapézio é igual a:
(A) 2 15
6
D
C
(B) 8 15
(C) 6 15
circulo de raio 2 a medida do segmento PA é 2 3 e a
potência do ponto P em relação ao circulo é igual a 24. A
área hachurada da figura é igual a:
(A)
(B)
(D) 4 15
M
(C)
(E) 5 15
A
10
B
17. O número de triângulo de perímetro igual a 19 e uma
das alturas igual a 4, inscritível num circulo de raio 5, e
cujos lados têm medidas expressas por números inteiros é:
(A) 1
(B) 2 (C) 3
(D) 4(E) 5
18. As bases de um trapézio medem 3 cm e 9 cm. Os
segmentos determinados pelas diagonais do trapézio
sobre a base media, são proporcionais aos números:
(A) 1, 1, 1
(B) 1, 2, 1
(C) 1, 3, 1
(D) 1, 4, 1
(E) 2, 3, 4
19. o intervalo solução da inequação (x+3) (x+2) (x–3) >
(x+2) (x–1) (x+4) é:
-5
5
(A) (  , )
(B) ( - , - 1 )
(C) (-2,
)
3
3
5
(D) (
, )
(E) –1, 2)
3
(D)
(E)
4
( 2 3  )
3
4
(3 3  )
3
4
( 3  )
3
4
( 4 3  )
3
4
( 6 3  )
3
Q
A
P
B
4
3
23. O maior divisor comum dos polinômios x – 16, x – 6x
4
2
+ 12x – 8 e x – 8x + 16 é:
(A) x + 2 (B) x + 4 (C) x – 2
(D) x – 4 (E) 1
24.
Uma
equação
biquadrada
tem
duas
2
raízes
respectivamente iguais a 2 e 3. O valor do coeficiente
do termo de 2º grau dessa equação é:
(A) 7
(B) – 7
(C) 11
(D) – 11
(E)1
25. Num triângulo ABC de lado AC = 12, a reta AD divide
internamente o lado BC em dois segmentos: BD = 18 e
DC = 6. Se AB̂D = x e AĈD = y, o ângulo BD̂A é dado
por
(A) y – x (B) x + y (C) 2x – y
(D) 2y – x (E) 2x + y
2|Projeto Futuro Militar – www.futuromilitar.com.br
Gabarito
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
D
C
E
A
B
B
D
E
C
D
C
A
E
C
A
D
A
B
C
C
E
B
C
D
B
3|Projeto Futuro Militar – www.futuromilitar.com.br