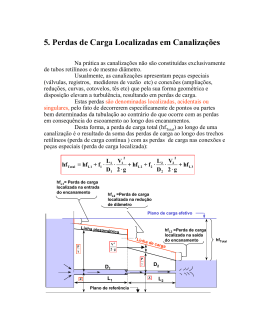
Aula 8
Perda de Carga Localizada
Exemplo 3.2
Uma mangueira de P.V.C., com L=50m de comprimento e D=50mm
de diâmetro, é ligada a um hidrante no qual a pressão é constante.
Um bocal, segundo a forma de uma contração brusca, é acoplado à
extremidade de saída para aumentar a energia cinética e
proporcionar ao jato d’água um alcance maior. Supondo que o
coeficiente de atrito na mangueira seja constante e igual a f=0,020 e
que o coeficiente de perda localizada no bocal, com relação ao
trecho de menor diâmetro, segue os valores tabelados abaixo,
determine o diâmetro d do bocal para qual se obtém o maior alcance
do jato livre.
(d/D)2 0,1
K
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
226 47,8 17,5 7,8
3,8
1,8
0,8
0,3
0,09 0
50mm
Exemplo 3.2
50m
D
Q
d
Exemplo 3.2
Aplicando Bernoulli entre hidrante (seção 1) e saída do bocal
(seção 2). Considerando; no mesmo nível, todas as perdas e a
carga cinética no hidrante sendo desprezada, tem-se:
2
p1 V22
V22
L Vmg
V22

 H  h 
f
K
 2g
2g
D 2g
2g
Pela continuidade:
2
d
d
Vmg  Vbocal    V1  V2  
D
D
2
4


p1 V
Ld V
V
V
d

f  
K

1  20   K 
 2g
D  D  2g
2g 2g 
D

2
2
4
2
2
2
2
2
2
Exemplo 3.2
Pela condição do problema, a pressão no hidrante é cte e o alcance
do jato deve ser máximo, isto é, quando a velocidade de saída V2 for
máxima o termo entre colchetes passará por um valor mínimo assim:
(d/D)2
0,2
0,3
K
47,8
17,5
[1+20(d/D)4+K]
49,6
20,3
0,4
0,5
7,8
3,8
12,0
9,8
0,6
0,7
1,8
0,8
10,0
11,6
d
 0,5  0,707
D
d  0,707* 50  35,35mm
Método dos Comprimentos Equivalentes
Le V 2
V2
h  K
 H  f
2g
D 2g
Le K

D f
3.15
3.16
Para tubos metálicos, aço galvanizado e ferro fundido tem-se
Le    D
Le 
 
D D
Comprimento Equivalente (Le)
Le em n0 de diâmetro de canalização (metálicas, ferro galvanizado e ferro
fundido)
Acessório
Equação
Figura
CE (Le/D)
(n0 de diâmetros)
Cotovelo 900
raio longo
Le=0,068+20,96D
22
Cotovelo 900
raio médio
Le=0,114+26,56D
28,5
Cotovelo 900
raio curto
Le=0,189+30,53D
34
Cotovelo 450
Le=0,013+15,14D
15,4
Curva 900
R/D=1,5
Le=0,036+12,15D
12,8
Comprimento Equivalente (Le)
Le (m) P.V.C rígido ou cobre, conforme A.B.N.T
Dext(mm)
Ref.
25-3/4
Joelho Joelho Curva Curva Tê 900 Tê 900
900
450
900
450
Direto Lateral
1,2
0,5
0,5
0,3
0,8
2,4
32-1
1,5
0,7
0,6
0,4
0,9
3,1
40-11/4
2,0
1,0
0,7
0,5
1,5
4,6
3,5m
1,2m
Na figura a seguir a
tubulação é P.V.C rígido,
soldável, com 1” de
diâmetro, e é percorrida
por uma vazão de 0,20l/s
de água. Os joelhos são
de 900 e os registros de
gaveta, abertos. No ponto
A 2,10m abaixo do
chuveiro, a carga de
pressão é igual a 3,3mca.
Determine a carga de
pressão disponível
imediatamente antes do
chuveiro. Os tês estão
fechados em uma das
saídas.
0,9m
Exemplo 3.3
0,2 l/s
3,0m
A p(3,3mca)
Exemplo 3.3
Acessório
3 Joelho 900
2 Registro gaveta aberto
Comprimento Equiv. (m)
3*1,5=4,5
2*0,3=0,6
Tê passagem direta
Tê lateral
Comprimento real da linha
0,9
3,1
8,6
Comprimento total
17,7
C.Pch  C.PA  Ht
3,3  Q1,75Lt  C.Pch C.Pch  3,3  0,1202 0,21,75 17,7  3,17m
Eq.2.48
p ch
 3,17  2,10  1,07m.c.a

Exemplo 3.4
Na instalação hidráulica predial mostrada na figura a seguir, as
tubulações são de aço galvanizado novo, os registro de gaveta são
abertos e os cotovelos têm raio curto. A vazão que chega ao
reservatório D é 38% maior que a que escoa contra a atmosfera no
ponto C. Determine a vazão que sai do reservatório A,
5,0
desprezando as cargas cinéticas.
3,0
A
0,3m
11/2”
1,0m
D
11/2”
6,0m
B
1,0m
1”
C
6,0m
Exemplo 3.4
H BD  X  3,0
H BC  X  1,0
HBC  HBD  2,0
J BC  LBC  J BD LBD  2,0
Exemplo 3.4
Trecho BD
Acessório
Trecho BC
Acessório
Comp.
Equi (m)
Comp. Equi
(m)
Tê Lateral (1 ½”)
2,587
Tê lateral (11/2”)
2,587
2 cotovelos 900
2,550
Reg. Gaveta
0,175
Reg. Gaveta
0,263
Saída
canalização
Comp. Real
0,775
1,133
6,00
Saída
canalização
Comp. Real
Comp. Total
9,54
Comp. Total
13,83
7,30
Exemplo 3.4
QBD  1,38QBC
3,044101 Q1BD,88  3,945102 1,38QBC 
1,88
13,83  2,0
2,904Q BD  0,9996Q BC  2,0  QBC  1,03 / s
1,88
1,88
QBD  1,42 / s
QBC  QBD  2,45 / s
Problema 3.4
Em um distrito de irrigação, um sifão de 2” de diâmetro possui as
dimensões indicadas na figura e é colocado sobre um dique.
Estime a vazão esperada sob uma carga hidráulica de 0,50m e a
carga de pressão disponível no ponto médio do trecho horizontal
do sifão. Adote os seguintes coeficientes de perda localizada:
entrada Ke = 0,5, saída Ks = 1,0 curva 450 K = 0,2. Material da
tubulação ferro fundido com revestimento asfáltico. Utilize a
equação de Darcy-Weisbach.
1,2m
50,5
50,0
0,5m
49,5
Problema 3.4
Estimativa da velocidade média
1a aproximação (sem perdas localizadas)
H 0,5
J

 0,1042m / m  10,42m / 100m
L
4,8
Ferro fundido
  0,12mm
Tabela A2
D = 50 mm
J = 10,42 m/100m
J
0,203Q 2 / gD 5
  
5,74 
log 3,7 D  Re 0,9 

 
2
V  2,0m / s
Problema 3.4
2a aproximação (com perdas localizadas)
L V2
V2
V2
4,8
Z  H  f
 K
Z  0,5 m 
[f
1,9 ]
D 2g
2g
19,6 0,050
Z  0,50  V2[ 4,898 f  0,0969]
Tabela A1 ou
Se V = 2,0m/s
f
f = 0,0263
0,25
  
5,74 
log 3,7D  Re 0,9 

 
Se V = 1,5m/s Tabela A1
2
f = 0,0268
Z = 0,902 m

0,50 m
Z = 0,513 m  0,50 m
Problema 3.4
Se f = 0,0268
Z  0,5  V2[ 4,898 f  0,0969]
Se V = 1,48m/s
Q  VA
Eq. Energia
Ok!! Tabela A1
0,052
Q  1,48
 0,0029m3 / s  2,9 / s
4
P V2
50,0  
 z  H t

2g
P 1,482
2,4 1,482
1,482
50,0 

 50,5  0,0268
 0,70

19,6
0,05 19,6
19,6
P
 0,83mca
