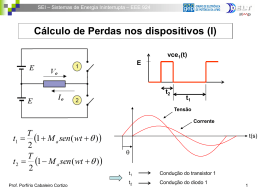
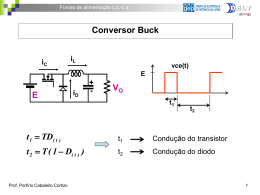
Fontes de alimentação c.c.-c.a
Modelamento do conversor
Modelamento não linear e não medianizado:
• simulação muito precisa e lenta (pequenos e grandes sinais)
• Difícil projeto do regulador
Modelamento não linear e medianizado:
• simulação precisa e rápida (pequenos e grandes sinais)
• Difícil projeto do regulador
Modelamento linear e medianizado:
• simulação menos precisa e rápida
• só pequenos sinais
• Fácil projeto do regulador
Prof. Porfírio Cabaleiro Cortizo
1
Fontes de alimentação c.c.-c.a
Em todos métodos de modelamento:
O primeiro passo sempre é identificar os
subcircuitos lineares que contínuamente
estão variando no tempo. Há dois casos:
• Modo de condução continuo (mcc):
dois subcircuitos
•Modo de condução descontínuo (mcd):
três subcircuitos
Prof. Porfírio Cabaleiro Cortizo
2
Fontes de alimentação c.c.-c.a
Exemplo I: Conversor buck em mcc
iS
iL
IO
comando
e
t
vO
iD
iL
IO
t
iS
iL
e
+
- vO
Durante d·T
iL
+
- vO
Durante (1-d)·T
t
iD
t
d·T
T
Prof. Porfírio Cabaleiro Cortizo
3
Fontes de alimentação c.c.-c.a
Modelamento não linear e não medianizado
Possibilidades:
• Simular em um programa tipo PSPICE o circuito real.
• Resolver intervalo a intervalo as equações dos
subcircuitos lineares.
Exemplo:
iL
e
+ vO
-
Durante t1
iL
+ vO
-
Durante t2
iL
e
+ vO
-
Durante t3
iL
+ vO
-
Durante t4
Conversor buck em mcc
Seguindo esta técnica podemos simular o comportamento do circuito
de potência no domínio do tempo. A informação será exata, mas
difícilmente aplicável ao projeto do regulador.
Prof. Porfírio Cabaleiro Cortizo
4
Fontes de alimentação c.c.-c.a
Modelamento não linear e medianizado
Idéia fundamental: “sacrificar” a
informação do que ocorre a nivel
de cada ciclo de comutação para
conseguir um tempo de simulação
muito menor.
d
t
iL
medianizado
t
Em particular, as variavéis elétricas que
variam pouco em cada ciclo de
comutação (variáveis de estado) são
sustituídas por seus valores médios. As
variáveis elétricas nos semicondutores
também
são
(de
alguma
forma)
medianizadas.
Prof. Porfírio Cabaleiro Cortizo
vO
valor medianizado
t
5
Fontes de alimentação c.c.-c.a
Métodos modelamento não linear e medianizado
Método da medianização de circuitos:
Se medianizam os subcircuitos lineares, que previamente se
reduzem a uma estrutura única baseada em transformadores.
Método da medianização de variáveis de estado:
Se medianizam as equações de estado dos subcircuitos
lineares.
Método do interruptor PWM (PWM switch):
O transistor é sustituído por uma fonte dependente de
corrente e o diodo por uma fonte dependente de tensão.
Prof. Porfírio Cabaleiro Cortizo
6
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 1: Descrever as variáveis de estado para cada subcircuito
Transistor ligado
Durante d.T

Diodo em condução
Durante (1-d)T

x  A1 x  B1u
x  A2 x  B2 u
y  C1 x  F1u
y  C 2 x  F2 u
Prof. Porfírio Cabaleiro Cortizo
7
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 2: Medianizar as variáveis de estado usando o ciclo de
trabalho
A   A1d  A2 ( 1  d )
B  B1d  B2 ( 1  d )
C  C1d  C 2 ( 1  d )
F  F1d  F2 ( 1  d )
Prof. Porfírio Cabaleiro Cortizo

x  Ax  Bu
y  Cx  Fu
8
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 3: Introduzir pequenas perturbações c.a.
Como o modelo é não linear, linearizamos em torno de um ponto de operação,
introduzindo pequenas perturbações:
xX~
x
y  Y  ~y
Prof. Porfírio Cabaleiro Cortizo
~
uU u
~
d  Dd
9
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 4a: Reescrever as equações de estado levando em conta
as pequenas perturbações
X  ~x   A ( D  d~ )  A ( 1  D  d~ )X  ~x  B ( D  d~ )  B ( 1  D  d~ )U  u~

1

 
2
1

2
 

~
~
~
~
~
~
~
Y  y  C1 ( D  d )  C 2 ( 1  D  d ) X  x  F1 ( D  d )  F2 ( 1  D  d ) U  u
Prof. Porfírio Cabaleiro Cortizo
10

Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 4b: Desenvolvendo as equações das~ variáveis
de estado e
~
~ são desprezíveis,
xed u
considerando que os termos de segunda ordem d ~
temos:

X  ~x   A X  A~x   A1  A2 X d~  BU  Bu~  B1  B2U d~
Y  ~y   C X  C ~x  C1  C 2 X d~  FU  F u~  F 1  F 2U d~
Prof. Porfírio Cabaleiro Cortizo
11
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 5: Separar as componentes c.c. e c.a.
TERMO c.c.
X   0  A X  BU
X   A1 BU
Y   C X  F U
Y   CA 1 B  F U

Prof. Porfírio Cabaleiro Cortizo


12
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 6a: Separar a componente c.a. e resolver no domínio da
freqüência
TERMO c.a. – Influência das variações da tensão de entrada

~
x  A~
x  Bu~
s~
x  A~
x  Bu~
sI  A~x  Bu~
~
x  ( sI  A )1 Bu~

~y  C sI  A1 Bu~  Fu~
Prof. Porfírio Cabaleiro Cortizo
~
y  C( sI  A )1 B  F u~
13
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 6b: Separar a componente c.a. e resolver no domínio da
freqüência
TERMO c.a. – Influência das variações da razão cíclica

~
~
x  A~
x    A1 - A2  X   B1  B 2  U  d
sI  A ~x    A1  A2  X  B1 - B2  U  d~
~
~
x  ( sI  A )1  -  A1 - A2  A-1 B  B1  B 2  U d
Prof. Porfírio Cabaleiro Cortizo
14
Fontes de alimentação c.c.-c.a
Método da medianização das Variáveis de Estado
Passo 6c: Separar a componente c.a. e resolver no domínio da
freqüência
TERMO c.a. – Influência das variações da razão cíclica
~
~
~
y  C x   C1 - C2  X  F 1  F 2  U  d


~
1
~
y  C sI - A   A1  A2  A1 B  B1  B2  F 1  F 2   C1  C 2  A1 B U d
Prof. Porfírio Cabaleiro Cortizo
15
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
iL
Durante t on:

x  A1 x  B1u
vO
vc
y  C1 x  F1u
 1
Rrc


r


 il   L  l R  rc
 
R
 vc 

 C  R  rc 

 Rrc
vo  
 R  rc
Prof. Porfírio Cabaleiro Cortizo



R 

R  rc 

R

L R  rc  

1


C ( R  rc ) 

1
 il   
    L e
 vc 
0 
 il 
 
vc 
16
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
iL
Durante t off :

x  A2 x  B2 u
vO
vc
y  C 2 x  F2 u
 1
Rrc


r


 il   L  l R  rc
 
R
vc 

 C  R  rc 

 Rrc
vo  
 R  rc
Prof. Porfírio Cabaleiro Cortizo



R 

R  rc 

R

L R  rc  

1


C ( R  rc ) 

 il 
 
 vc 
 il 
 
 vc 
17
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
 1
Rrc
   r l 
L
R  rc

A1  A2  A 

R

 C  R  rc 



1
B1   L 
 
0 
d 
B   L
 
0 
B2  0
 Rrc
C1  C 2  C  
 R  rc
Prof. Porfírio Cabaleiro Cortizo

R


L R  rc  

1


C ( R  rc ) 
R 

R  rc 
18
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
Termo c.c.


Vo   CA 1 B E
Vo 
Prof. Porfírio Cabaleiro Cortizo
R
DE
R  rl
19
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
Termo c.a.: Influência das variações do ciclo de trabalho


~
1
~
vo  C sI - A  B1 Ed
1
z 
Crc
R  rl
 
LC  R  rc 
2
o

s  ~
E 1   k b d
z 

~
vo 
s
s2
1
 2
Q.o o
Prof. Porfírio Cabaleiro Cortizo
Q
kb 
o
rl
1
Rrc


L C  R  rc  L R  rc 
R
R  rl
20
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
Termo c.a.: Influência das variações da tensão de entrada


1
~


vo  C sI - A B ~
e
1
z 
Crc
R  rl
 
LC  R  rc 
2
o

s  ~
D 1   kb e
z 

~
vo 
s
s2
1
 2
Q .o o
Prof. Porfírio Cabaleiro Cortizo
Q
kb 
o
rl
1
Rrc


L C  R  rc  L R  rc 
R
R  rl
21
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck em MCC
Projetando o conversor para a seguinte condição:
Emax = 60V
Emin = 40V
Vo = 24V
L = 560mH
rL = 0,1W
C = 220mF
rC = 0,1W
Rmax = 600W
Rmin = 6W
Prof. Porfírio Cabaleiro Cortizo
22
Fontes de alimentação c.c.-c.a
Exemplo: Conversor buck e a malha de controle da tensão de saída
MODO TENSÃO
Vo
E
Carga
“Buck”
Realimentação
PWM
Ref.
Regulador
Prof. Porfírio Cabaleiro Cortizo
23
Fontes de alimentação c.c.-c.a
Exemplo: Diagrama de blocos do Conversor e da malha de controle
Tensão de
entrada
Tensão
de ref.
Regulador
PWM
Carga
Etapa de
potência
Tensão de
saída
-
Realimentação
Prof. Porfírio Cabaleiro Cortizo
24
Fontes de alimentação c.c.-c.a
Modelamento do bloco amostrador da tensão de saída
vr0
R1 +
+
R2
-
Equação (a vazio):
vO
vr0 =
Rede de realimentação
-
R1 + R2
vO
Linearização:
(R1·R2)/ (R1 + R2)
+
R2
+
vr0 =
-
R2
R1 + R2
^
vr0 =
vO
R2
R1 + R2
^
vO
Circuito equivalente
Prof. Porfírio Cabaleiro Cortizo
25
Fontes de alimentação c.c.-c.a
Modelamento do bloco Modulador por Largura de Pulso
VP
PWM
d
vgs
vd
+
+
-
-
vd
VV
vgs
Equação:
d=
VPV
tC
T
vd - VV
VPV
Prof. Porfírio Cabaleiro Cortizo
tC = d·T
Linearização:
d/vd = 1/VPV
1 ^
^
vd
d=
VPV
26
Fontes de alimentação c.c.-c.a
Modelamento do bloco regulador e amostrador
Z1
Linearização:
vd =
Z1 + Z2
Z1
Prof. Porfírio Cabaleiro Cortizo
vREF -
Z2
Z1
vro
^
vd = -
Z2
R2 ^
vO
·
Z1 R1 + R227
Fontes de alimentação c.c.-c.a
^
r
^
vREF=0
Z2
^
vd
Z1
-
1
VPV
^
vO
Etapa de
potência
^
d
?
R2
^
vr0
R1 + R2
^
r
R2
^
vr0 -Z2 ^
vd
R1 + R 2
Z1
^
vO
Prof. Porfírio Cabaleiro Cortizo
^
e
1
VPV
^
d
Etapa de
potencia
^
e
^
vO
?
28
Fontes de alimentação c.c.-c.a
Conclusão do caso “sem isolamento galvânico”
^
e
^
r
R2
^
vr0 -Z2 ^
vd
R1 + R 2
Z1
^
vO
1
VPV
^
d
Etapa de
potência
^
vO
?
Z1 = (R1·R2)/(R1+R2)
^
d=
- Z2 ·R2
Vpv·Z1· (R1+R2)
Prof. Porfírio Cabaleiro Cortizo
^
vO
29
Fontes de alimentação c.c.-c.a
Diagrama de blocos completo para
conversores sem isolamento galvânico
^
vO
Prof. Porfírio Cabaleiro Cortizo
R2
-Z2
R1 + R2
Z’1
^
r
Ior
^
e
Gvg
1
VPV
^
d
+ +
Gvd
+
^
vO
30
Fontes de alimentação c.c.-c.a
Prof. Porfírio Cabaleiro Cortizo
31