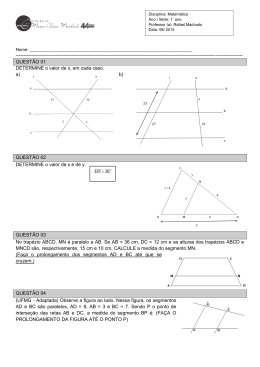
Geometria I
Lista de Exercícios 8
1)
Na gura abaixo, ABCD é um retângulo, M é o ponto médio de CD
e ∆AM B é um triângulo equilátero. Sabendo que AB = 15, calcule o
comprimento AP .
2)
Na gura abaixo, calcule o perímetro do triângulo ∆ARS sabendo que
←
→ ←→
AB = 15 e AC = 18, também que RS//BC e BQ e CQ estão, respectivamente, sobre as bissetrizes dos ângulos ∠ABC e ∠ACB .
3)
Na gura abaixo, o triângulo ∆ABC é retângulo, com ângulo reto em B ,
←→ ←→
P é o ponto médio de AC e P Q//BC , calcule P O.
4)
Na gura abaixo, ABCD é um quadrado e ∆BCE é um triângulo equilátero. Determine a medida do ângulo AÊD
Calcule a área de um triângulo equilátero de lado l.
Calcule a área de um hexágono regular de lado l.
Determine os raios da circunferência inscrita e da circunferência circunscrita a um quadrado de lado l.
8) Determine os raios da circunferência inscrita e da circunferência circunscrita a um triângulo equilátero de lado l.
5)
6)
7)
1
2
Determine os raios da circunferência inscrita e da circunferência circunscrita a um hexágono regular de lado l.
10) Verique que o centro da circunferência inscrita e da circunferência circunscrita de um polígono regular coincidem.
11) Mostre que a área de um polígono regular é igual ao produto do seu
semiperímetro (metade do perímetro) pela medida do apótema (segmento
perpendicular ao lado que sai do centro da circunferência inscrita).
12) Na gura abaixo, ABCD é um trapézio retângulo e P é o ponto médio
de AD. Calcule a área do quadrilátero ABQP , sabendo que P Q ⊥ BC ,
AB = 9, BC = 8 e CD = 7.
9)
13)
Mostre que, dado um quadrilátero convexo qualquer, o quadrilátero formado pelos pontos médios dos lados é um paralelogramo com exatamente
metade da área do quadrilátero original.