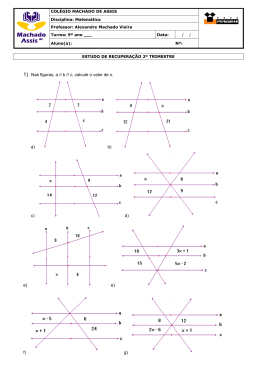
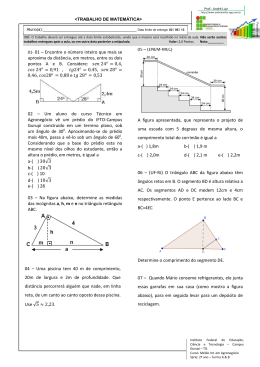
CIANSP - COLÉGIO NOSSA SENHOR A DA PIEDADE
R u a M o n s e n h o r D o m i n go s P i n h ei r o , 3 5 – C a l a f a t e / B H
F o n e : ( 3 1 ) 3 3 3 4 6 9 1 3 - c o o r d en a c a o @ c o l e g i o pi e da d e. c o m . b r
76 Anos Educando para a Vida
DISCIPLINA MATEMÁTICA
PROFESSORA: DENIZE
TRABALHO DE
RECUPERAÇÃO
DATA DE ENTREGA:17/12/15
ALUNO(A):
TURMA:2º ANO
ENSINO: MÉDIO
VALOR:20 PONTOS
NOTA:
Nº:
INTRODUÇÃO:
Este roteiro tem como objetivo orientá-lo nos estudos de recuperação. Ele consta de informações
gerais, uma lista de conteúdos contendo temas significativos e habilidades básicas para a continuidade
dos seus estudos, algumas orientações de estudo específicas da disciplina e uma atividade a ser
realizada em casa durante o período de preparação para a prova. Para que você tenha um bom
desempenho nesta recuperação, recomendamos um estudo diário e regular e a realização completa e
precisa da atividade indicada neste roteiro. É muito importante, neste processo, a sua disposição para
recuperar seu desempenho acadêmico, o que pressupõe esforço, disciplina, organização e
responsabilidade.
ORIENTAÇÕES GERAIS
1. A seleção do conteúdo para o estudo de recuperação foi feita considerando a sua importância
dentro da matéria e seu pré-requisito.
2. Conteúdos a serem estudados:




Geometria Espacial e Plana
Poliedros
Corpos Redondos
Análise Combinatória
3. A atividade deverá ser entregue no dia da avaliação, em folha de papel almaço. Valor 20,00
pontos.
1. Das afirmações:
I. Duas retas coplanares são concorrentes;
II. Duas retas que não têm ponto em comum são reversas;
III. Dadas duas retas reversas, existem dois, e apenas dois, planos paralelos, cada um contendo uma
das retas;
IV. Os pontos médios dos lados de um quadrilátero reverso definem um paralelogramo,
é (são) verdadeira(s) apenas
a) III.
b) I e III.
c) II e III.
d) III e IV.
e) I e II e IV.
2. (Ufrn 2002) Na cadeira representada na figura a seguir, o encosto é perpendicular ao assento e este
é paralelo ao chão.
Sendo assim,
a) Os planos EFN e FGJ são paralelos.
b) HG é um segmento de reta comum aos planos EFN e EFH.
c) Os planos HIJ e EGN são paralelos.
d) EF é um segmento de reta comum aos planos EFN e EHG.
3.. (Fuvest 2013) No paralelepípedo reto retângulo ABCDEFGH da figura, tem-se AB  2, AD  3 e
AE  4.
a) Qual é a área do triângulo ABD?
b) Qual é o volume do tetraedro ABDE?
c) Qual é a área do triângulo BDE?
d) Sendo Q o ponto do triângulo BDE mais próximo do ponto A, quanto vale AQ?
4. Num quadrado de lado 10 cm está circunscrita uma circunferência. Determine o raio, o comprimento
e a área da circunferência.
5.O lado de um triângulo eqüilátero inscrito numa circunferência mede 2 cm. Determine a medida da
altura do triângulo, do raio da circunferência, da área do triângulo e da área da circunferência.
6.Um círculo de 5 cm de raio está inscrito em um hexágono regular. Determine o perímetro e a área do
hexágono.
7. O apótema do quadrado inscrito numa circunferência é igual a 2 cm. Determine a área do hexágono
regular inscrito nessa mesma circunferência.
8. Determine a área das figuras abaixo:
a)
b)
c)
d)
10. No quadrado ABCD de lado 2, traçam-se dois arcos com centro nos vértices A e C e raio igual ao
lado do quadrado. Determine área delimitada por estes dois arcos.
11. (Cefet-CE) Calcule a área hachurada da figura, sabendo-se que "O" é o centro das circunferências e
OA = 4 cm e AB = 5 cm.
12. Na circunferência da figura de centro 0 e raio igual a 9 m, sabe-se que a tangente PB  2PA . A
distância do ponto P à circunferência é:
13. (Ufpe 2012) Um joalheiro fabricou um pingente maciço de prata banhado a ouro, no formato de
tetraedro regular com 1cm de aresta. O custo com material para confeccionar o pingente foi R$11,25
(R$3,75 em prata e R$7,50 em ouro). Quanto o joalheiro gastará com material para confeccionar outro
pingente do mesmo tipo com aresta 2 cm? Considere que a espessura do banho de ouro permanece
constante nos pingentes.
14. (Ufpe 2011) Uma pirâmide hexagonal regular tem a medida da área da base igual à metade da área
lateral. Se a altura da pirâmide mede 6 cm, assinale o inteiro mais próximo do volume da pirâmide, em
cm3 . Dado: use a aproximação:
3  1,73 .
15. (Ufg 2013) Um cone circular reto de madeira, homogêneo, com 20 cm de altura e 20 cm de
diâmetro da base, flutua livremente na água parada em um recipiente, de maneira que o eixo do cone
fica vertical e o vértice aponta para baixo, como representado na figura a seguir.
Denotando-se por h a profundidade do vértice do cone, relativa à superfície da água, por r o raio do
círculo formado pelo contato da superfície da água com o cone e sabendo-se que as densidades da
água e da madeira são 1,0 g/cm3 e 0,6 g/cm3, respectivamente, os valores de r e h, em centímetros,
são, aproximadamente:
Dados:
3
3  1,44,
3
5  1,71.
a) 5,8 e 11,6 b) 8,2 e 18,0
c) 8,4 e 16,8
d) 8,9 e 15,0
e) 9,0 e 18,0
16. (Uece 2014) Um poliedro convexo tem 32 faces, sendo 20 hexágonos e 12 pentágonos.Determine
O número de vértices deste polígono
17.(Uerj 2016) Dois dados, com doze faces pentagonais cada um, têm a forma de dodecaedros
regulares. Se os dodecaedros estão justapostos por uma de suas faces, que coincidem perfeitamente,
formam um poliedro côncavo, conforme ilustra a figura.
18.. Considere o número de vértices V, de faces F e de arestas A desse poliedro côncavo.
A soma V  F  A é igual a:
19.. Determine a área de uma praça circular cuja circunferência mede 376,80 m.
20. Um setor circular tem área igual a 45,40 m2 e o ângulo dele é de 36º. Qual é a medida do seu raio
21. (Epcar-SP) De um ponto P, traça-se uma tangente e uma secante a um círculo. Se o segmento PT
de tangente mede 8 m e o segmento PB da secante mede 16 m, qual deve ser, em metros quadrados,
a área do círculo, se a secante contém o diâmetro do mesmo?
22. A área da região pintada vale, aproximadamente:
3 cm

5 cm
23. A área da região pintada na figura abaixo é:
24. (UFS-SE) A área, em centímetros quadrados, do triângulo representado na figura abaixo é:
5 cm
30º
8 cm
25. Uma lata de refrigerante tem a forma de um cilindro, com 8cm de diâmetro e 11 cm de altura.
Quantos ml (mililitros) de refrigerante cabem nessa lata? (considere PI = 3,14).
26. Calcule o volume e a medida da geratriz de um cone onde o raio da base mede 9 cm e a altura
mede 12 cm. (considere PI = 3,14).
27. Em um prisma regular triangular, cada aresta lateral mede 10 cm e cada aresta da base mede 6 cm.
Calcular desse Prisma:
a) a área de uma face lateral.
b) a área de uma base.
c) a área lateral.
d) a área total.
28. Em uma piscina regular hexagonal cada aresta lateral mede 8 dm e cada aresta da base mede 4
dm. Calcule, desses prisma:
a) a área de cada face lateral;
b) a área de uma base;
c) a área lateral;
d) a área total;
29. O comprimento EA, a largura EH e a altura EF do paralelepípedo reto-retângulo representado ao
lado são 12 cm, 3 cm e 4cm, respectivamente:
Calcule:
a) a medida de uma diagonal da face EFGH;
b) a medida de uma diagonal do paralelepípedo;
c) a área total do paralelepípedo;
d) o volume do paralelepípedo;
30. Uma moeda é lançada 3 vezes. Qual o número de sequências possíveis de cara e coroa?
31. A turma M.26 tem 19 alunos. Um deles será escolhido para ser representante de turma e outro para
vice. Qual é o número de possíveis disposições das pessoas nas vagas?
32. De quantas maneiras podemos responder a 10 perguntas de um questionário, cujas respostas para
cada pergunta são: sim ou não?
33. Chamamos de anagrama a um agrupamento de letras formado a partir de um conjunto de letras,
tendo ou não sentido a palavra formada por esse agrupamento. Desta forma determine quantos são os
anagramas formados com as letras da sigla UFMG.
34. Quantos anagramas podemos fazer com a palavra ASTRIDE, que:
a) começam com vogal;
b) T e R aparecem juntas;
c) começam com DE;
35. Simplifique as expressões abaixo:
a)
10!
8!
e)
(n  1)!
n
b)
12 !
9 !.3!
f)
m!
(m  2)!
c)
m!
(m  1)!
g)
n!
(n  p)!
d)
( n  1)!
( n  1)!
36.. Com oito pessoas que sabem dirigir, de quantas maneiras distintas conseguimos
colocar 5 delas em um fusca?
37.Um banco pede que cada cliente crie uma senha para se utilizar de seu sistema
informatizado. Como essa senha deve ter 5 algarismos distintos, quantos são as possíveis
senhas? E se pudesse haver repetição?
38. Com um grupo de 10 homens e 10 mulheres, quantas comissões de 5 pessoas podemos formar se
em cada uma deve haver 3 homens e 2 mulheres?
39. Um químico dispõe de 9 substâncias para realizar três experimentos (A, B e C). De quantos modos
poderá fazer os experimentos, colocando 4 substâncias no experimento A, 3 substâncias no
experimento B e 2 substâncias no experimento C?
40. Sobre duas retas paralelas marcam-se respectivamente, 7 pontos e 9 pontos. Quantos triângulos
podemos determinar com estes 16 pontos?
41. Quantas diagonais tem um octógono?
42. Sabendo-se que
C8, p  2
C8, p  1
 2 , determine o valor de p.
43. A equação A n , 2 + A n 1, 2 =18:
a) possui infinitas raízes distintas
b) possui duas raízes distintas
c) possui uma única raiz
d) não possui raiz