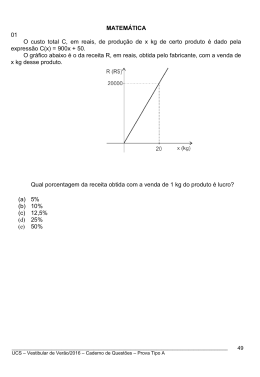
MATEMÁTICA
01
Por meio da expressão – 3p(p – 50), na qual p indica o preço de venda por unidade, é possível determinar a receita
total mensal que um empreendedor individual obtém com a venda do seu produto.
Analise quanto à veracidade (V) ou falsidade (F) as proposições abaixo, referentes ao produto mencionado.
( )
( )
( )
O preço ótimo de venda, isto é, o preço que gera receita total mensal máxima, é R$ 50,00 por unidade.
A receita mensal máxima é R$ 5 625,00.
Vendendo a unidade do produto por R$ 10,00 ou por R$ 40,00, a receita mensal total será a mesma.
Assinale a alternativa que preenche corretamente os parênteses, de cima para baixo.
a)
b)
c)
d)
e)
V–V–V
V–F–F
F–V–F
F–F–V
F–V–V
02
Segundo alguns estudos, a temperatura média da superfície da Terra, que é tida como 15 °C aproximadamente, vem
aumentando, enquanto outros estudiosos argumentam que sequer é possível pensar nessa temperatura média, tendo em
vista os diferentes extremos de temperaturas nas variadas regiões do Planeta.
Alguns cientistas, em seus estudos, consideraram que, em uma determinada região, a temperatura média anual em
1950 era 9,5 °C e, usando um modelo matemático cujo gráfico é uma reta, deduziram que, no ano de 2000, ela era
10,5 °C.
Usando o modelo matemático mencionado, a projeção que os cientistas referidos fazem para a temperatura média da
superfície terrestre na região, em 2020, é de
a) 12,94 °C.
b)
c)
d)
e)
10,90 °C.
11,85 °C.
10,20 °C.
15,00 °C.
03
Em geral, materiais radioativos se desintegram (se transmutam) espontaneamente com o passar do tempo, por meio
da emissão de radiação. Como a desintegração se dá de forma proporcional à massa remanescente do material, o
modelo matemático para o cálculo da quantidade em função do tempo é um modelo exponencial. O tempo necessário
para que a quantidade de massa se reduza à metade é chamado, nesse caso, de meia-vida do elemento.
Se considerarmos que a meia-vida do césio-137 é de 30 anos e que 100 mg desse elemento tenham sido liberados
ℓn 2
para o meio ambiente, a expressão que permite calcular a quantidade que restará t anos após a liberação, é 100 − 30 t
e
. De acordo com essa expressão, usando ℓn2 = 0,7 e ℓn5 = 1,61, qual é o tempo mínimo, em anos, para que a
quantidade liberada para o meio ambiente seja reduzida a 5% da quantidade inicial?
a)
b)
c)
d)
e)
125
127
129
135
134
_______________________________________________
UCS – Vestibular de Inverno 2011 – Caderno de Questões
29
04
Um enfeite maciço tinha a forma de pirâmide quadrangular regular, de aresta da base igual a 10 cm e altura 16 cm.
Cortou-se esse enfeite com uma lâmina plana, interceptando-o a uma altura correspondente à metade da altura da
pirâmide original, de forma a determinar uma secção plana transversal paralela à base. (Veja a figura abaixo.)
A relação entre os volume V1 e V e a relação entre as áreas das bases B1 e B da pirâmide formada e da pirâmide
original, são, respectivamente,
1
V
2
1
b) V1 = V
2
1
c) V1 = V
8
1
d) V1 = V
8
e) V1 = V – 8
a) V1 =
1
B
2
1
B1 = B
4
1
B1 = B
4
1
B1 = B
2
B1 = B – 4
e B1 =
e
e
e
e
05
Uma roleta de 50 cm de raio está fixada por um parafuso em seu centro, que se encontra a uma altura de 1,5 m.
Girando a roleta no sentido horário, seu ponto inicial, posicionado na horizontal à direita, foi deslocado para uma altura de
1,75 m à esquerda.
Se a opção tivesse sido girar a roleta no sentido anti-horário, qual teria sido o ângulo de rotação para que o ponto
inicial fosse deslocado para a mesma posição?
a)
b)
c)
d)
e)
π
rad
6
5π
rad
6
2π
rad
3
3π
rad
4
π
rad
3
06
A avaliação do número de pessoas em eventos públicos costuma ser feita considerando a concentração de um número
máximo de quatro pessoas por m2.
Segundo esse critério, em uma área ao ar livre, com a forma da figura abaixo, em que A, B, e C são quadrados e o
perímetros de A e B são, respectivamente, 16 m e 40 m, e somente a região D é destinada ao público, o número máximo
de pessoas que poderão participar do evento é
a) 2560.
b)
c)
d)
e)
4656.
3248.
4800.
3456.
_______________________________________________
UCS – Vestibular de Inverno 2011 – Caderno de Questões
30
07
Suponha que um produto custasse R$ 2 000,00 em 01 de janeiro deste ano. Quanto ele custaria, em reais, em 01 de
julho deste ano, na hipótese de uma inflação de 2% ao mês, desde janeiro?
a)
b)
c)
d)
e)
2 000 (1,02)6
2 000 (1,02)7
2 000 (1,20)6
2 000 (1,20)7
2 000 (0,02)7
08
Suponha que um lojista, na semana anterior ao início do “Liquida Caxias”, tenha elevado o preço de suas mercadorias
em 40% e divulgado, no início da campanha, uma remarcação com desconto de 50% em todos os preços.
O desconto realmente concedido em relação aos preços originais foi de
a)
b)
c)
d)
e)
10%.
20%.
25%.
30%.
35%.
09
Uma partícula move-se ao longo de uma trajetória circular de raio 1,0 cm. O movimento é referenciado por um sistema
de eixos cartesianos, cuja origem coincide com o centro do círculo. Quando a partícula passa pelo ponto (x,y) do primeiro
quadrante, em que x = 0,6, o valor de y é
a) 0,4.
b) 0,3.
c) 0,6.
d) 0,2.
e) 0,8.
10
Para uma feira de dois dias, da qual a UCS irá participar com um estande, foi escolhido um aluno de cada uma das oito
diferentes cidades em que a UCS mantém campus ou núcleo. Está previsto que no estande irão trabalhar no primeiro dia
quatro alunos e no segundo dia outros quatro.
De quantas maneiras pode ser organizada a escala?
a)
b)
c)
d)
e)
8
12
24
64
70
_______________________________________________
UCS – Vestibular de Inverno 2011 – Caderno de Questões
31