MATEMÁTICA
49
Um terreno comprado por R$ 30 000,00 valorizou de tal maneira, que seu valor no mercado
imobiliário 2 anos após sua compra era de R$ 50 000,00, e 5 anos após a compra era de
R$ 68 000,00.
Admitindo que em cada um dos períodos, de 0 a 2 anos e de 2 a 5 anos após a compra, os
acréscimos no valor do terreno tenham sido proporcionais aos acréscimos no tempo (em meses)
decorrido após a compra, o valor do terreno 2 anos e 3 meses após a sua compra era igual a
a) R$ 51 500,00.
b) R$ 52 000,00.
c) R$ 52 400,00.
d) R$ 52 500,00.
e) R$ 53 000,00.
50
Uma tela retangular, como a representada pela figura abaixo, está fixa em uma
parede. Deseja-se pintar os 6 retângulos dessa tela com cores distintas.
Dispondo de 9 cores diferentes, o número total de possibilidades de pintar a tela, sempre
mantendo cores distintas nos retângulos, é igual a
a)
84.
b)
720.
c)
504.
d)
54.
e)
60 480.
----------------------------------------------------
UCS – Vestibular de Verão 2005 – Prova 2 – A
3
51
Uma liga de ouro de 18 quilates é assim considerada se do total das partes iguais que ela
contém, 18 forem de ouro puro e as 6 restantes de um metal subsidiário.
A quantidade de ouro puro que há em uma jóia de 50 g de uma liga de ouro de 18 quilates
corresponde a __________ da liga.
Assinale a alternativa que completa corretamente a lacuna acima.
a)
18%
b)
30%
c)
37,5%
d)
75%
e)
90%
52
Uma indústria fabrica três tipos de produto: A, B e C.
Estimados para o ano de 2005, os custos de produção de uma unidade de cada um dos
produtos A, B e C, com matéria-prima, pessoal e despesas gerais são dados, em reais,
respectivamente, pelas 1ª, 2ª e 3ª linhas da matriz M.
Nas 1ª, 2ª e 3ª linhas da matriz P consta, respectivamente, o número de unidades dos
produtos A, B e C a serem fabricadas em cada um dos três quadrimestres de 2005.
2 3 1,50 


M = 5 4 2,50 
1 2 1,50 
4000 4500 4500 


P = 2000 2600 2400 
5000 6200 6000 
O custo com pessoal para cada quadrimestre, que a indústria estima para o ano de 2005, é
dado
a)
b)
c)
d)
e)
pela soma dos elementos da 2ª linha da matriz-produto PM.
pelos elementos da 2ª linha da matriz-produto PM.
pelos elementos da 2ª linha da matriz-produto MP.
pelos elementos da 2ª linha da matriz-soma M+P.
pelos elementos da 2ª coluna da matriz-produto MP.
----------------------------------------------------
UCS – Vestibular de Verão 2005 – Prova 2 – A
4
53
Planeja-se construir um tanque cuja forma, constituída de
S E M I-E S F E R A
um cilindro circular reto e de uma semi-esfera, está representada
geometricamente pela figura ao lado.
A capacidade total do tanque deverá ser de 1 008
π metros
cúbicos. Se a medida interna do raio da base do tanque for igual
C IL IN D R O
a 6 metros, a altura interna total do tanque deverá ser igual a
a)
30 m.
b)
24 m.
c)
12 m.
d)
18 m.
e)
15 m.
54
A quantia de R$ 16 500,00 foi investida em três contas C1, C2 e C 3. Ao final do primeiro ano
de aplicação, o lucro obtido em cada uma das contas foi de 5%, 8% e 10%, respectivamente.
A quantia que rendeu 5% era igual à quantia que rendeu 8% mais o dobro da quantia que
rendeu 10%.
Se, ao término desse ano, o valor total em juros sobre o investimento foi de R$ 1 085,00, o
valor investido em cada uma das contas C1, C2 e C 3 terá sido, respectivamente, de
a)
R$ 9 000,00, R$ 4 000,00 e R$ 2 500,00.
b)
R$ 9 500,00, R$ 4 500,00 e R$ 2 500,00.
c)
R$ 8 500,00, R$ 4 500,00 e R$ 3 500,00.
d)
R$ 6 000,00, R$ 6 000,00 e R$ 4 500,00.
e)
R$ 6 000,00, R$ 5 500,00 e R$ 5 000,00.
----------------------------------------------------
UCS – Vestibular de Verão 2005 – Prova 2 – A
5
55
Um estudante, observando o aumento do número de bactérias em certa cultura, construiu a
tabela a seguir:
Número de minutos
0
20
Número de bactérias
6 000
9 000
Com base nesses dados e com a finalidade de expressar o número de bactérias da cultura
kt
em relação ao tempo, o estudante usou uma função exponencial da forma Q(t) = Ae , em que
“e” é o número real tal que "Q e = 1.
Utilizando "Q 3 = 1,1 e "Q 2 = 0,7, ele obteve para Q(t) a expressão
a)
6 000 e
0,02 t
b)
9 000 e
- 0,02 t
c)
6 000 e
0,4 t
.
d)
3 000 e
0,4 t
.
e)
9 000 e
0,2 t
.
.
.
56
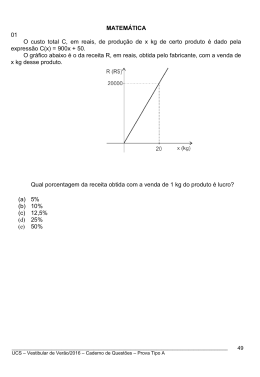
O lucro obtido pela produção, comercialização e venda de x unidades de uma determinada
mercadoria, denotado por L(x), é igual a R(x) - C(x), em que R(x) representa a receita obtida
com a venda e C(x) representa os custos de produção e venda de x unidades da mercadoria.
2
Se R(x) = 900x - 10x e C(x) = 500 + 300x, para obter lucro máximo, devem ser vendidas
__________ unidades da mercadoria.
Assinale a alternativa que preenche corretamente a lacuna acima.
a)
b)
c)
d)
e)
20
30
15
18
24
----------------------------------------------------
UCS – Vestibular de Verão 2005 – Prova 2 – A
6
57
Uma pessoa decidiu jogar na Mega-Sena por 10 sorteios seguidos apostando em cada um
deles o dobro do que apostou no sorteio anterior.
Começando com uma aposta de R$ 1,50, ao final dos 10 jogos, o apostador terá gasto um
total de
a)
R$ 1 024,00.
b)
R$ 2 536,00.
c)
R$ 2 540,00.
d)
R$ 768,00.
e)
R$ 1 534,50.
58
Um atleta está correndo em uma pista que tem forma de coroa circular, fazendo uma
trajetória também circular de raio igual a 300 metros e cujo centro é o mesmo das
circunferências que delimitam a pista.
O ângulo central que subentende um percurso de 1,8 km realizado pelo atleta é de
a)
4 radianos, sendo que ele percorreu mais que meia volta, porém menos que ¾ de uma volta
completa.
b)
4 radianos, sendo que ele percorreu mais que ¾ de uma volta completa.
c)
2 radianos, sendo que ele percorreu mais que ¼ de uma volta completa, porém menos do
que meia volta.
d)
6 radianos, sendo que ele percorreu menos que ¾ de uma volta completa.
e)
6 radianos, sendo que ele percorreu mais que ¾ de uma volta completa.
----------------------------------------------------
UCS – Vestibular de Verão 2005 – Prova 2 – A
7
59
As vendas mensais de um determinado produto estão sujeitas à variação sazonal. A
equação v(x) = 500 + 300 sen(2πx/12), na qual x
∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} e indica
os meses do ano de janeiro a dezembro, fornece um valor aproximado do total de vendas por
mês.
Segundo essa equação, as vendas do produto atingem seu ponto máximo no mês
a)
9.
b)
4.
c)
6.
d)
3.
e)
12.
60
Deseja-se recortar de uma placa de alumínio uma arruela que tenha a forma da coroa
2
2
circular determinada pela intersecção do conjunto de pontos (x, y) do plano, tais que x + y ≤ 9,
2
2
com o conjunto de pontos (x, y) do plano, tais que x + y ≥ 1.
Sendo a unidade de medida o centímetro, quantos centímetros quadrados terá a arruela
fabricada?
a)
6 π.
b)
2 π.
c)
8 π.
d)
9 π.
e)
10 π.
----------------------------------------------------
UCS – Vestibular de Verão 2005 – Prova 2 – A
8