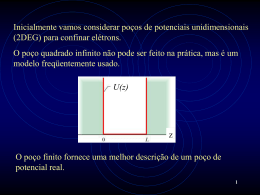
Aula-8 Fótons e ondas de matéria III Curso de Física Geral F-428 A equação de Schrödinger • Embora tenha obtido alguns sucessos notáveis, a velha teoria quântica (1900 ~ 1920) tinha sérios defeitos. Era uma mistura arbitrária de física clássica com novos postulados, alheios e contraditórios à própria física clássica. Erwin Schrödinger • Em 1926, Schrödinger foi convidado a dar um seminário na universidade de Zurich sobre a teoria de de Broglie. Durante o seminário um dos ouvintes perguntou como ele podia falar abertamente sobre uma onda associada ao elétron, se não havia nenhuma equação de onda ! Alguns meses depois, Schrödinger apresentou a equação de onda, dando início a mecânica quântica moderna. A equação de Schrödinger “ Nossa mecânica clássica talvez seja completamente análoga à óptica geométrica e por isso falha, estando em desacordo com a realidade… Portanto é preciso estabelecer uma mecânica ondulatória…” - Schrödinger, 1926. A equação de Schrödinger não pode ser deduzida, assim como não podem ser deduzidas as equações da dinâmica de Newton. Ela só pode ser postulada. A forma escolhida deveria incorporar o sucesso das teorias anteriores. Fatalmente, ela também levaria a novas previsões (e interpretações) que poderiam ser testadas. A equação de Schrödinger • Os fenômenos ondulatórios, independentemente da sua origem, têm a sua evolução temporal descrita por equações de onda do tipo: 1 F (r , t ) 2 F (r , t ) 0 2 2 c t 2 onde F (r , t ) é a variável dinâmica de interesse; por exemplo: o campo elétrico ou o campo magnético da radiação EM. • Se quisermos investigar a evolução temporal da densidade de probabilidade (r , t ) | (r , t ) |2 , devemos estudar como (r , t ) varia no tempo. No que segue, vamos fazer essa análise apenas para partículas massivas! A equação de Schrödinger Em geral podemos dizer que para uma onda plana temos: (r , t ) 0 exp i(k r t ) Derivando (r , t ) com relação a t : (r , t ) i (r , t ) t Tomando o gradiente de (r , t ) e depois a sua divergência ( r , t ) ik ( r , t ) 2 2 [ ( r , t )] ( r , t ) k ( r , t ) A equação de Schrödinger Então: e (r , t ) i (r , t ) E (r , t ) t 2 2 2k 2 p2 (r , t) (r , t ) ( r , t ) E ( r , t ) 2m 2m 2m Equação de Schrödinger da partícula livre (E = Ek ; V = 0) : (r , t ) 2 2 i (r , t ) t 2m A equação de Schrödinger Mas, no caso geral , não – relativístico: p2 E V (r ) 2m p2 E (r , t ) (r , t ) V (r ) (r , t ) 2m Equação de Schrödinger (Postulada!) ( r , t ) 2 2 i ( r , t ) V ( r ) ( r , t ) t 2m A equação de Schrödinger Onda estacionária: (r , t ) (r ) exp(it ) substituindo na Eq. de Schrödinger: (r , t ) 2 2 i (r , t ) V (r ) (r , t ) t 2m obtemos: 2 2 (r ) E (r ) (r ) V (r ) (r ) 2m Equação de Schrödinger independente do tempo. A partícula livre em 1-D Para encontrar a solução geral de: ( x, t ) ( x, t ) i t 2m x 2 2 2 devemos resolver inicialmente: 2 d 2 ( x) E ( x) ; 2 2m dx ou: d 2 ( x ) dx 2 k ( x ) 0 ; onde 2 V (r) 0 k 2 2mE 2 A partícula livre em 1-D Solução geral: como: ( x) A exp(ikx) B exp(ikx) exp( i ) cos i sin ( x) A cos kx B sin kx ; com A' ( A B) ; B' i ( A B) ( x, t ) exp i(kx t ) ( x, t ) exp[i (kx t )] Onda propagante para a direita: Onda propagante para a esquerda: A partícula livre em 1-D Façamos: A = 0 e B = 0 ( x) 0 exp(ikx) (p/ direita) k 2 e ( x, t ) 0 exp i ( kx t ) onde ( k ) 2m 2 2 2 pois: p k 2m 2m A densidade de probabilidade para encontrar a partícula será: ( x, t ) | ( x, t ) |2 02 Constante! para - x • Ou seja, uma partícula livre pode ser encontrada em qualquer ponto sobre o eixo x, com a mesma probabilidade. 02 ( x, t ) 0 x wavemechanics-freepacket O princípio da incerteza 1 • Seja um “pacote de ondas”: ( x, t ) 2 A(k ) exp i[kx (k )t ] dk ( x x0 (t )) 2 Densidade de probab.: ( x, t ) | ( x, t ) | exp 2 2 2 [ x ( t )] 2 [ x (t )] 2 k0 x0 (t ) x0 t m 1 | ( x, t ) |2 e 4 2t 2 x(t ) x0 1 2 m (x0 ) 4 x(t ) onde: x 1 0 2k 1 2 (x(t ))2 x x0 (t ) O princípio da incerteza Propriedade da distribuição gaussiana: 1 x0 2k 1 x0 k 2 Como: x0 x(t ) x x0 p 2 Werner Heisenberg x p 2 • Relação conhecida como princípio da incerteza de Heisenberg! Não podemos determinar a posição e o momento linear de uma partícula quântica com precisão arbitrária em ambas as medidas! O princípio da incerteza • Apesar de termos mostrado essa propriedade partindo de uma distribuição gaussiana (pacote de ondas), ela é inerente à mecânica quântica. Ela se aplica sempre aos pares das chamadas variáveis incompatíveis. Essas são variáveis que não podem ser medidas simultaneamente! Em 3-D: x p x 2 y p y 2 z p z 2 Prob.1: a) Uma bola de gude, com 25 g, está numa caixa que tem 10 cm de lado. Achar a incerteza mínima no seu momento linear p e na sua velocidade v. b) Resolver o mesmo problema, para um elétron confinado numa região de comprimento de 1 Å , que é da ordem de grandeza do diâmetro de um átomo. Prob.1: m v L a) Uma bola de gude, com 25 g, está numa caixa que tem 10 cm de lado. Achar a incerteza mínima no seu momento linear p e na sua velocidade v. b) Resolver o mesmo problema, para um elétron confinado numa região de comprimento de 1 Å , que é da ordem de grandeza do diâmetro de um átomo. a) h (erg .s ) b b b b ,min x 10 cm x p x (10 cm )p x p x 2 4 (10 cm ) 6.63 10 27 (erg .s ) b ,min p x 5.28 10 29 ( g cm / s ) 40 (cm ) b p b ,min x m v b b ,min x v b) elétron num átomo: 8 x 10 cm p e p xe,min 5.28 10 20 ( g e ,min x b ,min x 6.63 10 27 (erg .s ) 2.11 10 30 (cm / s ) 40 (cm ) 25 ( g ) b ,min h (erg .s ) 9 b ,min e ,min 9 p x 10 p x ; v x 10 8 4 (10 cm ) me cm ) ; v xe,min s cm ) s 5.8 107 ( cm ) 0.019c (g) s 5.28 10 11 ( g 9.1 10 28 Prob. 2: Mostre que o número de onda angular k, de uma partícula livre não-relativística de massa m, pode ser escrito na forma abaixo, onde K é a energia cinética da partícula. 2 2m K k p k ; 2mK k 2 2 h p 2 2k 2 K 2m 2m 2mK 2 2mK k h A corrente de probabilidade Da equação de Schrödinger pode-se mostrar que: ( x, t ) d J ( x, t ) t dx onde ( x, t ) | ( x, t ) |2 e i d ( x, t ) d ( x, t ) J ( x, t ) ( x, t ) ( x, t ) 2m dx dx é a densidade de probabilidade é a corrente de probabilidade. No caso estacionário, há conservação da corrente de probabilidade! J ( x) const . O potencial degrau 1 2 E V0 0 x I) E > V0 : d 21 ( x ) 2mE 2 2 se x 0; k1 1 ( x ) 0 ; onde k1 2 2 dx 2m( E V0 ) d 2 2 ( x ) 2 2 se x 0; k 2 2 ( x ) 0 ; onde k 2 2 dx 2 O potencial degrau E > V0 : x 0 1 2 Soluções gerais: 2mE x < 0 : 1 ( x ) A exp( ik1 x ) B exp( ik1 x ) ; onde k 2 I R 2 1 x > 0 : 2 ( x ) C exp( ik 2 x ) D exp( ik 2 x ) ; onde k 22 T R mas : D = 0 , pois não há onda refletida para x > 0. 2m( E V0 ) 2 O potencial degrau d Como e são funções contínuas J ( x 0 ) J ( x 0 ) dx daí: B k1 k 2 A k1 k 2 ; amplitude de reflexão C 2k1 A k1 k 2 ; amplitude de transmissão J inc | A | v1 , J ref | B | v1 , J trans 2 2 k1 k 2 J ref B R J inc A k1 k 2 2 2 ki | C | v2 onde vi m 2 2 J trans k 2 C 4k1k 2 T J inc k1 A (k1 k 2 ) 2 R T 1 O potencial degrau 1 2 V0 E 0 x II) E < V0 : d 21 ( x ) 2 se x 0; k ; onde 1 1 ( x ) 0 2 dx 2mE k 2 d 2 2 ( x ) 2 se x 0; ; onde 2 2 ( x) 0 2 dx 2m(V0 E ) 2 2 1 2 2 O potencial degrau E < V0 : x 0 1 2 x<0: 1 ( x) A exp(ik1 x) B exp(ik1 x) ; onde x>0: 2 ( x) C exp( 2 x) D exp( 2 x) ; onde : 22 0 k12 2mE 2 2m(V0 E ) 2 O potencial degrau Como e d são funções contínuas J ( x 0 ) J ( x 0 ) dx B k1 i 2 1 2 ; amplitude de reflexão exp( 2i ) , tan A k1 i 2 k1 J inc | A | v1 , J ref 2 ki | B | v1 , onde vi m 2 2 J ref B R 1 J inc A ; T 0 2 ( x ) C exp( 2 x ) 2m(V0 E ) 1 2 wavemechanics-step Comprimento de penetração A barreira de potencial 1 2 E 3 V0 0 x L I) E > V0 : se x 0; d 21 ( x ) dx se L x 0; se x L; 2 k121 ( x ) d 2 2 ( x ) dx d 2 3 ( x ) dx 2 2 0 ; onde k 22 2 ( x ) k 32 3 ( x ) k12 0 ; onde 0 ; onde k 32 2mE 2 k 22 k12 2m( E V0 ) 2 2mE 2 A barreira de potencial E > V0 : 1 2 1 ( x ) A exp(ik1 x ) B exp( ik1 x ) ; onde 3 k12 2mE 2 2m( E V0 ) 2 ( x ) C exp(ik 2 x ) D exp( ik 2 x ) ; onde k 22 3 ( x ) E exp(ik 3 x ) F exp( ik 3 x ) ; onde k 32 k12 0 2 2mE 2 A barreira de potencial 1 2 3 V0 E 0 x L II) E < V0 : se x 0; d 21 ( x ) dx se L x 0; se x L; 2 k121 ( x ) d 2 2 ( x ) dx 2 d 2 3 ( x ) dx 2 0 ; onde k12 22 2 ( x ) 0 ; onde k 32 3 ( x ) 0 ; onde 2mE 2 22 k 32 k12 2m(V0 E ) 2 2mE 2 A barreira de potencial E < V0 : 1 2 1 ( x ) A exp(ik1 x ) B exp( ik1 x ) ; onde 3 k12 2 ( x ) C exp( 2 x ) D exp( 2 x ) ; onde 22 3 ( x ) E exp(ik 3 x ) F exp( ik 3 x ) ; onde 0 2mE 2 2m(V0 E ) 2 2mE 2 2 k 3 k1 2 A barreira de potencial d Como e são funções contínuas J ( x 0 ) J ( x 0 ) dx Coeficiente de transmissão ou taxa de tunelamento: T exp(2 L) ; onde 2m(V0 E ) 2 R 1 T 1 exp( 2 L) Coeficiente de reflexão wavemechanics-barrier Prob. 3: a) Um feixe de prótons de 5,0 eV incide em uma barreira de energia potencial de 6,0 eV de altura e 0,70 nm de largura, com uma intensidade correspondente a uma corrente elétrica de 1000 A. Quanto tempo é preciso esperar (em média) para que um próton atravesse a barreira? b) Quanto tempo é preciso esperar se o feixe contém elétrons em vez de prótons? Prob. 3: a) Um feixe de prótons de 5,0 eV incide em uma barreira de energia potencial de 6,0 eV de altura e 0,70 nm de largura, com uma intensidade correspondente a uma corrente elétrica de 1000 A. Quanto tempo é preciso esperar (em média) para que um próton atravesse a barreira? b) Quanto tempo é preciso esperar se o feixe contém elétrons em vez de prótons? a) Taxa de incidência de prótons: r = 1000(C/s) / 1,610-19(C) 6,251023 s-1 No tempo de espera t* para 1 próton tunelar: r t* T = 1 ; T exp(2 L) 8 2 m p (Vb E ) 2 (0,70 nm) 1 1 t exp 2 L exp 8 ( 938 Mev )( 6 eV 5 eV ) 1240 ( eV .nm) 6,25 10 23 ( s 1 ) r h2 * t * 3,37 10111 s 10104 anos (maior que a idade do universo ! ) b) Feixe de elétrons: me 0.511MeV / c2 te* 2 (0,70 nm) 1 exp 8 ( 0 . 511 Mev )( 6 eV 5 eV ) 23 1 6,25 10 ( s ) 1240 (eV .nm) 9 t 2.1 10 s ! * e onde: mp = 938 MeV/c2 ; me = 0.511 MeV/c2 hc = 1240 eV nm O microscópio de varredura Nobel Laureates 1986: Heinrich Rohrer , Gerd Binnig e Ernst Ruska wavemechanics-stm
Download