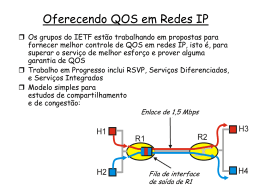
Filas M/M/1
M/M/1





É o exemplo mais simple de um PNM.
Servidor único
Processos de chegada Poisson
Tempo de serviço com distribuição
exponencial.
Política de serviço FIFO


Chegadas
de Poisson
k
Serviço
exponencial
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1
Sistema
Chegadas
fila servidor
M/M/1

Exemplo 1: seja a seguinte representação de
uma rede de comutação de pacotes
k
k
=
k=
k
: taxa de chegada dos pacotes ao nó
: taxa de saída dos pacotes para o canal
M/M/1

Segundo a solução de PNM se tem que:
 
 k   0      0  k  0

i0 
k 1
k
,
  
Por outro lado, a condição de normalização
estabelece que:    1
k
k
Portanto, se
 1 :
0  1 
M/M/1

Segundo a solução de PNM se tem que:
 
 k   0      0  k  0

i0 
k 1
k
,
  
Por outro lado, a condição de normalização
estabelece que:    1
k
k
Portanto, se
 1 :

0  1 
 k   1   k ,
    1
M/M/1
De onde:

L  E[ k ]   k k 
,
1 
k0

    1
O tempo médio de permanência no sistema,
igual ao tempo de espera mais o tempo de
serviço, se obtém pela fórmula de Little:
1
E[ k ]

T  E[ s ] 

,

1 
    1
M/M/1

Exemplo 2: considera-se agora o mesmo
sistema de filas M/M/1 do exemplo anterior,
porém a taxa de serviço é 2 .


M/M/1

O valor médio do número de pacotes no
sistema é:

E[ k ] 
,
1 
   2  1
O tempo médio de permanência no sistema é:
1
E[ k ]
2
E[ s] 

,

1 
   2  1
Gráfico comparativo
E[s]
6
5
4
M/M/1
()
3
2
M/M/1
(2
1
0
0
0,2
0,4
0,6
/2
0,8
1
E[s]= tempo de resposta normalizado
Análise de um concentrador
TERMINAL
TERMINAL
TERMINAL
CONCENTRADOR
BUFFER
TERMINAL
A ocupação média de um buffer de um
concentrador de dados pode ser calculada para
diferentes casos. Neste tipo de equipamento, os
pacotes que entram de terminais a ele
conectados são armazenados por ordem de
chegada em um buffer, e são então lidos em
FIFO sobre um enlace de saída de transmissão.
Análise de um concentrador




10 terminais estão conectados ao concentrador
Cada um gera um pacote a cada 8 segundos
(distribuição exponencial)
Pacotes têm 960 bits de comprimento em
média (distribuição exponencial)
Linha de saída com capacidade de 2400 b/s
 Ocupação
média do buffer
= E [n] = ?
 Atraso médio no sistema
= E [T] = ?
 Tempo médio de espera na fila = E [W] = ?
Análise de um concentrador

Modelo: para modelar o buffer será usada uma
fila M/M/1
Ocupação média do buffer
1
 pacotes 
  10   1.25

8
seg


Portanto:

E ( n) 
1
1 
1 960

 0.4seg
 2400

   0.5

Análise de um concentrador
Atraso médio, usando a Lei de Little:
E (T ) 
E ( n)

1
E (T ) 
 0.8seg
25
Tempo médio de espera:
E (W )  E (T ) 
E (W )  0.4seg
1

Análise de um concentrador

Cada terminal gera pacotes a cada 5 seg em
média. Encontre a ocupação média do buffer
E[n], o atraso médio E[T] e a média do tempo
de espera E[W].
Para modelar o buffer será usada uma fila
M/M/1. Ocupação média do buffer:
 pacotes 


seg


1
 0.4seg

  0 .8
E ( n)  4
Análise de um concentrador
Atraso médio, usando a Lei de Little:
E ( n)
E (T ) 

E (T )  2seg
Tempo médio de espera:
1
E (W )  E (T ) 

E (W )  1.6seg
Filas M/M/C
M/M/C





E[t] = 1/ =: tempo médio entre chegadas ao
sistema
E[x] = 1/ : tempo médio dos clientes em
serviço
u = E[x]/E[t] = / : intensidade de tráfego
C: número de servidores
A utilização de um servidor é então:
M/M/C





E[t] = 1/ =: tempo médio entre chegadas ao
sistema
E[x] = 1/ : tempo médio dos clientes em
serviço
u = E[x]/E[t] = / : intensidade de tráfego
C: número de servidores
A utilização de um servidor é então:
u



C C
M/M/2

Exemplo 3: adiciona-se outra saída, formando
um sistema de filas M/M/2



M/M/2

Para k
a taxa de serviço efetiva é 2 .
Logo, segundo a solução geral de um PNM :

k   
 2 
k 1

  0  2k  0 ,

k  1    2  1
Junto com a equação de normalização, obtémse:
0 
1 
,
1 
   2  1
M/M/2
Então,
2 1   k
k 
 ,
1 
k  1    2  1
Finalmente, a ocupação média do sistema e o
tempo médio de permanência no sistema são:
2
E[ k ] 
2 ,
1 
E[ s ] 
1

1 
2
,
   2  1
   2  1
Gráfico comparativo
E[s]6
5
M/M/1
M/M/2
4
3
2
M/M/1
2
1
0
0
0,8
0,2
1
0,4
0,6
/2
E[s]= tempo de resposta normalizado
M/M/1

Exemplo 4:




Fila M/M/1
Tempo entre chegadas = 20 [s] = 1/
Tempo de serviço = 10 [s] = 1/
Número de servidores = 1 = C

10


 0.5
C 20  1
O servidor está ocupado na metade do tempo
M/M/1

Exemplo 5:




Fila M/M/1
Tempo entre chegadas = 20 [s] = 1/
Tempo de serviço = 30 [s] = 1/
Número de servidores = 1 = C

30


 15
.
C 20  1
O sistema é inundado com chegadas (sistema
instável): pode ser resolvido com outro
servidor.
M/M/2

Exemplo anterior com dois servidores:



Tempo entre chegadas = 20 [s] = 1/
Tempo de serviço = 30 [s] = 1/
Número de servidores = 2 = C

30


 0.75
C 20  2
Os servidores estarão ocupados durante
75% do tempo
Modelos de filas aplicavéis a
centrais telefônicas
Fila M/M/
Exp ()
Exp ()
1
Exp ()
2


Parâmetros



Tempo entre chegadas ~ Exp ()
Tempo de serviço ~ Exp ()
Infinitos servidores  não existem filas

Cadeia de Markov M/M/

0


m–1
1




(m–1)

m
m
m+1
(m+1)
Equações:
n 1
i
Pn  P0  
i 0 i 1
Neste caso:

i  
,0i < 
i  i   , 0  i < 
(m+2)
De onde obtém-se que:
    n  e  
Pn 
n!
, n 0
Probabilidade de que existam n pessoas
em um sistema M/M/, com A=15 Erlangs
0.12
0.1
Pn
0.08
0.06
0.04
0.02
00
5
10
15
n
20
25
30

Observação:
Em uma fila M/M/: Pn ~ P (
Por definição: L = / 
Aplicando a Lei de Little : L = ·W
LQ = ·WQ = L – m · = L – , com:
m: número médio de servidores em uso
r: uso médio destes servidores
Então: LQ = WQ = 0,
o que está de acordo com o modelo de
infinitos servidores.
Fila M/M/m
Exp ()
Exp ()
1
Exp ()
2
Exp ()

Parâmetros

Tempo entre chegadas ~ Exp ()

Tempo de serviço ~ Exp ()

Número de servidores : m

Fator de Utilização: / m
m

Cadeia de Markov M/M/m


0

m–1
1




(m–1)

m
m

m+1
m
m
Equações:
i
Pn  P0  
i  0  i 1
n 1
Neste caso:  i  
i
i  

m  
, i 0
, 1 i  m
,
m i
Substituindo e manipulando:

m    n
, n m
 P0 
n!
Pn  
m
n
P  m   , n  m
 0
m!

P0  
 n0
m 1
m   
n!
n
m    


m! 1    
m
1

Observação:
Probabilidade de que ao chegar um pacote espere por algum
servidor livre, P(Fila):

P( Fila )   a n
n m
Como o tempo entre chegadas é distribuído
exponencialmente:
a n  Pn

Logo, a probabilidade de existir fila é dada por: P( Fila )   Pn
o que corresponde à fórmula Erlang – C :
(m   ) m

m!(1   )
P( Fila )   Pn  m 1
k
m
(
m


)
(
m


)
n m


k!
m!(1   )
k 0
n m

Exemplo

m = 8 linhas de saída.
A = 4,5 Erlangs



Problema: calcular a probabilidade de espera
Solução:
1   1
A
 0,4375
m
4,58

0,4375  8!
P( Fila )   Pn  7
k
8
4
,
5
4
,
5
n 8
 k!  0,4375  8!
k 0
P( Fila )  0,104  10,4 %

Exemplo
 PBX
com 40 ramais
 Cada ramal realiza diariamente, em média, 54
ligações
 A duração de cada ligação é, em média, de 3
minutos.

Problema 1: qual é o número de troncos de
saída necessários para uma probabilidade 5%
de que exista fila máxima?
Solução
 = 40·542460 = 1,5 ligaçõesmin
 1 = 3 minligação
 A = 1.5 · 3 = 4.5 Erlangs
 Número mínimo de troncos de saída:
m = 9 PFila = 4.61 %

Probabilidade de fila com A=4,5 Erlangs
12
10
P(Fila) %

8
6
4
2
0
8
9
10
Número de troncos (servidores)
11

Problema 2: qual é o número de troncos de
saída necessários para uma probabilidade de
0,1% de que exista fila máxima?

Solução: os parâmetros do problema se
mantém. Número mínimo de troncos de saída:
m
= 13
PFila = 0.08 %
Probabilidade de fila com A=4,5 Erlangs
0.8
P(Fila) %
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
11
12
13
Número de troncos (servidores)
14

Comparação:
 Número
mínimo de troncais de saída para :
5 %  m = 9  PF  4,61 %
 PF 0,1 %  m = 13  PF  0,08 %
 PF
 Agregaram-se
4 troncos (isto é, aumento de
44,44 %).
 Diminui-se a probabilidade de haver fila em 57,625
vezes (é dizer, diminuiu-se de 98,26 %).
Fila M/M/1/N
Exp ()
Exp ()
N N-1

3
2
Parâmetros

Tempo entre chegadas ~ Exp ()

Tempo de serviço ~ Exp ()

Número de servidores : 1

Fator de utilização: /

Cadeia de Markov M/M/1/N


0
1




N–1
2


Equações:
i
Pn  P0  
i  0  i 1
n 1
Neste caso:
i  
i 

, 0  i  N -1
, 1 i  N

N

Substituindo e manipulando :
Pn  P0   n

n 
P0     
n  0

N
 1
1 

1  N
1
Conclusão:
1 
Pn 
1  N
1
 n
, 0 n N
 Probabilidade de bloqueio M/M/1/N
PB:
probabilidade de que uma ligação que
chega encontre a fila cheia e se perca.

Fila

·PB
Da figura:
 = ·(1-PB)
Exp ()
Além do mais,  é a velocidade de
processamento  multiplicada pela fração de
tempo que o servidor trabalha o servidor,
isto é:
 = ·(1-P0)
Juntando ambas equações e manipulando:
PB  1    1  P0 
1 
PB 
1  N
1
 n
PB  PN
Aplicando a Lei de Little :
L
W
  1  PN 
Exemplo: em um PBX foram obtidas as
seguintes estatísticas:

= 15 ligaçõeshr = 0,25 ligaçõesmin
 1
= 3 minligação
Qual deve ser o tamanho do buffer para que a
probabilidade de se perder uma ligação seja
no máximo 0,1% ?


 0,75

1     N

PB 
 0,001
N 1
Solução:
1 
N  20  PB  0,08 %
buffer = 19 ligações
Probabilidade de bloqueio v/s troncos de entrada
0.35
Pb %
0.3
0.25
0.2
0.15
0.1
0.05
014
16
18
N
20
22
24
Fila M/M/N/N
Exp ()
1
Exp ()
Exp ()
2
Exp ()
N

Parâmetros




Tempo entre chegadas ~ Exp ()
Tempo de serviço ~ Exp ()
Número de servidores : N
Fator de Utilização: / N

Cadeia de Markov de M/M/N/N

0

1


Equações: 
i



N–1
2


 
N

, 0  i  N -1
 i  i   , 1 i  N
EBG:
Estado
0
0<i<N
N
V. Saída = V. Entrada
·P0  ·P1
(+i)·Pi = (i+1)·Pi+1+ ·Pi-1
N·PN = ·PN-1
Manipulando obtém-se:
 
Pi  
  Pi 
 i 
Usando:
1
N
P
i


 

 
i!
i
 P0
1
i 0
Se obtém que:
   i
Pi 
i!
N

k 0
  
k!
k
, 0 i  N
, 1 i  N
Observação: a probabilidade PN de que o
sistema se encontre cheio e que ao chegar uma
ligação esta se perca é dada pela fórmula de
perda da distribuição de Erlang:
  N !

PN  N
k
  
N

k 0
k!
As seguintes curvas são usadas para o
dimensionamento de centrais PBX:
Pb %
Probabilidade de bloqueio v/s troncos de entrada
100
90
8
0
70
60
50
40
30
20
10
0
A=30Erl
25
0
5
5
10
10
15
N
15
20
20
25
30
Dada a máxima intensidade de tráfego,
movimenta-se por uma curva, avaliando a
probabilidade de que um cliente não possa se
comunicar, para distintas quantidades de
troncos de entrada.
Probabilidade de bloqueio v/s troncos de entrada
para A = 10 Erlangs
1
0.9
0.8
Pb %
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
17
18
19
20
21
22
23
24
25
N
Supondo-se intensidade de tráfego máxima de
10 Erlangs, avalia-se as grandes diferenças
entre as probabilidades de bloqueio, usando
diferentes números de troncos de entrada.
As seguintes curvas são usadas para verificar o
dimensionamento de PBX já instaladas:
Probabilidade de bloqueio v/s intensidade de tráfego
100
90
80
Pb %
70
60
50
40
N=5
9
13
17
21
25
29
30
20
10
0
0
10
20
A [Erlangs]
30
40
50
Dada uma PBX com certo número de troncos, a
probabilidade de bloqueio é dada pela curva
correspondente, conforme seja a intensidade de
tráfego em cada momento.
Probabilidade de bloqueio v/s intensidade de tráfego
para N = 21 troncos
1.0
0.9
0.8
Pb %
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
6
7
8
9
10
11
12
13
A [Erlangs]
Observa-se que para um pequeno aumento na
intensidade de tráfego, a probabilidade de bloqueio
pode aumentar de maneira significativa.

Exemplo:
 0,4%
 N = 100 linhas
 1 = 5 minligação
 PB

Problemas:
 Determinar
a máxima intensidade de tráfego
admissível.
 Determinar a máxima taxa de chegada de
ligações para que não ocorra bloqueio.
Solução:
 Determinar
a máxima intensidade de tráfego
admissível
P100 
A 100
100!  0,004
100
Ak

k 0 k !
A = 80 Erl PB = 0,399%
Probabilidade de bloqueio v/s intensidade de tráfego
0.7
0.6
0.5
Pb %

0.4
0.3
0.2
0.1
0
78
79
80
A [Erlangs]
81
82
 Determinar
a máxima taxa de chegada de
ligações para que não ocorra bloqueio.

A

A m a x  8 0 E rl
  0 ,2
chamadas/min
 m ax  8 0  0 ,2
chamadas/min
 m ax  1 6
chamadas/min

Exemplo:
 0,5%
 A = 93,0 Erlangs
 PB

Problema:
 Determinar
o mínimo número de troncos
necessários.

Solução:
PN 
93N
N !  0,005
N
93k

k 0 k !
N = 114 Troncais
0.7
PB = 0,42%
Probabilidade de bloqueio v/s troncos
0.6
Pb %
0.5
0.4
0.3
0.2
0.1
0
111
112
113
114
N
115
116
117
Bibliografia básica
Bibliografia básica





S.M. Ross, Introduction to probability models,
Academic Press,1997.
R. Jain, The art of computer systems
performance evaluation, Wiley, 1991.
K. Trivedi, Probability and statistics with
reliability, queuing, and computer science
applications, Prentice Hall, 1982.
V. Kulkarni, Modeling and analysis of
stochastic systems, Chapman and Hall,1995.
L. Kleinrock, Queueing systems, Volume 1:
Theory, Wiley, 1975
Fim