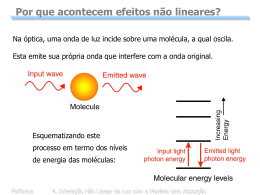
Não linearidades de Terceira-ordem :
Mistura de quatro ondas
Geração de
terceiro
harmônico
Grades induzidas
Conjugação de
Fase
Índice de refração
não-linear
Auto-focalisação
Auto- modulação
de fase
Geração de
continuo
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Geração de terceiro harmônico
THG Meio
Elevando ao cubo o campo incidente:
w
3w
E (r , t ) E exp[i(wt  kz)]  E* exp[i(wt  kz)]
E (r , t )3  E 3 exp[i(3wt  3kz )]  E *3 exp[i (3wt  3kz)]
 other+teoutros
rms termos
A geração de terceiro harmônico é mais fraca que a de segundoharmônico, soma-de-freqüência, de tal forma que se alcança o
terceiro harmônico gerando-se SHG seguido de SFG com o
fundamental, ao invés de diretamente o THG.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Geração de soma não colinear
Podemos permitir dois feixes incidentes diferentes, cujas freqüências
podem ser diferentes.
Novas possibilidades de somas de freqüências.
w
Meio
THG
Sinal #1
w w
w w
w
Sinal #2
E (r , t )3  E12 E2 exp{i[(2w1  w2 )t  (2k1  k2 )  r )]} 
 E22 E1 exp{i[(2w2  w1 )t  (2k2  k1 )  r )]} 
Fotônica
 other terms
4. Interação Não Linear da Luz com a Matéria sem Absorção
Auto-difração
Considere alguns dos termos de diferença de freqüências:
Sinal #1
w
Meio
não linear
w
w w
2k1  k2
w w
Sinal #2
2k2  k1
E (r , t )3  E12 E2* exp{i[(2w1  w2 )t  (2k1  k2 )  r )]} 
 E22 E1* exp{i[(2w2  w1 )t  (2k2  k1 )  r )]} 

other ter
ms
+outros
termos
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Geometria de bombeio e prova
Um campo pode
contribuir com dois
fatores, um E e
outro E*.
Isto irá envolver
ambos somando e
subtraindo a
freqüência e seu
vetor k.
Sinal
w
w
E (r , t )  E1 E2 exp[i (w1t  k1  r )]
Este efeito é automaticamente
casado em fase!
Fotônica
amostra
w
3
2
 other
termstermos
+outros
w1  w1  w 2  w 2
k1  k1  k2  k2
4. Interação Não Linear da Luz com a Matéria sem Absorção
Porta de Polarização
Aqui o campo #2 contribui
com dois fatores, um E e o
outro E*.
Um é verticalmente
polarizado, enquanto o
outro é horizontalmente
polarizado. Isto resulta em
um sinal ortogonalmente
polarizado com o campo
E1.
Placa de onda
ajusta polarização a 45˚
w
w é rejeitado pelo
polarizador!
meio
não linear
Sinal
w
w
Se E1 é horizontalmente polarizado, o sinal será verticalmente polarizado:
*
E (r , t )3  E1h (E2h E2v
)exp[i(w1t  k1  r )] vˆ +...
Casado em fase automaticamente.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Interpretando estes fenômenos como grades induzidas
O padrão espacial de intensidade de dois feixes coerentes cruzados é
periódico, induzindo uma absorção ou índice de refração periódico no
meio – uma grade de difração!
x
k1
k2
k1  k cos zˆ
 k sin  xˆ
k 2  k cos  zˆ
 k sin  xˆ
*
Uma grade induzida é resultante dos termos cruzados da intensidade E1 E2

x x
x x

Re E1 exp i(wt  kz cos  kx sin   E2 exp  i(wt  kz cos  kx sin  
*
 Re exp  2ikx sin    cos(2kx sin  )
Fotônica
Franjas independentes
do tempo
4. Interação Não Linear da Luz com a Matéria sem Absorção
Difração de
uma grade
induzida
x
k1
k2
Um terceiro feixe será difratado em uma direção diferente.
Ele resulta de um feixe que é o produto de E1, E2*, e E3:
Esig  Psig   E1 E2*  E3
Este é um efeito genérico de mistura de quatro ondas.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
ex
grades induzidas
x
wex1
z
wex2
wpr
pr
sin
sinal
difratado
Considere:
wsig  wpr
wex1  wex 2  wex
Eex1  Eex 2  Eex
but kex1  kex 2
E (r , t )  E pr Eex exp{i[wsig t  (kex1  kex 2  k pr )  r ]}  ...
3
2
Condição de casamento de fase:
wsig  wex1  wex 2  w pr  w pr  ksig  k pr
k pol  kex1  kex 2  k pr  2kex sin ex xˆ   k pr cos  pr zˆ  k pr sin  pr xˆ 
O feixe difratado possui a mesma freqüência e magnitude de vetor k
como do feixe de prova, com outra direção.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Casamento de fase
em grades induzidas
Casamento de fase:
ksig  k pol
wex
ex
x
z
wex
wpr
sin
pr
k pol  2kex sin  ex xˆ   k pr cos  pr zˆ  k pr sin  pr xˆ 
ksig  k pr sin sig xˆ  k pr cos sig zˆ
Componente z: k pr
cossig zˆ  k pr cos pr zˆ
  sig    pr
Componente x:
O sinal de menos é
apenas o efeito de
excitação e prova
k pr sin pr xˆ  [2kex sinex  k pr sin pr ] xˆ
2
2

sin  pr 
sin  ex
2k pr sin pr   2kex sinex
 pr
ex
 pr
 sin pr  sinex
“Condição de Bragg”
ex
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
w
meio
não linear
Grades induzidas com
freqüências diferentes
w
w3
sinal
difratado
w w w3
Este efeito é chamado non-degenerate four-wave mixing.
Neste caso, as franjas de intensidade varrem o meio: uma
grade móvel.
E (t )3  E1 E2*E3 exp{i[(w1  w2  w3 )t  (k1  k2  k3 )  r ]}  ...
Condição de casamento de fase:
wsig  w1  w2  w3
k pol  k1  k2  k3
O cojunto possível de geometria de feixes é complexo!
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Acousto-optics involves diffracting light off a
grating induced by an acoustic wave.
An acoustic wave induces sinusoidal density, and hence sinusoidal
refractive-index, variations in a medium.
Acoustic
transducer
Pressure, density,
and refractive-index
variations due to
acoustic wave
Input
beam
w
Quartz
Diffracted
beam
w wacoustic
Acousto-optics works because acoustic waves have about the same
wavelengths as (visible) light waves. Such diffraction can be quite
strong: ~70%. Acousto-optics is the basis of useful devices.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Induced gratings with plane waves and more
complex beams (of the same frequency)
Two plane waves
A plane wave and
a
slightly distorted
wave
A plane wave and a
A plane wave
and a
very distorted
wave
slightly distorted wave
All such induced gratings will diffract a plane wave, reproducing
the distorted wave:
E and E are plane waves.
2
3
E (t )3  [E1 ( x, y)E2* ]E3 exp{i(k1  k2  k3 )  r }  ...
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Holography is an
induced-grating
process.
One of the write beams has a
complex spatial pattern—the
image. Different incidence angles
correspond to different fringe
spacings. Different object views
are stored as different fringe
spacings.
A third beam (a plane wave)
diffracts off the grating, acquiring
the image infor-mation.
Different fringe spacings
Theyield
light
phase
different diffraction angles––
stores the
hence 3D!
angular
info.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Phase conjugation
When a nonlinear-optical effect produces a light wave
proportional to E*, the process is called a phaseconjugation process. Phase conjugators can cancel out
Distorting
aberrations.
exp ikz  i  x, y  
exp ikz
 
medium
  x, y 
exp i  k  z  2i  x, y  


A normal mirror leaves
the sign of the phase
unchanged
exp i  k  z  i  x, y  
A phase-conjugate
mirror reverses the
sign of the phase
exp[i  k  z  i  x, y   i  x, y ]
exp i  k  z  i  x, y  
The second traversal through the medium cancels
out the phase distortion caused by the first pass!
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Phase conjugation = Time reversal
A light wave is given by:
E(x,y,z,t)  E0(x, y,z) exp[i(kz wt)]  E*0 (x,y,z) exp[i(kz  w t)]
If we can phase-conjugate the spatial part, we have:
Epc (x,y,z,t)  E0*(x, y, z) exp[i(kz  w t)]  E0 (x, y, z) exp[i(kz  w t)]
 E0*(x,y,z) exp[i(kz  w{t})]  E0 (x, y,z) exp[i(kz  w{t})]
 E0 (x, y, z) exp[i(kz w{t})]  E0*(x, y,z) exp[i(kz  w{t})]
Epc (x,y,z,t)  E(x, y,z,t)
Thus phase conjugation produces a time-reversed beam!
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Mistura de ondas degeneradas DFWM
Considere apenas processos com tres freqüências de
entrada e uma freqüência de saída que são idênticas.
freqüência idênticas = degeneradas.
w w w w
Como os vetores podem ter direções diferentes,
os numeraremos (como os campos):
k pol  k1  k2  k3
P
(3)
  0  E1 E E3
(3)
*
2
DFWM dá origem a uma quantidade enorme de efeitos interessantes.
Desejáveis ou não.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
DFWM com único campo
Se apenas um campo está envolvido, todos vetores k serão os mesmos,
Assim como os campos:
ksig  k1  k2  k3  k
E1  E 2  E3  E
A polarização se torna:
(3)
P
 0 
(3)
2
E E
DFWM com único campo dá origem a efeitos “auto” induzidos. Estes
incluem:
Auto-modulação de fase
Auto-focalização
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
DFWM  índice de refração não linear
Lembrando a equação:
2 E
1 2 E
2 P
 2 2  0 2
2
z
c0 t
t
E o envelope da polarização (termos linear e não linear):
2
2
(1)
(3)
(1)
(3)



P  0  E   E E  0    E  E




Substituindo a polarização na equação de onda (considerando pequena
variação lentano envelope de E comparada a 1/w):
2
2 E
1 2 E
2  E
(1)
(3)
 2 2  0 0     E  2
2

 t
z
c0 t
1   (1)   (3) E 2  2
2
 E
 E
2





1/
c


0
onde
0 0
0
2
2
2
z
c0
t
O índice de refração não linear é
Fotônica
n 
1
(1)
 
(3)
4. Interação Não Linear da Luz com a Matéria sem Absorção
E
2
DFWM  índice de refração não linear
O índice de refração na presença de polarizações lineares e não lineares:
n 
1 
(1)
 
(3)
E
2
O índice de refração usual (que denominamos n0) é:
Então:
n 
n  
2
0
(3)
 n0 1  
(3)
E
n0 
1   (1)
2
2
E / n02
Considerando que o termo não linear << n0:
2
n  n0 1   (3) E / 2n02 


n  n0  
(3)
2
E / 2n0
Uma vez que: I  E
Define-se o índice de refração não linear, n2:
n  n0  n2 I
Então:
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
2
A magnitude do índice de refração
magnitude e resposta temporal
Uma variedade de efeitos dão origem ao índice de refração não linear.
Aqueles que possuem grande valor de n2 tipicamente têm resposta lenta.
Efeitos térmicos produzem um grande efeito não linear através da
expansão térmica, devido à absorçã de energia, porém são tão lentos
quanto os processos térmicos difusivos.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Auto-focalização
Se o perfil do feixe for Gaussiano, então qualquer meio não linear possui
um índice derefração que é também Gaussiano:
n  n0  n2 I 0 exp(2r 2/ w20 )
Próximo a centro do feixe:
 n0  n2 I0 (1  2r 2/w02 )
A dependência da fase com a coodenada radial será:
 (r)  nk0 L  n0 k0 L  n2 k0 L I0 (1 2r 2 / w02 )
 (r)  constant  2n2 k0 L I0 (r 2 / w02 )
Que é precisamento o comportamento de lentes!
Nesta caso porém ele escala com a intensidade.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Small-scale self-focusing
Each tiny bump in the beam undergoes
its own separate self-focusing,
yielding a tightly focused spot inside
the beam, called a “filament.”
Intensity
If the beam has variations in intensity across its profile, it undergoes
small-scale self-focusing.
Position
Such filaments grow exponentially with distance.
And they grow from quantum noise in the beam, which is always there.
As a result, an intense ultrashort pulse cannot propagate through any
medium without degenerating into a mass of tiny highly intense filaments,
which, even worse, badly damage the medium.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Auto-modulação de fase e geração de contínuo
O pulso com auto-modulação de fase (SPM) desenvolve uma
dependênica da fase com o tempo proporcional a da intensidade
E0 ( z, t )  E0 (0, t ) exp ik0 n2 I (0, t ) z 
Isto é:
 ( z, t )  k0 n2 I (0, t ) z
Intensidade do pulso
no tempo
Quanto mais o pulos viaja,
maior a modulação.
Uma fase plana resulta em espectro estreito. Se consideramos que o
pulso inicia com fase plana, a SPM alarga o espectro.
Este não é um pequeno efeito! Uma variação de fase e centenas de
comprimentos de onda pode ocorrer!
Um espectro largo gerado desta forma é denominado Continuum.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
A freqüência instantânea x tempo na SPM
 ( z, t )  k0 z n2 I (t )
 ( z, t )
I (t )
winst (t )  
 k0 z n2
t
t
Um pulso de 10-fs, @ 800-nm que experimenta SPM com um
pico de magnitude igual a 1 radiano.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Pulso de SPM no domínio de freqüência
O mesmo pulso de 10-fs, @ 800-nm que experimenta SPM com
um pico de magnitude igual a 1 radiano.
É fácil, porém, alcançar vários radianos no retardo de fase.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Um pulso com alto SPM
Um pulso de 10-fs,
@ 800-nm que
experimenta SPM
com um pico de
magnitude igual a 1
radiano.
Note que o espectro alargou significativamente. Quando a SPM
muito forte, ela alarga muito o espectro. continuum generation.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Produção experimental do
continuum em uma fibra
Propagando pulsos de
500-fs @625nm através
de 30 cm de fibras
mono-modo.
The Supercontinuum
Laser Source, Alfano,
ed.
O espetro mais largo
ocorre para a maior
energia.
Fotônica
baixa
energia
energia
média
alta
energia
4. Interação Não Linear da Luz com a Matéria sem Absorção
Continuum generation simulations
Instantaneously responding n2; maximum SPM phase = 72 radians
Input Intensity
vs. time
(and hence
output phase
vs. time)
The Supercontinuum
Laser Source,
Alfano, ed.
Original spectrum is negligible in width compared to the output spectrum.
Output
spectrum:
Dw
Oscillations occur in spectrum because all frequencies occur twice
and interfere, except for inflection points, which yield maximum and
minimum frequencies.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Continuum generation simulation
Noninstantaneously responding n2; maximum SPM phase = 72 radians
Output phase vs.
time (≠ input
intensity vs. time,
due to slow
response)
Output spectrum:
Asymmetry in phase vs. time
yields asymmetry in spectrum.
The Supercontinuum
Laser Source, Alfano, ed.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Experimental continuum spectra
625-nm (70 fs and 2 ps) pulses in Xe gas
p = 15 & 40 atm
L = 90 cm
Input
wavelength
The Supercontinuum
Data taken by
Laser Source, Alfano, ed.
Corkum, et al.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Ultraviolet continuum
4-mJ 160-fs 308-nm pulses in 40 atm of Ar; 60-cm long cell.
Lens focal
length
= 50 cm.
Good quality output mode.
Fotônica
The Supercontinuum
Laser Source, Alfano, ed.
4. Interação Não Linear da Luz com a Matéria sem Absorção
UV Continuum in Air!
308 nm input pulse; weak focusing with a 1-m lens.
The Supercontinuum
Laser
Source,
Alfano, ed.
Continuum is limited when GVD causes the pulse to spread, reducing
the intensity.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Continuum Generation:
Good news and bad news
Good news:
It broadens the spectrum, offering a useful ultrafast white-light
source and possible pulse shortening.
Bad news:
Pulse shapes are uncontrollable.
Theory is struggling to keep up with experiments.
In a bulk medium, continuum can be high-energy, but it’s a
mess spatially.
In a fiber, continuum is clean, but it’s low-energy.
In hollow fibers, things get somewhat better.
Main problem: dispersion spreads the pulse, limiting the
spectral broadening.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Fibras ópticas micro-estruturadas
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Fibras ópticas micro-estruturadas modificam dispersão
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
O contínuo das fibras ópticas
micro-estruturadas é de
banda ultra-larga
Seção transversal
da fibra microestruturada.
O espectro extende-se
de ~400 a ~1500 nm e
é relativamente plano
(na média temporal).
O contínuo foi criado utiliazando pulsos
de laser de Ti:Sapphire sem amplificação
J.K. Ranka, R.S. Windeler, and A.J. Stentz, Opt. Lett. Vol. 25, pp. 25-27, 2000
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
O contínuo é meigo!
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Outros efeitos não-lineares de terceira ordem
absorção de dois fótons
Espalhamento
Raman
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção