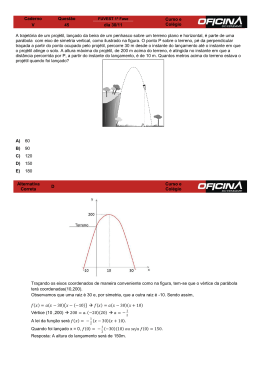
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
1. (Espcex (Aman) 2015) Um fabricante de poltronas pode produzir cada peça ao custo de
R$ 300,00. Se cada uma for vendida por x reais, este fabricante venderá por mês (600  x)
unidades, em que 0  x  600.
Assinale a alternativa que representa o número de unidades vendidas mensalmente que
corresponde ao lucro máximo.
a) 150
b) 250
c) 350
d) 450
e) 550
2. (Unicamp 2015) Seja a um número real. Considere as parábolas de equações cartesianas
y  x2  2x  2 e y  2x2  ax  3. Essas parábolas não se interceptam se e somente se
a) a  2.
b) a  2.
c) a  2  2.
d) a  2  2.
3. (Fuvest 2015) A trajetória de um projétil, lançado da beira de um penhasco sobre um terreno
plano e horizontal, é parte de uma parábola com eixo de simetria vertical, como ilustrado na
figura abaixo. O ponto P sobre o terreno, pé da perpendicular traçada a partir do ponto
ocupado pelo projétil, percorre 30 m desde o instante do lançamento até o instante em que o
projétil atinge o solo. A altura máxima do projétil, de 200 m acima do terreno, é atingida no
instante em que a distância percorrida por P, a partir do instante do lançamento, é de 10 m.
Quantos metros acima do terreno estava o projétil quando foi lançado?
a)
b)
c)
d)
e)
60
90
120
150
180
4. (Unifesp 2015) A concentração C, em partes por milhão (ppm), de certo medicamento na
corrente sanguínea após t horas da sua ingestão é dada pela função polinomial
C(t)  0,05t 2  2t  25. Nessa função, considera-se t  0 o instante em que o paciente ingere
a primeira dose do medicamento.
Página 1 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
Álvaro é um paciente que está sendo tratado com esse medicamento e tomou a primeira dose
às 11 horas da manhã de uma segunda-feira.
a) A que horas a concentração do medicamento na corrente sanguínea de Álvaro atingirá
40 ppm pela primeira vez?
b) Se o médico deseja prescrever a segunda dose quando a concentração do medicamento na
corrente sanguínea de Álvaro atingir seu máximo valor, para que dia da semana e horário
ele deverá prescrever a segunda dose?
5. (Unifesp 2014) Chamando de y’ e y” as equações das parábolas geradas quando a curva y
= 2x2–12x + 16 é refletida pelos eixos x e y, respectivamente, determine:
a) a distância entre os vértices das parábolas definidas por y’ e y”.
b) y’ e y”.
6. (Unicamp 2014) Sejam a e b reais. Considere as funções quadráticas da forma
f(x)  x2  a x  b, definidas para todo x real.
a) Sabendo que o gráfico de y  f(x) intercepta o eixo y no ponto (0,1) e é tangente ao eixo x,
determine os possíveis valores de a e b.
b) Quando a  b  1, os gráficos dessas funções quadráticas têm um ponto em comum.
Determine as coordenadas desse ponto.
7. (Enem 2014) Um professor, depois de corrigir as provas de sua turma, percebeu que várias
questões estavam muito difíceis. Para compensar, decidiu utilizar uma função polinomial f, de
grau menor que 3, para alterar as notas x da prova para notas y  f(x), da seguinte maneira:
- A nota zero permanece zero.
- A nota 10 permanece 10.
- A nota 5 passa a ser 6.
A expressão da função y  f(x) a ser utilizada pelo professor é
1 2 7
x  x.
25
5
1 2
y   x  2x.
10
1 2 7
y
x 
x.
24
12
4
y  x  2.
5
y  x.
a) y  
b)
c)
d)
e)
8. (Espcex (Aman) 2014) Uma indústria produz mensalmente x lotes de um produto. O valor
mensal resultante da venda deste produto é V(x)  3x2  12x e o custo mensal da produção é
dado por C(x)  5x2  40x  40. Sabendo que o lucro é obtido pela diferença entre o valor
resultante das vendas e o custo da produção, então o número de lotes mensais que essa
indústria deve vender para obter lucro máximo é igual a
a) 4 lotes.
b) 5 lotes.
c) 6 lotes.
d) 7 lotes.
e) 8 lotes.
Página 2 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
9. (Enem PPL 2013) O proprietário de uma casa de espetáculos observou que, colocando o
valor da entrada a R$10,00, sempre contava com 1.000 pessoas a cada apresentação,
faturando R$10.000,00 com a venda dos ingressos. Entretanto, percebeu também que, a partir
de R$10,00, a cada R$2,00 que ele aumentava no valor da entrada, recebia para os
espetáculos 40 pessoas a menos.
Nessas condições, considerando P o número de pessoas presentes em um determinado dia e
F o faturamento com a venda dos ingressos, a expressão que relaciona o faturamento em
função do número de pessoas é dada por:
a) F 
P2
 60P
20
b) F 
P2
 60P
20
c) F  P2  1200P
d) F 
P2
 60
20
e) F  P2  1220P
10. (Epcar (Afa) 2013) O gráfico de uma função polinomial do segundo grau y  f  x  , que tem
como coordenadas do vértice (5, 2) e passa pelo ponto (4, 3), também passará pelo ponto de
coordenadas
a) (1, 18)
b) (0, 26)
c) (6, 4)
d) (–1, 36)
11. (Fgv 2013) Uma única linha aérea oferece apenas um voo diário da cidade A para a cidade
B. O número de passageiros y que comparecem diariamente para esse voo relaciona-se com o
preço da passagem x, por meio de uma função polinomial do primeiro grau.
Quando o preço da passagem é R$ 200,00, comparecem 120 passageiros e, para cada
aumento de R$ 10,00 no preço da passagem, há uma redução de 4 passageiros. Qual é o
preço da passagem que maximiza a receita em cada voo?
a) R$ 220,00
b) R$ 230,00
c) R$ 240,00
d) R$ 250,00
e) R$ 260,00
12. (Fgv 2013) A editora fez também um estudo sobre o lançamento do livro em duas versões:
capa dura e capa de papelão. A pesquisa mostrou que, se a versão capa dura for vendida por x

reais e a versão capa de papelão por y reais, serão vendidos, no total, 130x  70y  x2  y2

exemplares das duas versões. Por uma questão de estratégia, o gerente de vendas decidiu
que a versão capa dura deve custar o dobro da versão capa de papelão.
a) Qual deve ser o preço de venda de cada versão, de modo que a quantidade de livros
vendida seja a maior possível?
b) Nas condições do item (a), quantos exemplares a editora estima vender no total?
13. (Mackenzie 2013) Sejam as funções f e g de
g(x)  5x  20. O valor de
a)
em
, definidas por f(x)  x2  4x  10 e
(f(4))2  g(f(4))
é
f(0)  g(f(0))
13
4
Página 3 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
13
2
11
c)
4
11
d)
2
e) 11
b)
14. (Enem 2013) A parte interior de uma taça foi gerada pela rotação de uma parábola em
torno de um eixo z, conforme mostra a figura.
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei
3
f(x)  x2  6x  C, onde C é a medida da altura do líquido contido na taça, em centímetros.
2
Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
Nessas condições, a altura do líquido contido na taça, em centímetros, é
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
15. (Enem PPL 2013) Uma pequena fábrica vende seus bonés em pacotes com quantidades
de unidades variáveis. O lucro obtido é dado pela expressão L(x) = −x2 + 12x − 20, onde x
representa a quantidade de bonés contidos no pacote. A empresa pretende fazer um único tipo
de empacotamento, obtendo um lucro máximo. Para obter o lucro máximo nas vendas, os
pacotes devem conter uma quantidade de bonés igual a
a) 4.
b) 6.
c) 9.
d) 10.
e) 14.
16. (Insper 2013) No gráfico estão representadas duas funções: f(x) do primeiro grau e g(x) do
segundo grau.
Página 4 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
O gráfico que melhor representa a função h(x) = f(x) + g(x) é
a)
b)
c)
d)
e)
Página 5 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
17. (Fgv 2013) A Editora Progresso decidiu promover o lançamento do livro Descobrindo o
Pantanal em uma Feira Internacional de Livros, em 2012. Uma pesquisa feita pelo
departamento de Marketing estimou a quantidade de livros adquirida pelos consumidores em
função do preço de cada exemplar.
Preço de venda
R$ 100,00
R$ 90,00
R$ 85,00
R$ 80,00
Quantidade vendida
30
40
45
50
Considere que os dados da tabela possam ser expressos mediante uma função polinomial do
1º grau y  a  x  b, em que x representa a quantidade de livros vendida e y, o preço de cada
exemplar.
a) Que preço de venda de cada livro maximizaria a receita da editora?
b) O custo unitário de produção de cada livro é de R$ 8,00. Visando maximizar o lucro da
editora, o gerente de vendas estabeleceu em R$ 75,00 o preço de cada livro. Foi correta a
sua decisão? Por quê?
18. (Mackenzie 2013) A função quadrática f, de
em , representada graficamente, com
raízes reais x1 e x 2 , tais que log0,64  x1 e log0,6  x2 é definida por:
1,25
5
3
a) f(x)  2x2  6x  4
b) f(x)  x2  6x  4
c) f(x)  2x2  6x  4
d) f(x)  x2  6x  4
e) f(x)  2x2  6x  4
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
A figura a seguir representa a evolução dos milhares de unidades vendidas de um produto em
função do tempo, dado em meses, desde seu lançamento.
Página 6 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
O trecho correspondente ao intervalo [0,t 1] pode ser representado pela expressão y  0,05x2 e
o trecho correspondente ao intervalo ]t1,t2] por y  0,05x2  4x  40.
19. (Insper 2013) O valor de t1 é
a) 5.
b) 10.
c) 15.
d) 20.
e) 25.
20. (Insper 2013) Considere que o ponto (t2,V) corresponde ao vértice da parábola de equação
y  0,05x2  4x  40. Nos últimos dez meses representados no gráfico, as vendas totais, em
milhares de unidades, foram iguais a
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
Página 7 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
Gabarito:
Resposta da questão 1:
[A]
O lucro L(x) será dado por (600  x)  (300  x). As raízes da função são 300 e 600, o valor de x
para que o lucro seja máximo é a média aritmética das raízes, portanto
xv  (300  600) : 2  450. Logo, o número de peças para que o lucro seja máximo, é:
600  450  150.
Resposta da questão 2:
[C]
Tem-se que
2x2  ax  3  x2  2x  2  x2  (a  2)x  1  0.
Logo, as parábolas não se intersectam se, e somente se, o discriminante da equação acima for
negativo, isto é, se
(a  2)2  4  1 1  0  (a  2)2  4
 | a  2 |  2.
Resposta da questão 3:
[D]
Adotando convenientemente um sistema de coordenadas cartesianas, considere a figura.
Sejam A o ponto de lançamento do projétil e a função quadrática f : [20, 20]  , dada na
forma canônica por f(x)  a  (x  m)2  k, com a, m, k 
k  200. Logo, sabendo que f(20)  0, vem
e a  0. É imediato que m  0 e
1
0  a  202  200  a   .
2
Portanto, temos f(x)  200 
x2
e, desse modo, segue que o resultado pedido é
2
Página 8 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
f( 10)  200 
( 10)2
 150 m.
2
Resposta da questão 4:
a) Queremos calcular o menor valor de t para o qual se tem C(t)  40. Assim, temos
0,05t 2  2t  25  40  (t  20)2  100
 t  10 h ou t  30 h.
A concentração do medicamento na corrente sanguínea de Álvaro atingirá 40 ppm pela
primeira vez às 11 10  21h da segunda-feira.
b) A concentração do medicamento na corrente sanguínea de Álvaro atingirá seu valor máximo
2
após 
 20 horas. Portanto, o médico deverá prescrever a segunda dose para as
2  ( 0,05)
20  (24  11)  7 horas da terça-feira.
Resposta da questão 5:
a) Observe o gráfico a seguir:
Considerando V o vértice da parábola de equação y = f(x), V’ o vértice de y’ = –f(x) e V” o
vértice de y” = f(–x) temos:
V(3, –2) , V’(3, –2) e V” (–3, –2)
Portanto, a distância entre os pontos V e V” será dada por:
d  (3  3)2  (2  2)2  52  2 13
b) Sendo y = f(x) = 2x2 – 12x + 16, temos:
y’ = – f(x) = – (2x2 – 12x + 16) = –2x2 + 12x – 16
Página 9 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
y” = f(–x) = 2(–x)2 –12(–x) + 16 = 2x2 + 12x + 16
Resposta da questão 6:
a) Se o gráfico de f intersecta o eixo das ordenadas em (0, 1), então b  1. Além disso,
como o gráfico é tangente ao eixo das abscissas, vem
Δ  0  a2  4  1 1  0
 a   2.
Portanto, a   2 e b  1.
b) Se a  b  1  b  1  a, então f(x)  x2  ax  1  a. Agora, sem perda de generalidade,
tomando a  0 e a  1, obtemos f1(x)  x2  1 e f2 (x)  x2  x, respectivamente. Ora, como os
gráficos de f1 e de f2 possuem um ponto em comum, tem-se x2  1  x2  x  x  1. Em
consequência, o resultado pedido é (1, 2).
Resposta da questão 7:
[A]
Seja f : [0, 10]  [0, 10], com f(x)  ax2  bx  c. Desse modo, temos
f(0)  0
f(5)  6
f(10)  10
c0
 25a  5b  6
100a  10b  10
a
7
5
c0
 b
1
25
.
Portanto, segue que f(x)  
1 2 7
x  x.
25
5
Resposta da questão 8:
[D]
Seja L(x) o lucro obtido, então:
L(x) = V(x) – C(x) = – 2x2 + 28x + 40
O valor de x para que L(x) seja máximo será dado por:
xV  
b
28

7
2a
2  ( 2)
Resposta da questão 9:
[A]
Sejam v o valor da entrada e n o número de aumentos de R$ 2,00. Logo,
v  10  2  n  n 
v  10
.
2
Página 10 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
Assim, temos
P  1000  40  n
v  10
2
 1200  20v.
 1000  40 
O que implica em v  60 
P
e, portanto,
20
P 
P2

F   60 

P


 60P.
20 
20

Resposta da questão 10:
[A]
Sendo V(xv, yv) o vértice de uma função polinomial do segundo grau dada por f(x) = ax2 + bx +
c. Toda função polinomial do segundo grau pode ser escrita através de sua forma canônica f(x)
= a  (x – xv)2 + yv.
Portanto, f(x) = a  (x – 5)2 + 2.
Como f(4) = 3, temos:
a  (4 – 5)2 = 3
a = 3.
Logo, f(x) = (x – 5)2 + 2.
Portanto, o ponto (1, 18) pertence ao gráfico da função, pois (1 – 5)2 + 2 = 18.
Resposta da questão 11:
[D]
Seja x o número de aumentos de R$ 10,00 no preço da passagem.
A receita de cada voo é dada pelo produto entre o preço da passagem e o número de
passageiros, ou seja,
R(x)  (200  10x)  (120  4 x)
 40  (x 20)  (x 30).
Logo, o número de aumentos que proporciona a receita máxima é
xv 
20  30
5
2
e, portanto, o resultado pedido é 200  10  5  R$ 250,00.
Resposta da questão 12:
a) Se x  2y, a quantidade de livros vendidos seria
130  2y  70y  (2y)2  y2  5y  (y  66).
Logo, o preço da versão capa de papelão que maximiza a quantidade vendida de livros é
Página 11 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
0  66
 R$ 33,00.
2
Portanto, o preço da versão capa dura deverá ser 2  33  R$ 66,00.
b) O resultado pedido é igual a 5  33  (33  66)  5445.
Resposta da questão 13:
[A]
f  4   42  4  4  10  10
g  f  4    g 10   5  10  20  30
f  0   02  4  0  10  10
g  f  0    b 10   30
Logo,
(f(4))2  g(f(4)) 102  ( 30) 130 13



.
f(0)  g(f(0))
10  ( 30)
40
4
Resposta da questão 14:
[E]
A abscissa do vértice da parábola y 
3 2
( 6)
x  6x  C é igual a 
 2.
3
2
2
2
Por outro lado, sabendo que o vértice da parábola pertence ao eixo das ordenadas, temos:
Δ
yv  
0
4a
( 6)2  4 
4
3
C
2
3
2
 6C  36  0
 C  6.
Portanto, segue-se que o resultado pedido é f(0)  C  6cm.
Resposta da questão 15:
[B]
Determinando o valor do x do vértice, temos:
xV 
12
6
2  ( 1)
Resposta da questão 16:
[C]
Como o gráfico de f passa pelos pontos ( 2, 0) e (0, 2), segue que f(x)  x  2. Além disso,
como o gráfico de g passa pelos pontos (0, 0) e (0, 1), temos que g(x)  ax2  ax, com a  0.
Portanto, h(x)  ax2  (a  1)x  2.
Página 12 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
Desse modo, o gráfico de h intersecta o eixo y no ponto de ordenada 2 e tem sua
concavidade voltada para cima.
A abscissa do vértice do gráfico de h é dada por
xv  
(a  1) 1 1 1
 
 .
2a
2 2a 2
Finalmente, como f(1)  3 e g(1)  0, segue que h(1)  f(1)  g(1)  3 e, portanto, o gráfico que
melhor representa a função h é o da alternativa [C].
Resposta da questão 17:
a) Tomando os pontos (30, 100) e (40, 90), segue que a taxa de variação da função
y  ax  b é igual a
a
90  100
 1.
40  30
Logo,
90  (1)  40  b  b  130.
Portanto,
y  x  130.
A função R :  , definida por R(x)  x  (x  130)  x  (x  130), fornece a receita obtida
com a venda de x livros. Logo, a quantidade a ser vendida, a fim de se obter a receita
máxima, é
xv 
0  130
 65.
2
Desse modo, o preço pedido é igual a y  65  130  R$ 65,00.
b) Seja L :

a função definida por
L(x)   x 2  130x  8x
  x2  122x
  x  (x  122),
que fornece o lucro obtido na venda de x livros (supondo que todos os livros produzidos são
0  122
 61.
vendidos). Logo, a quantidade a ser vendida para se obter o lucro máximo é
2
Para essa quantidade, o preço de venda unitário deveria ter sido
y  61 130  R$ 69,00.
Por conseguinte, a decisão do gerente não foi correta.
Resposta da questão 18:
[A]
Página 13 de 14
Exercícios de Aprofundamento – Matemática – Funções Quadráticas
5
log1,25 0,64  x1   
4
5
log 5 0,6  x2   
3
3
x2
x1


64
5
 
100
4
6
5
 
10
3
x2
x1

2
4
5
   
5
 
4
3
5
 
5
3
x2
x1
5
 
3
5
 
4
2
 x1  2
1
 x2  1
Logo,
f(x) = a.(x – (-2).(x – (-1))
f(x) = a.(x + 2).(x + 1)
Como f(0) = 4, temos:
a.(0+2).(0+1) = 4
2.a = 4
a=2
Logo, f(x) 2.(x + 2).(x + 1)
Ou seja, f(x) = 2x2 + 6x + 4.
Resposta da questão 19:
[D]
20  0,05  t1 
2
 t1 2  400
t1   20  como t1  0 
t1  20 meses.
Resposta da questão 20:
[E]
t2  b 2a   4 2 0,05   40
Nos últimos 10 meses as vendas totais serão dadas por:
y  40  – y  30  
 0,05  402  4  40 – 40 –  0,05  302  4  30 – 40  
 5 milhares de unidades.
Página 14 de 14