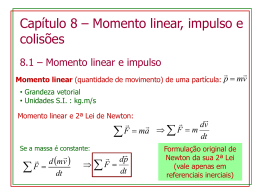
Sexta Aula teórica do ano dois mil e sete de nossa graça.
Conservação de
Momentum
Onde se explicam as regras seguidas pelas colisões
entre corpos extensos e suas aplicações no
cotidiano.
Compilado seguindo o exposto pelos sábios da
antiguidade, com comentários do autor.
Partindo da Segunda Lei de Newton
Fresul tan te  m a  m
dv

dt
p  mv
F
i
 Fres
i
F
i
i
 Fresultan te 
d ( p)
dt
d (m v )
dt
Uma questão Filosófica.
A conservação do momentum permite prever o
movimento dos corpos.
Mas, de onde vem a conservação do momentum?
Slide 4 – Onde continuamos a brincar com a
matemática na virtuosa tarefa de explicar o
movimento dos corpos.
Para um movimento que possua alguma constância no tempo:

( p)
Fi  Fresul tan te 
t
i
  t  Fi   ( p )
i
Relação semelhante pode ser obtida de forma mais geral e agradável aos olhos.
F

i
d ( p)
t2

dt
i
  F dt  
i
t1
i
t2
t1
d ( p)
dt
dt
De onde define-se uma nova grandeza denominada impulso.
t2
J 
  F dt  
i
t1
i
p2
p1
d ( p )  p 2  p1
Algumas generalidades sobre o
impulso
Nos casos em que for possível definir uma força média, é razoável escrever que
J  F m éd ( t 2  t1 )
De onde é possível inferir algum valor para esta grandeza no auxílio à
compreensão do movimento.
Uma aproximação gráfica ao
problema anteriormente descrito.
Slide 7 – Onde são feitas considerações sobre
momentum e energia.
K  W  F  r
Nem toda força varia a energia cinética.
J  p  F t
Toda força resultante produz variação no
momentum
Um exemplo em que o impulso pode ser
utilizado para maior compreensão do
movimento.
p 2  p1  J
Sobre o cálculo da força média no
caso previamente descrito.
Se o tempo da interação foi medido.
F t  p
Sendo
a
força
gravitacional desprezível
por ser pequena quando
comparada
a
força
exercida pela parede.
Colisão, uma simplificação ao
caso geral.
Uma colisão é um evento isolado no qual dois ou mais corpos
(ou partículas, ou pontos materiais) exercem uns sobre os
outros forças relativamente elevadas por um tempo
relativamente curto.
http://plato.if.usp.br/2-2004/fep2145d/AULAIQ/Aulas%20teoricas/col1.pdf
Séries de Colisões – momentum
transmitido por insistência.
r
Fm e d 
r
J
r
r
n
m r
 
p  
m v  
v
t
t
t
t
n
Um último aperitivo antes do prato
principal.
(F )x 
(F )y 
px
t
p y
t
Centro de Massa – Uma definição
prática.
CM
Simetria -> bela para a vista e útil para o cérebro.
CM
Centro de Massa – Uma definição
matemática.
N
rC M 
m 1 r1  m 2 r2  m 3 r3  ...  m N rN
m 1  m 2  m 3  ...  m N
xC M 
m 1  m 2  m 3  ...  m N
mx
i

i
i 1
N
m
i
i 1
N
yCM 
m 1 y1  m 2 y 2  m 3 y 3  ...  m N y N
m 1  m 2  m 3  ...  m N

i i

i 1
N
m
i 1
N
m 1 x1  m 2 x 2  m 3 x 3  ...  m N x N
mr
m
i
yi
i 1
N
m
i 1
i
i
Sobre a distribuição contínua de massas
(corpo rígido) e como localizar seu centro.
Para uma distribuição contínua:
x cm 
1
y cm 
xd m

M
1
M
 yd m
z cm 
1
zd m

M
Vamos tratar aqui somente de objetos uniformes, isto é, objetos que
possuem massa específica uniforme
 
dm
dV

r
1
rcm 
M
M
V
  dV  dm
 r d V

1
rd V

V
Slide 17 – Onde trata-se do movimento do
centro das massas de um corpo.
r
1
rcm 
M
n
r
d M rcm

d
dt
r
M a cm 
r
m i ri
i 1
dt
n
n
r
 m i ri
i 1
r
  M v cm 
r
 m ia i 
i 1
n

r
r
m iv i  P
i 1
r
r
 Fi  Fre s
n
i 1
Slide 18 - Onde aplica-se a terceira lei de
Newton para grande utilidade prática.
Continuando a jornada que nos leva a melhor compreensão dos fenômenos
naturais devemos agora considerar a existência de dois tipos de forças.
r
M a cm
r
  Fi 
r
M a cm 
r
 Fe xt
r
 Fe xt 
r 0
 Fin t
Alguns sistemas sem forças
externas.
Colisões
Uma colisão é um evento isolado no qual dois ou mais corpos
(os corpos que colidem) exercem uns sobre os outros forças
relativamente elevadas por um tempo relativamente curto.
Se não há forças externas no
momento da colisão
r
v cm 
r
r
m 1v 1  m 2 v 2
m1  m 2

http://www.universetoday.com/am/publish/spitzer_planetary_collision.html
r
P
M
Colisões Elásticas – aquelas em
que não há deformação.
r
r
r
r
m 1 v 1i  m 2 v 2 i  m 1 v 1 f  m 2 v 2 f
1
2
m 1v 
2
1i
1
2
m 2v
 m 1 v  m 2 v
2
1i
2
2i
2
2i

1
2
m 1v
 m 1v
2
1f
O sistema não perde energia cinética.
2
1f

1
2
 m 2v
m 2 v 2 f 
2
2
2f
Colisões Inelásticas
m 1 v 1i  m 2 v 2 i  m 1 v 1 f  m 2 v 2 f
Colisões Completamente
Inelásticas
m 1 v 1i  m 2 v 2 i  (m 1  m 2 )v f
Foguete = sistema isolado.
d p
dt
0
p1  p 2
p1  p 2  mv  ( m  dm )( v  dv )  (  dm )( v  v ex )
mdv   dvdm  v ex dm
m
dv
dt
  v ex
dm
dt
 Fres foguete   v ex
dm
dt