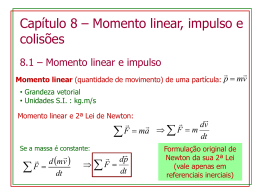
Unidade 14 – Conservação da
Quantidade de Movimentos
Forças internas e externas
Sistemas mecanicamente isolados
Colisões
Introdução
Quando descrevemos a atuação de uma
força, podemos fazê-lo dizendo que essa
força atuou em um determinado
deslocamento, ou seja, que essa força
realizou trabalho.
Mas também, descrever a atuação dessa
força dizendo que ela atuou durante
determinado intervalo de tempo.
Nessas condições, dizemos que a força
aplicou ao corpo um certo impulso.
Introdução
Da definição de impulso, obtemos a lei da
conservação da quantidade de
movimento, um dos pilares da descrição
física de nosso universo, tão abrangente
que mantém a sua validade mesmo nas
teorias mais atuais da Física Moderna.
Além das grandezas vetoriais impulso e
quantidade de movimento, discutiremos as
colisões, que podem ser descritas e
equacionadas de um modo relativamente
simples com a aplicação do princípio da
conservação da quantidade de movimento.
Introdução
Durante as colisões, os corpos trocam
forças muito intensas, que provocam
deformações neles.
Essas forças recebem o nome de
forças impulsivas, classificadas
como forças internas ao sistema
constituído pelos corpos envolvidas
em um choque.
Teorema do Impulso
Na figura 1 estão
representadas várias
forças agindo
simultaneamente sobre
um corpo de massa (m).
Essas forças podem ser
substituídas por uma
única: força
resultante, que
produzirá no corpo o
mesmo efeito dinâmico
que toda as demais.
Teorema do Impulso
Se a força resultante (R) agir sobre
um corpo, durante um dado intervalo
de tempo (∆t), diremos que a força
aplicará no coro um impulso (I),
dado por:
I = R.∆t
Teorema do Impulso
A grandeza vetorial impulso pode ser associada
a qualquer força que atue em um corpo durante
um intervalo de tempo e possui sempre a mesma
direção e o mesmo sentido da força que lhe
deram origem.
No SI, usamos as seguintes unidades: R em
newtons, ∆t em segundos e I em newtons .
segundos (N.s).
Quando uma força resultante não-nula age sobre
um corpo durante um intervalo de tempo, o
corpo sofre uma variação em sua velocidade.
Teorema do Impulso
Para estudar essa variação, vamos definir a grandeza
denominada quantidade de movimento (Q) pelo
produto da massa pela velocidade:
Q = m.v
A quantidade de movimento possui sempre a mesma
direção e o mesmo sentido da velocidade.
No SI, usamos as seguintes unidades: m em kg; v em
m/s e Q em kg . m/s
Teorema do Impulso
Com essas duas grandezas
– impulso e quantidade de
movimento – podemos
enunciar o teorema do
impulso:
O impulso resultante de um
sistema de forças sobre
corpo é igual à variação da
quantidade de movimento
do corpo.
Algebricamente:
I R = ∆Q
Lembrando que I = R.∆t e sendo
∆v = v - v 0 essa expressão pode
escrita assim :
(
R.∆t = m v - v 0
)
Observação
A intensidade de uma
força que produz um
impulso em um corpo
pode variar no
decorrer do tempo.
Nesse caso, o
módulo do impulso
produzido pela força
é obtido, no
diagrama horário F x
t, pelo cálculo da
área compreendida
entre o gráfico e o
eixo das abscissas,
no intervalo de
tempo considerando:
Exemplo 1
Exemplo 2
Sistemas isolados
Se pensarmos, por exemplo, em um
sistema constituído de um ímã e de
um bloco de ferro, diversas forças
atuarão sobre os corpos citados:
Sistemas isolados
F1,2 e F2, 1 constituem o
par de ação e reação de
forças magnéticas;
N1 e N2 são as reações
de apoio, ou seja as
forças normais em cada
um dos corpos;
P1e P2 são os resultados
das interações
gravitacionais entre
esses corpos e a Terra,
isto é, os pesos deles.
Sistemas isolados
Definido que o sistema é constituído apenas
pelo ímã e pelo bloco de ferro;
F1,2 e F2, 1 são consideradas forças
internas, pois são trocadas entre os
próprios corpos do sistema;
N1 e N2 são formadas por forças externas,
pois não faz parte do sistema, ou seja, as
normais são trocadas com o apoio;
P1e P2 são formadas por forças externas,
pois não faz parte do sistema, ou seja, os
pesos são trocadas com a Terra
Sistema isolados - conclusão
Um conjunto de corpos, ou de pontos
materiais, constitui um sistema no qual
podem agir forças internas e forças
externas.
Forças internas: são interações de dois
componentes do sistema. Quando
consideramos o sistema como um único
corpo e somamos todas as forças que agem
nesse sistema, a parcela relativa á soma
das forças internas é nula.
Sistema isolados
Forças extenas: são interações de um
componente do sistema com corpos que
não sejam do sistema. Se a soma das
forças externas que atuam no sistema for
nula, dizemos que se trata de um sistema
isolado de forças externas. Nesse caso,
como o somatório das forças são nulas, não
há variação na quantidade de movimento
do sistema.
Sistema Isolado
∑ F externas = 0 ⇒ Q sistema = cons tan te
Nessa expressão, para um sistema constituído de n elementos, temos
Q sistema = Q1 + Q2 + ... + Qn
Essa conclusão mostra-nos que a quantidade de movimento de cada
elemento do sistema pode variar, mas não varia a quantidade de
movimento do conjunto. Portanto:
Para um sistema isolado de forças externas, a quantidade de
movimento do sistema se conserva.
No caso particular de um sistema constituído por dois corpos (A e B) e
isolados de forças externas, temos:
Q incial = Q final ⇒ m A .v A + mB .v B = m A .v' A + mB .v'B
Exemplo
Exemplo - continuação
Exemplo de Aplicação -Modelo 1
Uma peça de artilharia
de massa 2 toneladas
dispara uma bala de 8
kg. A velocidade do
projétil no instante em
que abandona a peça
é 250 m/s. Calcule a
velocidade do recuo da
peça, desprezando a
ação de forças
externas.
PROCEDIMENTOS:
1. Represente a
peça de artilharia e a
bala antes e depois
do disparo;
2. Utilize o
princípio da
conservação da
quantidade de
movimento.
Exemplo de Aplicação -Modelo 1
Q antes = Q depois
0 = - v p ·2000 + 8 ·250
2000 v p = 2000
v p = 1 m/s
Colisões
Colisões
Nas colisões (choques), as interações
entre os corpos são de grande
intensidade e possuem magnitudes
que variam bruscamente durante
fenômeno.
Dentro da Dinâmica Impulsiva, ela
pode ser útil, por exemplo, para
explicar investigações e dados sobre
batida de automóveis.
Colisões
A figura mostra uma
colisão frontal de dois
veículos (A e B) que se
deslocam na mesma
direção;
Ma e mB as suas
massas;
VA e VB suas
respectivas velocidade
antes de colidirem;
V’A e V’B as velocidades
deles depois da
colisão:
Colisões
Recordando que os corpos envolvidos em
colisões constituem sistemas isolados e,
portanto, obedecem à conservação de
quantidade de movimento, então:
Qantes = Qdepois
Substituímos por:
m A .VA + mB .VB = m A .V ' A + mB .V ' B
Velocidade relativa
Se o corpo possui velocidade de 2m/s,
então, a cada 1s que passa, ele percorre
2m para direita;
De maneira similar, a cada 1s que passa, o
outro corpo, percorre 3 m para esquerda;
Portanto eles se aproximam um total de
5m.
Assim podemos dizer que a velocidade de
aproximação entre os corpo foi de 5m/s.
Velocidade relativa
Como poderíamos obter o mesmo
resultado sem que haja a necessidade
desse raciocínio?
A maneira mais fácil é subtrair as
velocidades e respeitando seus
respectivos sinais.
Vaprox = VA - VB
Velocidade relativa
Após uma colisão, nem sempre temos uma
fase de afastamento, pois os corpos podem
permanecer grudados depois de sofrerem o
choque.
Apesar disso, em nossos estudos, sempre
consideremos essa fase (mesmo que a
velocidade de afastamento seja nula).
Seguindo o mesmo raciocínio da velocidade
relativa de aproximação, os corpos A e B se
afastam com velocidade Vaf (velocidade
relativa de afastamento), que também pode
ser calculada com subtração:
Vafast = VB – VA
Exemplo de Aplicação -Modelo 2
Uma bomba de massa 600 kg tem
velocidade de 50 m/s e explode em duas
partes. Um terço da massa é lançada para
trás com velocidade de 30 m/s. Determine
a velocidade com que é lançada a outra
parte.
PROCEDIMENTOS:
1. Represente a bomba antes da explosão, e
as partes da bomba após a explosão;
2. Use Qantes =Qdepois. (Observe a orientação)
Exemplo de Aplicação -Modelo 2
Fases de uma colisão
Em choque entre dois
corpo, temos a
tendência de estudar o
ocorre, como se um
fenômeno único,
indivisível, estivesse
acontecendo.
Durante uma colisão,
por exemplo, podemos
supor existência de
pelo menos, duas
fases distintas: a de
deformação e a de
restituição.
Fases de uma colisão
Fase de deformação
Fases de uma colisão
Fase de restituição
Exemplo de Aplicação – Modelo 3
Dois corpos A e B
movimentam-se na
mesma direção e
possuem velocidades de
módulo 3m/s e 2m/s.
Calcule a velocidade
relativa entre eles se
suas velocidades tiverem
o mesmo sentido e se
tiverem sentidos
opostos.
Resposta:
Apesar de muito usada,
essa regra não é valida,
pois a velocidade relativa
entre os dois é sempre a
diferença entre as
velocidades,
considerando-se seus
respectivos sinais.
Para que pudéssemos
usar a regra da soma ou
da diferença, teríamos de
fazer os cálculos com os
módulo das velocidades
dos corpos.
Coeficiente de restituição
Quando começamos a estudar as colisões,
percebemos que a equação da conservação
da quantidade de movimento era
necessária para podermos quantificar
choques, mas insuficiente no caso de
termos situações com sua incógnitas.
Veremos outra expressão matemática que
poderá ser usada em casos como esse na
constituição de um sistema de equações.
Coeficiente de restituição
Ao pensarmos, por exemplo, numa batida entre
dois carros e numa bolinha de golfe que é
golpeada, perceberemos semelhanças muito
claras: os dois fatos analisados são colisões, mas
os formatos dos corpos envolvidos sofrem
restituições percentualmente diferentes.
Essas duas situações mostram que cada colisão
apresenta um certo nível ou percentual de
restituição.
Para os carros, teríamos praticamente 0% e,
para a bolinha, quase 100% de restituição.
Coeficiente de restituição
De forma geral, devemos pensar que, em
qualquer tipo de choque, existe um
coeficiente de restituição (e) que compara
dados dos corpos envolvidos antes e depois
do contato entre eles.
Matematicamente, isso pode ser
representado pela seguinte equação:
e=
vafast
vaprox
v ' B −v ' A
=
v A − vB
Tipos de Choque
Se analisarmos um sistema de corpos que sofrem
uma colisão, poderão ocorrer perdas de energia
cinética em virtude de aquecimento, deformação e
som provocados no impacto.
Choque inelástico, anelástico ou
plástico
a)
b)
c)
d)
e=0
Qfinal = Qinicial (a quantidade de movimento do
sistema se conserva
Ec final < Ec inicial (não há conservação de energia
cinética;
Perda de energia no processo:
2
Ecantes
2
m .(V ) m .(V )
= A A + B B
2
2
2
Ecdepois
m + mB .(VA − VB )
= A
2
Perda = Ecantes − Ecdepois
e)
f)
Só existe a fase de deformação
Os corpos movem-se juntos após o choque (ficam
"grudados")
Choque parcialmente elástico
a)
b)
c)
d)
0<e<1
Qfinal = Qinicial (a quantidade de movimento do
sistema se conserva)
Ec final < Ec inicial (parte da energia cinética se converte
em outras formas de energia, notadamente, calor e
som)
Perda de energia no processo:
e) Existem as fases de deformação e de restituição
f) Equacionamento:
(1) ma.va+ mb.vb = ma.v'a + mb.v'b
(2) e. (v'a - v'b) = - (va - vb)
Choque perfeitamente elástico
a) e = 1, logo, Vapro = - Vafast
b) Qfinal = Qinicial (a quantidade de movimento do sistema
se conserva)
c) Ec final = Ec inicial (a energia cinética do sistema se
conserva)
d) Existem as fases de deformação e de restituição
e) Equacionamento (fixar inicialmente o eixo de
movimento para referência de sinais):
(1) ma.va+ mb.vb = ma.v'a + mb.v'b
(2) (v'a - v'b) = - (va - vb)
Exemplos de Aplicação – Modelo 4
a) Uma esfera de massa m = 5,0kg e velocidade de 3,0m/s, choca-se
com outra esfera idêntica, inicialmente em repouso. Admitindo-se o
choque elástico e frontal, determine a velocidade das esferas após o
choque.
m A .v A + mB .vB = m A .v' A + mB .v'B
Como o choque é elástico, e = 1.Logo :
v ' B −v ' A
v ' B −v ' A
e=
→1 =
→ v' B −v' A = 5
v A − vB
5
5.3 + 0 = 5.v' A + mB .v' B
v' B = 5 + v' A (2)
Q antes = Q depois
15 = 5(v' A +v'B )
v' A + v' B = 3 (1)
Exemplos de Aplicação – Modelo 4
(1) → (2) ⇒ v' A +v'B = 3 → v' A +(5 + v' A ) = 3
→ 2v' A +5 = 3 → 2v' A = −2 ∴ v ' A = −1m / s
v'B = 5 + v' A → v' B = 5 + (− 1) →
v ' B = 4m / s
Exemplos de Aplicação – Modelo 5
Exemplos de Aplicação – Modelo 6
Exemplos de Aplicação – Modelo 6
Exemplos de Aplicação – Modelo 6
d) Um projétil de
massa m = 15g
atinge um corpo de
teste de 10kg do
aparelho pêndulo
balístico. A medida
da altura de 5 cm.
Determine a
velocidade do
projétil antes do
impacto
M +m
v=
. 2 g.h
m
(
)
10 + 15.10 −3
−2
v=
.
210
.
5
.
10
15.10 −3
v = 667,7 m / s