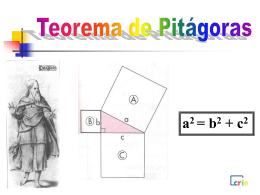
MATEMÁTICA E SUAS
TECNOLOGIAS - Matemática
Ensino Médio, 1ª Série
Teorema de Pitágoras e Aplicações
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Vamos Participar?
A escola estadual do bairro está promovendo a gincana
“Aprendendo com os outros”. As equipes participantes
são compostas por seis alunos: dois do primeiro ano,
dois do segundo e dois do terceiro ano do Ensino
Médio. São três equipes inscritas: “Vamos que vamos”,
“Sempre em frente” e “Lutando é que se vence”. Os
alunos estão animados e torcendo por sua equipe
favorita.
Qual a equipe que você acha que vai vencer a gincana?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Sorteio das atividades
A primeira atividade da gincana é resolver um
desafio matemático. Cada equipe com um desafio
diferente. Para saber o seu, um representante de
cada equipe pega uma ficha numerada dentro de
uma caixa.
Qual será o desafio mais fácil? E o mais difícil?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Equipe “Vamos que vamos”
A equipe “Vamos que vamos” tirou a ficha 1 que
corresponde ao seguinte desafio:
Represente, com uma corda de 12 metros
de comprimento, um triângulo que tenha
um dos ângulos reto (medindo 90º).
Você consegue resolver esse desafio?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Solução da equipe “Vamos que vamos”
A equipe resolveu o desafio desse modo:
-Dobrou a corda ao meio várias vezes até encontrar a medida
de um metro aproximadamente;
- Marcou essa medida com um nó.
-Depois marcou outros nós com espaçamento de um metro,
aproximadamente, entre cada nó.
-Ao final da marcação, a corda tinha 12 nós, incluindo os das
pontas.
-Três componentes da equipe esticaram a corda no chão,
formando um triângulo.
- O triângulo formado ficou com 5, 4 e 3 metros cada lado.
Você acha que a equipe resolveu o desafio?
Onde está o ângulo reto?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Você Sabia?
“Conta-se que, para obter ângulos retos, usados
para medir as terras após as enchentes do rio Nilo,
os “esticadores de corda” utilizavam uma corda com
12 nós, cuja distância um do outro era igual e, com
ela, construíam um triângulo com os vértices desses
nós.
O triângulo assim obtido possui lados que medem 3,
4 e 5 unidades de comprimento e é um triângulo
retângulo, isto é, um de seus ângulos internos mede
90º.”(DANTE, 2005, p.163)
Gostou da descoberta?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Observe a imagem dos
“esticadores de corda”
Imagem: (a) Triângulo / Tosha / Public Domain e (b) Encyclopaedia Biblica, 1903 / Public Domain.
Achou interessante?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Equipe “Sempre em frente”
A equipe “Sempre em frente” tirou a ficha 2 que
corresponde ao seguinte desafio:
Represente, num papel quadriculado, um
triângulo com o tamanho dos lados
distintos, mas que tenha um dos ângulos
reto (medindo 90º).
Você consegue resolver esse desafio?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Solução da equipe “Sempre em frente”
Alguns componentes da equipe resolveram o desafio de modo
diferente.
Paulo fez a seguinte representação:
Você acha que Paulo resolveu o desafio?
Onde está o ângulo reto?
MATEMÁTICA, 1º Ano
Teorema de Pitágoras e Aplicações
Solução da equipe “Sempre em frente”
Já Ana fez a seguinte representação:
Você acha que Ana resolveu o desafio?
Todos os lados têm tamanhos distintos?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Solução da equipe “Sempre em frente”
João comentou:
-Os dois estão certos e os dois estão errados.
-Paulo acertou, pois o tamanho dos lados do triângulo
são distintos, mas errou porque não apresentou
nenhum ângulo reto.
- Ana acertou, pois há um ângulo reto, mas errou
porque dois lados do triângulo apresentaram o
tamanho igual.
Você concorda com João?
Você propõe alguma solução?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Solução da equipe “Sempre em frente”
João propõe:
-Vamos juntar as ideias e fazer um triângulo com
tamanhos de lados distintos e com um ângulo reto.
Você concorda com João?
Você propõe outra solução?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Equipe “Lutando é que se vence”
A equipe “Lutando é que se vence” tirou a ficha 3,
que corresponde ao seguinte desafio:
Construa quadrados de áreas 25 cm²,
16cm² e 9 cm². Depois, prove que os dois
quadrados menores cabem no quadrado
maior.
Você consegue resolver esse desafio?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Solução da equipe “Lutando é que se vence”
A equipe resolveu o desafio desse modo:
-Primeiro desenhou os três quadrados com a área solicitada
em papel cartolina.
-Depois recortou os três quadrados para poder manipulá-los.
-Manteve o quadrado maior intacto.
-Fez cortes nos dois quadrados menores de modo que eles
formassem um quebra-cabeça de figuras geométricas.
-Ao juntar as peças desse quebra-cabeça, encontrou um
quadrado de mesmo tamanho do quadrado maior.
Você acha que a equipe resolveu o desafio?
Que tal tentar fazer o mesmo que a equipe “Lutando é que se vence”
fez?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
O que a equipe “Lutando é que se vence”
provou?
Ao resolver o desafio, a equipe provou que “a soma da
área dos quadrados menores é igual a área do quadrado
maior.”
Recordando a solução da equipe “Vamos que vamos”,
veremos que o triângulo formado tinha 3, 4 e 5 metros.
Se pensarmos um pouco, perceberemos que tais medidas
correspondem aos lados dos quadrados utilizados no
desafio da equipe “Lutando é que se vence”.
Você consegue deduzir algo com isso?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Alguém no passado conseguiu perceber.
Um famoso filósofo e matemático grego chamado Pitágoras
percebeu uma relação entre esses valores e conseguiu
deduzir e provar em outras situações que
Em todo triângulo retângulo, o quadrado da medida da
hipotenusa é igual à soma dos quadrados da medida dos
catetos.
Ele considerou a hipotenusa como o lado oposto ao ângulo
reto.
Os outros dois lados ficaram conhecidos como cateto.
Achou interessante?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
O Teorema de Pitágoras
a
c
b
a² = b² + c²
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
E a gincana, quem ganhou?
As três equipes acertaram o desafio matemático.
Agora vão encarar as questões de história.
Isso, porém, é outra história que, um dia, conto para
vocês.
Agora é a nossa vez de pensar
e resolver desafios.
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Sua vez de responder
1- A medida dos lados do
triângulo na figura ao lado são a,
b e c. Complete as frases.
B
a) b e c indicam a medida dos
____________ e a indica a
medida da _____________.
b) A área dos quadrados
construídos junto dos catetos são
iguais a ________ e _________.
c) A área do quadrado construído
junto da hipotenusa é igual a
____________.
a
c
A
b
C
As atividades relativas a essa figura
também foram inspiradas em questões
do mesmo livro.
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
2- Ainda observando a figura anterior, escreva uma relação
entre a área do quadrado maior e a área dos quadrados
menores.
_________________________________________________
_________________________________________________
_________________________________________________
3- Você acabou de criar uma relação própria para o Teorema
de Pitágoras. Agora complete a afirmação abaixo:
“Num triângulo retângulo, o quadrado da medida da
________________ é igual à soma dos _______________
da medida dos _______________.”
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
4- Qual das alternativas tem valores que correspondem à
medida dos lados de um triângulo retângulo?
a)
b)
c)
d)
7, 10 e 11
9, 10, 15
9, 12, 15
3, 4, 9
Justifique sua resposta: __________________________
_______________________________________________
_______________________________________________
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
5- Descubra o valor de x nos triângulos retângulos abaixo:
C
a)
b)
C
25
B
A
13
12
A
x
B
24
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
6 - O portão de entrada de uma casa tem 4 metros na
base e 3 metros na altura. Qual o comprimento que teria
uma trave de madeira colocada na diagonal desse
portão?
7 – Qual a medida da hipotenusa de um triângulo
retângulo isósceles cujo cateto mede 1cm?
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
8- Para determinar a medida dos lados de um tabuleiro
quadrado de área igual a 100cm², Angélica pensou em
calcular √100.
a) O que você acha da forma como Angélica pensou?
Justifique sua resposta.
b) Que resultado Angélica obterá?
Questão retirada do volume 4 da coleção Viver, Aprender
PNLD EJA 2011 (p.133)
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
9 – Qual é o comprimento aproximado da escada da figura
abaixo?
4m
7m
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
9 – A figura abaixo é um trapézio isósceles, cuja medida está
expressa em centímetros. Nessas condições, vamos calcular:
14
D
C
4
A
E
20
F
B
a) A medida x de cada lado não paralelo do trapézio.
b) O perímetro do trapézio ABCD.
Questão retirada do livro A conquista da Matemática – 4ª etapa EJA (2001, p.176)
MATEMÁTICA, 1ª Série
Teorema de Pitágoras e Aplicações
Referências Bibliográficas
DANTE, L. R. Tudo é Matemática. 8ª série. São
Paulo: Ed. Ática, 2005.
GIOVANNI, J. R. A Conquista da Matemática. 4ª
etapa da EJA São Paulo : Ed. FDT, 2001.
Vários autores. Coleção Viver, Aprender. Vol. 4 EJA. São Paulo: Ed. Global, 2009.
Tabela de Imagens
Slide
7a
Autoria / Licença
(a)Triângulo / Tosha / Public Domain.
Link da Fonte
Data do
Acesso
http://commons.wikimedia.org/wiki/File:%D0%9 18/04/2012
5%D0%B3%D0%B8%D0%BF%D0%B5%D0%B4%D
0%BA%D0%B8%D0%B9_%D1%82%D1%80%D0%
B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%
D0%BD%D0%B8%D0%BA.svg
7b (b) Encyclopaedia Biblica, 1903 / Public Domain. http://commons.wikimedia.org/wiki/File:C%2BB- 18/04/2012
Agriculture-Fig3.PNG