RESOLUÇÃO DA PROVA DE MATEMÁTICA DO VESTIBULAR 2013 DA
UNICAMP-FASE 2.
RESOLUÇÃO: PROFA. MARIA ANTÔNIA C. GOUVEIA
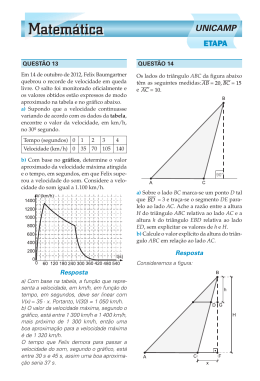
13. Em 14 de outubro de 2012, Felix Baumgartner quebrou o recorde de velocidade em queda livre. O
salto foi monitorado oficialmente e os valores obtidos estão expressos de modo aproximado na tabela e no
gráfico abaixo.
a) Supondo que a velocidade continuasse variando de acordo com os dados da tabela, encontre o valor da
velocidade, em km/h, no 30o segundo.
Tempo (segundos)
Velocidade (km/h)
0
0
1
35
2
70
3
105
4
140
b) Com base no gráfico, determine o valor aproximado da velocidade máxima atingida e o tempo, em
segundos, em que Felix superou a velocidade do som. Considere a velocidade do som igual a 1.100 km/h.
RESOLUÇÃO:
a) Ao analisar a variação da velocidade na linha 2 da tabela em relação a t ∈ {1s, 2s, 3s, 4s, ...} verifica-se
que seus valores formam uma P.A. com primeiro termo igual a 35 e razão 35, logo para t = 30s tem-se: V
= 35 + (30 – 1)× 35 = 35 + 1015 = 1050.
RESPOSTA: 1050 km/h.
b) Analisando o gráfico vê-se que
1300km/h < Vmáx < 1400km/h e ainda que
2700
1300km/h < Vmáx <
km/h, então pode-se
2
dizer aproximadamente 1325 km/h.
Vê-se também que o primeiro instante t em que
Vmáx > 1100km/h é um valor em que
30 < t < 45, pode-se tomar 37s, por exemplo,
RESPOSTA: 1325 km/h e 37s.
1
14. Os lados do triângulo ABC da figura abaixo têm as seguintes medidas AB = 20 , BC = 15 e
AC = 10 .
a) Sobre o lado BC marca-se um ponto D tal que BD = 3 e traça-se o segmento DE paralelo a AC. Ache
a razão entre a altura H do triângulo ABC relativa ao lado AC e a altura h do triângulo EBD relativa ao
lado ED, sem explicitar os valores h e H.
b) Calcule o valor explícito da altura triângulo ABC em relação ao lado AC.
RESOLUÇÃO:
a) Como
BC 15
H
=
= 3⇒ = 3.
BD 3
h
RESPOSTA: 3.
b) Do triângulo BCF: H2 = 225 – x2 e do triângulo BAF:
H2 = 400 – (10 + x)2. Logo: 225 – x2 = 400 – (10 + x)2.
225 – x2 = 400 – (10 + x)2 ⇒ 175 + x2 – 100 – 20x – x2 = 0 ⇒
20x = 75 ⇒ x =
15
225
3375
15 15
⇒ H 2 = 225 −
⇒ H2 =
⇒H=
4
16
16
4
15 15
.
RESPOSTA:
4
15. A superfície de um reservatório de água para abastecimento público tem 320. 000m2 de área, formato
retangular e um dos seus lados mede o dobro do outro. Essa superfície é representada pela região
hachurada na ilustração abaixo. De acordo com o Código Florestal, é necessário manter ao redor do
reservatório uma faixa de terra livre. Denominada Área de Proteção Permanente (APP), como ilustra a
figura abaixo. Essa faixa deve ter largura constante e igual a 100m, medidos a partir da borda do
reservatório.
a) Calcule a área da faixa de terra denominada APP nesse caso.
b) Suponha que a água do reservatório diminui de acordo com a expressão V(t) = V0.2– t, em que V0 é o
volume inicial e t é o tempo decorrido em meses. Qual é o tempo necessário para que o volume se reduza
a 10% do volume inicial? Utilize, se necessário, log102 ≈ 0,30.
2
RESOLUÇÃO:
a) A faixa de terra denominada APP é formada por dois
retângulos de dimensões (2x)m × 100m, dois retângulos
xm × 100m e 4 semicírculos de 100m de raio.
Como a superfície do reservatório de água tem 320. 000m2
de área, 2x.x = 320.000 ⇒ x2 = 160.000 ⇒ x = 400 m.
A área da faixa de terra denominada APP é então:
SAPP = 1002 π + 2 × 800 × 100 + 2 × 400 × 100 ⇒
SAPP = 10000π + 240000 = 10000(π + 24).
RESPOSTA: 10000( π + 24)
m2.
b) Como o questionamento é “Qual é o tempo necessário para que o volume se reduza a 10% do volume
inicial?”, tem-se:
V
1
1 10
1
1
V0 .2 − t = 0 ⇒ 2 − t =
⇒ log10 (2− t ) = log10   ⇒ − tlog10 (2) = −1 ⇒ t =
=
=3 ⇒
10
10
10
0,3
3
3
 
Aproximadamente t = 3me10d
RESPOSTA: t = 3me10d.
16. A numeração dos calçados obedece a padrões distintos, conforme o país. No Brasil, essa numeração
varia de um em um, e vai de 33 a 45, para adultos. Nos Estados Unidos a numeração varia de meio em
meio, e vai de 3,5 a 14 para homens e de 5 a 15,5 para mulheres.
a) Considere a tabela abaixo.
Comprimento do calçado ( x )
Numeração brasileira ( t )
35
23,8 cm
42
27,3 cm
Suponha que as grandezas estão relacionadas por funções afins t(x) = ax + b para a numeração brasileira e
x(t) = ct + d para o comprimento do calçado. Encontre os valores dos parâmetros a e b da expressão que
permite obter a numeração dos calçados brasileiros em termos do comprimento, ou os valores dos
parâmetros c e d da expressão que fornece o comprimento em termos da numeração.
b) A numeração dos calçados femininos nos Estados Unidos pode ser estabelecida de maneira
aproximada pela função real f definida por f (x) = 5(x − 20) / 3 , em que x é o comprimento do calçado
em cm.
Sabendo que a numeração dos calçados nk forma uma progressão aritmética de razão 0,5 e primeiro
termo n1= 5 , em que nk = f(ck) , com k natural, calcule o comprimento c5 .
RESOLUÇÃO:
t(23,8) = 35 23,8a + b = 35 − 23,8a − b = −35 3,5a = 7 a = 2
a) 
⇒
⇒
⇒
⇒
t(27,3) = 42 27,3a + b = 42 27,3a + b = 42
a = 2
b = −12,6
7c = 3,5
x(35) = 23,8 35c + d = 23,8 − 35c − d = −23,8 
c = 0,5
⇒
⇒
⇒




1 ⇒
x(42)
=
27,3
42c
+
d
=
27,3
42c
+
d
=
27,3
c
=



d = 6,3

2
RESPOSTA: a = 2; b = −12,6; c = 0,5 e d = 6,3
5(c k − 20)
b) Sendo nk = f(ck) e f (x) = 5(x − 20) / 3⇒ n k =
.
3
Como a numeração dos calçados nk forma uma progressão aritmética de razão 0,5 e n1= 5 ⇒
5(c5 − 20)
121
n5 = 5 + (5 – 1).0,5 = 5 + 2 = 7 ⇒ 7 =
⇒ 21 = 5c5 − 100 ⇒ 5c5 = 121 ⇒ c5 =
= 24,2 .
3
5
RESPOSTA: c5 = 24,2.
3
17. Na formulação de fertilizantes, os teores percentuais dos macronutrientes N, P e K, associados
respectivamente a nitrogênio, fósforo e potássio, são representados por x , y e z .
3x + y − z = 0,20

a) Os teores de certo fertilizante satisfazem o seguinte sistema de equações lineares: 2y + z = 0,55
z = 0,25

Calcule x e y nesse caso.
b) Suponha que para outro fertilizante valem as relações 24% ≤ x + y + z ≤ 54%, x ≥ 10%,
y ≥ 20% e z = 10%. Indique no plano cartesiano abaixo a região de teores (x, y) admissíveis para tal
fertilizante.
RESOLUÇÃO:
3x + y − z = 0,20
3x + y − 0,25 = 0,20 3x + y = 0,45  y = 0,15

a) 2y + z = 0,55
⇒
⇒
⇒
2 y + 0,25 = 0,55
2 y = 0,30
 x = 0,10
z = 0,25

RESPOSTA: x= 0,10 e y = 0,15.
b) Se 24% ≤ x + y + z ≤ 54%, x ≥ 10%, y ≥ 20% e z =
10% ⇒ 14% ≤ x + y ≤ 44% e x + y ≥ 30% ⇒
30% ≤ x + y ≤ 44% ⇒
x + y ≥ 30% e y ≤ − x + 44%
Para y = 20% ⇒ x = 24% ou x = 10% e para x = 10%
⇒ y = 34% ou x = 10%
RESPOSTA: A região de teores (x, y) admissíveis
para tal fertilizante é a região determinada pelo
triângulo de vértices B = (10%, 20%); C = (24%,
20%) e A= (10%, 34%).
4
18. O diagrama abaixo indica a distribuição dos alunos matriculados em três cursos de um a escola. O
valor da mensalidade de cada é de R$ 600,00, mas a escola oferece descontos aos alunos que fazem mais
de um curso. Os descontos, aplicados sobre o valor total da mensalidade, são de 20% para quem faz dois
cursos e de 30% para os matriculados em três cursos.
a) Por estratégia de marketing, suponha que a escola decida divulgar os percentuais de desconto,
calculados sobre a mensalidade dos cursos adicionais e não sobre o total de mensalidade. Calcule o
percentual de desconto que incide sobre a mensalidade do segundo curso para aqueles que fazem dois
cursos e o percentual de desconto sobre o terceiro curso para aqueles que fazem três cursos.
b) Com base nas informações do diagrama, encontre o número de alunos matriculados em pelo menos
dois cursos. Qual a probabilidade de um aluno, escolhido ao acaso, estar matriculado em apenas um
curso?
RESOLUÇÃO:
a) Projeto original de desconto para os alunos que fazem dois cursos: 2 × 600 × 0,20 = 240 reais.
Projeto original de desconto para os alunos que fazem três cursos: 3 × 600 × 0,30 = 540 reais.
240
= 0,40 = 40%
Por estratégia de marketing, para os alunos que fazem dois cursos, o desconto é de
600
540
sobre o segundo curso. Para os alunos que fazem três cursos, o desconto é de
= 0,90 = 90% sobre
600
o terceiro curso.
RESPOSTA: 40% e 90%.
b) De acordo com o diagrama, o número total de alunos matriculados na escola (espaço amostral) é
9 + 7 + 3 + 4 + 8 + 2 + 6 = 39, e o total de alunos matriculados em apenas um dos três cursos é
9 + 6 + 8 = 23.
23
Então a probabilidade de um aluno, escolhido ao acaso, estar matriculado em apenas um curso:
39
RESPOSTA:
23
.
39
19. Considere a família de retas no plano cartesiano descrita pela equação
(2 − p)x + (2 p +1) y + 8 p + 4 = 0 , nas variáveis x e y , em que p é um parâmetro real.
a) Determine o valor do parâmetro p para que a reta correspondente intercepte perpendicularmente o eixo
y . Encontre o ponto de interseção neste caso.
b) Considere a reta x + 3y + 12 = 0 dessa família para p = 1. Denote por A o seu ponto de interseção com
o eixo x e por O a origem do plano cartesiano. Exiba a equação da circunferência em que o segmento OA
é um diâmetro.
RESOLUÇÃO:
a) A equação (2 − p)x + (2 p +1) y + 8 p + 4 = 0 pode ser representada na forma reduzida por
2−p
2−p
8p + 4
y=−
x−
onde −
é o valor que da tangente do ângulo que a reta forma com o
2p + 1
2p + 1
2p + 1
semieixo positivo Ox. Sendo a perpendicular ao eixo y, ela é paralela ao eixo x e portanto
−
2−p
=0⇒2−p =0⇒p =2 .
2p + 1
5
Poder-se-ia também desenvolver o raciocínio do seguinte modo:
Sendo a reta (2 − p)x + (2 p +1) y + 8 p + 4 = 0 perpendicular ao eixo y, ela é paralela ao eixo x e
portanto na sua forma geral o coeficiente de x é nulo, portanto 2 – p = 0 ⇒ p = 2.
RESPOSTA: 2
b) A interseção da reta x + 3y + 12 = 0 com o eixo dos x é o ponto A(x, 0), logo x = −12 e A(−12, 0).
Sendo O a origem do plano cartesiano, a medida do segmento OA é 12.
Sendo o segmento AO um diâmetro da circunferência em questão, o centro dessa circunferência é o ponto
(0, −6) e seu raio mede 6.
A equação da circunferência é x 2 + ( y + 6) 2 = 36 ⇒ x 2 + y 2 + 12 y + 36 = 36 ⇒ x 2 + y 2 + 12y = 0
RESPOSTA: x 2 + y 2 + 12y = 0
20. Numa piscina em formato de paralelepípedo, as medidas das arestas estão em progressão geométrica
de razão q >1.
a) Determine o quociente entre o perímetro da face de maior área e o perímetro da face de menor área.
b) Calcule o volume dessa piscina, considerando q = 2 e a área total do paralelepípedo igual a 252 m2 .
RESOLUÇÃO:
a) Considerando as arestas da piscina como
x
, x e qx .
q
Perímetro da face de maior área: 2x(1 + q).
 1
Perímetro da face de menor área: 2x1 +  .
 q
  1 
1+ q 
q
 = (1 + q) ×
Quociente pedido: 2x(1 + q) : 2x1 +  = (1 + q) : 
=q.
1+ q
 q 
  q 
RESPOSTA: q.
b) A área total do paralelepípedo é dada pela expressão: 2qx 2 +

2x 2
1 
+ 2x 2 = 2x 2  q + + 1 .
q
q 


1 
Fazendo 2x 2  q + + 1 = 252 e substituindo q por 2:
q 

1 
252

2x 2  2 + + 1 = 252 ⇒ x 2 (4 + 1 + 2) = 252 ⇒ x 2 =
⇒ x 2 = 36 ⇒ x = 6 .
2
7


6
Logo as arestas do paralelepípedo medem , 6 e 2 × 6 , ou seja, 3, 6 e 12.
2
O volume da piscina é 3 × 6 × 12 m3 = 216 m3.
RESPOSTA: 216 m3.
6
21. Considere o polinômio p(x) = x2 − 11x + k + 2, em que x é variável real e k um parâmetro fixo,
também real.
a) Para qual valor do parâmetro k o resto do quociente de p(x) por x − 1 é igual a 3?
π π
b) Supondo, agora, k = 4 , e sabendo que a e b são raízes de p(x) , calcule o valor de sen +  .
a b
RESOLUÇÃO:
Para que o resto do quociente de p(x) por x − 1 seja igual a 3, tem-se p(1) = 3.
Logo: 1 − 11 + k + 2 = 3 ⇒ k =11.
RESPOSTA: 11
b) Em p(x) = x2 − 11x + k + 2, substituindo k por 4, p(x) = x2 − 11x + 6. Se as raízes deste polinômio são
os valores a e b, tem-se a + b = 11 e a.b = 6.
5π 
1
π π
 π(a + b) 
 11π 

 5π 
sen +  = sen
 = sen
 = sen π +  = − sen  = − .
a
b
ab
6
6
6
2








 
RESPOSTA: −
1
.
2
 1
α
22. Considere a matriz A α = − 1 − 1 que depende do parâmetro real α > 0.
 α

a) Calcule a matriz (Aα
+A2α)2.
x 
b) Um ponto no plano cartesiano com as coordenadas   é transformado pela matriz Aα
 y
 x'
 x   x + αy 
.
em um novo ponto da seguinte forma:   = A α   =  1
 y'
 y − α x − y
 x  − 6
Calcule o valor de α, sabendo que o sistema A α   =   admite solução.
 y  2 
RESOLUÇÃO:
 1
a) a matriz A α =  1
− α
 1
A α + A2α =  1
− α
α
 que depende do parâmetro real α >
− 1

α  1
+ 1
− 1 −
  2α
0,
2α   2
= 3
− 1 −
  2α
3α 
⇒
− 2
 1


− 2 0 
RESPOSTA: 
 1

1 
0 
3α   2
3α  −
 2

0
−
2
(A α + A2α ) = − 3 − 2 × − 3 − 2 =  2 1 
2

 2α
  2α
  0 − 
2

x
+
αy = −6

α   x  − 6 
 1
 x  − 6
x + αy = −6
1
×   =   ⇒  x
b) A α   =   ⇒ 
⇒
⇒
−
−
1
 α
  y   2  − − y = 2
 y  2 
− x − αy = 2α
 α
x + αy = −6
 2α − 6 = 0
(somando as duas equações) ⇒ 

− x − αy = 2α
α = 3
RESPOSTA: α = 3.
7
23. Um recipiente cúbico de aresta a e sem tampa, apoiado em um plano horizontal, contém água até a
3
α . Inclina-se lentamente o cubo, girando-o em um ângulo θ em torno de uma das arestas da
4
base, como está representado na figura abaixo.
altura
a) Supondo que o giro é interrompido exatamente antes de a água começar a derramar, determine a
tangente do ângulo θ.
b) Considerando, agora, a inclinação tal que tg(θ) = 1/4, com 0 < θ < π/2 , calcule o valor numérico da
expressão cos(2θ) – sen(2θ).
RESOLUÇÃO:
a) Se o recipiente cúbico de aresta a contém água até a altura
3
3α 3α 3
α , o volume da água é V = α × α ×
=
.
4
4
4
Se o giro é interrompido exatamente antes de a água começar a
α3
.
4
A parte do recipiente vazio de água é um prisma de base ABC e
α 3 xα
α
α
altura α,
=
×α ⇒ = x ⇒ x = .
4
2
2
2
α
1
tgθ = : α =
2
2
derramar, o volume da parte do recipiente vazio de água é
RESPOSTA:
1
2
b) Considerando, agora, a inclinação tal que tgθ =
1
, com 0 < θ < π/2 e o
4
triângulo retângulo ABC de catetos 1(oposto a θ) e 4, BC = 1 + 16 = 17 .
17
4 17
e cosθ =
⇒
17
17
17 4 17
8
16 1 15
sen (2θ ) = 2senθsenθ = 2 ×
×
=
e cos(2θ ) = cos 2θ − sen 2θ =
−
=
17
17
17
17 17 17
15 8
7
Logo cos(2θ) – sen(2θ) =
.
−
=
17 17 17
Logo senθ =
RESPOSTA:
7
.
17
8
24. Um satélite orbita a 6.400 km da superfície da Terra. A figura abaixo representa uma seção plana que
inclui o satélite, o centro da Terra e o arco de circunferência AB . Nos pontos desse arco o sinal do
satélite pode ser captado. Responda às questões abaixo, considerando que o raio da Terra também mede
6.400 km.
a) Qual o comprimento do arco AB indicado na figura?
b) Suponha que o ponto C da figura seja tal que cos(θ) = 3/4. Determine a distância d entre o ponto C e o
satélite.
RESOLUÇÃO:
a) Analisando a figura conclui-se que cosα =
OB 6400 1
=
= ⇒
OS 12800 2
α = 60° ⇒ que o arco AB mede 120° ⇒
l
l
120°
1
12800π
=
⇒
= ⇒l =
2 × 6400π 360°
12800π 3
3
RESPOSTA:
12800π
12800 π
.
3
b) Aplicando a Lei dos Cossenos ao triângulo COS:
x 2 = r 2 + 4r 2 − 2 × r × 2r × cosθ ⇒
x 2 = 5r 2 − 4r 2 ×
3
⇒ x 2 = 2r 2 ⇒ x = r 2 ⇒
4
x = 6400 2 .
RESPOSTA: 6400 2 km
9