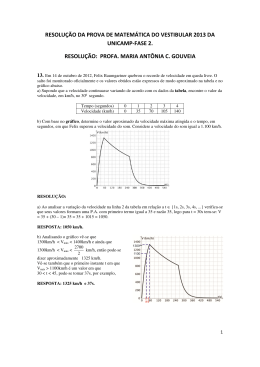
Matemática
UNICAMP
ETAPA
QUESTÃO 13
QUESTÃO 14
Em 14 de outubro de 2012, Felix Baumgartner
quebrou o recorde de velocidade em queda
livre. O salto foi monitorado oficialmente e
os valores obtidos estão expressos de modo
aproximado na tabela e no gráfico abaixo.
a) Supondo que a velocidade continuasse
variando de acordo com os dados da tabela,
encontre o valor da velocidade, em km/h,
no 30º segundo.
Os lados do triângulo ABC da figura abaixo
têm as seguintes medidas: AB = 20, BC = 15
e AC = 10.
Tempo (segundos) 0
1
Velocidade (km/h) 0
35 70 105
2
3
4
140
b) Com base no gráfico, determine o valor
aproximado da velocidade máxima atingida
e o tempo, em segundos, em que Felix superou a velocidade do som. Considere a velocidade do som igual a 1.100 km/h.
a) Sobre o lado BC marca-se um ponto D tal
que BD = 3 e traça-se o segmento DE paralelo ao lado AC. Ache a razão entre a altura
H do triângulo ABC relativa ao lado AC e a
altura h do triângulo EBD relativa ao lado
ED, sem explicitar os valores de h e H.
b) Calcule o valor explícito da altura do triângulo ABC em relação ao lado AC.
Resposta
Consideremos a figura:
Resposta
a) Com base na tabela, a função que representa a velocidade, em km/h, em função do
tempo, em segundos, deve ser linear com
V(x) = 35 ⋅ x. Portanto, V(30) = 1 050 km/h.
b) O valor da velocidade máxima, segundo o
gráfico, está entre 1 300 km/h e 1 400 km/h,
mais próximo de 1 300 km/h, então uma
boa aproximação para a velocidade máxima
é de 1 320 km/h.
O tempo que Felix demora para passar a
velocidade do som, segundo o gráfico, está
entre 30 s e 45 s, assim uma boa aproximação seria 37 s.
Unicamp
a) Como DG //CA , pelo caso AA, temos
H BF
BC 15
ΔGBD ∼ ΔFBC. Logo
=
=
=
=
h BG BD
3
= 5.
b) Seja CF = x. Como os triângulos BFC e
BFA são retângulos em F, pelo Teorema de
Pitágoras temos:
H2 + x2 = 152
2
2
H + (10 + x) = 20
( 1)
2
( 2)
De (2) − (1): (10 + x)2 − x2 = 175 + x =
Substituindo em (1): H2 +
+H=
ETAPA
2
15
.
4
152
= 152 +
16
15 15
.
4
QUESTÃO 15
A superfície de um reservatório de água
para abastecimento público tem 320.000 m2
de área, formato retangular e um dos seus
lados mede o dobro do outro. Essa superfície é representada pela região hachurada na
ilustração abaixo. De acordo com o Código
Florestal, é necessário manter ao redor do reservatório uma faixa de terra livre, denominada Área de Proteção Permanente (APP),
como ilustra a figura abaixo. Essa faixa deve
ter largura constante e igual a 100 m, medidos a partir da borda do reservatório.
a) Calcule a área da faixa de terra denominada APP nesse caso.
b) Suponha que a água do reservatório diminui de acordo com a expressão V(t) = V0 2−t,
em que V0 é o volume inicial e t é o tempo
decorrido em meses. Qual é o tempo necessário para que o volume se reduza a 10%
do volume inicial? Utilize, se necessário,
log10 2 ≈ 0,30.
Resposta
a) Sendo x e 2x as dimensões do retângulo cuja superfície tem área 320 000 m2,
temos: x ⋅ 2x = 320 000 + x = 400 m. Assim, a área da faixa de terra APP corresponde a 4 áreas de setores circulares de
medida angular 90º e raio 100 m mais duas
vezes a área de uma região retangular de
dimensões 400 m por 100 m mais duas
vezes a área da região retangular de dimensões 2 400 = 800 m por 100 m, ou seja,
1
4 $ $ 1002 π + 2 $ (100 $ 400 + 100 $ 800) =
4
=10 000(π + 24) m2.
b) Para que o volume se reduza a 10% do inicial, devemos ter V(t) = 0,1 ⋅ V0 + V0 ⋅ 2−t = 0,1 ⋅
⋅ V0 + 2 −t = 10 −1 + log 2 −t = log 10 −1 + −t ⋅
1
1
⋅ log 2 = −1 + t =
,
= 3 meses
log10 2
0, 3
e 10 dias.
QUESTÃO 16
A numeração dos calçados obedece a padrões distintos, conforme o país. No Brasil,
essa numeração varia de um em um, e vai
de 33 a 45, para adultos. Nos Estados Unidos a numeração varia de meio em meio, e
vai de 3,5 a 14 para homens e de 5 a 15,5
para mulheres.
a) Considere a tabela abaixo.
Numeração
brasileira (t)
Comprimento do
calçado (x)
35
23,8 cm
42
27,3 cm
Suponha que as grandezas estão relacionadas por funções afins t(x) = ax + b para a
numeração brasileira e x(t) = ct + d para o
comprimento do calçado. Encontre os valores dos parâmetros a e b da expressão que
permite obter a numeração dos calçados
brasileiros em termos do comprimento, ou
os valores dos parâmetros c e d da expressão
que fornece o comprimento em termos da
numeração.
Unicamp
ETAPA
3
b) A numeração dos calçados femininos nos
Estados Unidos pode ser estabelecida de
maneira aproximada pela função real f definida por f(x) = 5(x − 20)/3, em que x é o
comprimento do calçado em cm. Sabendo
que a numeração dos calçados nk forma uma
progressão aritmética de razão 0,5 e primeiro termo n1 = 5, em que nk = f(ck), com k natural, calcule o comprimento c5.
Resposta
a) Como se admite uma relação afim entre t
e x, a equação que relaciona x e t pode ser
dada por:
27, 3 − 23, 8
⋅ (t − 35) +
x − 23,8 =
42 − 35
1
+ x − 23,8 = (t − 35) + x = 0,5t + 6,3
2
Logo os valores dos parâmetros c e d são
0,5 e 6,3, respectivamente.
Também x = 0,5t + 6,3 + t = 2x − 12,6 e os valores de a e b são, respectivamente, 2 e −12,6.
b) Como n1 = 5 e a sequência (nk) é uma
1
progressão aritmética de razão
, temos
2
1
= 7. Logo, f(c5) = 7 +
n5 = 5 + (5 − 1) ⋅
2
5 $ (c5 − 20)
+
= 7 + c5 = 24,2 cm.
3
QUESTÃO 17
Na formulação de fertilizantes, os teores
percentuais dos macronutrientes N, P e K,
associados respectivamente a nitrogênio, fósforo e potássio, são representados por x, y e z.
a) Os teores de certo fertilizante satisfazem o
seguinte sistema de equações lineares:
Z
]] 3x + y − z = 0, 20
2y + z = 0, 55
[
]
z = 0, 25
\
Calcule x e y nesse caso.
b) Suponha que para outro fertilizante
valem as relações 24% ≤ x + y + z ≤ 54%,
x ≥ 10%, y ≥ 20% e z = 10%. Indique no plano
cartesiano a seguir a região de teores (x, y)
admissíveis para tal fertilizante.
Resposta
Z
Z
]]3x + y − z = 0, 20
]]3x + y = 0, 45
a) [ 2y + z = 0, 55 + [ 2y = 0, 30 +
]
]
z = 0, 25
z = 0, 25
\Z
\
]] x = 0, 10
+ [y = 0, 15 , em particular, x = 0,10 e y = 0,15.
]z = 0, 25
\
b) Repare que, como x ≥ 10% e y ≥ 20%,
x + y + z ≥ 40%.
Assim, as restrições são:
Z
]] x + y # 44%
[ x $ 10%
]y $ 20%
\
que, no gráfico, formam o conjunto de pontos acima de y = 20%, à direita de x =10% e
abaixo da reta y = −x + 44%.
Unicamp
ETAPA
4
QUESTÃO 18
O diagrama abaixo indica a distribuição
dos alunos matriculados em três cursos de
uma escola. O valor da mensalidade de cada
curso é de R$ 600,00, mas a escola oferece
descontos aos alunos que fazem mais de um
curso. Os descontos, aplicados sobre o valor
total da mensalidade, são de 20% para quem
faz dois cursos e de 30% para os matriculados em três cursos.
a) Por estratégia de marketing, suponha que
a escola decida divulgar os percentuais de
desconto, calculados sobre a mensalidade
dos cursos adicionais e não sobre o total da
mensalidade. Calcule o percentual de desconto que incide sobre a mensalidade do
segundo curso para aqueles que fazem dois
cursos e o percentual de desconto sobre o
terceiro curso para aqueles que fazem três
cursos.
b) Com base nas informações do diagrama,
encontre o número de alunos matriculados
em pelo menos dois cursos. Qual a probabilidade de um aluno, escolhido ao acaso,
estar matriculado em apenas um curso?
b) Supondo que os cursos estão representados por um triângulo, um quadrado e uma
circunferência, entre os 9 + 7 + 6 + 4 + 2 +
+ 8 = 39 matriculados, 7 + 4 + 3 + 2 = 16
estão matriculados em pelo menos dois cursos e os 39 − 16 = 23 restantes estão matriculados em apenas um curso, de modo que
23
.
a probabilidade pedida é
39
QUESTÃO 19
Considere a família de retas no plano cartesiano descrita pela equação (2 − p)x + (2p +
+ 1)y + 8p + 4 = 0, nas variáveis x e y , em que
p é um parâmetro real.
a) Determine o valor do parâmetro p para
que a reta correspondente intercepte perpendicularmente o eixo y. Encontre o ponto
de interseção neste caso.
b) Considere a reta x + 3y + 12 = 0 dessa família para p = 1. Denote por A o seu ponto
de interseção com o eixo x e por O a origem
do plano cartesiano. Exiba a equação da circunferência em que o segmento OA é um
diâmetro.
Resposta
Resposta
a) Um estudante que faz dois cursos ganha
um desconto de 20% de 2 ⋅ 600 = 0,20 ⋅ 2 ⋅
240
⋅
⋅ 600 = 240 reais, que corresponde a
600
⋅100% = 40% em relação ao curso adicional,
e um estudante que faz três cursos ganha
um desconto de 30% de 3 ⋅ 600 = 0,30 ⋅ 3 ⋅
540
⋅
⋅ 600 = 540 reais, que corresponde a
600
⋅ 100% = 90% em relação ao curso adicional.
a) Para que a reta intercepte perpendicularmente o eixo y, o coeficiente em x da equação (2 − p)x + (2p + 1)y + 8p + 4 = 0 deve
ser nulo, ou seja, 2 − p = 0 + p = 2. Uma
equação dessa reta é (2 ⋅ 2 + 1)y + 8 ⋅ 2 + 4 =
= 0 + y = −4, ou seja, ela intercepta o eixo y
no ponto (0; −4).
b) O ponto A tem abscissa x tal que x + 3 ⋅
⋅ 0 + 12 = 0 + x = −12, e, como OA é um
diâmetro, M = (−6; 0), ponto médio de
OA , é o centro dessa circunferência cujo
raio mede 6. Assim, uma equação dessa
circunferência é (x + 6)2 + y2 = 62 +
+ x2 + y2 + 12x = 0.
QUESTÃO 20
Numa piscina em formato de paralelepípedo,
as medidas das arestas estão em progressão
geométrica de razão q > 1.
Unicamp
ETAPA
5
a) Determine o quociente entre o perímetro
da face de maior área e o perímetro da face
de menor área.
b) Calcule o volume dessa piscina, considerando q = 2 e a área total do paralelepípedo
igual a 252 m2 .
Resposta
a
, a e aq as dimensões da piscina.
q
a
Note que, como q > 1,
< a < aq.
q
a) A face de maior área tem dimensões a e
aq e a face de menor área tem dimensões
a
2 (a + aq)
=
a e . Logo a razão pedida é
q
a
2da + n
q
a (1 + q)
= q.
=
1
a d1 + n
q
b) A área total do paralelepípedo é
a
a
2 d $ a + a $ 2a + $ 2a n = 7a2 = 252 + a =
2
2
= 6 m, de modo que o volume da piscina é
a
⋅ a ⋅ 2a = a3 = 216 m3.
2
Sejam
QUESTÃO 21
Considere o polinômio p(x) = x2 − 11x + k + 2,
em que x é variável real e k um parâmetro
fixo, também real.
a) Para qual valor do parâmetro k o resto do
quociente de p(x) por x − 1 é igual a 3?
b) Supondo, agora, k = 4, e sabendo que
a e b são raízes de p(x), calcule o valor de
π π
sen d + n .
a b
Resposta
a) Pelo teorema do resto, devemos ter
p(1) = 3 + 12 − 11 ⋅ 1 + k + 2 = 3 + k = 11.
b) Para k = 4, temos p(x) = x2 − 11x + 6.
− 11
=
Se a e b são raízes de p, a + b = −
1
π π
6
= 11 e a ⋅ b =
= 6. Assim, sen d + n =
a b
1
π (a + b)
11π
π
= sen d
= sen d 2π − n =
n = sen
ab
6
6
π
1
= −sen = − .
6
2
QUESTÃO 22
R
V
S 1 α W
Considere a matriz Aα = S 1
W que deS− α − 1W
T
X
pende do parâmetro real α > 0.
a) Calcule a matriz (Aα + A2α)2.
b) Um ponto no plano cartesiano com as coorx
denadas > H é transformado pela matriz Aα
y
em um novo ponto da seguinte forma:
x + αy
x’
x
> H = Aα > H = >− 1 x − yH.
y’
y
α
Calcule o valor de α, sabendo que o sistema
x
−6
Aα > H = < F admite solução.
2
y
Resposta
R
V R
S 1 αW S 1
a) Temos Aα + A2α = S− 1 −1W + S − 1
S α
W S 2α
T
X T
R
V
S 2 3αW
= S − 3 −2 W , logo (Aα + A2α)2 =
S 2α
W
TR
XV R
V
S 2 3αW S 2 3αW
W$S 3
W=
= S− 3
S 2α −2 W S− 2α −2 W
X T
X
RT
S 2 $ 2 + 3α $ d − 3 n
S
2α
=S
S− 3 $ 2 − 2 $ d − 3 n
S 2α
2α
T
R
V
S− 1
0 W
S
W
=S 2
1 W.
− W
SS 0
2W
T
X
b) Temos
V
2αW
−1 WW =
X
V
2 $ 3α + 3α $ (−2)W
W
W=
3
$ 3α − 2 $ (−2) W
−
W
2α
X
x + αy
x
−6
−6
Aα < F = < F + > 1
=< F+
− x − yH
y
2
2
α
x + αy = − 6
x + αy = − 6
+ − x − αy
+
=2
x + αy = −2α
α
que tem solução se, e somente se, − 6 =
= −2α + α = 3.
Unicamp
ETAPA
6
a $ AE
1
a
= a3 + AE = .
2
4
2
Por ângulos alternos internos, temos que
t ) = 90o − θ & m (ADE
t ) = θ &tgθ =
m (EDC
a
1
AE
=
= 2 = .
2
a
a
1
π
b) Se tgθ =
e0<θ<
, existe ΔFGH,
4
2
retângulo, como a seguir:
Assim a ⋅
QUESTÃO 23
Um recipiente cúbico de aresta a e sem tampa, apoiado em um plano horizontal, con3
tém água até a altura a . Inclina-se lenta4
mente o cubo, girando-o em um ângulo θ
em torno de uma das arestas da base, como
está representado na figura abaixo.
a) Supondo que o giro é interrompido exatamente antes de a água começar a derramar,
determine a tangente do ângulo θ.
b) Considerando, agora, a inclinação tal que
tan(θ) = 1/4 , com 0 < θ < π/2 , calcule o valor numérico da expressão cos(2θ) − sen(2θ).
Resposta
Considere a figura:
a) Do enunciado, temos que o volume de
3
3 3
água é a ⋅ a ⋅ a =
a e, daí, o volume
4
4
1
vazio é a3 .
4
E, na figura, ele é representado pelo prisma
de base ΔAED.
Z
1
]senθ =
]
17 .
Por Pitágoras FH = 17 e [
]cos θ = 4
]
17
\
Logo, cos(2θ) − sen(2θ) = cos2θ − sen2θ − 2 ⋅
1
4
16
1
⋅ senθ ⋅ cosθ =
−
−2⋅
⋅
=
17
17
17
17
7
.
=
17
QUESTÃO 24
Um satélite orbita a 6.400 km da superfície da
Terra. A figura abaixo representa uma seção
plana que inclui o satélite, o centro da Terra e
o arco de circunferência AB. Nos pontos desse arco o sinal do satélite pode ser captado.
Responda às questões abaixo, considerando
que o raio da Terra também mede 6.400 km.
Unicamp
7
a) Qual o comprimento do arco AB indicado
na figura?
b) Suponha que o ponto C da figura seja tal
que cos(θ) = 3/4. Determine a distância d entre o ponto C e o satélite.
Resposta
a) Seja O o centro da Terra e S o ponto que
representa o satélite. O triângulo OBS é retângulo em B e tem hipotenusa OS = 6 400 +
+ 6 400 = 12 800 km e cateto OB = 6 400 km.
OB
6 400
1
Assim, temos cos SÔB =
=
= +
OS 12 800 2
ETAPA
+ m (SÔB) = 60º. Logo a medida angular do
arco AB é m (AÔB) = 2m (SÔB) = 2 ⋅ 60º =
= 120º e o comprimento do arco AB é
120 o
12 800π
$ 2π $ 6 400 =
km.
o
3
360
b) Aplicando a lei dos cossenos ao triângulo
OCS, temos SC2 = OC2 + OS2 − 2 ⋅ OC ⋅ OS ⋅
⋅ cos CÔS + d2 = 6 4002 + 12 8002 − 2 ⋅
3
⋅ 6 400 ⋅ 12 800 ⋅
+ d = 6 400 2 km.
4