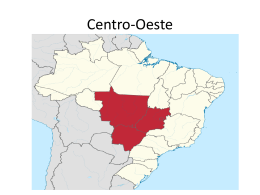
Estatística
1. (Uem 2012) Em uma área de preservação
ambiental, pesquisadores estudaram uma população
de macacos-prego. A área em questão é de 84 ha (1
2
ha = 10000 m ). Considerando o tamanho inicial da
população como 750 indivíduos (no início de 2006) e
os dados de cinco anos que estão registrados na
tabela a seguir, assinale a(s) alternativa(s) correta(s).
Determinantes
populacionais
Natalidade
Mortalidade
Imigração
Emigração
2006
200
70
7
10
2007
250
93
28
15
ANO
2008
320
57
65
32
2009
450
108
70
83
2010
510
122
48
139
01) Em condições naturais, o potencial biótico é
limitado pela resistência do meio.
02) Emigração é a entrada de novos indivíduos na
população.
04) A densidade da população, no final do ano de
2010, foi de, aproximadamente, 23,44 macacosprego/ha.
08) O tamanho da população, no final do ano de 2010,
foi de 1969 macacos-prego.
16) No final do ano de 2008, já houve um aumento de
100% da população de macacos-prego.
2. (Uem 2012) Joaquim coleciona artrópodes e, em
sua coleção, encontra-se um animal com 20 patas, um
animal com 18 patas, quatro animais com 8 patas e
oito animais com 6 patas; todos com exatamente o
número de patas mencionado e em perfeito estado.
Considerando essas informações, assinale o que for
correto.
01) A média do número de patas por animal é inferior
a 8.
02) Os animais com 20 e 18 patas podem ser
miriápodes.
04) Dentre os animais com 6 patas, podem ser
encontrados percevejos, baratas e escorpiões.
08) A mediana do número de patas em cada individuo
é 6.
16) Os animais de 8 patas podem possuir glândulas
coxais em seu sistema excretor.
a) Suponha que a partir de 2010 os índices de perdas
no varejo, no Brasil e nos EUA, possam ser
expressos por funções polinomiais do 1º grau,
y = ax + b, em que x = 0 representa o ano 2010,
x = 1, o ano 2011, e assim por diante, e y
representa o índice de perdas expresso em
porcentagem. Determine as duas funções.
b) Em que ano a diferença entre o índice de perdas no
varejo, no Brasil, e o índice de perdas no varejo,
nos EUA, será de 1%, aproximadamente? Dê como
solução os dois anos que mais se aproximam da
resposta.
5. (Fgv 2014) Um biólogo inicia o cultivo de três
populações de bactérias (A, B e C) no mesmo dia. Os
gráficos seguintes mostram a evolução do número de
bactérias ao longo dos dias.
3. (Uepg 2014) A média aritmética das notas de 20
alunos é 58. Se essas notas formam uma progressão
aritmética de razão 4, assinale o que for correto.
01) A maior nota é 96.
02) A menor nota é 20.
04) A média aritmética das cinco maiores notas é 88.
08) A mediana das notas é 52.
4. (Fgv 2014) Observe a notícia abaixo e utilize as
informações que julgar necessárias.
www.soexatas.com
Página 1
7. (Ufrgs 2014) O gráfico abaixo
mostra o registro das temperaturas
máximas e mínimas em uma cidade,
nos primeiros 21 dias do mês de
setembro de 2013.
Assinale a alternativa correta com base nos dados
apresentados no gráfico.
a) No dia 13, foi registrada a menor temperatura
mínima do período.
b) Entre os dias 3 e 7, as temperaturas máximas
foram aumentando dia a dia.
c) Entre os dias 13 e 19, as temperaturas mínimas
diminuíram dia a dia.
d) No dia 19, foi registrada a menor temperatura
máxima do período.
e) No dia 19, foi registrada a menor temperatura do
período.
A partir da informação dos gráficos, responda:
a) Em que dia o número de bactérias da população C
ultrapassou o da população A?
b) Qual foi a porcentagem de aumento da população
de bactérias B, entre o final do dia 2 e o final do dia
6?
c) Qual foi a porcentagem de aumento da população
total de bactérias (colônias A, B e C somadas) entre
o final do dia 2 e o final do dia 5?
6. (Fuvest 2014) Cada uma das cinco listas dadas é a
relação de notas obtidas por seis alunos de uma turma
em uma certa prova.
Assinale a única lista na qual a média das notas é
maior do que a mediana.
a) 5, 5, 7, 8, 9, 10
b) 4, 5, 6, 7, 8, 8
c) 4, 5, 6, 7, 8, 9
d) 5, 5, 5, 7, 7, 9
e) 5, 5, 10, 10, 10, 10
www.soexatas.com
8. (Ufg 2014) As tabelas a seguir apresentam os
casos de dengue no Brasil e na região Centro-Oeste,
no período de 1º de janeiro a 16 de fevereiro de 2013.
Casos de
dengue por
região
Casos de dengue na
região Centro-Oeste
Região
2013
Unidade
Federativa
Sudest
e
80.876
MS
Sul
12.420
MT
CentroOeste
80.976
GO
Norte
18.435
DF
Nordest
e
11.943
Brasil
204.65
0
201
3
42.0
15
10.7
65
27.3
76
820
Popul
ação
2.587.
269
3.182.
113
6.434.
048
2.789.
761
Disponível em: <www.ibge.gov.br> e <g1.globo.com/bemestar/noticia/2013/02/casos-de-dengue-nopais-190-nocomeco-de-2013-dizgoverno.html>. Acesso em: 20 out. 2013. (Adaptado).
Página 2
De acordo com essas informações,
a) Calcule a diferença entre a média dos casos de
dengue por unidade federativa da região CentroOeste e a média dos casos de dengue por unidade
federativa do Brasil no período considerado.
b) Sabendo que é considerado estado de epidemia
quando há incidência maior do que 300 casos para
cada 100 mil habitantes, determine em quais
unidades federativas da região Centro-Oeste
ocorreu estado de epidemia de casos de dengue no
período considerado.
c) E; D; B
d) B; D; C
e) A; B; D
11. (Ufg 2014) O gráfico a seguir
indica a preferência dos alunos de uma escola por
apenas uma das revistas A, B, C ou D.
9. (Ufsm 2014) O uso de biodiesel gera uma série de
efeitos ambientais, tais como a redução da emissão
de gases do efeito estufa e a diminuição da poluição
atmosférica.
O gráfico mostra a produção de biodiesel (em milhões
de litros) em uma usina, durante o período de um ano.
De acordo com os dados, a média, a mediana e a
moda (em milhões de litros) são, respectivamente,
iguais a
a) 8,5; 10 e 9.
b) 8; 9 e 10.
c) 8; 9,5 e 8.
d) 8,5; 9 e 10.
e) 8,5; 9,5 e 10.
10. (Upe 2014) Numa competição esportiva, cinco
atletas estão disputando as três primeiras colocações
da prova de salto em distância. A classificação será
pela ordem decrescente da média aritmética de
pontos obtidos por eles, após três saltos consecutivos
na prova. Em caso de empate, o critério adotado será
a ordem crescente do valor da variância. A pontuação
de cada atleta está apresentada na tabela a seguir:
Atleta
A
B
C
D
E
Pontuação 1º salto
6
7
5
4
5
Pontuação 2º salto
6
3
7
6
8
De acordo com as informações apresentadas nesse
gráfico, o número de alunos que preferem a revista D
é
a) menor que a metade dos que preferem as revistas
B ou C.
b) maior que a metade do total de alunos da escola.
c) igual à soma dos que preferem as revistas A ou B.
d) igual à média aritmética dos que preferem as
revistas A ou C.
e) dez vezes maior do que aqueles que preferem a
revista B.
12. (Enem 2014) Uma empresa de alimentos oferece
três valores diferentes de remuneração a seus
funcionários, de acordo com o grau de instrução
necessário para cada cargo. No ano de 2013, a
empresa teve uma receita de 10 milhões de reais por
mês e um gasto mensal com a folha salarial de
R$400.000,00, distribuídos de acordo com o Gráfico
1. No ano seguinte, a empresa ampliará o número de
funcionários, mantendo o mesmo valor salarial para
cada categoria. Os demais custos da empresa
permanecerão constantes de 2013 para 2014. O
número de funcionários em 2013 e 2014, por grau de
instrução, está no Gráfico 2.
Pontuação 3º salto
6
8
6
8
5
Com base nas informações apresentadas, o primeiro,
o segundo e o terceiro lugares dessa prova foram
ocupados, respectivamente, pelos atletas
a) A; C; E
b) B; D; E
www.soexatas.com
Página 3
também estiver equilibrado, então
a probabilidade de ele acertar
1
exatamente 4 questões é
.
4!
16) O número total de maneiras
possíveis de se escolher exatamente uma
alternativa de cada questão é 5!.
14. (Fgv 2014) A média mínima para um aluno ser
aprovado em certa disciplina de uma escola é 6.
A distribuição de frequências das médias dos alunos
de uma classe, nessa disciplina, é dada abaixo:
Qual deve ser o aumento na receita da empresa para
que o lucro mensal em 2014 seja o mesmo de 2013?
a) R$114.285,00
b) R$130.000,00
c) R$160.000,00
d) R$210.000,00
e) R$213.333,00
13. (Uem 2014) Quinze candidatos a uma vaga foram
submetidos a um teste seletivo que consta de 5
questões de múltipla escolha com cinco alternativas
cada (de (a) a (e)), sendo que, em cada questão, há
apenas uma alternativa correta. A pontuação de cada
candidato na prova corresponde ao número de
questões que ele acertou. Sabendo que dois
candidatos zeraram a prova, quatro candidatos
obtiveram nota 1, três candidatos obtiveram nota 2,
três candidatos obtiveram nota 3, um candidato obteve
nota 4 e dois candidatos obtiveram nota 5, assinale o
que for correto.
01) Escolhendo um candidato ao acaso, a
probabilidade de se escolher um que obteve nota
1
superior a 3 é de .
5
02) A média das notas foi 2,2.
04) A mediana das notas foi 3.
08) Se um candidato responde às 5 questões de
forma equilibrada, isto é, escolhendo alternativas
distintas para questões distintas, e se o gabarito
www.soexatas.com
A porcentagem de alunos aprovados foi:
a) 62%
b) 63%
c) 64%
d) 65%
e) 66%
15. (Ufg 2014) No quadro a seguir, estão listadas
algumas revoltas que aconteceram no Brasil e o
período em que elas ocorreram.
Revoltas
Guerra dos Mascates
Guerra dos Farrapos
Sabinada
Balaiada
Guerra de Canudos
Período
1710 - 1712
1835 - 1845
1837 - 1838
1838 - 1841
1896 - 1897
De acordo com esses dados, considerando-se o
tempo de duração dessas revoltas, a mediana desses
valores expressa uma temporalidade em que se
destaca
a) o interesse emancipacionista do movimento.
b) a ajuda estrangeira recebida pelo movimento.
c) o aspecto religioso do movimento.
d) a ênfase xenófoba do movimento.
e) o caráter republicano do movimento.
16. (Acafe 2014) Para a realização de uma olimpíada
escolar, os professores de educação física montam as
turmas por meio da distribuição das idades dos
alunos. O gráfico abaixo representa a quantidade de
alunos por suas idades.
Página 4
Considere as seguintes afirmações:
(
(
(
) Se um deles é sorteado aleatoriamente, a
probabilidade de que tenha idade abaixo da
média da turma é de 44%.
) O percentual de alunos de uma turma constituída
por alunos cuja idade é maior ou igual a 18 anos
é 56.
) A média de idade aproximada (em anos) de uma
equipe formada por alunos cuja idade é menor
ou igual a 18 anos é 17.
A sequência correta, de cima para baixo, é:
a) V - V - V
b) V - V - F
c) V - F - F
d) F - F - V
17. (Ufg 2014) Os gráficos a seguir apresentam os
dados referentes ao comércio eletrônico no Brasil em
2013.
a) Se não for considerado o consumo do Estado de
São Paulo, quantas pizzas são consumidas
diariamente no Brasil?
b) Quantas pizzas de mozarela e de calabresa são
consumidas diariamente no Estado de São Paulo?
19. (Upe 2014) Leia o trecho do artigo publicado no
Diário de Pernambuco em 21/11/2012.
A Copa do Mundo é do Nordeste - A Fifa anunciou a
distribuição geográfica do Mundial em 2014, e o
Nordeste é a região do país que mais receberá jogos.
Impulsionados pelo crescimento econômico e pelo
potencial turístico, Recife, Natal, Fortaleza e Salvador
1
da competição – incluindo dois ou três
vão sediar
3
jogos da seleção brasileira – que, no entanto, não
atuará em Pernambuco [...].
De acordo com os dados da reportagem, a distribuição
dos 64 jogos da Copa do Mundo pode ser
representada pelo gráfico abaixo:
De acordo com os dados apresentados nesses
gráficos, considerando que os produtos mais vendidos
no segundo semestre mantenham o mesmo
porcentual de vendas do primeiro semestre de 2013,
calcule o valor correspondente às vendas de produtos
eletrônicos no segundo semestre de 2013.
18. (Unicamp 2014) A pizza é, sem dúvida, o alimento
preferido de muitos paulistas. Estima-se que o
consumo diário no Brasil seja de 1,5 milhão de pizzas,
sendo o Estado de São Paulo responsável por 53%
desse consumo. O gráfico abaixo exibe a preferência
do consumidor paulista em relação aos tipos de pizza.
www.soexatas.com
Com base nas informações, analise as seguintes
afirmativas:
I. O número de jogos da região Nordeste supera o das
regiões Norte, Sul e Centro-Oeste juntas.
II. O número de jogos da região Centro-Oeste
corresponde, aproximadamente, a 6,3% do total de
jogos da Copa do Mundo.
III. A região Nordeste vai sediar, aproximadamente,
91% de jogos a mais que a região Centro-Oeste.
Página 5
Está CORRETO o que se afirma, apenas, em
a) II.
b) III.
c) I e II.
d) I e III.
e) II e III.
20. (Uneb 2014)
não é reposto, e as partes mais
moles e internas do dente logo
apodrecem. A acidez de vários
alimentos e bebidas comuns é
surpreendentemente alta; as
substâncias listadas a seguir, por exemplo, podem
causar danos aos seus dentes com contato
prolongado.
(BREWER. 2013, p. 64).
De acordo com o gráfico, a diferença entre a altura
mediana e a média das alturas desses seis jogadores,
em cm, é aproximadamente igual a
a) 0,93
b) 1,01
c) 1,09
d) 1,17
e) 1,25
21. (Ufpr 2014) O gráfico abaixo representa a
quantidade aproximada de animais adotados ao longo
de cinco anos em uma determinada cidade.
COMIDA/BEBIDA
SUCO DE LIMÃO/LIMA
CAFÉ PRETO
VINAGRE
REFRIGERANTES DE COLA
SUCO DE LARANJA
MAÇÃ
UVA
TOMATE
MAIONESE/MOLHO DE SALADA
CHÁ PRETO
PH
1,8 – 2,4
2,4 – 3,2
2,4 – 3,4
2,7
2,8 – 4,0
2,9 – 3,5
3,3 – 4,5
3,7 – 4,7
3,8 – 4,0
4,0 – 4,2
22. (Uneb 2014) Considerando-se que os valores do
pH na tabela variem unicamente com um incremento
de 0,1, pode-se afirmar que o valor modal do pH,
nessa tabela, é igual a
a) 3,2
b) 3,4
c) 3,6
d) 3,8
e) 4,0
23. (Fgv 2013) O gráfico de barras indica como
informação principal o número de pessoas atendidas
em um pronto-socorro, por faixa etária, em um
determinado dia. Outra informação apresentada no
gráfico, por meio das linhas verticais, é a frequência
acumulada. Em virtude de um rasgo na folha em que o
gráfico estava desenhado, as informações referentes
à última barra, e apenas elas, foram perdidas, como
se vê na figura.
Qual foi a média anual de animais adotados, ao longo
dos cinco anos nessa cidade?
a) 350.
b) 380.
c) 390.
d) 410.
e) 440.
TEXTO PARA A PRÓXIMA QUESTÃO:
DANOS DE ALIMENTOS ÁCIDOS
O esmalte dos dentes dissolve-se prontamente em
contato com substâncias cujo pH (medida da acidez)
seja menor do que 5,5. Uma vez dissolvido, o esmalte
www.soexatas.com
A média de idade do total de pessoas de 0 a 20 anos
que frequentou o pronto-socorro nesse dia foi 12,4
anos. Nessas condições, na folha intacta do gráfico
original, o comprimento da linha vertical posicionada
Página 6
na última barra, que indica a frequência acumulada
até 20 anos de idade, em centímetros, era igual a
a) 8,8.
b) 9,6.
c) 10,4.
d) 11,2.
e) 12,0.
d) taxa de variação de preço no
estado do Pará foi de,
aproximadamente, –15%.
e) maior preço pago em julho/2012
foi no estado do Amapá.
24. (Enem 2013) Foi realizado um levantamento nos
200 hotéis de uma cidade, no qual foram anotados os
valores, em reais, das diárias para um quarto padrão
de casal e a quantidade de hotéis para cada valor da
diária. Os valores das diárias foram: A = R$200,00; B
= R$300,00; C = R$400,00 e D = R$600,00. No
gráfico, as áreas representam as quantidades de
hotéis pesquisados, em porcentagem, para cada valor
da diária.
O valor mediano da diária, em reais, para o quarto
padrão de casal nessa cidade, é
a) 300,00.
b) 345,00.
c) 350,00.
d) 375,00.
e) 400,00.
25. (Ufpa 2013) A tabela abaixo apresenta os preços
pagos ao produtor de açaí, por quilograma da fruta,
nos meses de julho/2011 e julho/2012 em estados da
região Norte.
Estados
Acre (AC)
Amapá (AP)
Amazonas
(AM)
Maranhão
(MA)
Pará (PA)
Rondônia
(RO)
Unidade
kg
kg
Julho/2011
0,75
1,30
Julho/2012
1,00
1,49
kg
0,98
0,94
kg
1,21
1,37
kg
2,16
1,69
kg
0,65
1,25
Sobre a variação de preço, considerando-se a tabela,
é correto afirmar que o(a)
a) maior variação de preço ocorreu no estado do Acre.
b) maior decrescimento de preço ocorreu no estado do
Amazonas.
c) taxa de variação de preço no estado do Maranhão
foi de, aproximadamente, 13%.
www.soexatas.com
Página 7
Resolução das Questões
Resposta da questão 1:
01 + 04 + 08 = 13.
(01) Verdadeiro.
x + x + 4 + K + x1 + 76
 x + x + 76 
x= 1 1
⇔ 1 1
 ⋅ 20 = 58 ⋅ 20
20

2

⇔ x1 + 38 = 58
(02) Falso. Emigração é a saída de indivíduos de uma
população.
(04) Verdadeiro.
Densidade da população =
Natalidade − Mortalidade + Imigração − Emigração
≅ 23,44
área em questão
⇔ x1 = 20.
[01] Correto. A maior nota é x1 + 76 = 20 + 76 = 96.
[02] Correto. A menor nota é x1 = 20.
(08) Verdadeiro.
População Total ⇒ ∑ natalidades − ∑ mortalidades + ∑ imigração − ∑ emigração = 1969
(16) Falso.
População (2008) ⇒ ∑ natalidades − ∑ mortalidades + ∑ imigração − ∑ emigração = 1343
o que implica num aumento de aproximadamente
80% em relação a quantidade inicial
Resposta da questão 2:
02 + 08 + 16 = 26.
(01) Falso.
Média de patas = x =
1× 20 + 1× 18 + 4 × 8 + 8 × 6 118
=
≅ 8,4
14
14
(02) Verdadeiro.
(04) Falso. Os escorpiões são aracnídeos e possuem
oito patas locomotoras.
(08) Verdadeiro.
Número de animais x patas –
(6,6,6,6,6,6,6,6,4,4,4,4,18,20)
Mediana é neste caso a média do número de
patas dos termos centrais, logo:
6+6
Mediana =
=6
2
[04] Correto. A média aritmética das cinco maiores
notas é
80 + 84 + 88 + 82 + 96
= 88.
5
[08] Incorreto. A mediana das notas é igual a
x10 + x11 x1 + 36 + x1 + 40
=
2
2
= x1 + 38
= 20 + 38
= 58.
Resposta da questão 4:
a) Seja f :  + →  , a função que associa a cada
ano x o índice de perdas y, no Brasil, expresso em
porcentagem. Tem-se que a taxa de variação de f
é dada por
1,76 − 1,75
= 0,01.
1− 0
Logo, dado que f(0) = 1,75, vem
f(x) = 0,01⋅ x + 1,75.
(16) Verdadeiro.
Analogamente, sendo g :  + →  , a função para os
EUA, temos
Resposta da questão 3:
01 + 02 + 04 = 07.
1,4 − 1,49
= −0,09.
1− 0
As notas dos 20 alunos constituem a progressão
aritmética (x1, x1 + 4, K, x1 + 76). Logo, como x = 58,
tem-se
Portanto, como g(0) = 1,49, concluímos que
g(x) = −0,09 ⋅ x + 1,49.
b) Tem-se que
f(x) − g(x) = 1 ⇔ 0,01⋅ x + 1,75 − ( −0,09 ⋅ x + 1,49) = 1
⇔ 0,1⋅ x = 0,74
⇔ x = 7,4.
www.soexatas.com
Página 8
Assim, como 2010 + 7,4 = 2017,4, os dois anos que
mais se aproximam da resposta são 2017 e 2018.
Resposta da questão 5:
a) O número de bactérias da população C cresce
com o tempo. Logo, do gráfico sabemos que a
população C de bactérias atingiu 103 = 1.000
indivíduos, superando, portanto, a população A no
quarto dia, com exatamente 10 4 = 10.000
indivíduos.
b) A variação percentual pedida é dada por
210 − 26
26
⋅ 100% = 1500%.
c) O resultado é igual a
2500 + 29 + 105 − (1200 + 26 + 102 )
1200 + 26 + 102
103012 − 1364
1364
≅ 7452,20%.
⋅ 100% =
Resposta da questão 6:
[D]
Na alternativa [A] tem-se
x1 =
5 + 5 + 7 + 8 + 9 + 10
7+8
≅ 7,3 < 7,5 =
= Md ;
1
6
2
na alternativa [B],
x2 =
4+5+6+7+8+8
6+7
≅ 6,3 < 6,5 =
= Md ;
2
6
2
na alternativa [C],
x3 =
4+5+6+7+8+9
6+7
= 6,5 =
= Md .
3
6
2
na alternativa [D],
x4 =
5+5+5+7+7+9
5+7
≅ 6,3 > 6 =
= Md ;
4
6
2
e na alternativa [E],
x5 =
5 + 5 + 10 + 10 + 10 + 10
10 + 10
≅ 8,3 < 10 =
= Md .
5
6
2
No dia 19, foi registrada a menor temperatura do
período.
Resposta da questão 8:
a) A média dos casos de dengue por unidade
federativa da região Centro-Oeste foi
80976
= 20244, enquanto que a média do Brasil foi
4
204650
igual a
≅ 7580. Portanto, a diferença
27
pedida é 20244 − 7580 = 12664.
b) Terá ocorrido estado de epidemia, se a razão entre
os casos de dengue e a população for maior do que
300
= 0,003.
100000
Calculando-se a razão entre os casos de dengue e
a população de cada unidade federativa da região
Centro-Oeste, vem
42015
≅ 0,1620;
2587269
10765
≅ 0,0034;
3182113
27376
≅ 0,0043
6434048
Portanto, a única lista na qual a média das notas é
maior do que a mediana é a que aparece na
alternativa [D].
e
Resposta da questão 7:
[E]
820
≅ 0,0003.
2789761
www.soexatas.com
Página 9
Portanto, em Mato Grosso do Sul, Mato Grosso e
Goiás ocorreu estado de epidemia de casos de
dengue.
Resposta da questão 9:
[D]
Rol: 5, 5, 6, 6, 8, 8, 10, 10, 10, 10, 12, 12
2 ⋅ 5 + 2 ⋅ 6 + 2 ⋅ 8 + 4 ⋅ 10 + 2 ⋅ 12
= 8,5
12
8 + 10
Mediana =
=9
2
Média =
Resposta da questão 12:
[B]
Em 2013 a empresa gastou
0,125 ⋅ 400000 = R$ 50.000,00 com
os funcionários que possuíam ensino fundamental, e o
mesmo valor com os que tinham nível superior. Já
com os funcionários que tinham ensino médio, a
despesa foi de 0,75 ⋅ 400000 = R$ 300.000,00.
Portanto, a fim de manter o lucro, a empresa deve
aumentar a receita em
70 − 50
180 − 150
⋅ 50000 +
⋅ 60000 + 50000 = 20000 + 60000 + 50000 = R$ 130.000,00.
50
150
Moda = 10 (maior frequência)
Resposta da questão 13:
01 + 02 = 03.
Resposta da questão 10:
[A]
É fácil ver que a média aritmética dos pontos obtidos
por cada atleta é igual a 6, já que todos somaram 18
pontos e foram realizados três saltos.
Por outro lado, calculando a variância dos pontos de
cada atleta, obtemos
VarA =
VarB =
(6 − 6)2 + (6 − 6)2 + (6 − 6)2
= 0,
3
2
2
2
2
2
2
(7 − 6) + (3 − 6) + (8 − 6)
≅ 4,67,
3
RoL : 0, 0, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 5, 5
[01] Verdadeira. P = 2/15 = 1/5.
[02] Verdadeira, pois
2 ⋅ 0 + 4 ⋅1+ 3 ⋅ 2 + 3 ⋅ 3 + 4 + 2 ⋅ 5
= 2,2.
15
[04] Falsa, pois a mediana (termo central do rol) é 2.
[08] Falsa. Respondendo as questões de forma
equilibrada não é possível acertar exatamente 4
questões.
5
VarC =
(5 − 6) + (7 − 6) + (6 − 6)
≅ 0,67,
3
VarD =
(4 − 6)2 + (6 − 6)2 + (8 − 6)2
≅ 2,67
3
e
VarE =
(5 − 6)2 + (8 − 6)2 + (5 − 6)2
= 2.
3
Portanto, como VarA < VarC < VarE < VarD < VarB ,
segue-se que o primeiro, o segundo e o terceiro
lugares dessa prova foram ocupados,
respectivamente, pelos atletas A, C e E.
Resposta da questão 11:
[D]
[A] Falsa, pois 20 > (10 + 25) 2.
[B] Falsa, pois 20 < (15 + 10 + 25 + 20) 2.
[C] Falsa, pois 20 < 15 + 10.
[D] Verdadeira, pois 20 = (15 + 25) 2.
[16] Falsa. O correto é 5 .
Resposta da questão 14:
[E]
O número de alunos que obtiveram média maior do
que ou igual a 6 é igual a 15 + 9 + 6 + 3 = 33.
Portanto, como a classe possui 3 + 4 + 4 + 6 + 33 = 50
alunos, segue-se que o resultado pedido é igual a
33
⋅ 100% = 66%.
50
Resposta da questão 15:
[D]
Revoltas
Guerra dos Mascates
Guerra dos Farrapos
Sabinada
Balaiada
Guerra de Canudos
Período
1710 – 1712 (2 anos)
1835 – 1845 (10 anos)
1837 – 1838 (1 ano)
1838 – 1841 (3 anos)
1896 – 1897 (1 ano)
Em ordem crescente: 1, 1, 2, 3 e 10 e a mediana é 2:
Guerra dos Mascates. Logo, a resposta correta é [D]:
a ênfase xenófoba do movimento.
[E] Falsa, pois 20 = 2 ⋅ 10.
Resposta da questão 16:
[A]
www.soexatas.com
Página 10
A idade média da turma é dada por
16 ⋅ 6 + 17 ⋅ 5 + 18 ⋅ 4 + 19 ⋅ 3 + 20 ⋅ 5 + 21⋅ 2 452
=
6+5+4+3+5+2
25
≅ 18.
A probabilidade de que um aluno sorteado ao acaso
tenha idade abaixo da média é igual a
[III] Verdadeira. A região Nordeste
vai sediar, aproximadamente,
21 − 11
⋅ 100% ≅ 91%
11
de jogos a mais que a região Centro-Oeste.
Resposta da questão 20:
[D]
60 + 50
⋅ 100% = 44%.
250
Rol: 1,73; 1,78; 1,81; 1,82; 1,83; 1,85.
O percentual de alunos de uma turma constituída por
alunos cuja idade é maior ou igual a 18 anos é
mediana =
Média =
40 + 30 + 50 + 20
⋅ 100% = 56%.
250
1,81 + 1,82
= 1,815m = 181,5cm
2
1,73 + 1,78 + 1,81 + 1,82 + 1,83 + 1,85
= (1,80333333333....) m = (180,333333...) cm
6
Logo, a diferença pedida é: (1,16666666666...)cm
(aproximadamente 1,17cm).
A média de idade aproximada (em anos) de uma
equipe formada por alunos cuja idade é menor ou
igual a 18 anos é
Resposta da questão 21:
[D]
16 ⋅ 6 + 17 ⋅ 5 + 18 ⋅ 4 253
=
≅ 17.
6+5+4
15
300 + 400 + 400 + 450 + 500
= 410.
5
Resposta da questão 17:
Supondo que a projeção de vendas em 2013 se
concretize, e sabendo que o total vendido no primeiro
semestre de 2013 foi de R$ 12,74 bilhões, tem-se que
o total de vendas esperado no segundo semestre de
2013 é igual a 28 − 12,74 = R$ 15,26 bilhões.
Portanto, o valor correspondente às vendas de
produtos eletrônicos no segundo semestre de 2013, é
0,09 ⋅ 15,26 ≅ R$ 1,37 bilhão.
Resposta da questão 22:
[E]
Resposta da questão 18:
a) O resultado pedido é (1 − 0,53) ⋅ 1,5 ⋅ 106 = 705.000
pizzas.
b) O número de pizzas de mozarela e calabresa
consumidas diariamente no Estado de São Paulo é
igual a 0,53 ⋅ (0,35 + 0,25) ⋅ 1,5 ⋅ 106 = 477.000.
Resposta da questão 19:
[B]
[I] Falsa. De acordo com o gráfico, tem-se que
21 < 4 + 9 + 11 = 24.
[II] Falsa. O número de jogos da região Centro-Oeste
corresponde, aproximadamente, a
11
⋅ 100% ≅ 17,19%
64
O pH modal é aquele que aparece com maior
frequência na tabela, portanto 4,0, pois aparece 5
vezes.
Resposta da questão 23:
[E]
De acordo com o gráfico, obtemos a seguinte tabela.
Anos
de
idade
0 −| 4
xi
2
1
2
1
4 −| 8
6
3
18
4
1
0
2
20
6
1
4
4
56
10
1
8
k
18k
8 −| 12
12 −| 16
16 −| 20
fi
xi ⋅ fi
Fi
10 + k
∑ fi = 10 + k ∑ xi ⋅ fi = 96 + 18k
Sabendo que a média de idade é igual a 12,4, temos
do total de jogos da Copa do Mundo.
www.soexatas.com
Página 11
x=
∑ xi ⋅ fi ⇔ 96 + 18k = 12,4
10 + k
∑ fi
⇔ 18k − 12,4k = 124 − 96
⇔ k = 5.
Portanto, como a frequência acumulada na última
barra é 10 + k = 10 + 5 = 15, segue-se que o seu
comprimento é igual a 8 ⋅ 15 = 120mm = 12cm.
[D] Incorreta. A taxa de variação no
estado do Pará foi de,
aproximadamente,
1,69 − 2,16
⋅ 100% ≅ −22%.
2,16
[E] Incorreta. O maior preço pago em julho/2012 foi no
estado do Pará.
Resposta da questão 24:
[C]
De acordo com o gráfico, tem-se que 200 ⋅ 0,25 = 50
hotéis cobram diárias de R$ 200,00; 200 ⋅ 0,25 = 50
hotéis cobram diárias de R$ 300,00; 200 ⋅ 0,4 = 80
hotéis cobram diárias de R$ 400,00 e 200 ⋅ 0,1 = 20
hotéis cobram diárias de R$ 600,00.
Considere a tabela abaixo, em que xi é o valor da
diária, em reais, para um quarto padrão de casal, fi é
a frequência simples absoluta e Fi é a frequência
absoluta acumulada.
xi
fi
Fi
200
300
400
600
50
50
80
20
50
100
180
200
n=
∑ fi = 200
n 200
=
= 100, segue-se que o
2
2
valor mediano da diária é
Portanto, como EMd =
Md =
300 + 400
= R$ 350,00.
2
Resposta da questão 25:
[C]
[A] Incorreta. A variação de preço no estado do Acre
foi de | 1,00 − 0,75 | = R$ 0,25, enquanto a variação
de preço no estado do Pará foi de
| 1,69 − 2,16 | = R$ 0,47.
[B] Incorreta. A redução de preço no estado do
Amazonas foi de | 0,94 − 0,98 | = R$ = 0,04,
enquanto a redução de preço no estado do Pará
foi de R$ 0,47.
[C] Correta. A taxa de variação no estado do
Maranhão foi de, aproximadamente,
1,37 − 1,21
⋅ 100% ≅ 13%.
1,21
www.soexatas.com
Página 12