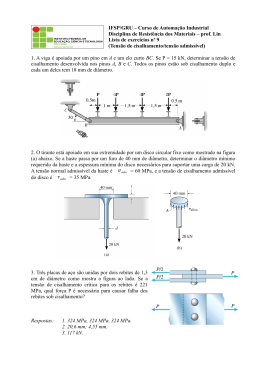
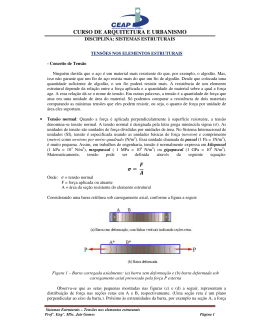
Universidade Estadual de Londrina
Estruturas
Resistência dos Materiais
01
TENSÕES
BARRA SOB CARGA AXIAL
COMPRESSÃO
FORÇA POR
UNIDADE
DE ÁREA
ESFORÇO
INTERNO
P
P
N=P
P
A
A
S’
S’
TENSÃO
P
P
P
EQUILÍBRIO
EQUILÍBRIO
σ=
P
A
(sigma)
CONCEITO DE TENSÃO
P1
P2
P3
Σ Fr
PARTE
EM
EQUILÍBRIO
CORPO
EM
EQUILÍBRIO
R2
R1
Σ Fr
FORÇAS RESISTENTES DA SEÇÃO
TENSÃO MÉDIA
P2
TENSÃO EM UM PONTO
P1
P2
P1
ΔA
t
ΔF
ΔF
ΔA
P
ΔA
R1
R1
ΔF
T =
ΔA
ΔF
t = lim
ΔA 0 ΔA
0
Tensão normal na direção x
TIPOS DE TENSÃO
ΔFx
sx = lim
ΔA 0 ΔA
Y
P1
P2
Tensão tangencial na direção y
txy
t
P
txz
txy = lim
ΔA
sx
ΔFy
0 ΔA
X
Tensão tangencial na direção z
R1
Z
txz = lim
ΔA
Tensões atuantes no plano zy, cuja normal é x
ΔFz
0 ΔA
ESTADO GERAL DE TENSÃO
Tensões atuantes no plano xy (normal z)
sz tensão normal ao plano x-y na direção z
tzy tensão tangencial ao plano x-y na direção y
tzx tensão tangencial ao plano x-y na direção x
TENSÃO NORMAL MÉDIA
DISTRIBUIÇÃO MÉDIA DE TENSÃO
HIPÓTESES
• A barra deve
permanecer reta
e a seção plana
• A carga deve
ser centroidal e o
material homogêneo
e isotrópico
TENSÃO NORMAL UNIFORME
Na seção de área A
constante
f
dF = f σ dA
P=σA
σ=
P
A
A = área da seção transversal
σ = tensão normal média em qualquer ponto de A
P = resultante da força normal aplicada no centróide de A
EQUILÍBRIO
Σ FZ = 0
σ(ΔA) – σ’(ΔA) = 0
σ = σ’
Estado uniaxial de tensões
TENSÃO NORMAL MÉDIA MÁXIMA
σ=
P
2A
A
P
A
P
3P
Diagrama de Esforços Normais
3P
P
2P
-
P
Esforço
Área
Valores de σ = P/A
P/A
3P
P
2A
A
(1,5)P/A
(1)P/A
TENSÃO MÁXIMA
TENSÃO DE CISALHAMENTO MÉDIA
F
Tangente à
superfície
resistente
Força aplicada
Tensões
tangenciais ou
de cisalhamento
seção resistente
A
F
A
C
B
F
V
V
P
Elemento estrutural
F
med = tensão de cisalhamento média na seção
V = resultante interna da força de cisalhamento
A = área da seção transversal resistente.
V
med =
A
(tau)
tmed
CISALHAMENTO SIMPLES
METAL
MADEIRA
SEÇÃO
SIMPLESMENTE
CISALHADA
JUNTA SOBREPOSTA
FINOS
• ELEMENTOS DA JUNTA
APROXIMAÇÕES
Despreza-se o momento fletor criado pela força F
• PORCA DO PARAFUSO DE LIGAÇÃO
NÃO MUITO APERTADA
Despreza-se o atrito entre os elementos
FORÇA ATUANTE
V=F
med =
V
A
CISALHAMENTO DUPLO
METAL
MADEIRA
SEÇÃO
DUPLAMENTE
CISALHADA
JUNTAS DE DUPLA SOBREPOSIÇÃO
FINOS
• ELEMENTOS DA JUNTA
APROXIMAÇÕES
Despreza-se o momento fletor criado pela força F
• PORCA DO PARAFUSO DE LIGAÇÃO
NÃO MUITO APERTADA
Despreza-se o atrito entre os elementos
FORÇA ATUANTE
V=F/2
med =
V
A
EQUILÍBRIO
ESTADO
DE
TENSÕES
CONSIDERANDO :
Σ Fy = 0
Σ Fz = 0
Σ Mx = 0
ENTÃO:
tensão x área = força
zy = ’zy
zy(ΔxΔy) - ’zy(ΔxΔy) = 0
Momento=(tensãoxárea=
de maneira similar:força)xbraço
-zy(ΔxΔy)Δz + yz(ΔxΔz)Δy = 0
zy = ’zy = yz = ’yz = 
yz = ’yz
zy = yz
CISALHAMENTO PURO
TENSÃO ADMISSÍVEL

σ
σadm
SEM
RUPTURA
adm
TENSÃO
ADMISSÍVEL
<
MÁXIMA TENSÃO NO MATERIAL
TENSÃO QUE O
MATERIAL PODE
SUPORTAR
SEM
DEFORMAÇÕES
EXAGERADAS
JUSTIFICATIVAS
• Carga de projeto diferente da carga aplicada
MÉTODO
ULTRAPASSADO
• Carga acidentais não consideradas no projeto
• Corrosão e desgaste dos materiais
• Variação das propriedades dos materiais
PARÂMETRO DE
DIMENSIONAMENTO
E VERIFICAÇÃO
PROJETO DE ACOPLAMENTO SIMPLES
BARRA TRACIONADA
A
A==
P
σadm
PROJETO DE ACOPLAMENTO SIMPLES
LIGAÇÕES SIMPLES
A=
P
adm