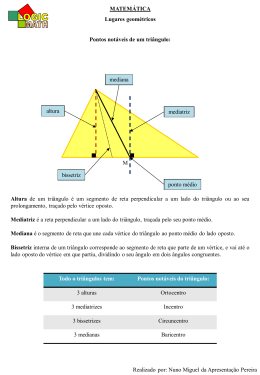
Triângulos
Prof. Ilizete
1) CONDIÇÃO DE EXISTÊNCIA
Em todo triângulo, qualquer lado é menor que a soma e maior que
a diferença entre os outros dois.
b
c
a
b - c  a  b + c
2) ELEMENTOS
Altura: é o segmento de reta que liga um vértice ao lado oposto,
perpendicularmente.
Bissetriz interna: é a semi-reta que divide o ângulo em dois ângulos de
medidas iguais.
2) ELEMENTOS
Observação: Teorema da Bissetriz Interna.
A bissetriz interna de um triângulo determina sobre o lado oposto dois
segmentos proporcionais aos outros dois lados.
A
B
P
C
AB AC

BP PC
2) ELEMENTOS
Mediana: é o segmento de reta que liga um vértice ao ponto médio do
lado oposto.
Mediatriz: é a reta perpendicular a um lado, que o divide em dois
segmentos de mesma medida.
2) ELEMENTOS
Baricentro: é o ponto de interseção das medianas.
OBSERVAÇÃO: O baricentro divide cada mediana na razão 2/3 a partir
do vértice.
2) ELEMENTOS
Incentro: é o ponto de interseção das bissetrizes.
OBSERVAÇÃO: O incentro é o centro da circunferência inscrita no
triângulo. Assim, o incentro é eqüidistante dos lados do triângulo.
2) ELEMENTOS
Circuncentro: é o ponto de interseção das mediatrizes.
OBSERVAÇÃO: O circuncentro é o centro da circunferência circunscrita
ao triângulo. Assim o circuncentro é equidistante dos vértices do
triângulo.
2) ELEMENTOS
Ortocentro: é o ponto de interseção das alturas.
2) ELEMENTOS
OBSERVAÇÃO: Os pontos de interseções, baricentro, circuncentro e
ortocentro, de uma maneira geral são pontos distintos. Mas em
qualquer triângulo, eles estão alinhados (Reta de Euler)
Se o triângulo for eqüilátero, os quatro pontos (baricentro, incentro,
ortocentro e circuncentro) são coincidentes.
3) SEMELHANÇA DE TRIÂNGULOS
Dois triângulos são semelhantes quando possuem lados homólogos*
proporcionais e ângulos respectivamente de mesmas medidas.
*
lados homólogos: são lados opostos a ângulos iguais.
3) SEMELHANÇA DE TRIÂNGULOS
3 cm
2 cm
45o
60o 45o
50o 3 cm
60o
4 cm
2 cm
8 cm
3 cm
4 cm
50o
6 cm
4,5 cm
4) RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
A
b
C
b2 = a.m
c
h
m
n
a
h2 = m.n
B
a.h = b.c
a2 = b 2 + c 2
c2 = a.n
Questão 1:
(UCSal/adaptada) Na figura abaixo têm-se o triângulo ABC, cujo
perímetro é 26cm e o losango ADEF, cujos lados medem 4cm. Se BC
mede 8cm e sendo AB paralelo à EF, os outros dois lados do
triângulo ABC medem:
a)
b)
c)
d)
e)
5 e 13
6 e 12
7 e 11
8 e 10
9e9
Questão 2:
(Fuvest) Num triângulo ABC, os ângulos B e C medem
50° e 70°, respectivamente. A bissetriz relativa ao
vértice A forma com a reta BC ângulos proporcionais
a:
a) 1 e 2
b) 2 e 3
c) 3 e 4
d) 4 e 5
e) 5 e 6
Questão 3:
Dois navios partem de um mesmo ponto
com velocidades iguais a VA= 15Km/h às 14
horas e VB= 60Km/h às 20 horas,
formando entre si dimensões cujo ângulo é
de 60°. Qual a distância que separa os
navios às 22 horas do mesmo dia?
Questão 4:
(UFRJ) Os pontos médios dos
lados de um quadrado de perímetro
2x são vértices de um quadrado de
perímetro:
Questão 5:
(Unicamp) Uma rampa de inclinação constante, como a que dá
acesso ao Palácio do Planalto em Brasília, tem 4 metros de altura
na sua parte mais alta. Uma pessoa, tendo começado a subi-la, nota
que, após caminhar 12,3 metros sobre a rampa, está a 1,5 metros
de altura em relação ao solo.
a) Faça uma figura ilustrativa da situação descrita.
b) Calcule quantos metros a pessoa ainda deve caminhar para
atingir o ponto mais alto da rampa.